初识JAVA中的包装类,时间复杂度及空间复杂度

public class Test {public static void main(String[] args) {/*** 装箱*/int a = 2;a = Integer.valueOf(a);//手动 or 显示装箱Integer b = 1;//(自动)隐式装箱,实则调用了Integer.valueOf方法System.out.println(a);System.out.println(b);// Integer c = 10;/*** 拆箱*//*int a = c.intValue(); //手动拆箱System.out.println(a);int d = c;System.out.println(d);//自动拆箱*/}
}自动拆(装)箱可以用,反汇编查看(out目录指令:javap -c),其实也是调用了,手动拆(装)箱的方法。

补充:
二.时间复杂度:
1.算法的时间复杂度是一个数学函数,,算法中的基本操作的执行次数,为算法的时间复杂度
2.大O的渐进表示法:我们表示时间复杂度哈空间复杂度,都是通过这个公式。(实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数)
3.例子:这里第一个循环,执行了2n次,第二个循环,执行了10次,共2n+10,根据大O渐进法,时间复杂度为:O(n)。
void func2(int N) {
int count = 0;
for (int k = 0; k < 2 * N ; k++) {
count++;
}
int M = 10;
while ((M--) > 0) {
count++;
}
System.out.println(count);
}计算时间复杂度,要根据,具体算法代码来,考量。比如下面的二分查找:
这个是按照,一半一半来查找,设找了X次找到,一个数字。格式为:2^1/1 , 2^2/1........一直到
2^x/1 ==(1)找到的数字。X==log2,所以时间复杂度就是为,log2
int binarySearch(int[] array, int value) {
int begin = 0;
int end = array.length - 1;
while (begin <= end) {
int mid = begin + ((end-begin) / 2);
if (array[mid] < value)
begin = mid + 1;
else if (array[mid] > value)
end = mid - 1;
else
return mid;
}
return -1;
}三.空间复杂度:
void bubbleSort(int[] array) {
for (int end = array.length; end > 0; end--) {
boolean sorted = true;
for (int i = 1; i < end; i++) {
if (array[i - 1] > array[i]) {
Swap(array, i - 1, i);
sorted = false;
}
}
if (sorted == true) {
break;
}这里有一题典型的例子:求下面空间复杂度?
public static int[][] get2Array(int n){int[][] array = new int[n][];for(int i = 0; i < n; i++) {array[i] = new int[n-i];n--;}return array;
}这里应该是:刚开始有N个,空间,然后有每次开辟,比之前少的一块空间。

空间总的个数为:1+2+3+...+N-1 + N + N = (1+N)*N/2 + N = N^2/2 + 3N/2
这里空间复杂度就为O(N^2)
相关文章:

初识JAVA中的包装类,时间复杂度及空间复杂度
目录: 一.包装类 二.时间复杂度 三.空间复杂度 一.包装类: 在Java中,由于基本类型不是继承自Object,为了在泛型代码中可以支持基本类型,Java 给每个基本类型都对应了一个包装类型。 1 基本数据类型和对应的包装类 &am…...

RapidMiner如何利用Hugging Face中的模型实现更有趣的事
RapidMiner Studio最新发布的功能更新,重点是嵌入Hugging Face和Open AI,Hugging face中含有大量的可用模型,包含翻译、总结、文本生成等等强大的模型,Open AI更不必说了,生成界的鼻祖。那么今天主要介绍一下RapidMine…...

Vue3 自定义Hooks函数的封装
1、如何理解vue3中的自定义hooks 在Vue 3中,自定义hooks允许开发者封装和重用逻辑代码。自定义hooks是使用Composition API时创建的函数,这些函数可以包含任意的组合逻辑,并且可以在多个组件之间共享。 自定义hooks通常遵循这样的命名约定&…...

python的DataFrame和Series
Series、DataFrame 创建 pd.Series() pd.DataFrame() # 字典{列名:[值1,值2],} [[]] [()] numpy Pandas的底层的数据结构,就是numpy的数组 ndarray 常用属性 shape (行数,) (行数,列数) values → ndarray index 索引名 siz…...
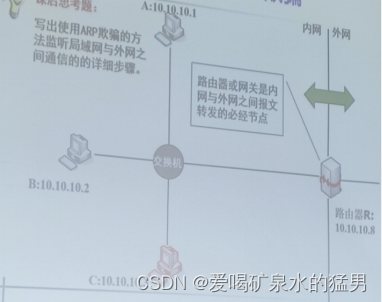
ARP欺骗的原理与详细步骤
ARP是什么: 我还记得在计算机网络课程当中,学过ARP协议,ARP是地址转换协议,是链路层的协议,是硬件与上层之间的接口,同时对上层提供服务。在局域网中主机与主机之间不能直接通过IP地址进行通信,…...

25、DHCP FTP
DHCP 动态主机配置协议 DHCP定义: 服务器配置好了地址池 192.168.233.10 192.168.233.20 客户端从地址池当中随机获取一个ip地址,ip地址会发生变化,使用服务端提供的ip地址,时间限制,重启之后也会更换。 DHCP优点&a…...

spark学习记录-spark基础概念
背景需求 公司有项目需要将大容量数据进行迁移,经过讨论,采用spark框架进行同步、转换、解析、入库。故此,这里学习spark的一些基本的概念知识。 Apache Spark 是一个开源的大数据处理框架,可以用于高效地处理和分析大规模的数据…...

BGP数据包+工作过程
BGP数据包 基于 TCP的179端口工作;故BGP协议中所有的数据包均需要在tcp 会话建立后; 基于TCP的会话来进行传输及可靠性的保障; 首先通过TCP的三次握手来寻找到邻居; Open 仅负责邻居关系的建立,正常进收发一次即可;携带route-id; Keepli…...
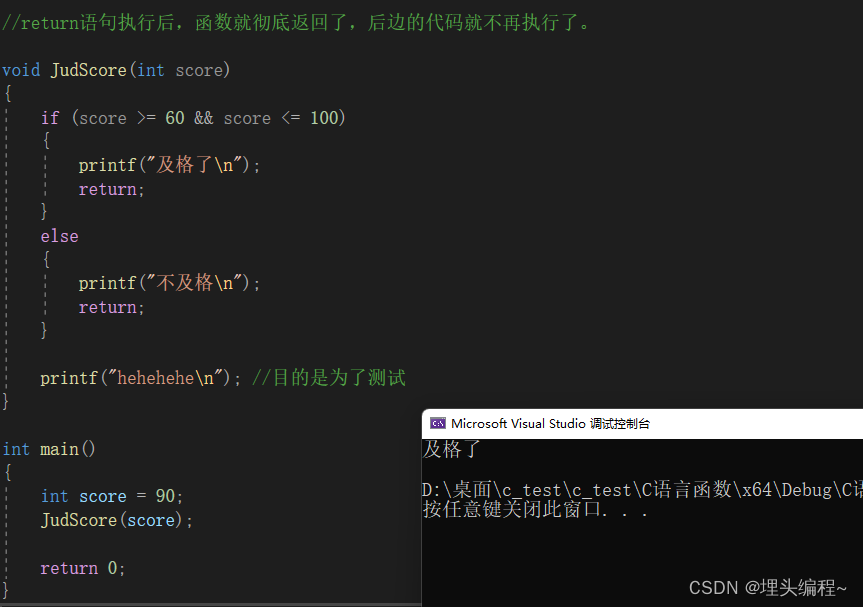
【C语言】详解函数(庖丁解牛版)
文章目录 1. 前言2. 函数的概念3.库函数3.1 标准库和头文件3.2 库函数的使用3.2.1 头文件的包含3.2.2 实践 4. 自定义函数4.1 自定义函数的语法形式4.2 函数的举例 5. 形参和实参5.1 实参5.2 形参5.3 实参和形参的关系 6. return 语句6. 总结 1. 前言 一讲到函数这块ÿ…...

createAsyncThunk完整用法介绍
createAsyncThunk 是 Redux Toolkit 库中的一个功能,它用于创建处理异步逻辑的 thunk action creator。Redux Toolkit 是一个官方推荐的库,用于简化 Redux 开发过程,特别是处理常见的 Redux 模式,如异步数据流。createAsyncThunk …...
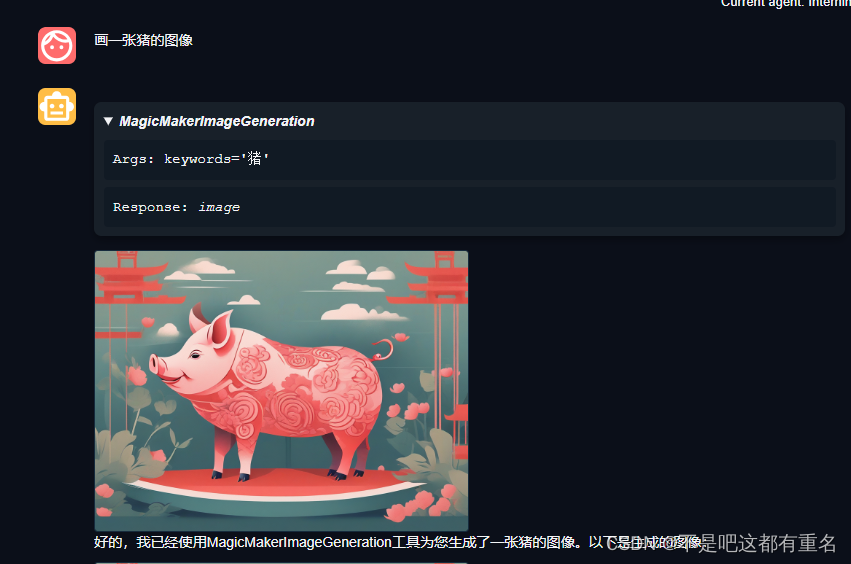
[书生·浦语大模型实战营]——第六节 Lagent AgentLego 智能体应用搭建
1. 概述和前期准备 1.1 Lagent是什么 Lagent 是一个轻量级开源智能体框架,旨在让用户可以高效地构建基于大语言模型的智能体。同时它也提供了一些典型工具以增强大语言模型的能力。 Lagent 目前已经支持了包括 AutoGPT、ReAct 等在内的多个经典智能体范式&#x…...
Word文档如何设置限制编辑和解除限制编辑操作
Word文档是大家经常使用的一款办公软件,但是有些文件内容可能需要进行加密保护,不过大家可能也不需要对word文件设置打开密码。只是需要限制一下编辑操作就可以了。今天和大家分享,如何对word文件设置编辑限制、以及如何取消word文档的编辑限…...
IO进程线程(六)进程
文章目录 一、进程状态(二)进程状态切换实例1. 实例1 二、进程的创建(一)原理(二)fork函数--创建进程1. 定义2. 不关注返回值3. 关注返回值 (三) 父子进程的执行顺序(四&…...

机器视觉——找到物块中心点
首先先介绍一下我用的是HALCON中的HDevelop软件。 大家下载好软件后可以测试一下: 在程序编辑器窗口中输入下面指令: read_image(Image,monkey) 那么如果出现这样的图片,说明是没有问题的 那么本次编程采用的是下面这张图片 我们要达到的…...

重磅消息! Stable Diffusion 3将于6月12日开源 2B 版本的模型,文中附候补注册链接。
在OpenAI发布Sora后,Stability AI也发布了其最新的模型Stabled Diffusion3, 之前的文章中已经和大家介绍过,感兴趣的小伙伴可以点击以下链接阅读。Sora是音视频方向,Stabled Diffusion3是图像生成方向,那么两者没有必然的联系&…...

Python报错:AttributeError: <unknown>.DeliveryStore 获取Outlook邮箱时报错
目录 报错提示: 现象描述 代码解释: 原因分析: 报错提示: in get_outlook_email return account.DeliveryStore.DisplayName line 106, in <module> email_address get_outlook_email() 现象描述 获取outlook本地邮箱…...
如何 Logrus IT 的质量评估门户帮助提升在线商店前端(案例研究)
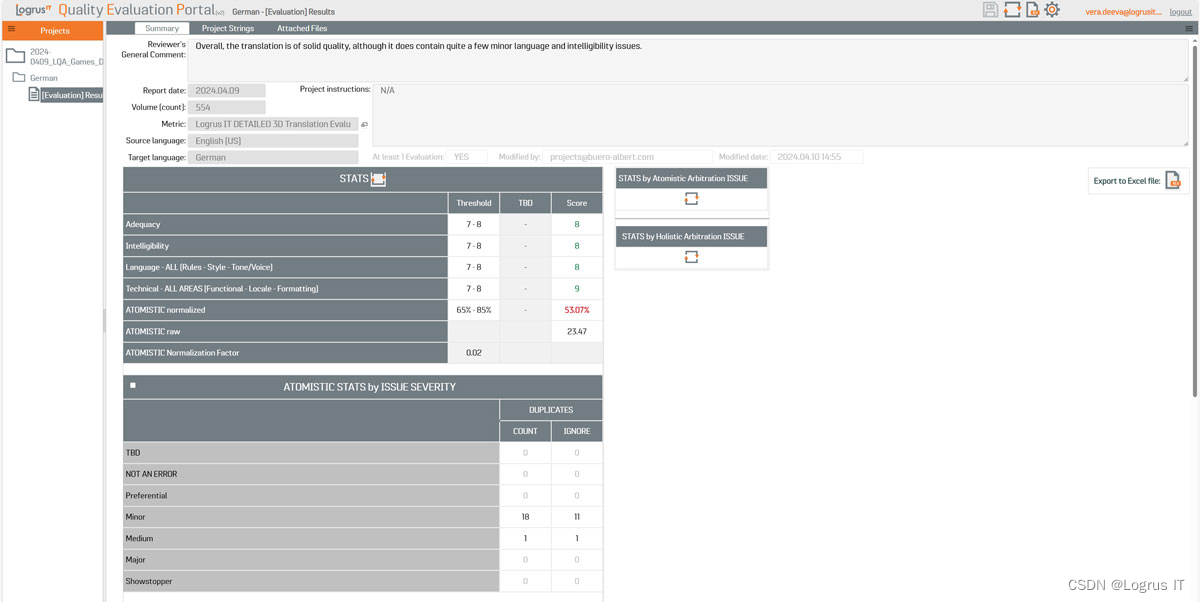
在当今竞争激烈的电子商务环境中,一个运作良好的在线店面对商业成功至关重要。然而,确保目标受众获得积极的用户体验可能是一项挑战,尤其是在使用多种语言和平台时。Logrus IT的质量评估门户是一个强大的工具,可帮助企业简化内容和…...

程序调试
自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 在程序开发过程中,免不了会出现一些错误,有语法方面的,也有逻辑方面的。对于语法方面的比较好检测,因…...
深度学习-07-反向传播的自动化
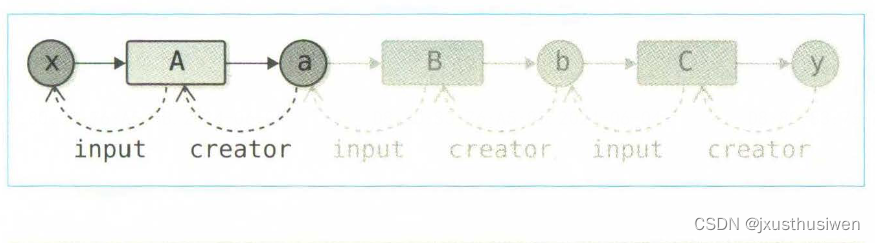
深度学习-07-反向传播的自动化 本文是《深度学习入门2-自製框架》 的学习笔记,记录自己学习心得,以及对重点知识的理解。如果内容对你有帮助,请支持正版,去购买正版书籍,支持正版书籍不仅是尊重作者的辛勤劳动…...

四川景源畅信:抖音做直播有哪些人气品类?
随着互联网科技的飞速发展,抖音作为新兴的社交媒体平台,已经成为了人们日常生活中不可或缺的一部分。而在抖音平台上,直播功能更是吸引了大量的用户和观众。那么,在抖音上做直播有哪些人气品类呢?接下来,就让我们一起…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...
