当前位置： 首页 > news >正文

期望20K，2年golang深圳某互联网小公司一面

news 2026/2/11 4:41:06

后续约了二面（CTO面），需要到现场，基本没问啥具体的技术知识，都是聊规划和个人职业目标


一面

1、假设访问百度网站，从在浏览器输入网址，到最终页面展示出来，中间会发生哪些事情？

2、http和https的区别？https如果只采用单种加密方式，例如只采用非对称加密，或对称加密，会存在什么样的问题？如果缺少CA数字证书的验证，https协议可能存在什么问题？

3、TCP 3次握手流程？握手过程中，客户端和服务端会经历哪些状态？如果没有第三次握手，这样的连接为什么就不可靠了？

4、做一道SQL题，基于你的SQL语句，你会怎样去给两张表设计索引？假设这两张表的数据量在10w以上，结合你刚才设计的索引，分析一下这个SQL查询的性能，是比较好还是比较差？

5、一般你会怎样分析一条SQL语句的性能呢？或者怎样判断一条SQL语句是好还是不好的？针对这个语句，你能大概想象它的执行计划会是怎样吗？

6、分析一下你写的语句会命中哪些索引？在explain的结果中，你提到会关注扫描行数，那针对这条语句，你觉得它的扫描行数会是多少呢

7、说一下在innoDB存储引擎下，索引是如何实现的？

8、说一下B+树有哪些特点？

9、讲一下聚簇索引和非聚簇索引的区别？

“面经哥”已累计3000+条真实面试经验，期待你的加入~

85fc8f3cec7155e8cef3c5752515d100.jpeg

相关文章：

期望20K，2年golang深圳某互联网小公司一面

后续约了二面（CTO面），需要到现场，基本没问啥具体的技术知识，都是聊规划和个人职业目标 一面 1、假设访问百度网站，从在浏览器输入网址，到最终页面展示出来，中间会发生哪些事情&…...

编程日记 2024/6/5 11:03:46

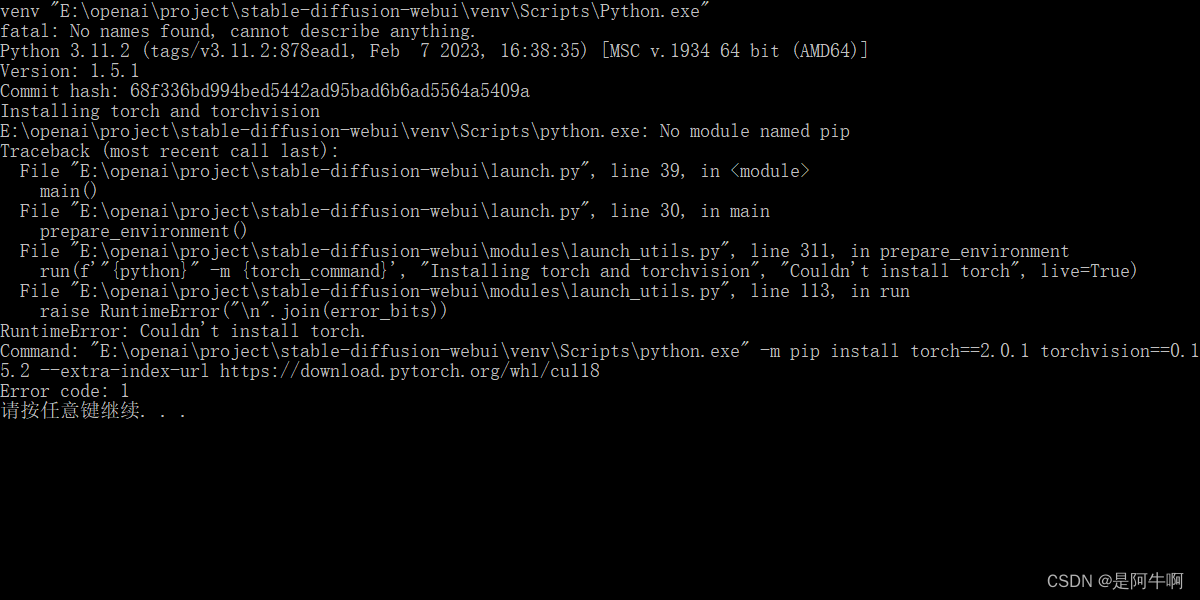
#02 安装指南：如何配置Stable Diffusion环境

文章目录 前言前置条件第1步：安装Python和PIP第2步：创建虚拟环境第3步：安装PyTorch和CUDA第4步：安装Stable Diffusion相关库第5步：测试环境结论 前言 在之前的文章中，我们介绍了Stable Diffusion基础入门和…...

编程日记 2024/6/5 11:02:45

拼多多笔试

拼多多2022数据分析笔试（0822） 一、选择题 1.已知样本量n，样本均值及方差求置信区间 2.决策树 3.峰度系数 4.协方差 5.第一、第二熵变 6.充分统计量 7.xgboost 8.方差分析中的多重比较 二、编程题 1. 一张用户点击路径的表&#x…...

编程日记 2024/6/5 11:01:42

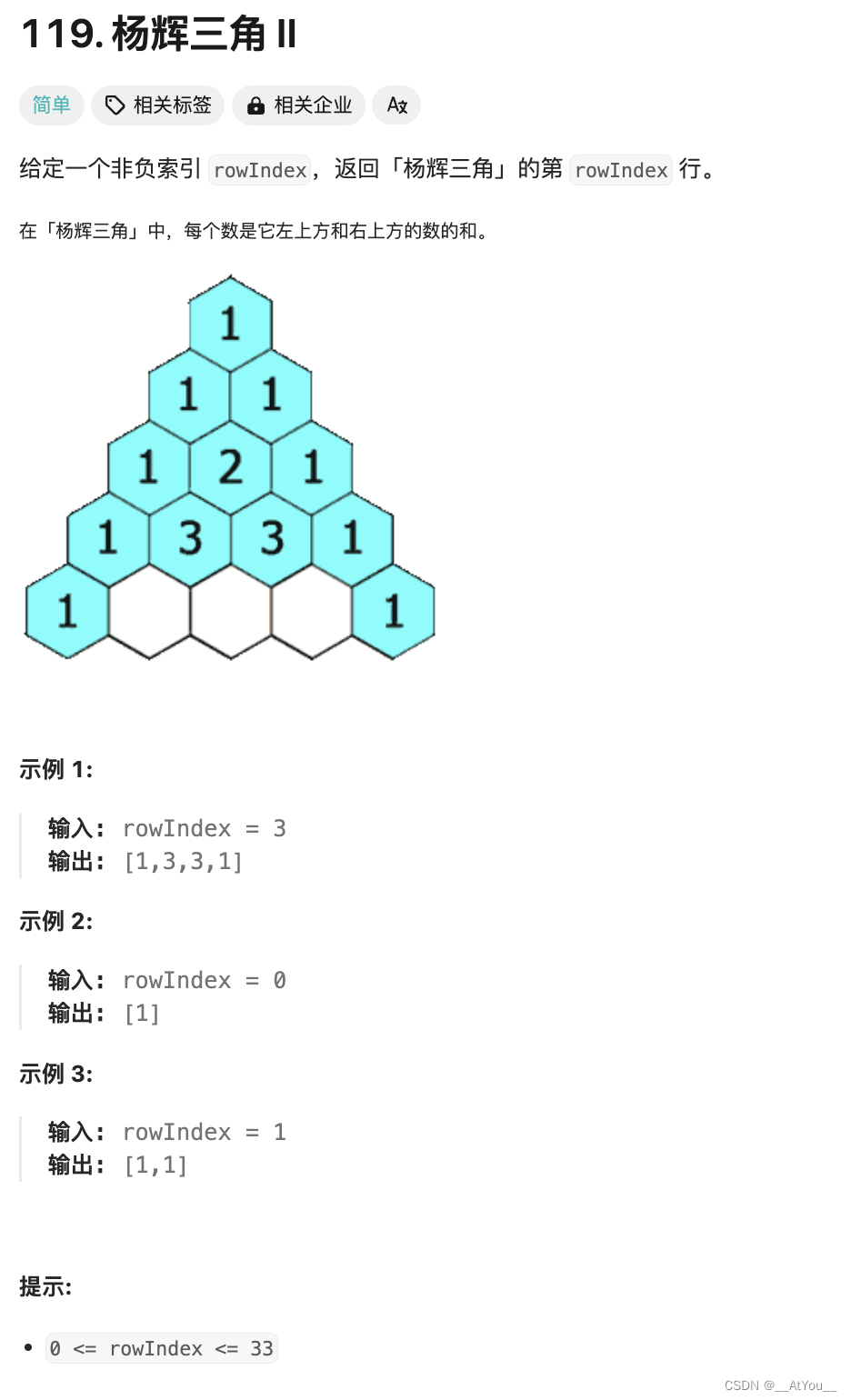
Golang | Leetcode Golang题解之第119题杨辉三角II

题目&#xff1a; 题解&#xff1a; func getRow(rowIndex int) []int {row : make([]int, rowIndex1)row[0] 1for i : 1; i < rowIndex; i {row[i] row[i-1] * (rowIndex - i 1) / i}return row }...

编程日记 2024/6/5 10:59:39

Flutter 中的 SliverIgnorePointer 小部件：全面指南

Flutter 中的 SliverIgnorePointer 小部件&#xff1a;全面指南 Flutter 是一个由 Google 开发的跨平台 UI 框架&#xff0c;它提供了一系列的组件来帮助开发者构建高性能、美观的移动、Web 和桌面应用。在 Flutter 的滚动组件中&#xff0c;SliverIgnorePointer 是一个用来包…...

编程日记 2024/6/5 10:58:37

比较两台计算机上的LabVIEW、工具包及驱动程序的一致性

比较两台计算机上的LabVIEW、工具包及驱动程序是否相同&#xff0c;可以通过以下步骤实现&#xff1a; 1. 检查LabVIEW版本 方法一&#xff1a;在LabVIEW中查看版本信息 步骤&#xff1a; 打开LabVIEW。点击菜单栏的 Help > About LabVIEW。记录显示的LabVIEW版本号和许可…...

编程日记 2024/6/5 10:54:31

参考——温湿度传感器DHT11驱动_STM32

设备&#xff1a;stm32f407ZGT6 环境&#xff1a;FreeRTOS HAL 到网上找DHT11的驱动&#xff0c;但是都无法使用。原因是RTOS环境中&#xff0c;由于多线程&#xff0c;使用循环计数阻塞式的delay_us延时函数就没那么准&#xff0c;且不同设备中delay_us的计数值不一样…...

编程日记 2024/6/5 10:50:25

架构每日一学 14：架构师如何进行可行性探索？

架构活动中&#xff0c;如果不进行可行性探索可能会导致重大失误&#xff0c;为企业发展带来风险。 可行性探索是架构活动的最后一个节点&#xff0c;在这之后的架构活动就像是离弦之箭&#xff0c;即便发现重大风险也很难再回头了。 互联网公司之间的竞争非常激烈&#xff0…...

编程日记 2024/6/5 10:48:22

多线程知识-13

为什么应该在循环中检查等待条件 为了实现多线程的同步和协调&#xff0c;通常使用等待和唤醒机制。在等待和唤醒机制中&#xff0c;等待条件是指一个线程等待某个条件的满足&#xff0c;当条件满足时&#xff0c;线程被唤醒继续执行。 在循环中检查等待条件的目的是为了避免虚…...

编程日记 2024/6/5 10:46:20

vue3+cli-service配置代理，跨域请求

一、配置代理端口和代理转发 在vue.config.js文件中 const {defineConfig} require(vue/cli-service)module.exports defineConfig({devServer: {host: 0.0.0.0,port: 8088, // 启动端口号proxy: {/api: { // 请求接口中要替换的标识target: , // 代理地址&#xff0c;后…...

编程日记 2024/6/5 10:44:18

git介绍、安装、配置

文章目录 1. GIT介绍2. 使用GIT的好处3. GIT 安装4. GIT 配置4.1 GIT 初始化设置、命令别名设置4.2 如果终端安装了oh-my-zsh&#xff0c;会带一堆git命令别名4.3 GIT配置文件介绍4.3.1 Linux、Mac OS系统4.3.2 windows系统 5. git设置远程仓库账号密码(拉取、上传代码不用输入…...

编程日记 2024/6/5 10:42:14

打开flutter调试

debugPaintSizeEnabled true; debugPaintBaselinesEnabled true;...

编程日记 2024/6/5 10:41:12

【前端 - Vue】Vuex基础入门，创建仓库的详细步骤

&#x1f680; 个人简介&#xff1a;6年开发经验&#xff0c;现任职某国企前端负责人&#xff0c;分享前端相关技术与工作常见问题~ &#x1f49f; 作 者&#xff1a;前端菜鸟的自我修养❣️ &#x1f4dd; 专 栏&#xff1a;vue从基础到起飞 &#x1f308; 若有帮助&…...

编程日记 2024/6/5 10:39:10

#01 Stable Diffusion基础入门：了解AI图像生成

文章目录 前言什么是Stable Diffusion?Stable Diffusion的工作原理如何使用Stable Diffusion?Stable Diffusion的应用场景结论 前言 在当今迅速发展的人工智能领域&#xff0c;AI图像生成技术以其独特的魅力吸引了广泛的关注。Stable Diffusion作为其中的一项前沿技术&#…...

编程日记 2024/6/5 10:38:08

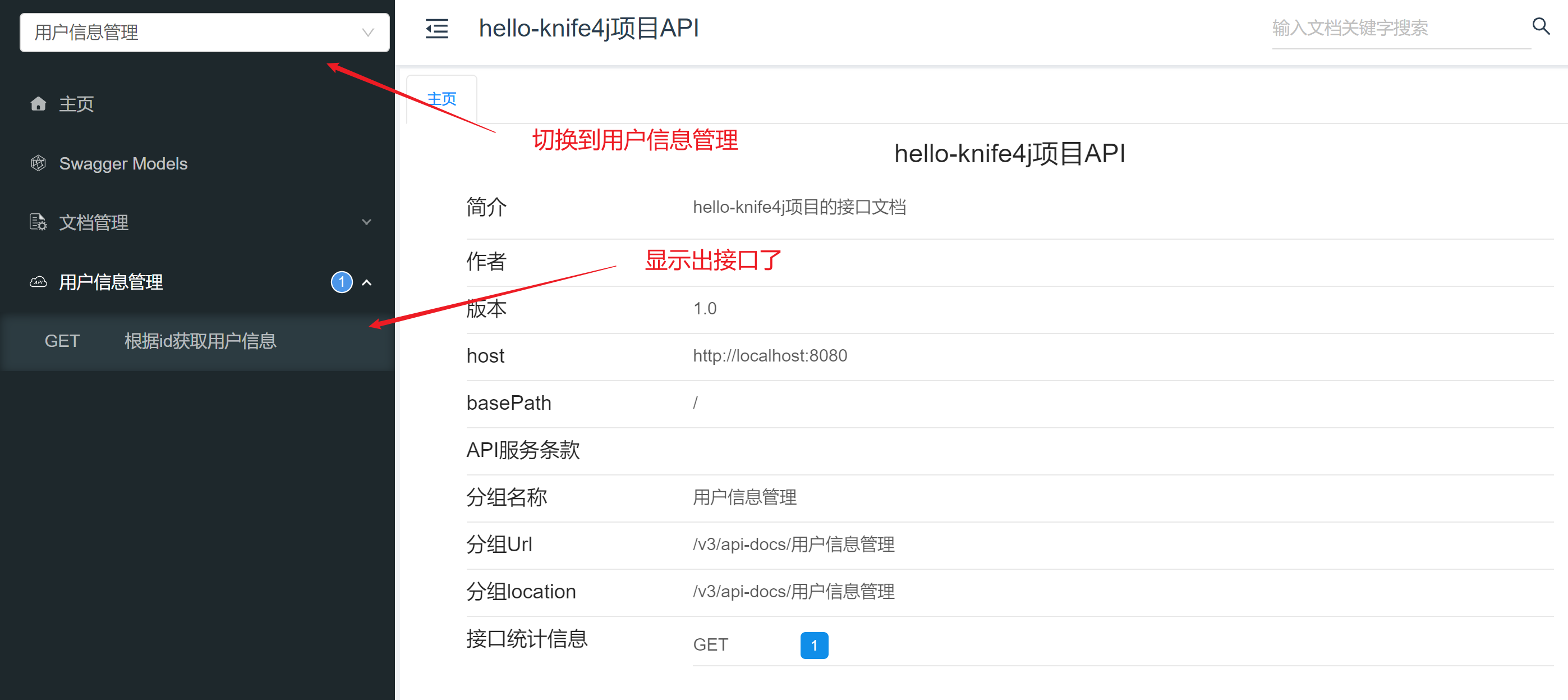
Knife4j使用

Knife4j使用 文章目录 Knife4j使用1、Knife4j介绍2、SpringBoot集成Knife4j3、基本使用 1、Knife4j介绍 Knife4j是一个用于生成和展示API文档的工具&#xff0c;同时它还提供了在线调试的功能&#xff0c;可以看作是Swagger的升级版&#xff0c;界面也比Swagger更好看&#xf…...

编程日记 2024/6/5 10:35:04

一文读懂银行承兑汇票：从申请到使用全攻略

银行承兑汇票&#xff08;Banks Acceptance Bill&#xff0c;BA&#xff09;是商业汇票的一种。它是由在承兑银行开立存款账户的存款人出票&#xff0c;向开户银行申请并经银行审查同意承兑的&#xff0c;保证在指定日期无条件支付确定的金额给收款人或持票人的票据。银行承兑汇…...

编程日记 2024/6/5 10:31:55

唯众智联网（AIoT）应用开发教学实训解决方案

一、引言 随着信息技术的飞速发展&#xff0c;物联网&#xff08;IoT&#xff09;和人工智能&#xff08;AI&#xff09;技术逐渐融合&#xff0c;形成了智联网&#xff08;AIoT&#xff09;这一新兴领域。智联网通过智能化设备、传感器、云计算等技术手段&#xff0c;实现了数…...

编程日记 2024/6/5 10:30:54

归纳跨域几种解决方案

什么是跨域&#xff1f; **说起跨域&#xff0c;就要知道什么是浏览器同源策略 **浏览器同源策略&#xff1a;必须是协议、域名、端口完全一致的才符合同源策略 **如果以上三项&#xff0c;有一项不同都涉及到跨域问题 为什么浏览器要设置同源策略呢&#xff1f; 没有同源策…...

编程日记 2024/6/5 10:29:53

LeetCode刷题第3题（C#）

给定一个字符串 s &#xff0c;请你找出其中不含有重复字符的 最长子串的长度。 法一&#xff1a; 这道题用到的其实是滑动窗口。 滑动窗口算法是在特定窗口大小的数组或字符串上执行要求的操作。它可以将一部分问题中的嵌套循环转变为一个单循环&#xff0c;以此减少时间复…...

编程日记 2024/6/5 10:28:51

了解一下Ubuntu Linux

1.3.1 什么是Ubuntu Ubuntu这个名字非常神奇&#xff0c;它取自非洲南部祖鲁语的ubuntu&#xff0c;是一个哲学名称&#xff0c;其意思为“人性”或者“我的存在是因为大家的存在”。对于中国人来说&#xff0c;一般称呼它为乌班图。 Ubuntu是在Debian的基础上开发出来的&am…...

编程日记 2024/6/5 10:27:50

K8S认证|CKS题库+答案| 11. AppArmor

目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作&#xff1a; 1&#xff09;、切换集群 2&#xff09;、切换节点 3&#xff09;、切换到 apparmor 的目录 4&#xff09;、执行 apparmor 策略模块 5&#xff09;、修改 pod 文件 6&#xff09;、…...

编程新知 2026/1/29 2:11:35

【JavaEE】-- HTTP

1. HTTP是什么&#xff1f; HTTP&#xff08;全称为"超文本传输协议"&#xff09;是一种应用非常广泛的应用层协议&#xff0c;HTTP是基于TCP协议的一种应用层协议。 应用层协议&#xff1a;是计算机网络协议栈中最高层的协议&#xff0c;它定义了运行在不同主机上…...

编程新知 2026/2/8 22:56:45

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达

先前我们总结了浏览器选区模型的交互策略&#xff0c;并且实现了基本的选区操作&#xff0c;还调研了自绘选区的实现。那么相对的&#xff0c;我们还需要设计编辑器的选区表达&#xff0c;也可以称为模型选区。编辑器中应用变更时的操作范围&#xff0c;就是以模型选区为基准来…...

编程新知 2026/1/16 16:34:26

【HarmonyOS 5.0】DevEco Testing：鸿蒙应用质量保障的终极武器

——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的​​一体化测试平台​​&#xff0c;覆盖应用全生命周期测试需求&#xff0c;主要提供五大核心能力&#xff1a; ​​测试类型​​​​检测目标​​​​关键指标​​功能体验基…...

编程新知 2026/1/28 8:17:53

Linux云原生安全：零信任架构与机密计算

Linux云原生安全&#xff1a;零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言&#xff1a;云原生安全的范式革命 随着云原生技术的普及&#xff0c;安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测&#xff0c;到2025年&#xff0c;零信任架构将成为超…...

编程新知 2025/8/17 17:11:47

CRMEB 框架中 PHP 上传扩展开发：涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云

目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

编程新知 2025/12/30 22:56:56

AspectJ 在 Android 中的完整使用指南

一、环境配置&#xff08;Gradle 7.0 适配&#xff09; 1. 项目级 build.gradle // 注意&#xff1a;沪江插件已停更&#xff0c;推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

编程新知 2025/7/7 22:33:57

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台

🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型（LLM）的广泛应用，开发者常面临多个挑战： 各大模型（OpenAI、Claude、Gemini、Ollama）接口风格不统一；缺乏一个统一平台进行模型调用与测试；本地模型 Ollama 的集成与前…...

编程新知 2026/1/25 3:31:07

html css js网页制作成品——HTML+CSS榴莲商城网页设计（4页）附源码

目录 一、&#x1f468;‍&#x1f393;网站题目 二、✍️网站描述 三、&#x1f4da;网站介绍 四、&#x1f310;网站效果 五、&#x1fa93; 代码实现 &#x1f9f1;HTML 六、&#x1f947; 如何让学习不再盲目 七、&#x1f381;更多干货 一、&#x1f468;‍&#x1f…...

编程新知 2026/2/11 3:45:10

2025季度云服务器排行榜

在全球云服务器市场&#xff0c;各厂商的排名和地位并非一成不变&#xff0c;而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势&#xff0c;对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析&#xff1a; 一、全球“三巨头”…...

编程新知 2026/2/10 10:23:55