支持向量机、随机森林、K最近邻和逻辑回归-九五小庞
支持向量机(Support Vector Machine, SVM)、随机森林(Random Forest)、K最近邻(K-Nearest Neighbors, KNN)和逻辑回归(Logistic Regression)是机器学习和统计学习中常用的分类算法。以下是这些算法的简要介绍:
1. 支持向量机(SVM)
原理:
- SVM是一种监督学习算法,主要用于数据分类问题。
- 在高维空间中寻找一个超平面(在二维空间中为一条直线,三维空间中为一个平面)来对训练样本进行划分,使得不同类别的样本尽可能位于超平面的两侧,同时最大化两侧最近点到超平面的距离。
- 这些最近的点被称为支持向量。
特点:
- 对高维数据有效。
- 在数据维度大于样本数时仍表现良好(即小样本学习)。
- 可以使用核函数来处理非线性问题。
2. 随机森林(Random Forest)
原理:
- 随机森林是决策树算法的一种集成学习方法。
- 通过构建多个决策树并汇总它们的预测结果来进行分类或回归。
- 每个决策树基于原始数据集中随机抽取的样本和特征子集进行训练。
特点:
- 准确性高,不易过拟合。
- 可以处理高维数据。
- 可以评估特征的重要性。
- 对缺失值不敏感。
3. K最近邻(KNN)
原理:
- KNN是一种基于实例的学习,或者说是局部逼近和将所有计算推迟到分类之后进行的惰性学习。
- 一个样本的类别由其邻居的类别投票决定,其中邻居是指训练集中与该样本最相似的K个样本。
- 相似度通常通过计算样本之间的欧氏距离或其他距离度量来确定。
特点:
- 原理简单,易于理解。
- 对异常值敏感。
- 计算量大,特别是当数据集很大时。
- 需要选择合适的K值。
4. 逻辑回归(Logistic Regression)
原理:
- 逻辑回归虽然名字中有“回归”,但实际上是一种分类算法。
- 它通过逻辑函数(sigmoid函数)将线性回归模型的输出转换为介于0和1之间的概率值,进而进行二分类或多分类。
特点:
- 计算效率高,易于实现。
- 对分类问题的解释性强。
- 可以直接给出类别的概率。
- 但在处理非线性问题时需要特征转换或核方法。
这些算法各有优缺点,适用于不同的场景和数据集。在实际应用中,需要根据问题的具体需求和数据的特性来选择合适的算法。
相关文章:

支持向量机、随机森林、K最近邻和逻辑回归-九五小庞
支持向量机(Support Vector Machine, SVM)、随机森林(Random Forest)、K最近邻(K-Nearest Neighbors, KNN)和逻辑回归(Logistic Regression)是机器学习和统计学习中常用的分类算法。…...

MySQL—多表查询—多表关系介绍
一、引言 提到查询,我们想到之前学习的单表查询(DQL语句)。而这一章节部分的博客我们将要去学习和了解多表查询。 对于多表查询,主要从以下7个方面进行学习。 (1)第一部分:介绍 1、多表关系 2、…...

Vue基础篇--table的封装
1、 在components文件夹中新建一个ITable的vue文件 <template><div class"tl-rl"><template :table"table"><el-tablev-loading"table.loading":show-summary"table.hasShowSummary":summary-method"table…...

mysql中optimizer trace的作用
大家好。对于MySQL 5.6以及之前的版本来说,查询优化器就像是一个黑盒子一样,我们只能通过EXPLAIN语句查看到最后 优化器决定使用的执行计划,却无法知道它为什么做这个决策。于是在MySQL5.6以及之后的版本中,MySQL新增了一个optimi…...

实习面试题(答案自敲)、
1、为什么要重写equals方法,为什么重写了equals方法后,就必须重写hashcode方法,为什么要有hashcode方法,你能介绍一下hashcode方法吗? equals方法默认是比较内存地址;为了实现内容比较,我们需要…...

二叉树讲解
目录 前言 二叉树的遍历 层序遍历 队列的代码 queuepush和queuepushbujia的区别 判断二叉树是否是完全二叉树 前序 中序 后序 功能展示 创建二叉树 初始化 销毁 简易功能介绍 二叉树节点个数 二叉树叶子节点个数 二叉树第k层节点个数 二叉树查找值为x的节点 判…...
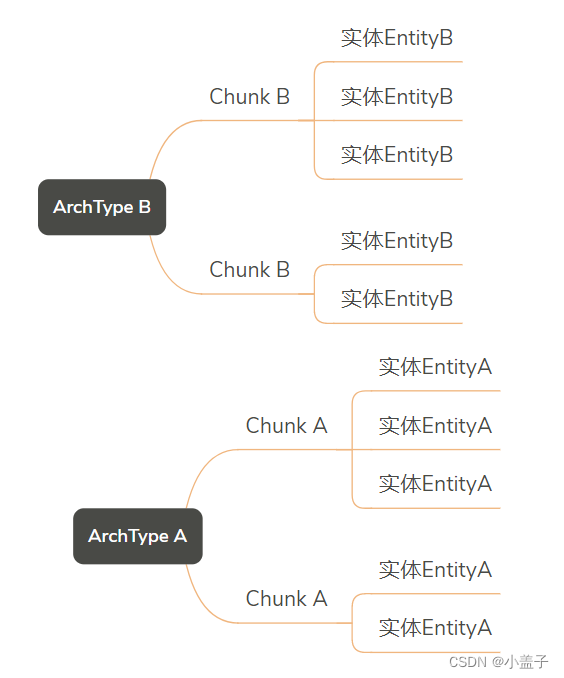
Unity DOTS技术(五)Archetype,Chunk,NativeArray
文章目录 一.Chunk和Archetype什么是Chunk?什么是ArchType 二.Archetype创建1.创建实体2.创建并添加组件3.批量创建 三.多线程数组NativeArray 本次介绍的内容如下: 一.Chunk和Archetype 什么是Chunk? Chunk是一个空间,ECS系统会将相同类型的实体放在Chunk中.当一个Chunk…...

算法学习笔记(7.1)-贪心算法(分数背包问题)
##问题描述 给定 𝑛 个物品,第 𝑖 个物品的重量为 𝑤𝑔𝑡[𝑖−1]、价值为 𝑣𝑎𝑙[𝑖−1] ,和一个容量为 𝑐𝑎&…...

气膜建筑的施工对周边环境影响大吗?—轻空间
随着城市化进程的加快,建筑行业的快速发展也带来了环境问题。噪音、灰尘和建筑废料等对周边居民生活和生态环境造成了不小的影响。因此,选择一种环保高效的施工方式变得尤为重要。气膜建筑作为一种新兴的建筑形式,其施工过程对周边环境的影响…...

【计算机网络】对应用层HTTP协议的重点知识的总结
˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱ ʕ̯•͡˔•̯᷅ʔ大家好,我是xiaoxie.希望你看完之后,有不足之处请多多谅解,让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客 本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN 如…...

30分钟快速入门TCPDump
TCPDump是一款功能强大的网络分析工具,它可以帮助网络管理员捕获并分析流经网络接口的数据包。由于其在命令行环境中的高效性与灵活性,TCPDump成为了网络诊断与安全分析中不可或缺的工具。本文将详细介绍TCPDump的基本用法,并提供一些高级技巧…...

Python | 刷题日记
1.海伦公式求三角形的面积 area根号下(p(p-a)(p-b)(p-c)) p是周长的一半 2.随机生成一个整数 import random xrandom.randint(0,9)#随机生成0到9之间的一个数 yeval(input("please input:")) if xy:print("bingo") elif x<y:pri…...
“JS逆向 | Python爬虫 | 动态cookie如何破~”
案例目标 目标网址:aHR0cHMlM0EvL21hdGNoLnl1YW5yZW54dWUuY29tL21hdGNoLzI= 本题目标:提取全部 5 页发布日热度的值,计算所有值的加和,并提交答案 常规 JavaScript 逆向思路 JavaScript 逆向工程通常分为以下三步: 寻找入口:逆向工程的核心在于找出加密参数的生成方式。…...
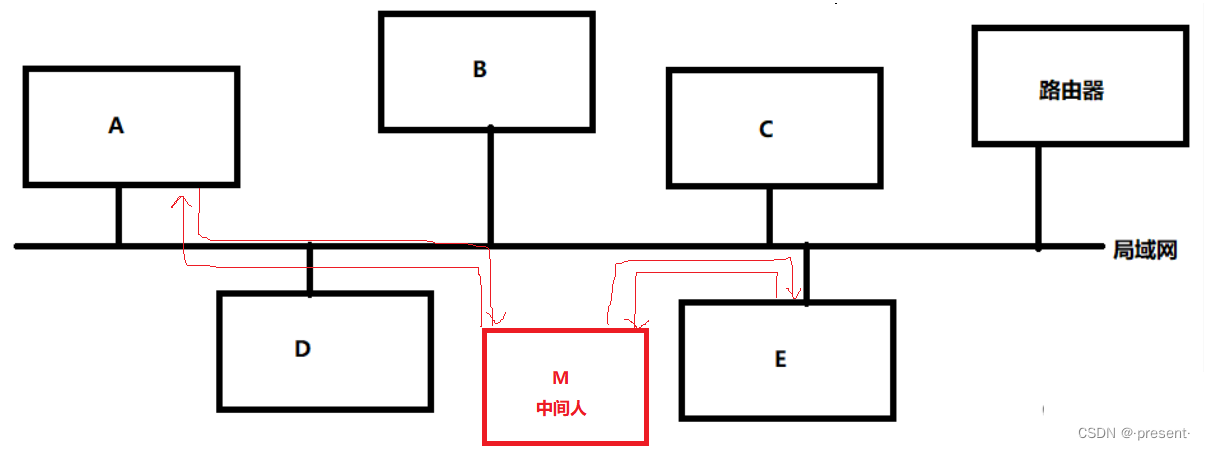
十.数据链路层——MAC/ARP
IP和数据链路层之间的关系 引言 在IP一节中,我们说IP层路由(数据转发)的过程,就像我们跳一跳游戏一样,从一个节点,转发到另一个节点 它提供了一种将数据从A主机跨网络发到B主机的能力 什么叫做跨网络??&a…...

Linux主机安全可视化运维(免费方案)
本文介绍如何使用免费的主机安全软件,在自有机房或企业网络实现对Linux系统进行可视化“主机安全”管理。 一、适用对象 本文适用于个人或企业内的Linux服务器运维场景,实现免费、高效、可视化的主机安全管理。提前发现主机存在的安全风险,全方位实时监控主机运行时入侵事…...

Vite + Vue 3 前端项目实战
一、项目创建 npm install -g create-vite #安装 Vite 项目的脚手架工具 # 或者使用yarn yarn global add create-vite#创建vite项目 create-vite my-vite-project二、常用Vue项目依赖安装 npm install unplugin-auto-import unplugin-vue-components[1] 安装按需自动导入组…...

python-字符替换
[题目描述] 给出一个字符串 s 和 q 次操作,每次操作将 s 中的某一个字符a全部替换成字符b,输出 q 次操作后的字符串输入 输入共 q2 行 第一行一个字符串 s 第二行一个正整数 q,表示操作次数 之后 q 行每行“a b”表示把 s 中所有的a替换成b输…...
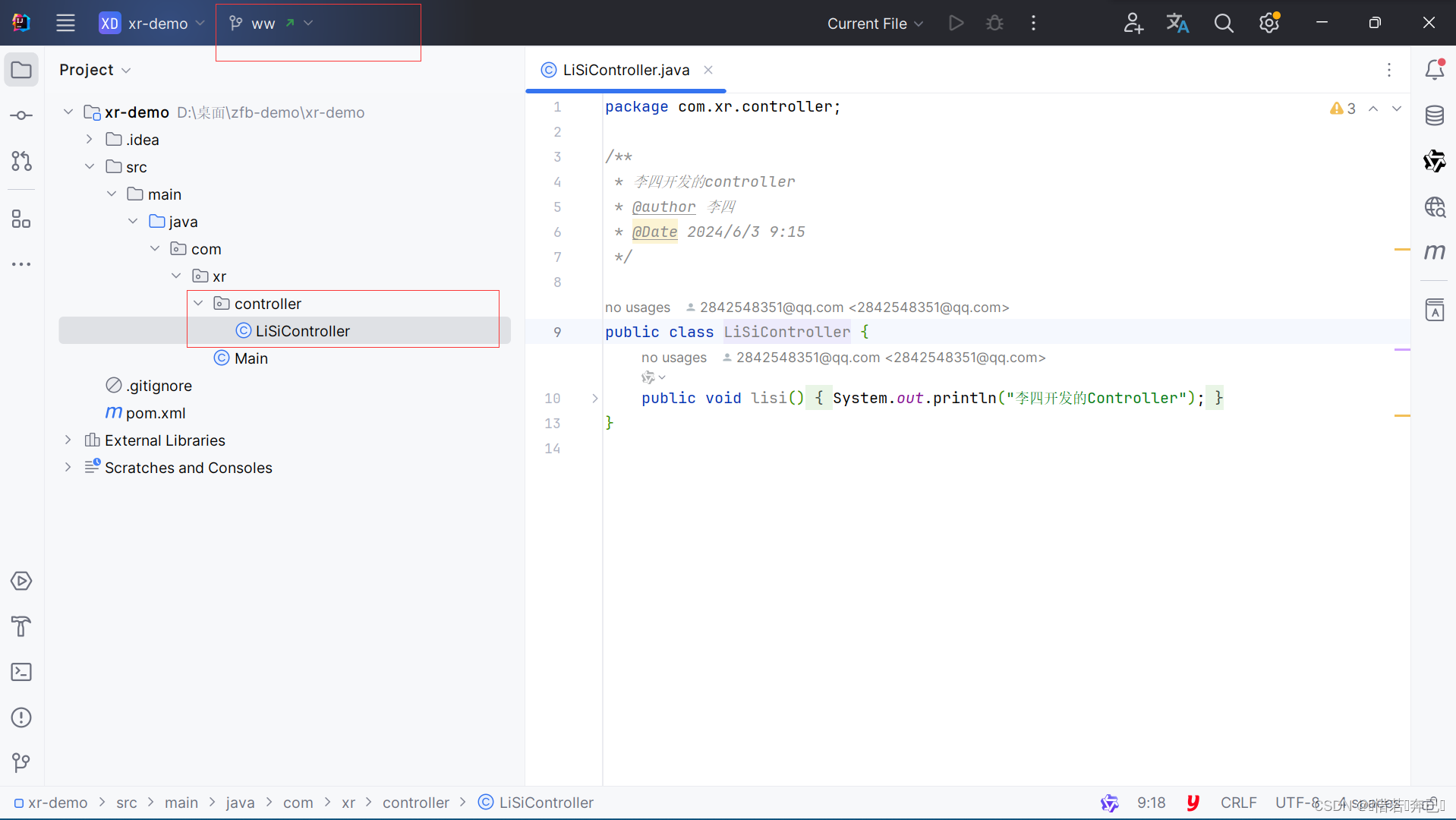
团队项目开发使用git工作流(IDEA)【精细】
目录 开发项目总体使用git流程 图解流程 1.创建项目仓库[组长完成] 2. 创建项目,并进行绑定远程仓库【组长完成】 3.将项目与远程仓库(gitee)进行绑定 3.1 创建本地的git仓库 3.2 将项目添加到缓存区 3.3 将项目提交到本地仓库&#…...

爬虫案例实战
文章目录 一、窗口切换实战二、京东数据抓取 一、窗口切换实战 案例实战:使用selenium实现打开百度和腾讯两个窗口并切换 知识点:用到selenium中execute_script()执行js代码及switch_to.window()方法 全部代码如下: import time import war…...
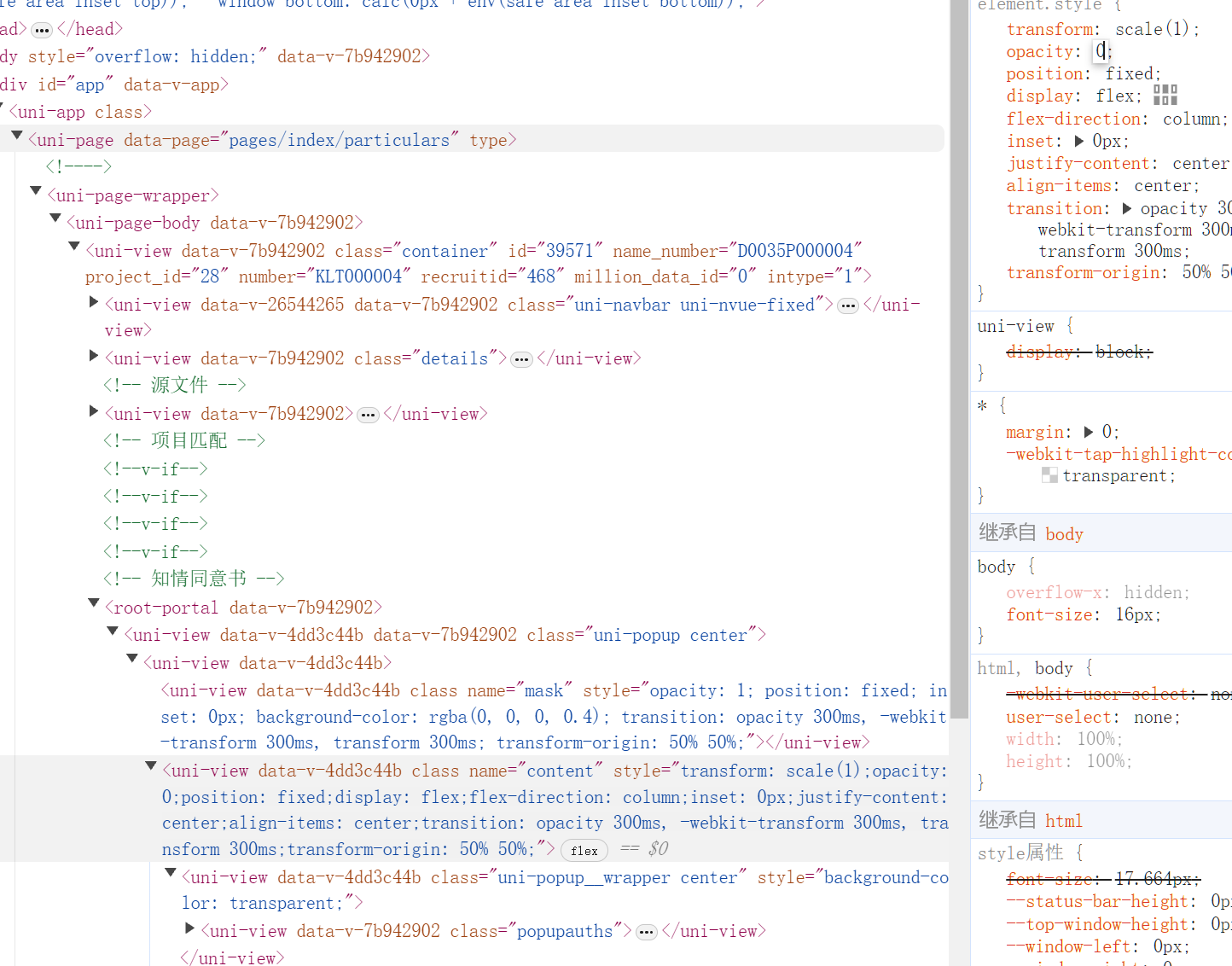
uniapp uni-popup内容被隐藏问题
今天开发新需求的时候发现uni-popup 过一会就被隐藏掉只留下遮罩(css被更改了),作者进行了如下调试。 1.讲uni-popup放入其他节点内 失败! 2.在生成dom后在打开 失败! 3.uni-popup将该节点在包裹一层 然后将统计设置样式,v-if v-s…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

字符串哈希+KMP
P10468 兔子与兔子 #include<bits/stdc.h> using namespace std; typedef unsigned long long ull; const int N 1000010; ull a[N], pw[N]; int n; ull gethash(int l, int r){return a[r] - a[l - 1] * pw[r - l 1]; } signed main(){ios::sync_with_stdio(false), …...
