STM32-- GPIO->EXTI->NVIC中断
一、NVIC简介
1、NVIC寄存器

2、中断优先级
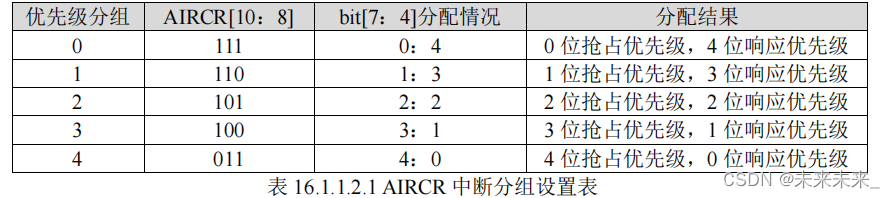
3、NVIC的使用

二、EXTI 简介

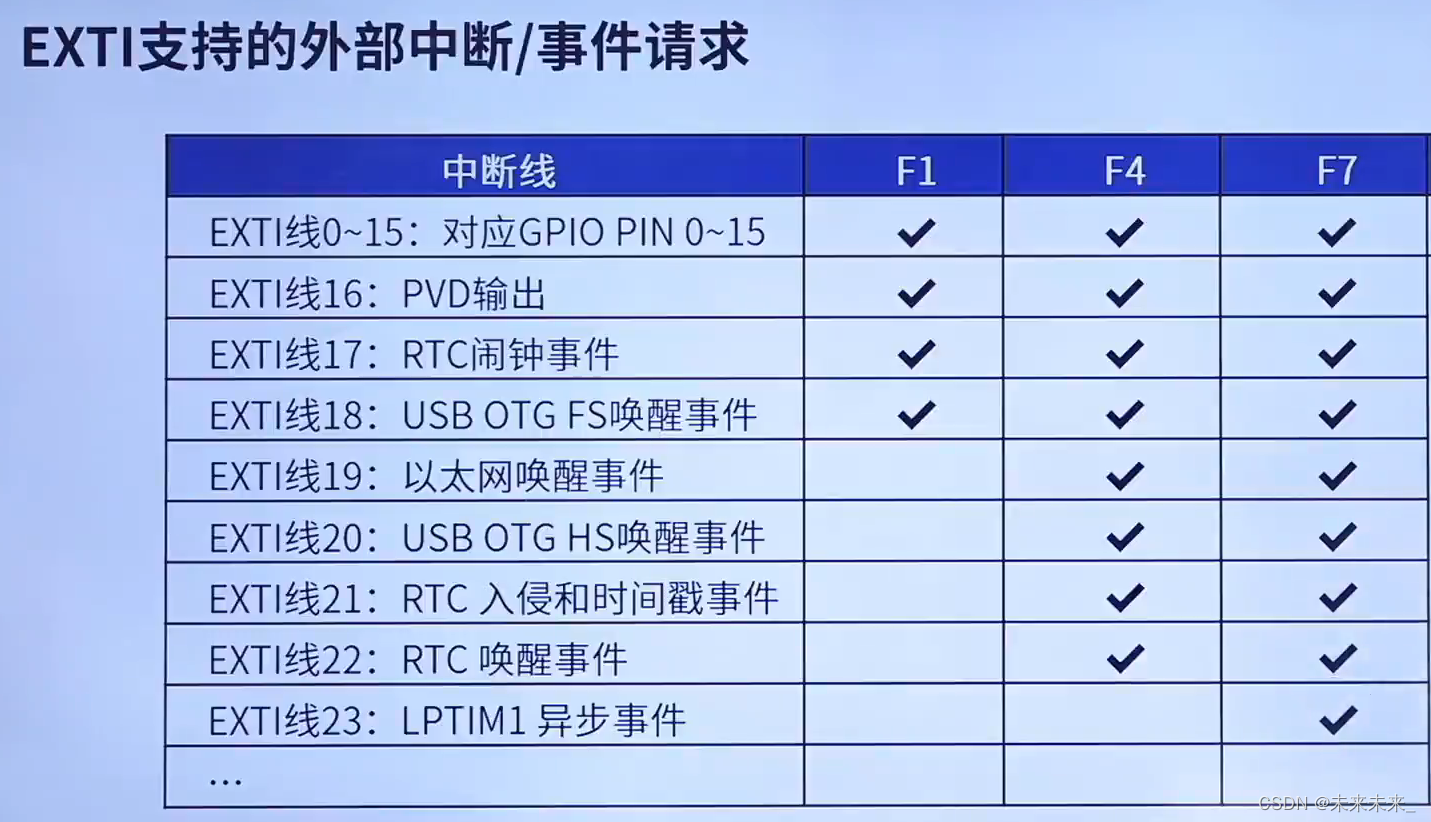
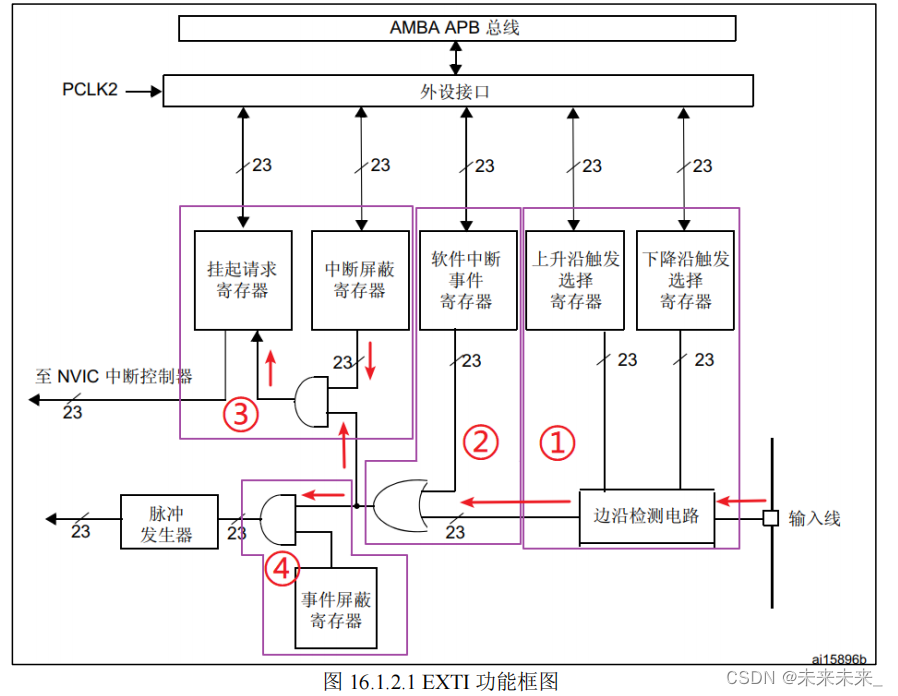

三、如何使用中断
1、EXTI中断流程
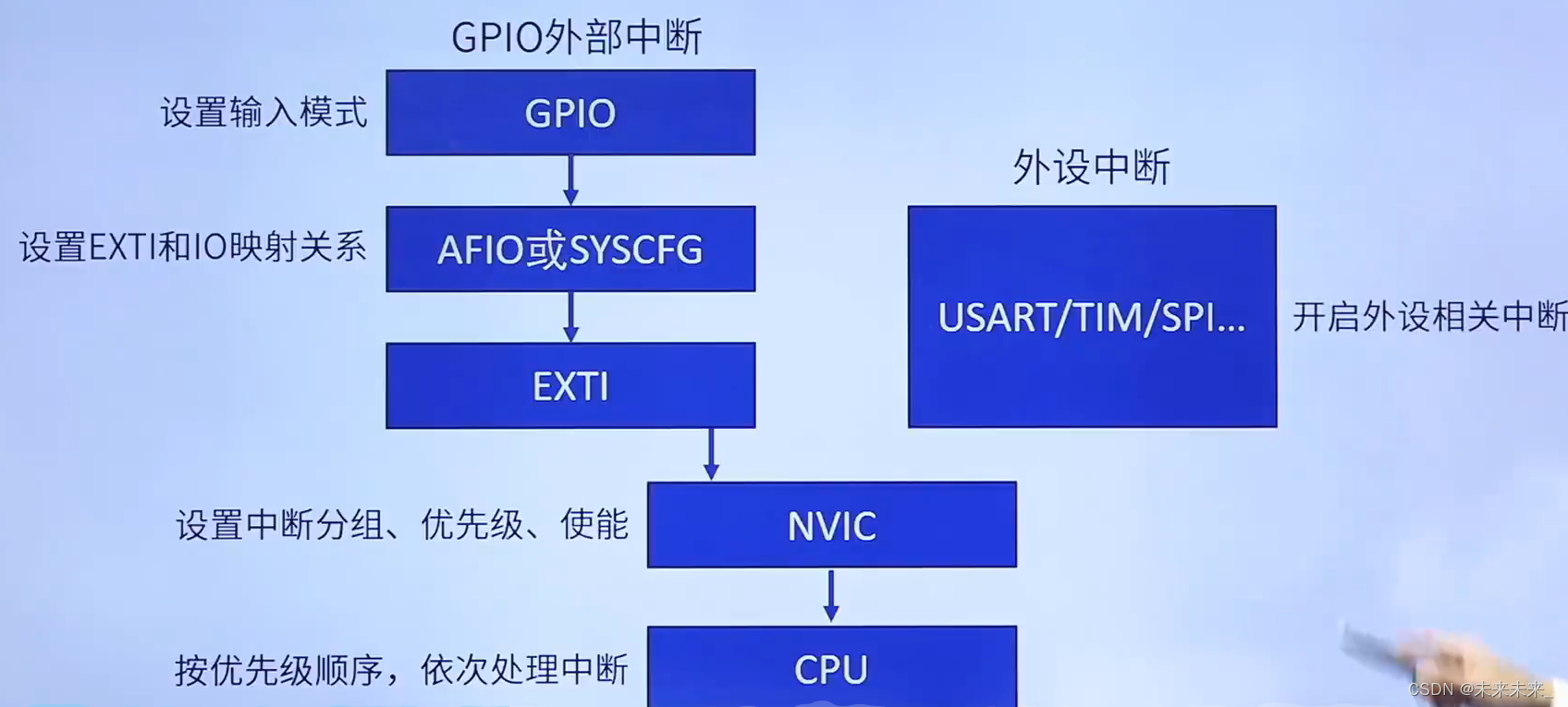
EXTI 0-15这16根线会与gpio完成映射,EXTI16、17....等输入线是其他外设中断,比如闹钟,USB等,这两者统称为EXTI中断。
2、EXTI中断配置步骤

其中步骤2-5可以使用HAL_GPIO_Init一步到位
四、HAL库中断回调处理机制
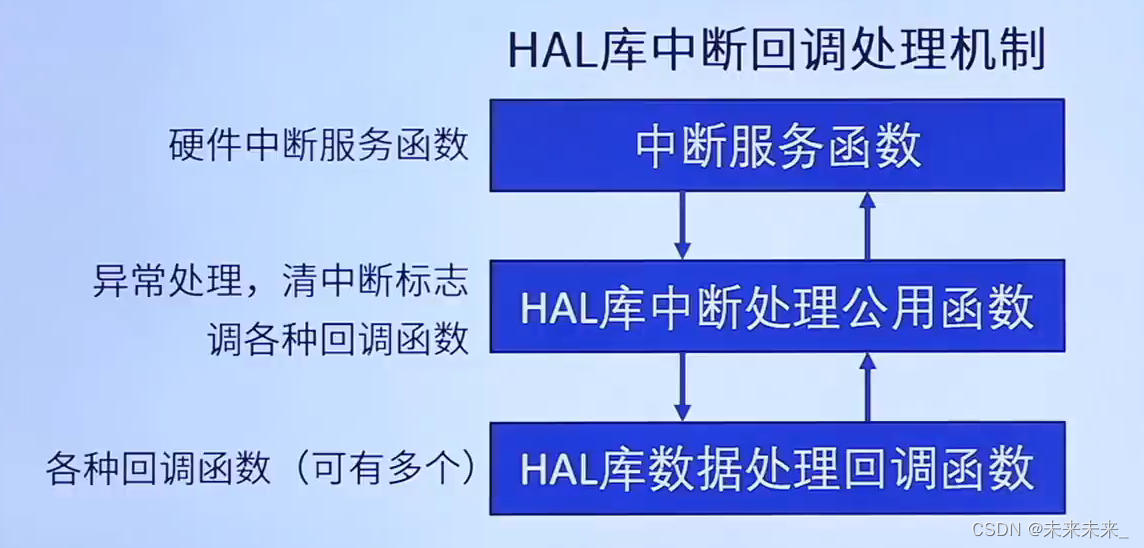
五、应用示例
应用步骤
1、看原理图确定引脚连接
2、使能IO口时钟,完成IO口与中断线的映射关系,设置优先级,设置中断服务函数处理中断,设置中断回调函数实现具体中断处理操作。
按键消抖的实现:
按键按下(GPIO中断)|v
启动定时器(复位计数器)|v定时器计时(10ms)|v
定时器计数完成(触发中断)|v
检查按键状态(确认按下)|v
停止定时器,设置标志位|v主循环处理中断事件
相关文章:

STM32-- GPIO->EXTI->NVIC中断
一、NVIC简介 什么是 NVIC ? NVIC 即嵌套向量中断控制器,全称 Nested vectored interrupt controller 。它 是内核的器件,所以它的更多描述可以看内核有关的资料。M3/M4/M7 内核都是支持 256 个中断,其中包含了 16 个系统中…...

【介绍下WebStorm开发插件】
🎥博主:程序员不想YY啊 💫CSDN优质创作者,CSDN实力新星,CSDN博客专家 🤗点赞🎈收藏⭐再看💫养成习惯 ✨希望本文对您有所裨益,如有不足之处,欢迎在评论区提出…...
推荐丨一键申请SSL证书,让网站实现HTTPS访问!
申请HTTPS证书可以简化为以下几个直接步骤,以便您能快速理解和操作: 1. 确定证书类型: - 单域名证书:适用于一个特定域名。 - 通配符证书:适用于同一主域名下的所有子域名。 - 多域名证书:覆盖多个不同的域…...

交叉导轨在医疗设备上的作用!
随着医疗器械行业的需求逐步增长,交叉导轨给医疗器械行业带来了广阔的发展前景。作为重要的精密传动元件,交叉导轨具有寿命长、高精度、高刚性、高耐腐蚀性和高稳定性等优点,满足精密仪器上对产品的高要求使用场景。 在医疗设备领域中交叉导轨…...

【云原生】Docker Compose 使用详解
目录 一、前言 二、Docker Compose 介绍 2.1 Docker Compose概述 2.2 Docker Compose特点 2.3 Docker Compose使用场景 三、Docker Compose 搭建 3.1 安装docker环境 3.2 Docker Compose安装方式一 3.2.1 下载最新版/如果不是最新可替换最新版本 3.2.2 设置权限 3.2.…...
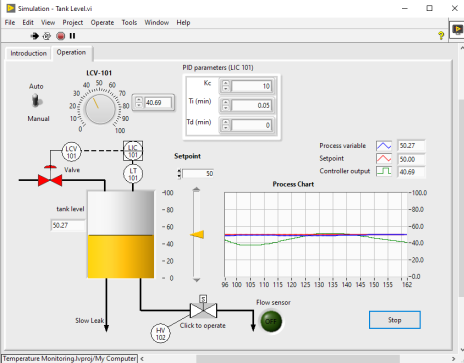
通过LabVIEW提升生产设备自动化水平
现代制造业对生产设备的自动化水平提出了越来越高的要求。使用LabVIEW这一强大的图形化编程环境,可以显著提升生产设备的自动化程度,改善生产效率和产品质量。本文将详细分析如何通过LabVIEW改善生产设备的自动化水平,并提供具体的实施策略与…...
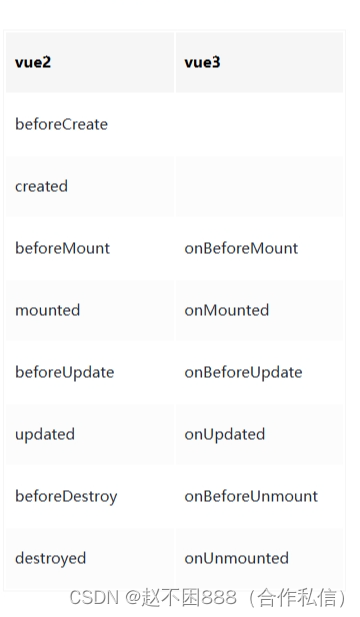
面试题vue+uniapp(个人理解-面试口头答述)未编辑完整....
1.vue2和vue3的区别(vue3与vue2的区别(你不知道细节全在这)_vue2和vue3区别-CSDN博客)参考 Vue3 在组合式(Composition )API,中使用生命周期钩子时需要先引入,而 Vue2 在选项API&am…...
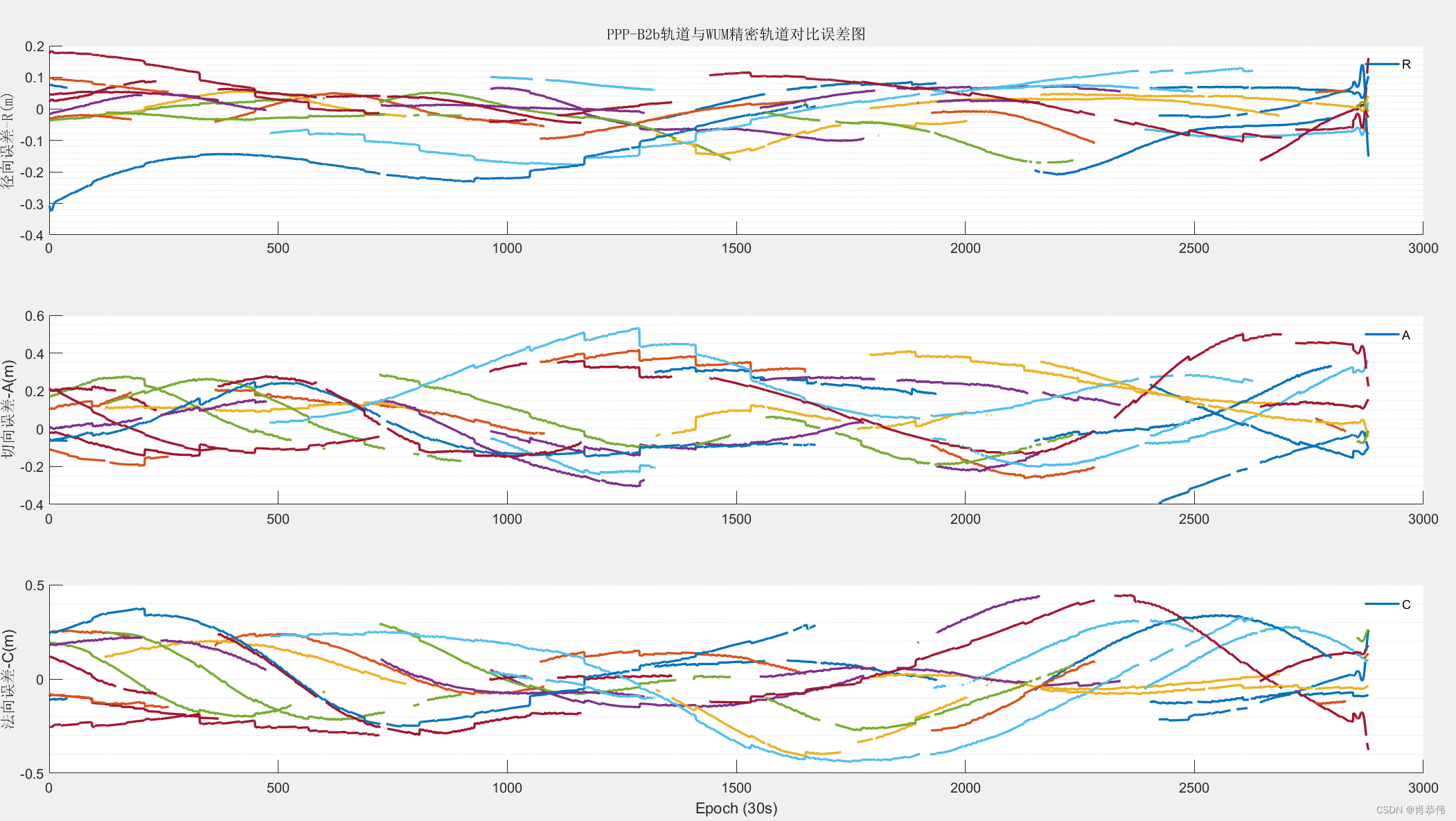
PPP-B2b精密产品使用注意事项及分析
1、因为在使用PPP-B2b进行定轨的时候,发的精密轨道产品是B3频点的,需要改正的卫星质心(Com)与SP3精密星历对比。 2、PPP-B2b产品吸收了电离层误差,因此电离层提取方面与IGS电离层完全无法对其。 3、由于PPP-B2b产品精…...
C语言(结构体)
Hi~!这里是奋斗的小羊,很荣幸各位能阅读我的文章,诚请评论指点,欢迎欢迎~~ 💥个人主页:小羊在奋斗 💥所属专栏:C语言 本系列文章为个人学习笔记,在这里撰写成文一…...
用法:深入解析与实战应用)
Python filter()用法:深入解析与实战应用
Python filter()用法:深入解析与实战应用 在Python编程中,filter() 函数是一个内置的高阶函数,它用于过滤序列,过滤掉不符合条件的元素,返回由符合条件元素组成的新列表。该函数在数据处理和筛选时非常有用࿰…...
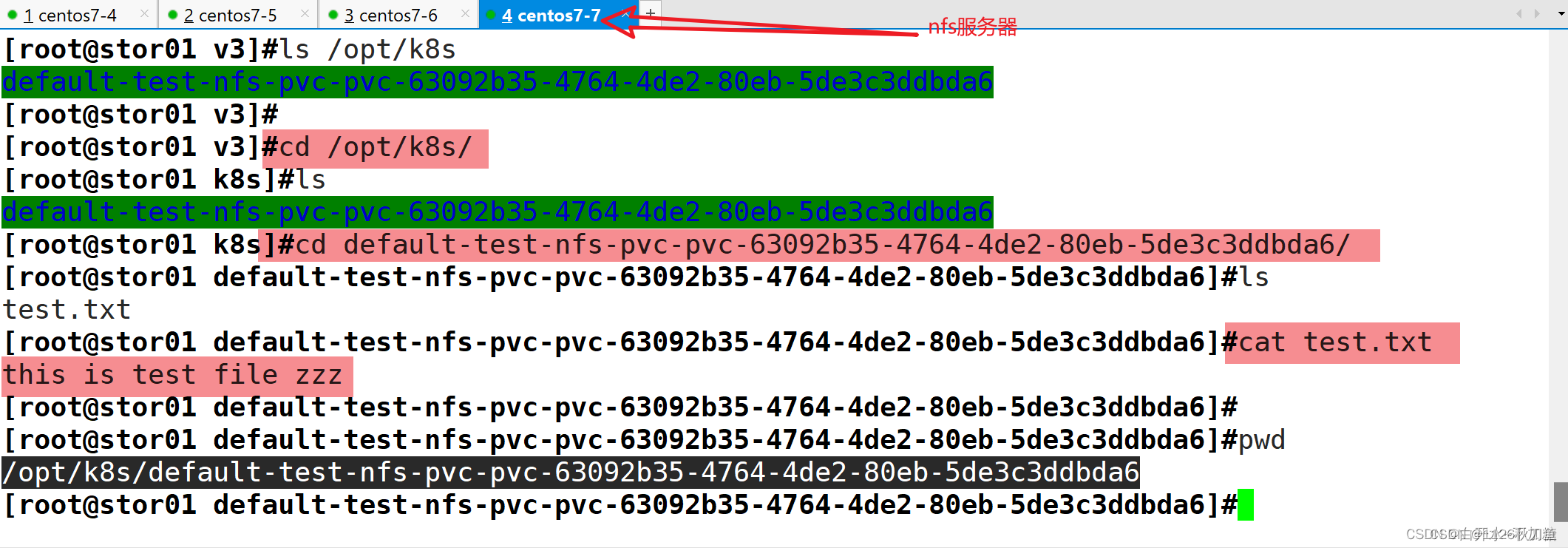
k8s集群的存储卷、pvc和pv
目录 简介 简介 PV 全称叫做 Persistent Volume,持久化存储卷。它是用来描述或者说用来定义一个存储卷的,这个通常都是由运维工程师来定义。 PVC 的全称是 Persistent Volume Claim,是持久化存储的请求。它是用来描述希望使用什么样的或者说…...

二分搜索树深度优先遍历
二分搜索树深度优先遍历 二分搜索树(Binary Search Tree,简称BST)是一种特殊的二叉树,它具有以下特性:对于树中的任意节点,其左子树中的所有元素都小于该节点的值,其右子树中的所有元素都大于该…...

ImportError: cannot import name ‘packaging‘ from ‘pkg_resources‘‘
参考自: [Bug]: ImportError: cannot import name packaging from pkg_resources (/usr/local/lib/python3.10/dist-packages/pkg_resources/__init__.py) Issue #15863 AUTOMATIC1111/stable-diffusion-webui GitHub ImportError: cannot import name packaging from pkg…...

灯塔歌曲音乐下载官网
灯塔歌曲音乐下载官网网址:www.dengtamp3.com 灯塔音乐下载上线以“用心服务,认真负责”为核心价值。 我们的团队是一个青春的团队,朝气蓬勃。我们采用最新的服务模式,以网为媒为广大客户提供服务,我们坚持以“用心&a…...

数据结构的归并排序(c语言版)
一.归并排序的基本概念 1.基本概念 归并排序是一种高效的排序算法,它采用了分治的思想。它的基本过程如下: 将待排序的数组分割成两个子数组,直到子数组只有一个元素为止。然后将这些子数组两两归并,得到有序的子数组。不断重复第二步,直到最终得到有序的整个数组。 2.核心…...

ubuntu使用Docker笔记
一、参考资料 1、B站视频 尚硅谷Docker实战教程 2、有心人整理的笔记 Docker笔记(周阳版) 3、菜鸟教程 Docker 教程 以下是本人的折腾实践。 二、Docker的安装 2.1、使用清华源安装docker,清华源官方教程。 本人是在ubuntu20.04下安装的…...

PHP编程入门:揭开Web开发的神秘面纱
PHP编程入门:揭开Web开发的神秘面纱 在数字化时代,PHP作为一种广泛使用的服务器端脚本语言,为Web开发领域注入了强大的活力。无论你是编程新手还是有一定经验的开发者,掌握PHP编程都将为你开启一扇通往Web开发新世界的大门。接下…...
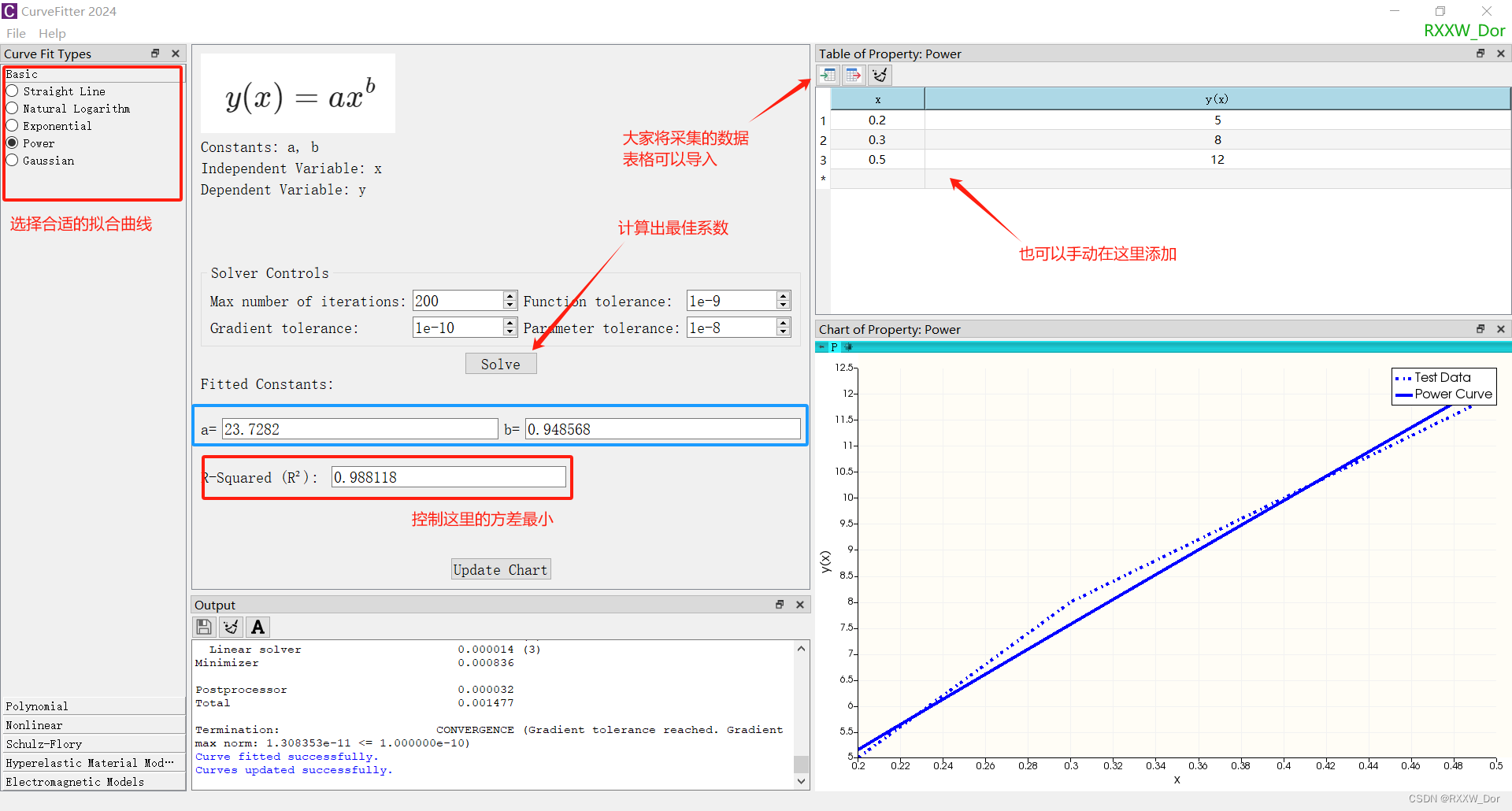
曲线拟合工具软件(免费)
曲线拟合是数据处理中经常用到的数值方法,本质是使用某一个模型(方程或者方程组)将一系列离散的数据拟合成平滑的曲线或者曲面,数值求解出对应的函数参数,大家可以利用MATLAB的曲线拟合工具箱也可以使用第三方的拟合软件,今天我们介绍Welsim免费的曲线拟合软件 1、MATLA…...
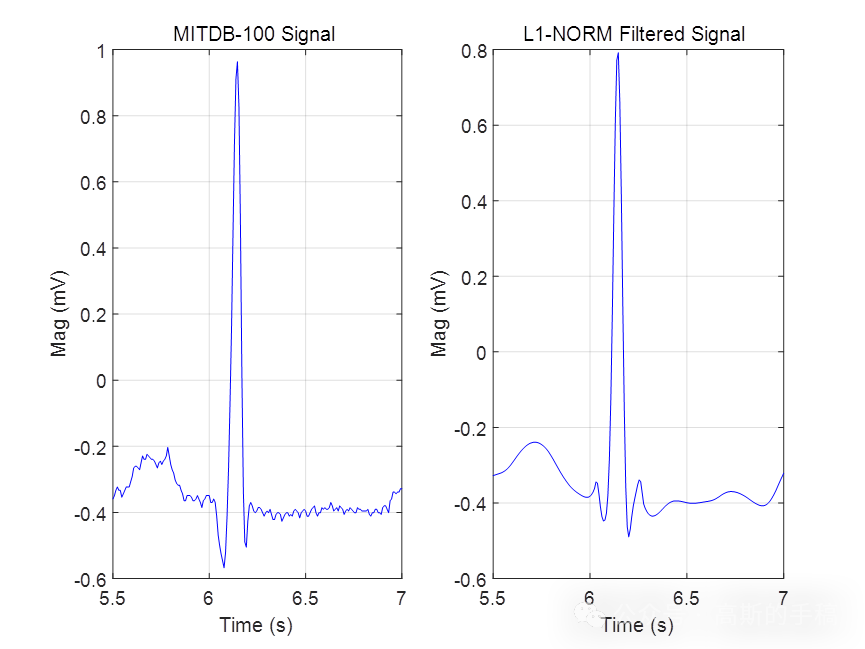
基于L1范数惩罚的稀疏正则化最小二乘心电信号降噪方法(Matlab R2021B)
L1范数正则化方法与Tikhonov正则化方法的最大差异在于采用L1范数正则化通常会得到一个稀疏向量,它的非零系数相对较少,而Tikhonov正则化方法的解通常具有所有的非零系数。即:L2范数正则化方法的解通常是非稀疏的,并且解的结果在一…...
)
Bitbucket的原理及应用详解(一)
本系列文章简介: 在数字化和全球化的今天,软件开发和项目管理已经成为企业成功的关键因素之一。随着团队规模的扩大和项目的复杂化,如何高效地协同开发、管理代码和确保代码质量成为了开发者和管理者面临的重要挑战。Bitbucket作为一款功能强…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...
