多角度剖析事务和事件的区别
事务和事件这两个概念在不同的领域有着不同的含义,尤其是在计算机科学、数据库管理和软件工程中。下面从多个角度来剖析事务和事件的区别:
计算机科学与数据库管理中的事务
事务(Transaction):
- 定义:在数据库管理中,事务被视为一系列操作的集合,这些操作作为一个整体被提交或回滚。这意味着所有操作要么全部成功完成,要么因为任何失败而全部撤销,确保数据的一致性和完整性。
- 特征:事务具有ACID特性,即原子性(Atomicity)、一致性(Consistency)、隔离性(Isolation)和持久性(Durability)。
- 用途:事务用于保证数据处理的可靠性和安全性,特别是在并发环境或需要数据完整性的场景下。
计算机编程与用户交互中的事件
事件(Event):
- 定义:在计算机编程中,事件通常是由用户的动作或者系统内部状态变化引发的信号。例如,点击鼠标、按下键盘键、文件系统变化等。
- 特征:事件是被动的,它们等待被触发,然后由事件监听器或处理器响应。
- 用途:事件驱动编程模型允许程序对特定事件作出反应,从而实现交互性和响应性。
实体与抽象概念上的区分
- 事务:在更广泛的意义上,事务可以指任何具体的、需要处理的业务或行政活动,比如银行转账、合同签订等。
- 事物/事件:事物通常指的是客观存在的实体或现象,而事件则是在特定时间和地点发生的具体事情。事物是静态的描述,事件是动态的过程。
法律和日常用语中的区分
在法律和日常交流中,“事务”通常指的是需要处理的事项,可能涉及行政、商业或个人的活动。“事件”则指的是在某个时间点或时间段内发生的特定情况或事故。
您的理解在一定程度上是对的,但需要稍微调整一下概念的适用范围,以更加准确地反映事务和事件的本质。
事务——过程与状态转换
确实,事务在很多情况下可以看作是一个过程。尤其在数据库管理和事务处理的上下文中,事务是指一系列的操作,这些操作作为一个整体执行,涉及到数据的状态转换。事务的开始和结束定义了一个明确的过程边界,在这个过程中,数据从一种一致状态转换到另一种一致状态。因此,可以说事务是一个确保数据完整性和一致性的过程。
事件——触发与结果
事件则更倾向于描述一个触发点或结果。在计算机编程中,事件通常是外部条件变化的结果,如用户的输入、硬件的中断或其他程序的信号。事件发生后,系统或程序会根据预定义的规则或逻辑进行响应,这可能包括执行一系列的动作或更新系统状态。因此,事件可以看作是导致系统状态改变的触发因素,或是状态改变本身的结果。
结合与差异
将事务视为过程,事件视为结果或触发点,这种理解方式在某些情境下是有道理的。然而,需要注意的是,事务和事件之间的界限并不总是那么清晰。在某些情况下,一个事务的完成也可以视为一个事件,因为它标志着状态的显著变化,并可能触发后续的处理流程。
总结
事务和事件在多个层面上有不同的含义和用途:
-
事务关注的是操作的完整性和一致性,常见于数据库管理和交易处理。
-
事件关注的是状态的变化和系统的响应,常见于用户界面和事件驱动的软件架构。
-
在非技术语境下,“事务”更多地关联于需要处理的业务或行政工作,而“事件”关联于发生的具体事情或事故。
-
事务强调的是一个过程,它涉及到数据或状态的有序转换,确保操作的原子性、一致性、隔离性和持久性。
-
事件强调的是状态的改变或外部条件的触发,它是系统响应的起点,可以引发一系列后续的处理或操作。
相关文章:

多角度剖析事务和事件的区别
事务和事件这两个概念在不同的领域有着不同的含义,尤其是在计算机科学、数据库管理和软件工程中。下面从多个角度来剖析事务和事件的区别: 计算机科学与数据库管理中的事务 事务(Transaction): 定义:在数据库管理中,…...
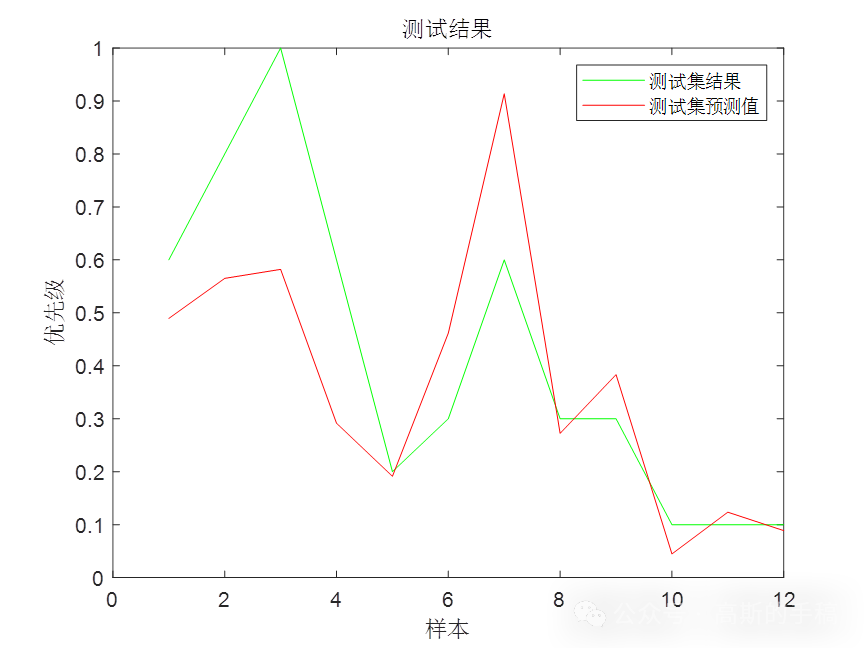
模糊小波神经网络(MATLAB 2018)
模糊系统是一种基于知识或规则的控制系统,从属于智能控制,通过简化系统的复杂性,利用控制法来描述系统变量之间的关系,采用语言式的模糊变量来描述系统,不必对被控对象建立完整的数学模型。相比较传统控制策略…...

HTML布局
标准流: 标准流就是元素在页面中的默认排列方式,也就是元素在页面中的默认位置。 1.1 块元素----独占一行----从上到下排列 1.2 行内元素----不独占一行----从左到右排列,遇到边界换行 1.3 行内块元素----不独占一行…...

数据结构:双链表
数据结构:双链表 题目描述参考代码 题目描述 输入样例 10 R 7 D 1 L 3 IL 2 10 D 3 IL 2 7 L 8 R 9 IL 4 7 IR 2 2输出样例 8 7 7 3 2 9参考代码 #include <iostream>using namespace std;const int N 100010;int m; int idx, e[N], l[N], r[N];void init…...

Python3 元组、列表、字典、集合小结
前言 本文主要对Python中的元组、列表、字典、集合进行小结,主要内容包括知识点回顾、异同点、使用场景。 文章目录 前言一、知识点回顾1、列表(List)2、 元组(Tuple)3、 字典(Dictionary)4.、…...

2024会声会影破解免费序列号,激活全新体验!
会声会影2024序列号注册码是一款专业的视频编辑软件,它以其强大的功能和易用性受到了广大用户的喜爱。在这篇文章中,我将详细介绍会声会影2024序列号注册码的功能和特色,帮助大家更好地了解这款产品。 会声会影全版本绿色安装包获取链接&…...
机器学习18个核心算法模型
1. 线性回归(Linear Regression) 用于建立自变量(特征)和因变量(目标)之间的线性关系。 核心公式: 简单线性回归的公式为: , 其中 是预测值, 是截距, 是斜…...
)
平滑值(pinghua)
平滑值 题目描述 一个数组的“平滑值”定义为:相邻两数差的绝对值的最大值。 具体的,数组a的平滑值定义为 f ( a ) m a x i 1 n − 1 ∣ a i 1 − a i ∣ f(a)max_{i1}^{n-1}|a_{i1}-a_i| f(a)maxi1n−1∣ai1−ai∣ 现在小红拿到了一个数组…...
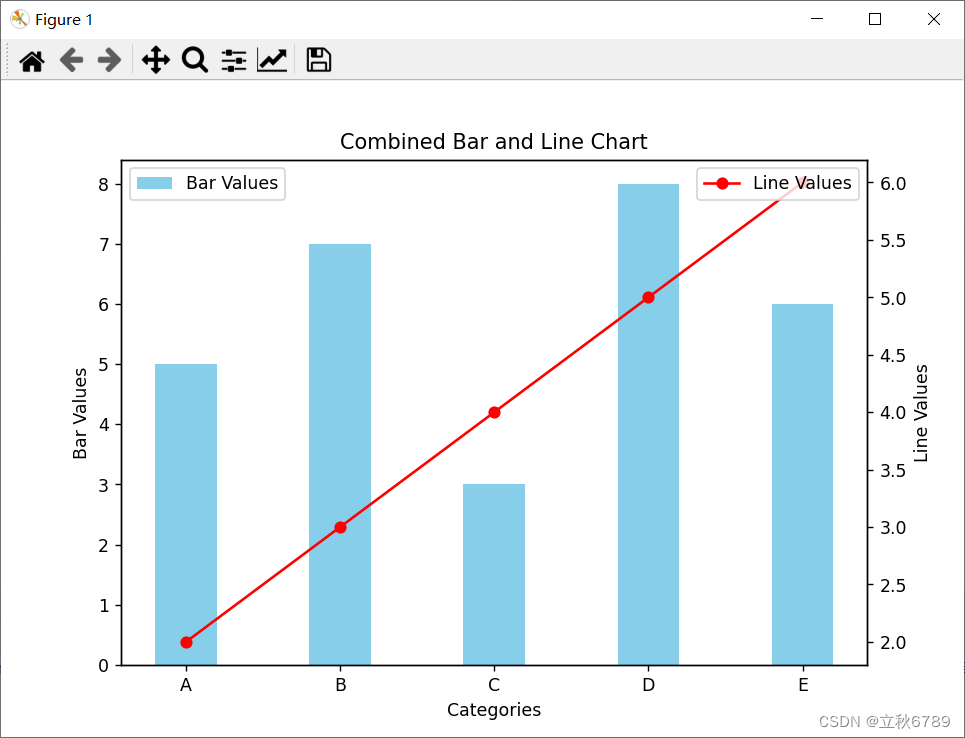
使用matplotlib绘制折线条形复合图
使用matplotlib绘制折线条形复合图 介绍效果代码 介绍 在数据可视化中,复合图形是一种非常有用的工具,可以同时显示多种数据类型的关系。在本篇博客中,我们将探讨如何使用 matplotlib 库来绘制包含折线图和条形图的复合图。 效果 代码 imp…...

云计算中网络虚拟化的核心组件——NFV、NFVO、VIM与VNF
NFV NFV(Network Functions Virtualization,网络功能虚拟化),是一种将传统电信网络中的网络节点设备功能从专用硬件中解耦并转换为软件实体的技术。通过运用虚拟化技术,NFV允许网络功能如路由器、防火墙、负载均衡器、…...

# SpringBoot 如何让指定的Bean先加载
SpringBoot 如何让指定的Bean先加载 文章目录 SpringBoot 如何让指定的Bean先加载ApplicationContextInitializer使用启动入口出注册配置文件中配置spring.factories中配置 BeanDefinitionRegistryPostProcessor使用 使用DependsOn注解实现SmartInitializingSingleton接口使用P…...

家用洗地机哪个品牌好?洗地机怎么选?这几款全网好评如潮
如今,人们家里越来越多的智能清洁家电,小到吸尘器、电动拖把,大到扫地机器人、洗地机,作为一个用过所有这些清洁工具的家庭主妇,我觉得最好用的还是洗地机。它的清洁效果比扫地机器人更好,功能也比吸尘器更…...

iOS与前端:深入解析两者之间的区别与联系
iOS与前端:深入解析两者之间的区别与联系 在数字科技高速发展的今天,iOS与前端技术作为两大热门领域,各自在移动应用与网页开发中扮演着不可或缺的角色。然而,这两者之间究竟存在哪些差异与联系呢?本文将从四个方面、…...
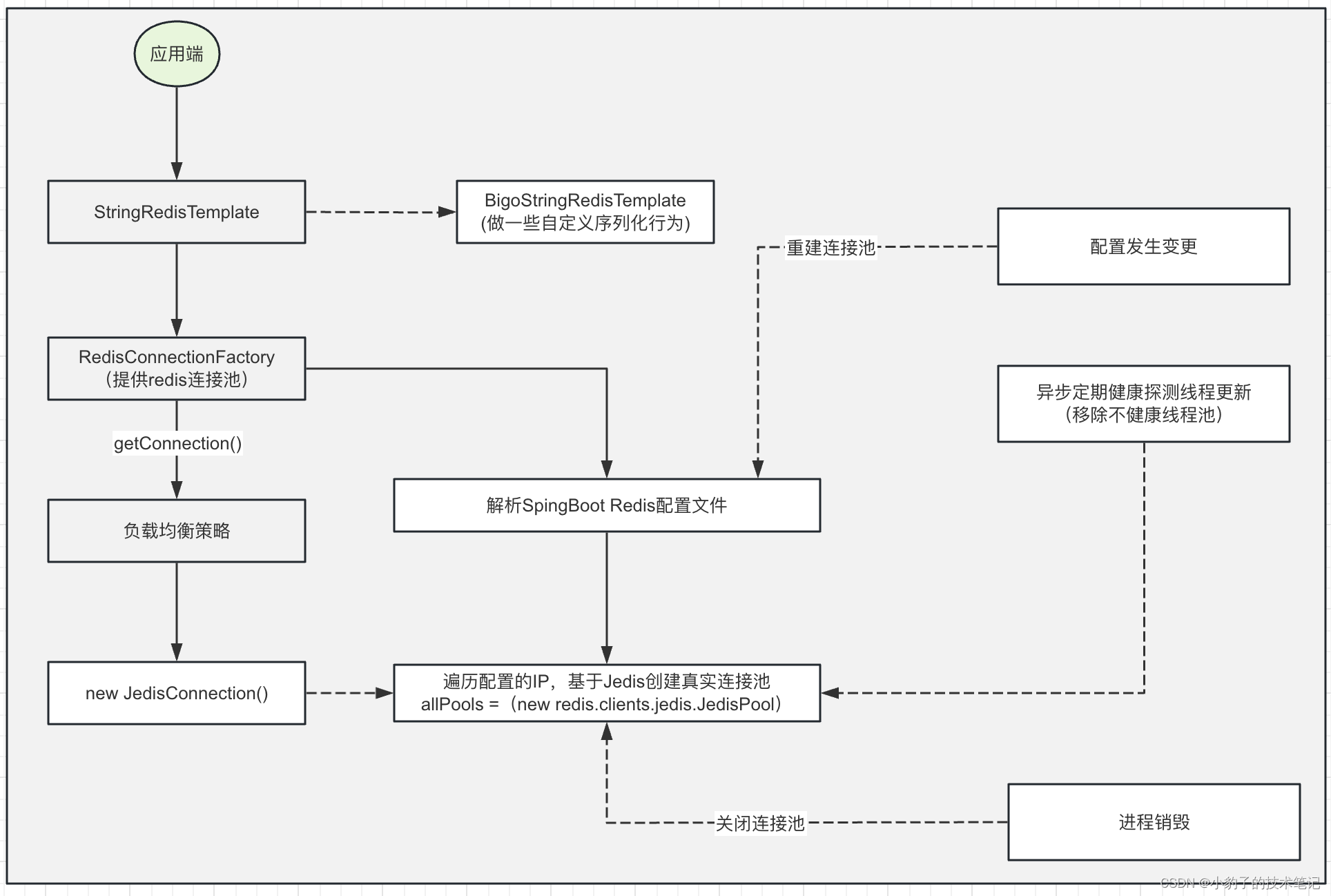
SpringBoot 基于jedis实现Codis高可用访问
codis与redis的关系 codis与redis之间关系就是codis是基于多个redis实例做了一层路由层来进行数据的路由,每个redis实例承担一定的数据分片。 codis作为开源产品,可以很直观的展示出codis运维成本低,扩容平滑最核心的优势. 其中࿰…...

力扣108. 将有序数组转换为二叉搜索树
108. 将有序数组转换为二叉搜索树 - 力扣(LeetCode) 找割点,一步一步将原数组分开。妙极了!!!!! /*** Definition for a binary tree node.* public class TreeNode {* int val;…...
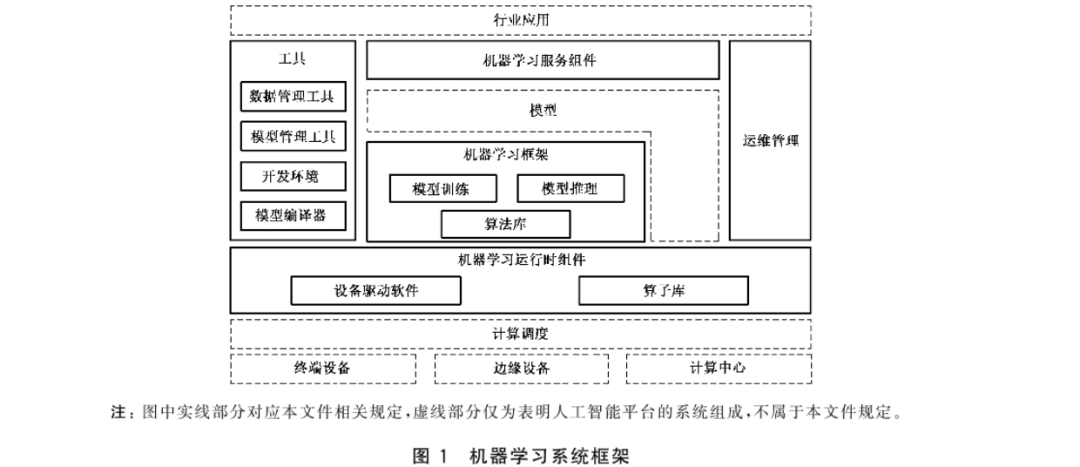
人工智能机器学习系统技术要求
一 术语和定义 1.1机器学习系统 machinelearningsystem 能运行或用于开发机器学习模型、算法和相关应用的软件系统。 1.2机器学习框架 machinelearningframework 利用预先构建和优化好的组件集合定义模型,实现对机器学习算法封装、数据调用处理和计算资源使用的软件库。 1…...

学习整理使用JavaScript中如何判断变量是否存在的四种常用方法
学习整理使用JavaScript中如何判断变量是否存在的四种常用方法 前言1. 使用 typeof 运算符判断变量类型2. 使用全局对象 window 或 global 判断变量是否存在3. 使用 in 关键字判断变量是否存在4. 使用 try…catch 块判断变量是否存在5. 综合示例总结 前言 在 JavaScript 中&am…...
docker实现jenkins+git+naocas一体化自动部署
一、jenkins安装 1.1 docker 安装jenkins docker pull jenkins/jenkins 1.2 docker 启动jenkins docker run --name myjenkins -d -p 8081:8080 -p 8085:8085 jenkins/jenkins –name 指定容器名称为myjenkins -d 表示后台运行 -p 8081:8080 表示Docker Host(运行Do…...

Flutter 中的 PerformanceOverlay 小部件:全面指南
Flutter 中的 PerformanceOverlay 小部件:全面指南 Flutter 是一个由 Google 开发的跨平台 UI 框架,它允许开发者使用 Dart 语言构建高性能、美观的应用。在 Flutter 的开发过程中,性能监控是一个重要的方面。PerformanceOverlay 是 Flutter…...
es的总结
es的collapse es的collapse只能针对一个字段聚合(针对大数据量去重),如果以age为聚合字段,则会展示第一条数据,如果需要展示多个字段,需要创建新的字段,如下 POST testleh/_update_by_query {…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...
