数据结构之归并排序算法【图文详解】

博主主页:LiUEEEEE
C语言专栏
数据结构专栏
力扣牛客经典题目专栏

目录
- 1、归并排序的基本思想
- 2、归并排序的实现
- 2.1. 归并排序的递归实现
- 2.2. 归并排序的非递归实现
- 3、归并排序非递归方法实现的常见问题
- 4、结语
1、归并排序的基本思想
归并排序的基本思想:
- 归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:

2、归并排序的实现
归并排序的实现拥有两种方法:
- 递归实现
- 非递归实现
但归根到底其主要思想不会发生变化,以下是归并排序的动态展示图:

2.1. 归并排序的递归实现
如上文所展示的效果图可知:
- 对于归并排序,需使用二叉树中后序的思想,将所给目标数组全部类二分,而后进行递归,当所递归数组个数为1时开始归并。
- 将归并后的子数组复制到原数组中对应位置,并开启新一轮的归并,这就需要我们动态开辟一个第三方数组tmp来进行辅助。
- 归并排序的递归实现代码如下所示:
void MergeSort(int* a, int* tmp, int begin, int end)
{if (begin >= end)return;int mid = (begin + end) / 2;MergeSort(a, tmp, begin, mid);MergeSort(a, tmp, mid + 1, end);int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}
2.2. 归并排序的非递归实现
其思想与递归并无差别,区别在于操作方式:
- 在递归实现中,我们使用类二分的方法将原目标数组分为2份依次进行二分的归并递归,而在非递归中,我们不再使用类二分的方法,而是直接在原数组上进行操作。
- 在逻辑上认为原数组已经进行处于递归的过程,即:令gap = 1
- 第一次对每一个元素进行归并,归并完成后,令 gap *= 2。
- 第二次对每两个元素进行归并,归并完成后,令 gap *= 2。
- …
- 第n 次对每2^(n-1)个元素进行归并,归并完成后,令 gap *= 2。
- 直到gap大于元素原本数组个数时,结束。

- 归并排序的非递归实现代码如下:
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("MergeSortNonR: malloc fail");return;}int gap = 1;while (gap < n){for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;if (begin2 >= n)对程序代码的优化,防止越界break;if (end2 >= n)对程序代码的优化,防止越界end2 = n - 1;int j = i;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2])tmp[j++] = a[begin1++];elsetmp[j++] = a[begin2++];}while (begin1 <= end1)tmp[j++] = a[begin1++];while (begin2 <= end2)tmp[j++] = a[begin2++];memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));}printf("\n");gap *= 2;}free(tmp);tmp = NULL;
}
3、归并排序非递归方法实现的常见问题
在使用非递归方法实现归并排序时,我们通常无法精确掌握其归并数组的左右区间,例如下图:

图中所展示的示例数组拥有十九个元素,但在归并过程中会发生越界行为,出现bug。
但通过途中所展示我们不难发现,出现越界的数组一般为右子数组,当右子树组的右下标出现越界时,我们可直接对其右下标进行修正即可,当右子树组的左下标越界时,就说明左子数组已经归并完成,我们可直接跳出循环进行下一次归并,直到整个数组归并完成即可。
4、结语

十分感谢您观看我的原创文章。
本文主要用于个人学习和知识分享,学习路漫漫,如有错误,感谢指正。
如需引用,注明地址。
相关文章:

数据结构之归并排序算法【图文详解】
P. S.:以下代码均在VS2019环境下测试,不代表所有编译器均可通过。 P. S.:测试代码均未展示头文件stdio.h的声明,使用时请自行添加。 博主主页:LiUEEEEE …...
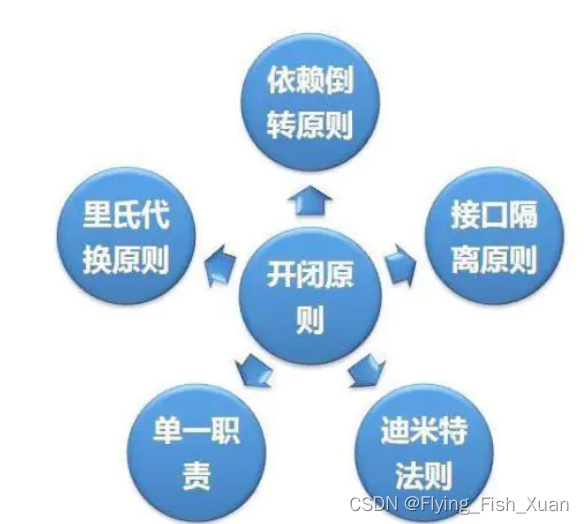
设计模式基础
什么是设计模式 设计模式是一种在软件设计过程中反复出现的问题和相应解决方案的描述。它是一种被广泛接受的经验总结,可以帮助开发人员解决常见的设计问题并提高代码的重用性、可维护性和可扩展性。 设计模式可以分为三类: 创建型模式(Crea…...

Glide支持通过url加载本地图标
序言 glide可以在load的时候传入一个资源id来加载本地图标,但是在开发过程中。还得区分数据类型来分别处理。这样的使用成本比较大。希望通过自定义ModelLoader实现通过自定义的url来加载Drawab。降低使用成本 实现 一共四个类 类名作用GlideIcon通过自定义url的…...
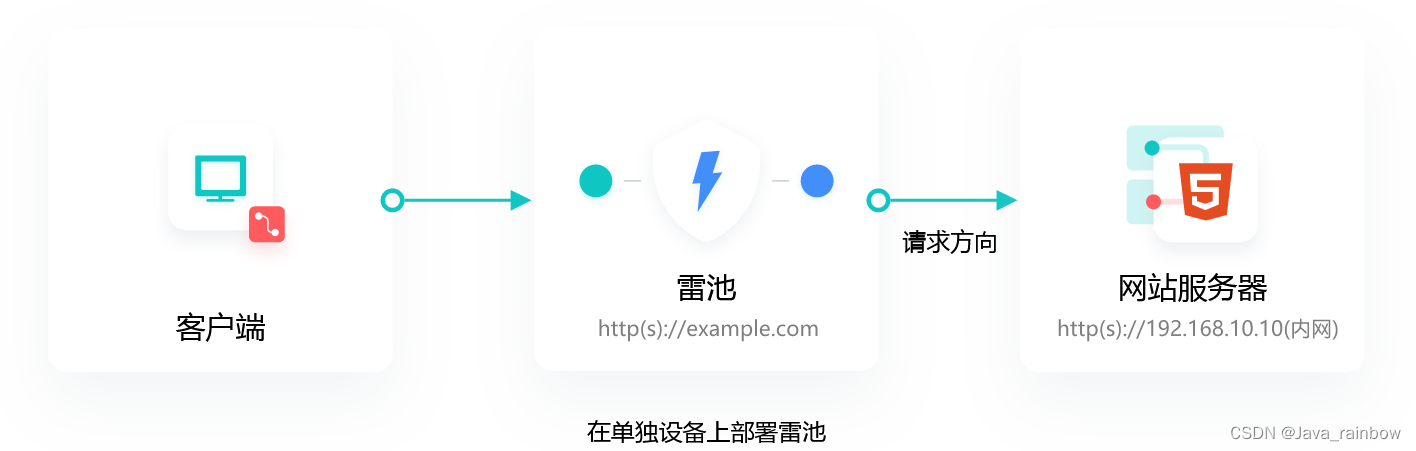
网络安全形势与WAF技术分享
我一个朋友的网站,5月份时候被攻击了,然后他找我帮忙看看,我看他的网站、网上查资料,不看不知道,一看吓一跳,最近几年这网络安全形势真是不容乐观,在网上查了一下资料,1、中国信息通…...

【实战JVM】-实战篇-06-GC调优
文章目录 1 GC调优概述1.1 调优指标1.1.1 吞吐量1.1.2 延迟1.1.3 内存使用量 2 GC调优方法2.1 发现问题2.1.1 jstat工具2.1.2 visualvm插件2.1.3 PrometheusGrafana2.1.4 GC Viewer2.1.5 GCeasy 2.2 常见GC模式2.2.1 正常情况2.2.2 缓存对象过多2.2.3 内存泄漏2.2.4 持续FullGC…...

深入解析智慧互联网医院系统源码:医院小程序开发的架构到实现
本篇文章,小编将深入解析智慧互联网医院系统的源码,重点探讨医院小程序开发的架构和实现,旨在为相关开发人员提供指导和参考。 一、架构设计 智慧互联网医院系统的架构设计是整个开发过程的核心,直接影响到系统的性能、扩展性和维…...
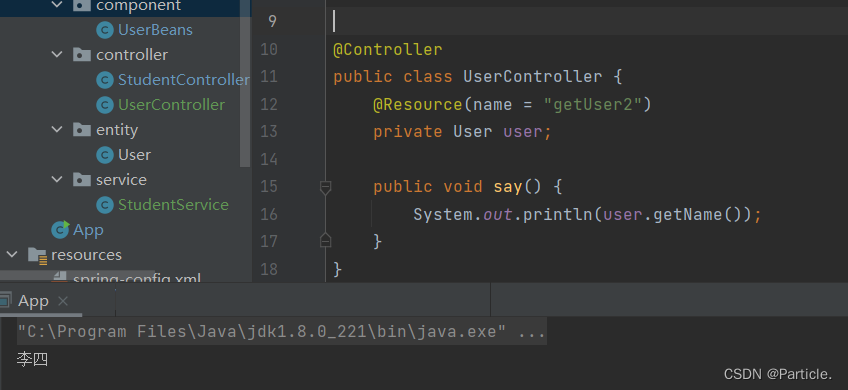
获取 Bean 对象更加简单的方式
获取 bean 对象也叫做对象装配,是把对象取出来放到某个类中,有时候也叫对象注⼊。 对象装配(对象注⼊)即DI 实现依赖注入的方式有 3 种: 1. 属性注⼊ 2. 构造⽅法注⼊ 3. Setter 注⼊ 属性注入 属性注⼊是使⽤ Auto…...

ChatGPT基本原理
技术背景与基础: 深度学习:ChatGPT建立在深度学习技术之上,通过复杂的神经网络结构模拟人类的语言处理过程。深度学习使得ChatGPT能够处理海量的文本数据,并从中提取出复杂的语言模式和规律。GPT架构:ChatGPT基于GPT&a…...

几种更新 npm 项目依赖的实用方法
几种更新 npm 项目依赖的实用方法 引言1. 使用 npm update 命令2. 使用 npm-check-updates 工具3. 使用 npm outdated 命令4. 直接手动更新 package.json 文件5. 直接安装最新版本6. 使用自动化工具结语 引言 在软件开发的过程中,我们知道依赖管理是其中一个至关重…...
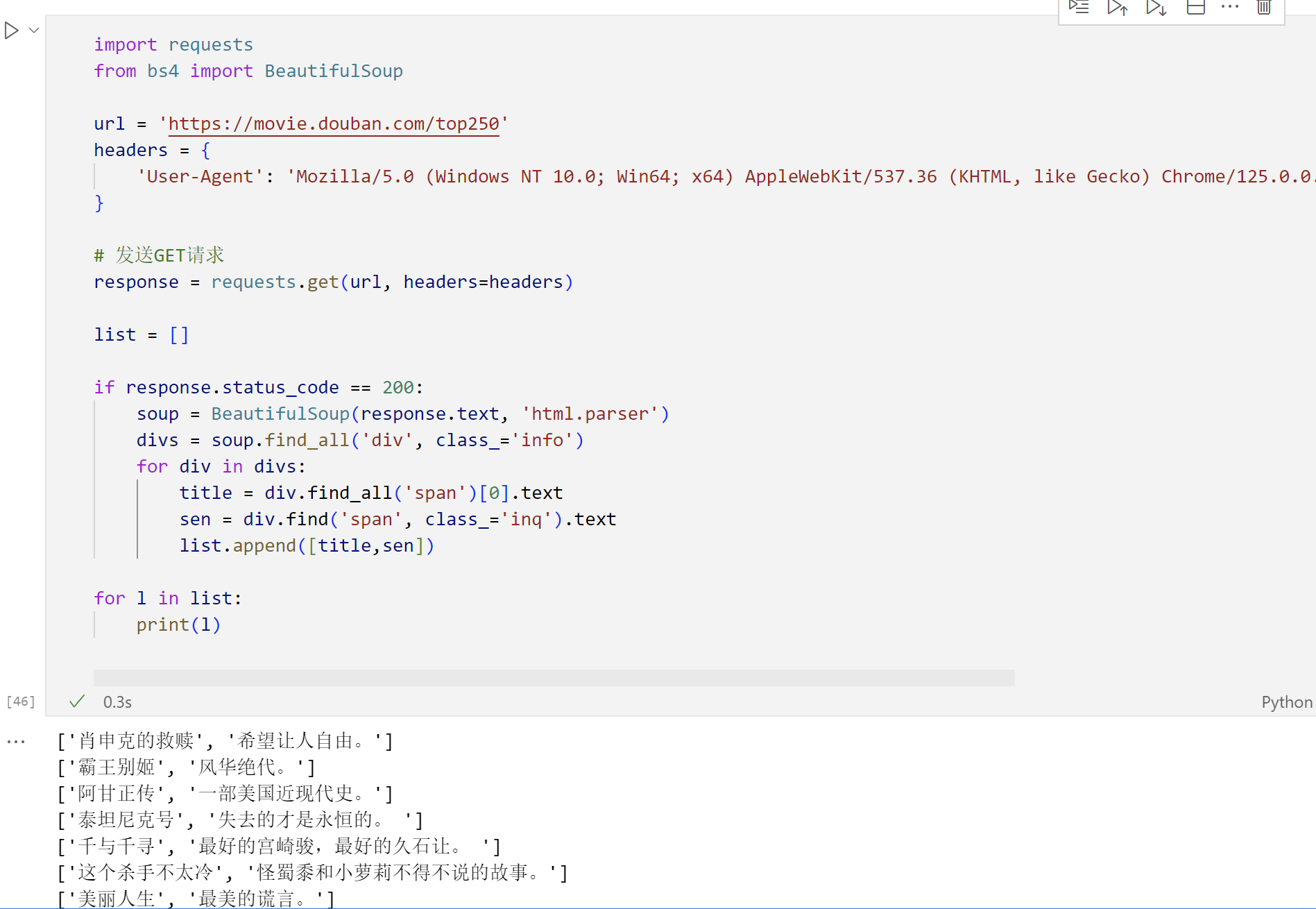
Python爬虫之简单学习BeautifulSoup库,学习获取的对象常用方法,实战豆瓣Top250
BeautifulSoup是一个非常流行的Python库,广泛应用于网络爬虫开发中,用于解析HTML和XML文档,以便于从中提取所需数据。它是进行网页内容抓取和数据挖掘的强大工具。 功能特性 易于使用: 提供简洁的API,使得即使是对网页结构不熟悉…...
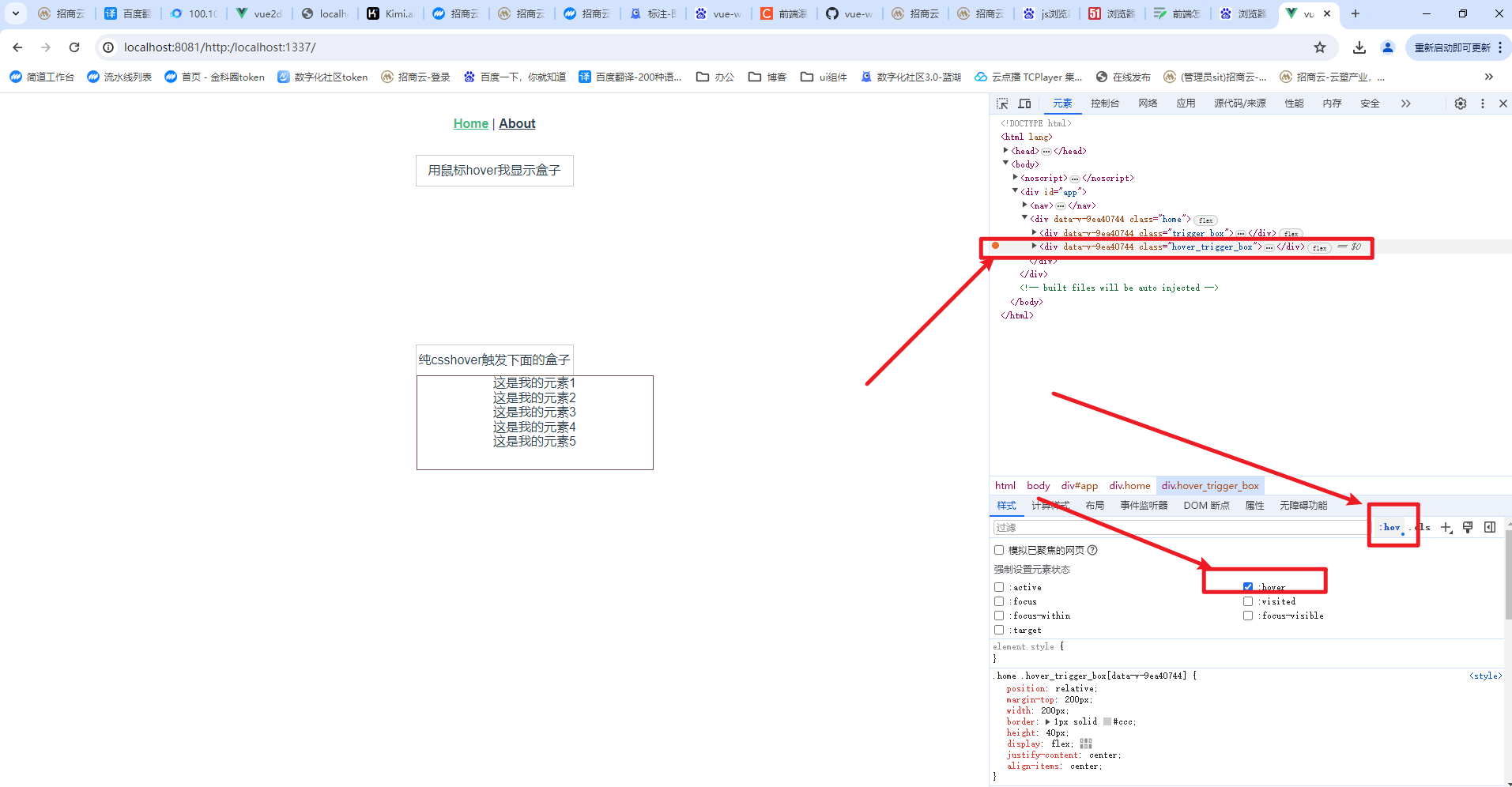
前端怎么debugger排查线上问题
前端怎么debugger排查线上问题 1.问题背景2.问题详细说明3.处理方案a.开发环境怎么找,步骤一样的:b.生产环境怎么找,步骤一样的:还有一种情况就是你的子盒子是使用csshover父盒子出来的, 4.demo地址: 1.问题…...
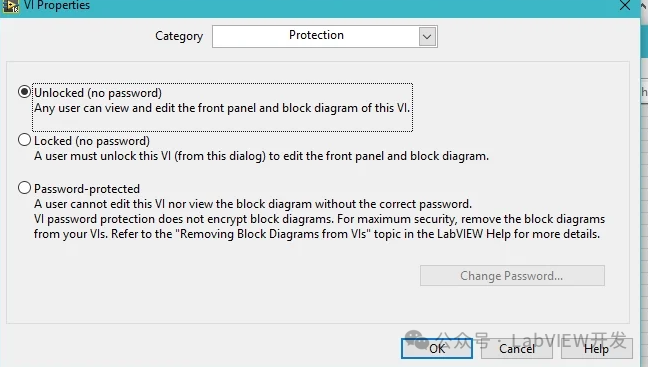
LabVIEW源程序安全性保护综合方案
LabVIEW源程序安全性保护综合方案 一、硬件加密保护方案 选择和安装硬件设备 选择加密狗和TPM设备:选择Sentinel HASP加密狗和支持TPM(可信平台模块)的计算机主板。 安装驱动和开发工具:安装Sentinel HASP加密狗的驱动程序和开发…...

JS包装类:循环中为什么建议用变量存储str.length进行循环判断?
前言 在Javascript通常我们在遍历一个字符串的时候通常使用的方式是 var str "abcdefg"; for(let i0;i<str.length;i){}但在最近的学习中,有人建议我最好应该是下面这样执行。 var str "abcdefg"; for(let i0,len str.length;i<len;i)…...
)
Android Audio实战——音量默认值修改(一)
在前面的文章《音频配置加载》中我们知道了,Audio 的一些配置信息是由硬件驱动保存到 audio_policy_configuration.xml 文件中,音量的一些默认值也会如此。但是在一些车载设备开发中,需要适配不同车型的需求,一套代码通常要适配多个车型,这就需要在 FW 层进行一些默认值的…...
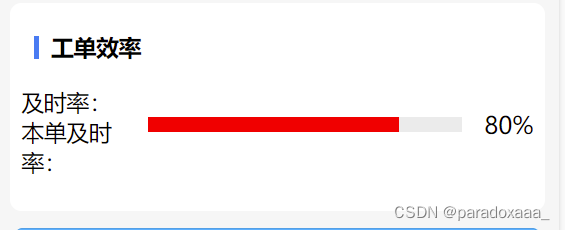
解决uni-app progress控件不显示问题
官方代码: <view class"progress-box"><progress :percent"80" show-info activeColor"red" stroke-width"10" /> </view> 进度条并不在页面中显示,那么我们需要给进度条加上宽高style"…...

使用C++版本的opencv dnn 部署onnx模型
使用OpenCV的DNN模块在C中部署ONNX模型涉及几个步骤,包括加载模型、预处理输入数据、进行推理以及处理输出。 构建了yolo类,方便调用 yolo.h 文件 #ifndef YOLO_H #define YOLO_H #include <fstream> #include <sstream> #include <io…...

python中实现队列功能
【小白从小学Python、C、Java】 【考研初试复试毕业设计】 【Python基础AI数据分析】 python中实现队列功能 选择题 以下代码最后一次输出的结果是? from collections import deque queue deque() queue.append(1) queue.append(2) queue.append(3) print(【显示】…...

自然资源-关于城镇开发边界局部优化的政策思路梳理
自然资源-关于城镇开发边界局部优化的政策思路梳理 国土空间规划的核心之一是要统筹划定“三区三线”,三条控制线中的城镇开发边界的划定与优化工作,一直是国土空间规划改革的重要组成部分,其有助于遏制城市盲目扩张,强化底线约束…...
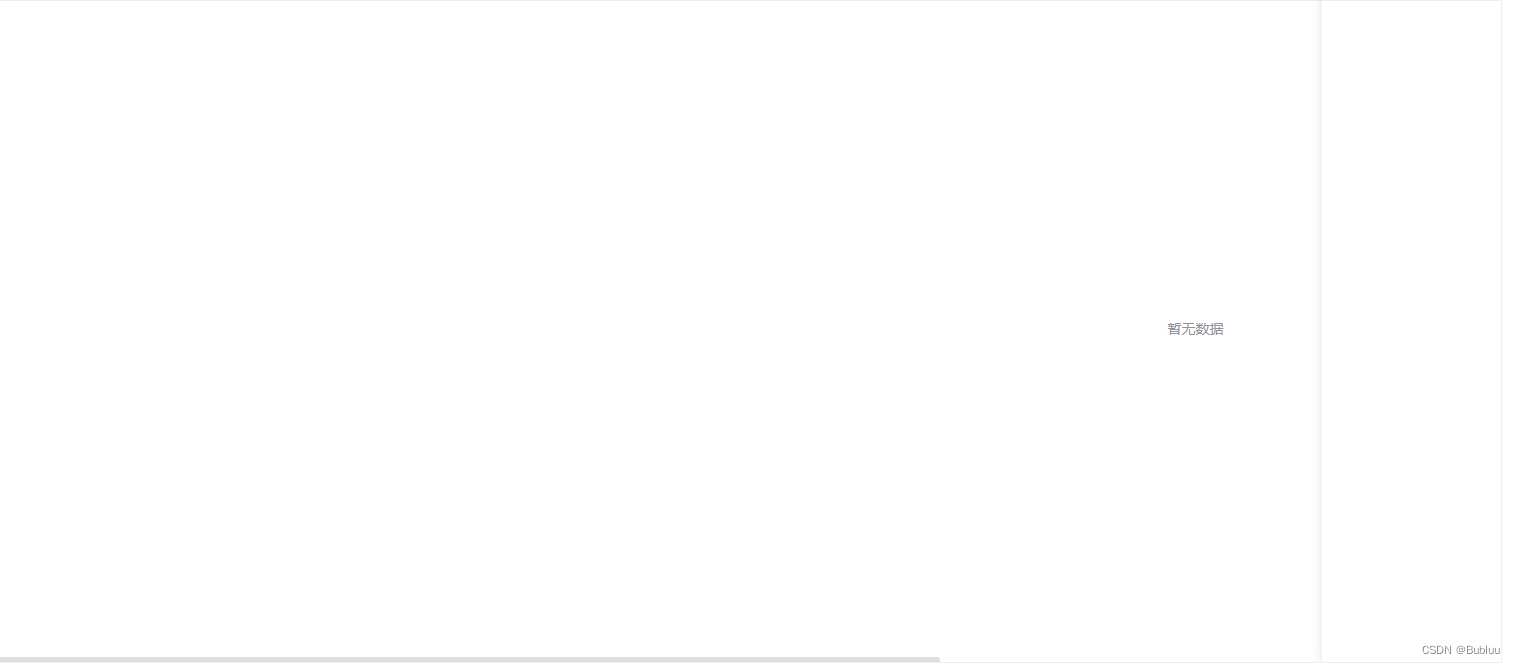
ElementUI的Table组件在无数据情况下让“暂无数据”文本居中显示
::v-deep .el-table__empty-block {width: 100%;min-width: 100%;max-width: 100%; }...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

React核心概念:State是什么?如何用useState管理组件自己的数据?
系列回顾: 在上一篇《React入门第一步》中,我们已经成功创建并运行了第一个React项目。我们学会了用Vite初始化项目,并修改了App.jsx组件,让页面显示出我们想要的文字。但是,那个页面是“死”的,它只是静态…...

echarts使用graphic强行给图增加一个边框(边框根据自己的图形大小设置)- 适用于无法使用dom的样式
pdf-lib https://blog.csdn.net/Shi_haoliu/article/details/148157624?spm1001.2014.3001.5501 为了完成在pdf中导出echarts图,如果边框加在dom上面,pdf-lib导出svg的时候并不会导出边框,所以只能在echarts图上面加边框 grid的边框是在图里…...

