Facebook的隐私保护挑战:用户数据安全的新时代
在全球范围内,Facebook已经成为了不可忽视的社交媒体巨头,它连接着超过20亿的活跃用户。然而,随着其影响力的不断扩大,关于用户隐私和数据安全的问题也愈加引人关注。本文将深入探讨Facebook面临的隐私保护挑战,以及它在用户数据安全方面所采取的措施和未来展望。
1. 数据隐私的历史问题
Facebook的隐私问题可以追溯到其成立初期。在2004年创立之初,Facebook主要面对大学生用户,因此隐私问题并没有被广泛关注。然而,随着用户群体的不断扩大,隐私问题逐渐浮出水面。2018年的剑桥分析数据丑闻是Facebook隐私保护历史上的一个重要转折点,该事件涉及8700万用户的数据泄露,并对全球政治选举产生了深远影响。这一事件不仅引发了公众的愤怒,也促使全球各地的监管机构对Facebook展开了深入调查。
2. 监管压力与法律挑战
随着隐私问题的持续发酵,全球各地的政府和监管机构也开始加大对Facebook的监管力度。欧盟于2018年出台的《通用数据保护条例》(GDPR),为用户数据保护设立了严格的标准,Facebook因此受到巨大压力。美国的《加利福尼亚消费者隐私法案》(CCPA)也对Facebook的隐私保护提出了新的要求。这些法律法规要求Facebook在数据收集、存储和使用方面更加透明,并给予用户更多的控制权。
3. Facebook的隐私保护措施
面对巨大的舆论压力和法律挑战,Facebook采取了一系列措施来增强用户数据的隐私保护。以下是一些重要的举措:
隐私控制工具:增强隐私保护:
IPRockets提供的高效代理服务可以进一步保护用户的隐私。通过使用IPRockets的代理,用户的真实IP地址可以被隐藏,从而避免在访问Facebook时暴露其真实位置和身份信息。这为用户提供了一个额外的隐私保护层,尤其在需要匿名浏览或防止追踪的情况下更为重要。
数据透明度:Facebook增加了数据透明度,向用户提供关于其数据如何被收集和使用的详细信息。通过“访问你的信息”工具,用户可以查看和下载他们在Facebook上的所有数据。
安全措施:Facebook不断加强其平台的安全措施,包括引入双因素认证、防止未经授权的访问和数据泄露,以及使用高级加密技术来保护用户数据。
4. 面临的持续挑战
尽管Facebook在隐私保护方面做出了许多努力,但它仍然面临诸多挑战。首先是技术上的挑战,随着数据分析和人工智能技术的进步,保护用户隐私变得越来越复杂。其次是信任问题,剑桥分析事件之后,许多用户对Facebook的信任度大大降低,恢复公众信任需要时间和持续的努力。此外,全球各地的法律法规不断变化,Facebook需要不断调整其政策和实践,以符合不同地区的监管要求。
5. 未来展望
未来,Facebook在隐私保护方面需要继续努力,以应对不断变化的技术和法规环境。首先,Facebook需要进一步提升其隐私保护技术,特别是在数据加密、匿名化和数据分割等方面。此外,Facebook还需要加强与用户的沟通,透明地向用户展示其隐私保护措施和数据使用情况,以重建用户的信任。最后,Facebook应积极参与全球隐私保护政策的制定,与各国监管机构合作,共同推动用户隐私保护水平的提升。
结语
在数据驱动的数字时代,隐私保护已成为社交媒体平台面临的重大挑战。Facebook作为全球最大的社交媒体平台之一,必须承担起保护用户数据安全的责任。通过不断完善隐私保护措施,增强数据透明度,并积极应对技术和法规挑战,Facebook有望在用户数据安全的新时代中继续发挥重要作用,为用户提供更加安全和可靠的社交体验。
相关文章:

Facebook的隐私保护挑战:用户数据安全的新时代
在全球范围内,Facebook已经成为了不可忽视的社交媒体巨头,它连接着超过20亿的活跃用户。然而,随着其影响力的不断扩大,关于用户隐私和数据安全的问题也愈加引人关注。本文将深入探讨Facebook面临的隐私保护挑战,以及它…...
Gradio.NET:一个快速制作演示demo网页的利器
Gradio介绍 Gradio是一个用于创建机器学习模型交互界面的Python库。它允许开发者快速为他们的模型创建一个简单的web界面,以便于非技术用户和其他开发者进行交互和测试。 Gradio的主要优点是易用性和灵活性。你只需要几行代码就可以为你的模型创建一个交互界面。你…...
)
001 IOC与DI(有点杂)
文章目录 IOC与DI区别联系总结 依赖注入解耦管理对象的生命周期提高配置灵活性三种注入方式不可变对象的设计 构造器注入Setter方法注入字段注入Setter方法注入为什么不破坏封装性字段注入为什么破坏封装性为什么将字段或setter方法设置为private?总结 setter方法注…...

Python语言自学:深入探索四个基础、五个进阶、六个实战及七个挑战
Python语言自学:深入探索四个基础、五个进阶、六个实战及七个挑战 Python,作为一种通用编程语言,其简洁的语法、丰富的库和强大的功能,使得越来越多的人选择自学Python。但自学之路并非坦途,本文将从四个方面、五个方…...

运维开发介绍
目录 1.什么是运维开发 2.作用 3.优点 4.缺点 5.应用场景 5.1.十个应用场景 5.2.网站和Web应用程序 6.案例 7.小结 1.什么是运维开发 运维开发(DevOps)是一种结合软件开发(Development)与信息技术运维(Opera…...

Mac版的Typora的安装和激活(亲测可用哦~~~)
星光下的赶路人star的个人主页 珍视生活中的苦与乐,悦纳生活的悲伤离合 文章目录 1.下载2.安装3.激活4.注意点 1.下载 直接官网下载即可!!! 官网地址:typora官网 2.安装 直接拖进去安装即可 3.激活 1.利用访达进入…...

【Python系列】Python 方法变量参数详解
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...
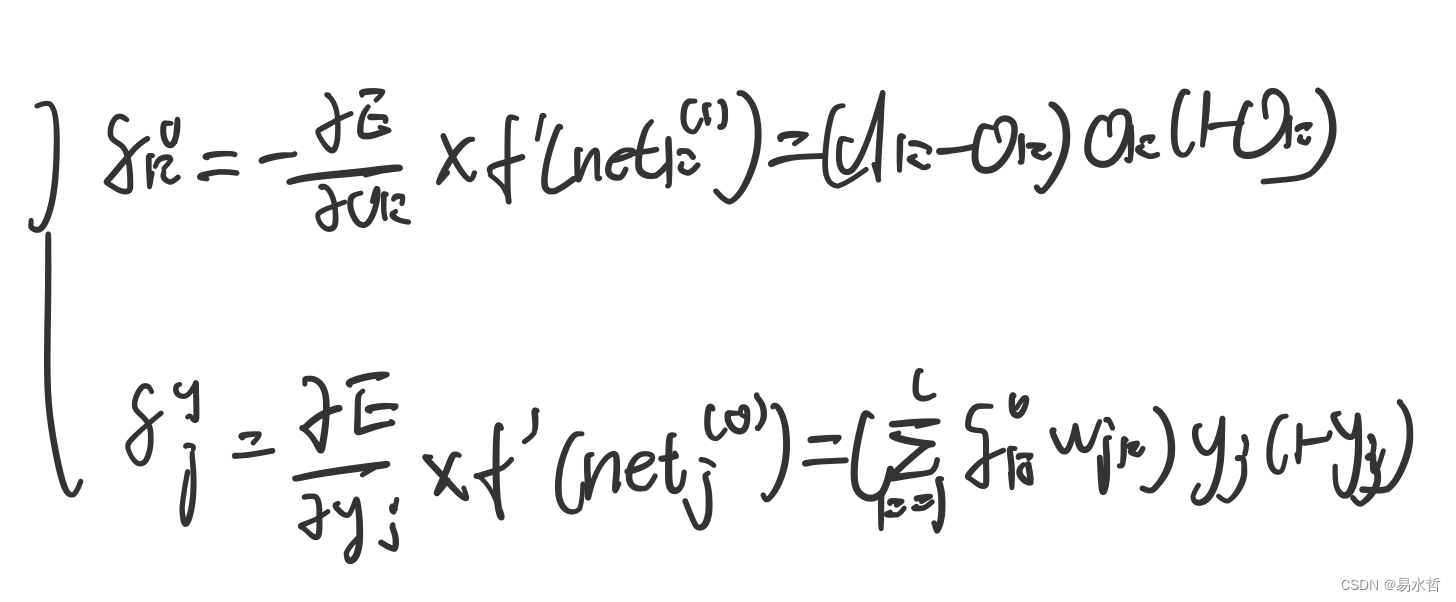
生命在于学习——Python人工智能原理(3.2)
三、深度学习 (二)人工神经网络 人工神经网络是模仿人类大脑神经系统工作原理所创建的数学模型,有并行的分布处理能力、高容错性和自我学习等特征。 1、感知器 感知器由Frank Roseblatt于1957年提出,是一种广泛使用的线性分类…...

JAVA面试八股文----Mybatis
1、Mybatis 1.1#{}和${}的区别是什么? Mybatis在处理#{}时,会将sql中的#{}替换为?号,调用PreparedStatement的set方法来赋值; Mybatis在处理 0 时,就是把 0时,就是把 0时,就是把{}替换成变量的值。 有了#{}为什么还需要${}? #{}会被预编译处理,可以有效的防止SQL注…...
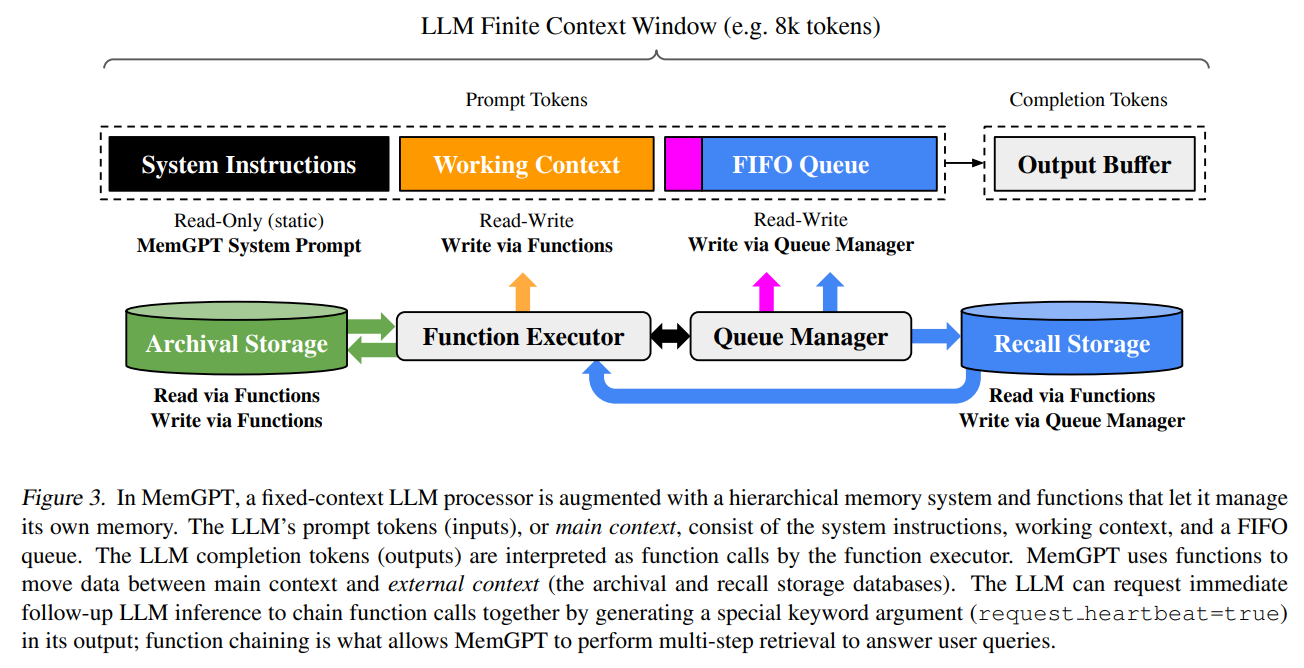
[论文笔记]MemGPT: Towards LLMs as Operating Systems
引言 今天介绍一篇论文MemGPT: Towards LLMs as Operating Systems。翻过过来就是把LLM看成操作系统。 大语言模型已经在人工智能领域引起了革命性的变革,但受到有限上下文窗口的限制,在扩展对话和文档分析等任务中的效用受到了阻碍。为了能够利用超出…...

Sentinel1.8.6更改配置同步到nacos(项目是Gateway)
本次修改的源码在:https://gitee.com/stonic-open-source/sentinel-parent 一 下载源码 地址:https://github.com/alibaba/Sentinel/releases/tag/1.8.6 二 导入idea,等待maven下载好各种依赖 三 打开sentile-dashboard这个模块…...

材料科学领域科技查新点提炼方法!---附案例
材料科学是研究材料的组织结构、性质、生产流程、使用效能及它们之间的相互关系的科学,集物理学、化学、冶金学等于一体。随着科技的发展,纳米技术和生物技术也广泛应用到该领域中。从材质上可以分为金属材料、无机非金属材料、有机高分子材料和复合材料…...

深入理解HTTP与TCP:应用层与传输层的区分
一、前言 在互联网协议栈中,应用层和传输层是两个重要的层级,分别承载了不同的功能。HTTP(HyperText Transfer Protocol)作为应用层协议,而TCP(Transmission Control Protocol)则是传输层协议&…...

Unity3D Delaunay德罗内三角算法详解
Unity3D是一款强大的游戏开发引擎,它提供了丰富的功能和工具,使开发者能够轻松创建出色的游戏和应用程序。其中,Delaunay德罗内三角算法是一种常用的计算几何算法,用于生成三角形网格,其在Unity3D中的应用也非常广泛。…...
JAVA小案例-输出100-150中能被3整除的数,每5个换行
JAVA小案例-输出100-150中能被3整除的数,每5个换行 代码如下: public class Continue {/*** continue练习,输出100-150中能被3整除的数,每5个换行* param args*/public static void main(String[] args) {int count 0;//计数器…...

论程序员的职业素养
文章目录 前言一、命名规范1. HTML命名规范2. CSS命名规范3. JavaScript命名规范4. 文件和文件夹命名规范5. 代码案例 二、代码注释规范1. 注释规范2. 案例代码HTMLCSS (styles/main.css)JavaScript (scripts/main.js) 三、代码逻辑规范1.逻辑规范2. 代码案例清晰的函数和模块化…...

前端canvas绘图,利用canvas在图片上面绘制标记以及给canvas添加点击事件。
前端canvas绘图,利用canvas在图片上面绘制标记以及给canvas添加点击事件。 需要实现的效果如下图: 首先需要一个承载的核心画布 <canvas id"canvas" width"800" height"600"></canvas>全部代码: <!DOCT…...

38、Flink 的 WindowAssigner 之 GlobalWindows 示例
1、注意 使用 GlobalWindows 需要自定义 Trigger,否则窗口中的数据不会被计算。 2、代码示例 import org.apache.flink.streaming.api.datastream.DataStreamSource; import org.apache.flink.streaming.api.environment.StreamExecutionEnvironment; import org…...

同事仅靠着自己写的npm包跳槽去了大厂,羡慕了一整天
同事们之间总会悄悄聊一些话题,比如聊一些八卦啦,聊一些领导啦,也会偶尔说想跳槽,但这年头,跳槽多费劲啊,谁没事敢动。还别说,边上做了个同事,前两天还真要撤了,聊了半天…...

Yocto - bitbake任务中clean和cleanall的区别
在 BitBake 中,clean 和 cleanall 命令都用于删除构建工件,但它们的范围和执行的清理程度不同。 1. clean 命令: 目的:clean命令用于删除与特定任务或配方相关的临时构建文件和工件。 范围:它只清除指定任务或配方生…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

基于stm32F10x 系列微控制器的智能电子琴(附完整项目源码、详细接线及讲解视频)
注:文章末尾网盘链接中自取成品使用演示视频、项目源码、项目文档 所用硬件:STM32F103C8T6、无源蜂鸣器、44矩阵键盘、flash存储模块、OLED显示屏、RGB三色灯、面包板、杜邦线、usb转ttl串口 stm32f103c8t6 面包板 …...
