Unity3D Delaunay德罗内三角算法详解
Unity3D是一款强大的游戏开发引擎,它提供了丰富的功能和工具,使开发者能够轻松创建出色的游戏和应用程序。其中,Delaunay德罗内三角算法是一种常用的计算几何算法,用于生成三角形网格,其在Unity3D中的应用也非常广泛。本文将详细介绍Unity3D中Delaunay德罗内三角算法的原理和实现,并给出相应的代码示例。
对惹,这里有一个游戏开发交流小组,希望大家可以点击进来一起交流一下开发经验呀!
一、Delaunay德罗内三角算法原理
Delaunay德罗内三角算法是一种用于生成三角形网格的算法,其主要思想是在给定一组点的情况下,构建一个不包含任何点在其内部的三角形网格。在这个三角形网格中,任意两个三角形之间都满足德罗内圆空间最小原则,即对于任意两个相邻的三角形,其外接圆不包含任何其他点。
Delaunay德罗内三角算法的基本步骤如下:
- 初始化:将所有点按照一定规则放入一个初始三角形中。
- 逐点插入:依次将每个点插入到当前三角形网格中。
- 修正:对于每个插入的点,根据德罗内圆空间最小原则,修正相邻的三角形。
- 输出:生成最终的三角形网格。
二、Delaunay德罗内三角算法实现
在Unity3D中,可以使用C#语言来实现Delaunay德罗内三角算法。以下是一个简单的代码示例,用于在Unity3D中生成Delaunay三角形网格:
using System.Collections;
using System.Collections.Generic;
using UnityEngine;public class DelaunayTriangulation : MonoBehaviour
{public List<Vector2> points;void Start(){// 初始化点集points = new List<Vector2>();points.Add(new Vector2(0, 0));points.Add(new Vector2(1, 0));points.Add(new Vector2(0.5f, Mathf.Sqrt(3) / 2));// 生成Delaunay三角形网格List<Triangle> triangles = Triangulate(points);}// 生成Delaunay三角形网格List<Triangle> Triangulate(List<Vector2> points){List<Triangle> triangles = new List<Triangle>();// 创建一个超级三角形包围所有点float minX = points[0].x;float minY = points[0].y;float maxX = points[0].x;float maxY = points[0].y;for (int i = 1; i < points.Count; i++){if (points[i].x < minX) minX = points[i].x;if (points[i].y < minY) minY = points[i].y;if (points[i].x > maxX) maxX = points[i].x;if (points[i].y > maxY) maxY = points[i].y;}float dx = maxX - minX;float dy = maxY - minY;float deltaMax = Mathf.Max(dx, dy);float midx = (minX + maxX) / 2;float midy = (minY + maxY) / 2;Vector2 p1 = new Vector2(midx - 20 * deltaMax, midy - deltaMax);Vector2 p2 = new Vector2(midx, midy + 20 * deltaMax);Vector2 p3 = new Vector2(midx + 20 * deltaMax, midy - deltaMax);triangles.Add(new Triangle(p1, p2, p3));// 逐点插入for (int i = 0; i < points.Count; i++){List<Triangle> badTriangles = new List<Triangle>();List<Edge> polygon = new List<Edge>();for (int j = triangles.Count - 1; j >= 0; j--){if (triangles[j].CircumcircleContains(points[i])){badTriangles.Add(triangles[j]);polygon.Add(triangles[j].edge1);polygon.Add(triangles[j].edge2);polygon.Add(triangles[j].edge3);triangles.RemoveAt(j);}}List<Edge> boundary = new List<Edge>();for (int j = polygon.Count - 1; j >= 0; j--){if (polygon.FindAll(x => x.Equals(polygon[j])).Count == 1){boundary.Add(polygon[j]);}}for (int j = boundary.Count - 1; j >= 0; j--){triangles.Add(new Triangle(boundary[j].p1, boundary[j].p2, points[i]));}}// 移除超级三角形for (int i = triangles.Count - 1; i >= 0; i--){if (triangles[i].ContainsVertex(p1) || triangles[i].ContainsVertex(p2) || triangles[i].ContainsVertex(p3)){triangles.RemoveAt(i);}}return triangles;}
}public class Triangle
{public Vector2 p1, p2, p3;public Edge edge1, edge2, edge3;public Triangle(Vector2 p1, Vector2 p2, Vector2 p3){this.p1 = p1;this.p2 = p2;this.p3 = p3;edge1 = new Edge(p1, p2);edge2 = new Edge(p2, p3);edge3 = new Edge(p3, p1);}public bool ContainsVertex(Vector2 point){return point == p1 || point == p2 || point == p3;}public bool CircumcircleContains(Vector2 point){float ax = p1.x - point.x;float ay = p1.y - point.y;float bx = p2.x - point.x;float by = p2.y - point.y;float cx = p3.x - point.x;float cy = p3.y - point.y;float ab = ax * (p1.x + point.x) + ay * (p1.y + point.y);float bc = bx * (p2.x + point.x) + by * (p2.y + point.y);float ca = cx * (p3.x + point.x) + cy * (p3.y + point.y);float circumcircle = ax * (by * ca - bc * cy) - bx * (ay * ca - ab * cy) + cx * (ay * bc - ab * by);return circumcircle > 0;}
}public class Edge
{public Vector2 p1, p2;public Edge(Vector2 p1, Vector2 p2){this.p1 = p1;this.p2 = p2;}public bool Equals(Edge other){return (p1 == other.p1 && p2 == other.p2) || (p1 == other.p2 && p2 == other.p1);}
}在上面的代码示例中,首先定义了一个DelaunayTriangulation类,其中包含了Triangulate方法用于生成Delaunay三角形网格。在Triangulate方法中,首先创建一个超级三角形包围所有点,然后逐点插入,修正相邻的三角形,并最终生成最终的三角形网格。Triangle和Edge类分别用于表示三角形和边,其中包含了一些辅助方法用于判断点是否在三角形内部和计算德罗内圆。
三、总结
通过本文的介绍,我们了解了Unity3D中Delaunay德罗内三角算法的原理和实现方法。Delaunay德罗内三角算法是一种常用的计算几何算法,用于生成三角形网格。在Unity3D中,我们可以使用C#语言来实现Delaunay德罗内三角算法,并生成漂亮的三角形网格。希望本文对你有所帮助,谢谢阅读!
相关文章:

Unity3D Delaunay德罗内三角算法详解
Unity3D是一款强大的游戏开发引擎,它提供了丰富的功能和工具,使开发者能够轻松创建出色的游戏和应用程序。其中,Delaunay德罗内三角算法是一种常用的计算几何算法,用于生成三角形网格,其在Unity3D中的应用也非常广泛。…...
JAVA小案例-输出100-150中能被3整除的数,每5个换行
JAVA小案例-输出100-150中能被3整除的数,每5个换行 代码如下: public class Continue {/*** continue练习,输出100-150中能被3整除的数,每5个换行* param args*/public static void main(String[] args) {int count 0;//计数器…...

论程序员的职业素养
文章目录 前言一、命名规范1. HTML命名规范2. CSS命名规范3. JavaScript命名规范4. 文件和文件夹命名规范5. 代码案例 二、代码注释规范1. 注释规范2. 案例代码HTMLCSS (styles/main.css)JavaScript (scripts/main.js) 三、代码逻辑规范1.逻辑规范2. 代码案例清晰的函数和模块化…...

前端canvas绘图,利用canvas在图片上面绘制标记以及给canvas添加点击事件。
前端canvas绘图,利用canvas在图片上面绘制标记以及给canvas添加点击事件。 需要实现的效果如下图: 首先需要一个承载的核心画布 <canvas id"canvas" width"800" height"600"></canvas>全部代码: <!DOCT…...

38、Flink 的 WindowAssigner 之 GlobalWindows 示例
1、注意 使用 GlobalWindows 需要自定义 Trigger,否则窗口中的数据不会被计算。 2、代码示例 import org.apache.flink.streaming.api.datastream.DataStreamSource; import org.apache.flink.streaming.api.environment.StreamExecutionEnvironment; import org…...

同事仅靠着自己写的npm包跳槽去了大厂,羡慕了一整天
同事们之间总会悄悄聊一些话题,比如聊一些八卦啦,聊一些领导啦,也会偶尔说想跳槽,但这年头,跳槽多费劲啊,谁没事敢动。还别说,边上做了个同事,前两天还真要撤了,聊了半天…...

Yocto - bitbake任务中clean和cleanall的区别
在 BitBake 中,clean 和 cleanall 命令都用于删除构建工件,但它们的范围和执行的清理程度不同。 1. clean 命令: 目的:clean命令用于删除与特定任务或配方相关的临时构建文件和工件。 范围:它只清除指定任务或配方生…...
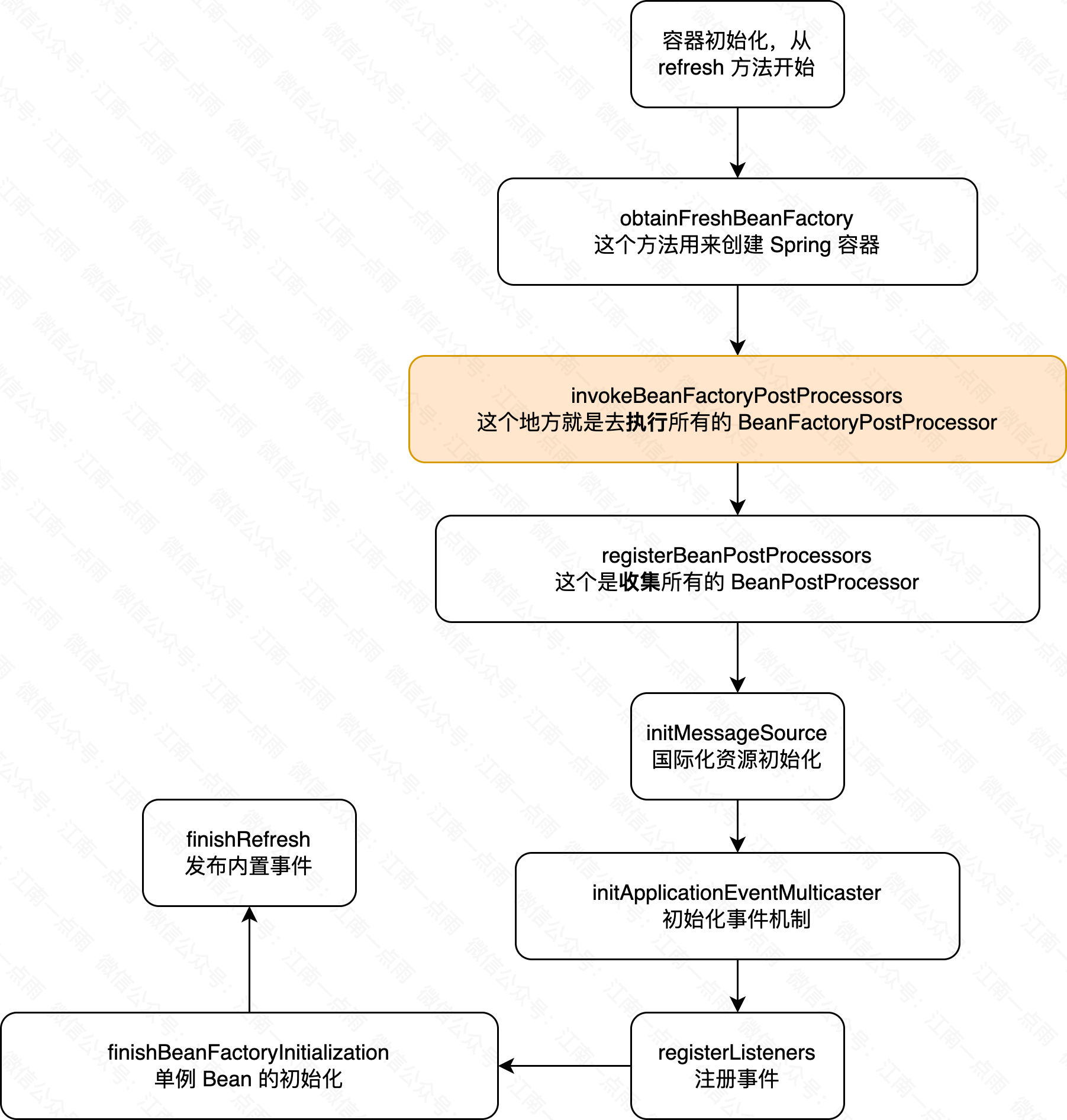
Spring 中如何控制 Bean 的加载顺序?
如果你脱口而出说添加 Order 注解或者是实现 Ordered 接口,那么恭喜,你掉坑了。 一 Order 注解和 Ordered 接口 在 Spring 框架中,Order 是一个非常实用的元注解,它位于 spring-core 包下,主要用于控制某些特定上下文…...
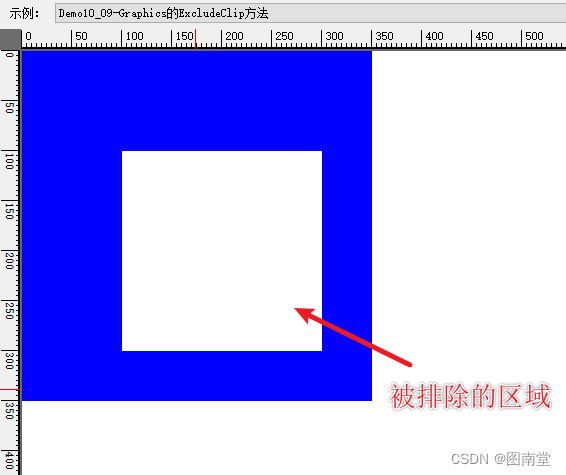
【学习笔记】Windows GDI绘图(十)Graphics详解(中)
文章目录 Graphics的方法AddMetafileComment添加注释BeginContainer和EndContainer新建、还原图形容器不指定指定源与目标矩形指定源与目标矩形 Clear清空并填充指定颜色CopyFromScreen截图CopyPixelOperation DrawImage绘制图像DrawImage的GraphicsDrawImageAbort回调ExcludeC…...

web学习笔记(六十二)
目录 1.键盘事件 2.KeepAlive 3.组件传值 3.1 兄弟组件传值 3.2 组件树传值 3.3 发布订阅者传值 1.键盘事件 keydown表示键盘事件,在不加修饰符的情况下,点击键盘上的任意位置都可以触发键盘事件, <template><div><!--…...

每天CTF小练一点--ctfshow年CTF
初一 题目: 2023是兔年,密码也是。聪明的小伙伴们,你能破解出下面的密码吗? 感谢大菜鸡师傅出题 flag格式是ctfshow{xxxxxx}.或许密码也有密码。 密文是: U2FsdGVkX1M7duRffUvQgJlESPfOTV2i4TJpc9YybgZ9ONmPk/RJje …...

Java Set接口 - TreeSet类
TreeSet 是 Java 集合框架中的一个类,它实现了 NavigableSet 接口,而 NavigableSet 是 SortedSet 接口的一个子接口。TreeSet 基于红黑树(一种自平衡的二叉搜索树)实现,因此它可以保证集合中的元素以升序排列。 以下是…...

css 理解了原理,绘制三角形就简单了
1.border-位置 注意:border-bottom/up/right/left 主要是以三角形的结构搭建而成,而border也是如此。而且从边框的外围开始计算像素尺寸。在理解了这一点之后,绘制三角形就简单多了。 1.transparent 注意:该属性主要是颜色透明…...

【JavaEE进阶】——MyBatis操作数据库 (#{}与${} 以及 动态SQL)
目录 🚩#{}和${} 🎈#{} 和 ${}区别 🎈${}使用场景 📝排序功能 📝like 查询 🚩数据库连接池 🎈数据库连接池使⽤ 🚩MySQL开发企业规范 🚩动态sql 🎈…...
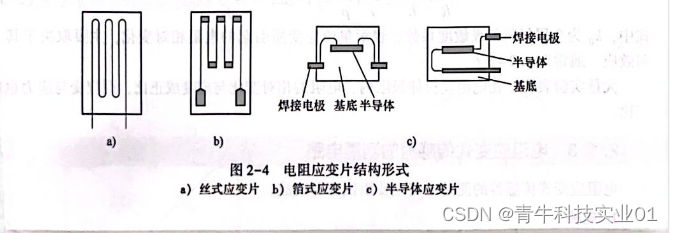
电阻应变片的结构
电阻应变片的结构 常用的电阻应变片有金属应变片和半导体应变片两种。金属应变片分为体型和薄膜型。半导体应变片常见的有体型、薄膜型、扩散型、外延型、PN结及其他形式。图2—2所示为工程常见的应变片实物。 电阻应变片的典型结构如图2—3所示。它由敏感栅、基底、覆盖层和引…...

云原生时代:从 Jenkins 到 Argo Workflows,构建高效 CI Pipeline
作者:蔡靖 Argo Workflows Argo Workflows [ 1] 是用于在 Kubernetes 上编排 Job 的开源的云原生工作流引擎。可以轻松自动化和管理 Kubernetes 上的复杂工作流程。适用于各种场景,包括定时任务、机器学习、ETL 和数据分析、模型训练、数据流 pipline、…...

【数据库系统概论】事务
概述 在数据库系统中,事务(Transaction)是指一组作为单个逻辑工作单元执行的操作。这些操作要么全部成功(提交),要么全部失败(回滚)。事务的主要目的是确保数据库的完整性和一致性&…...
C++-排序算法详解
目录 一. 冒泡排序: 二. 插入排序: 三. 快速排序: 四. 选择排序 五, 归并排序 六, 堆排序. 排序算法是一种将一组数据按照特定顺序(如升序或降序)进行排列的算法。 其主要目的是对一组无序的数据进行整理&#…...
)
Kotlin 引用(双冒号::)
文章目录 双冒号::引用函数普通函数成员函数类构造函数 引用变量(很少用)普通变量成员变量 双冒号:: Kotlin 中可以使用双冒号::对某一变量、函数进行引用。 Note:MyClass::class可用于获取KClass<MyClass>,此时的双冒号::…...
C++ day3练习
设计一个Per类,类中包含私有成员:姓名、年龄、指针成员身高、体重,再设计一个Stu类,类中包含私有成员:成绩、Per类对象p1,设计这两个类的构造函数、析构函数。 #include <iostream>using namespace std;class Per{private:…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

Qt的学习(一)
1.什么是Qt Qt特指用来进行桌面应用开发(电脑上写的程序)涉及到的一套技术Qt无法开发网页前端,也不能开发移动应用。 客户端开发的重要任务:编写和用户交互的界面。一般来说和用户交互的界面,有两种典型风格&…...

二叉树-144.二叉树的前序遍历-力扣(LeetCode)
一、题目解析 对于递归方法的前序遍历十分简单,但对于一位合格的程序猿而言,需要掌握将递归转化为非递归的能力,毕竟递归调用的时候会调用大量的栈帧,存在栈溢出风险。 二、算法原理 递归调用本质是系统建立栈帧,而非…...

【Pandas】pandas DataFrame dropna
Pandas2.2 DataFrame Missing data handling 方法描述DataFrame.fillna([value, method, axis, …])用于填充 DataFrame 中的缺失值(NaN)DataFrame.backfill(*[, axis, inplace, …])用于**使用后向填充(即“下一个有效观测值”)…...

dvwa11——XSS(Reflected)
LOW 分析源码:无过滤 和上一关一样,这一关在输入框内输入,成功回显 <script>alert(relee);</script> MEDIUM 分析源码,是把<script>替换成了空格,但没有禁用大写 改大写即可,注意函数…...
[KCTF]CORE CrackMe v2.0
这个Reverse比较古老,已经有20多年了,但难度确实不小。 先查壳 upx压缩壳,0.72,废弃版本,工具无法解压。 反正不用IDA进行调试,直接x32dbg中,dump内存,保存后拖入IDA。 这里说一下…...

Go 语言中的内置运算符
1. 算术运算符 注意: (自增)和--(自减)在 Go 语言中是单独的语句,并不是运算符。 package mainimport "fmt"func main() {fmt.Println("103", 103) // 13fmt.Println("10-3…...

android计算器代码
本次作业要求实现一个计算器应用的基础框架。以下是布局文件的核心代码: <LinearLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"andr…...

如何处理React中表单的双向数据绑定?
在前端开发中,双向数据绑定(Two-way Data Binding)是指视图(View)与数据模型(Model)之间保持同步:当模型发生变化时,视图会自动更新;当视图(用户输…...
