做自媒体真的能赚到钱吗?真的能赚到几十万吗?
自媒体在当今社会已经成为一个热门话题,越来越多的人开始尝试做自媒体,希望能够通过自媒体赚到钱。但是,做自媒体真的能赚到钱吗?能赚到几十万吗?下面我们来一一解答。

首先,做自媒体确实可以赚到钱。随着互联网的发展,自媒体已经成为一种新的职业形式。很多人凭借自己的知识、技能、经验等,通过自媒体平台发布内容,吸引粉丝,最终实现盈利。
比如,一些知名自媒体人通过发布文章、视频、直播等方式赚到了不少钱。
其次,赚到钱的多少与自媒体人的能力有关。做自媒体要有一定的能力和素质才能赚到钱。
首先,自媒体人需要有一定的写作能力或者拍摄能力,能够制作出高质量的内容。
其次,自媒体人需要有一定的市场营销能力,能够吸引粉丝,扩大影响力。
最后,自媒体人需要有一定的商业头脑,能够通过自己的影响力赚到钱。
再次,赚到几十万需要很长时间的积累和努力。自媒体并不是一夜之间就能赚到钱的事情,需要长期的积累和努力。
自媒体人需要不断地提高自己的能力和影响力,吸引更多的粉丝,扩大自己的影响力。只有在积累了足够的影响力和粉丝基础之后,才能有机会赚到几十万的收入。
最后,自媒体并不是所有人都适合的职业选择。自媒体需要有一定的创新和创造力,需要不断地更新自己的内容和思路,才能吸引更多的粉丝。
同时,自媒体也需要有一定的专业知识和技能,才能制作出高质量的内容。如果没有这些条件,做自媒体很难赚到钱。
综上所述,做自媒体确实可以赚到钱,但是需要有一定的能力和素质,并且需要长期的积累和努力。赚到几十万需要更多的努力和时间。因此,如果你想要做自媒体,需要认真考虑自己的条件和能力,做好长期的规划和准备。
相关文章:

做自媒体真的能赚到钱吗?真的能赚到几十万吗?
自媒体在当今社会已经成为一个热门话题,越来越多的人开始尝试做自媒体,希望能够通过自媒体赚到钱。但是,做自媒体真的能赚到钱吗?能赚到几十万吗?下面我们来一一解答。 首先,做自媒体确实可以赚到钱。随着互…...
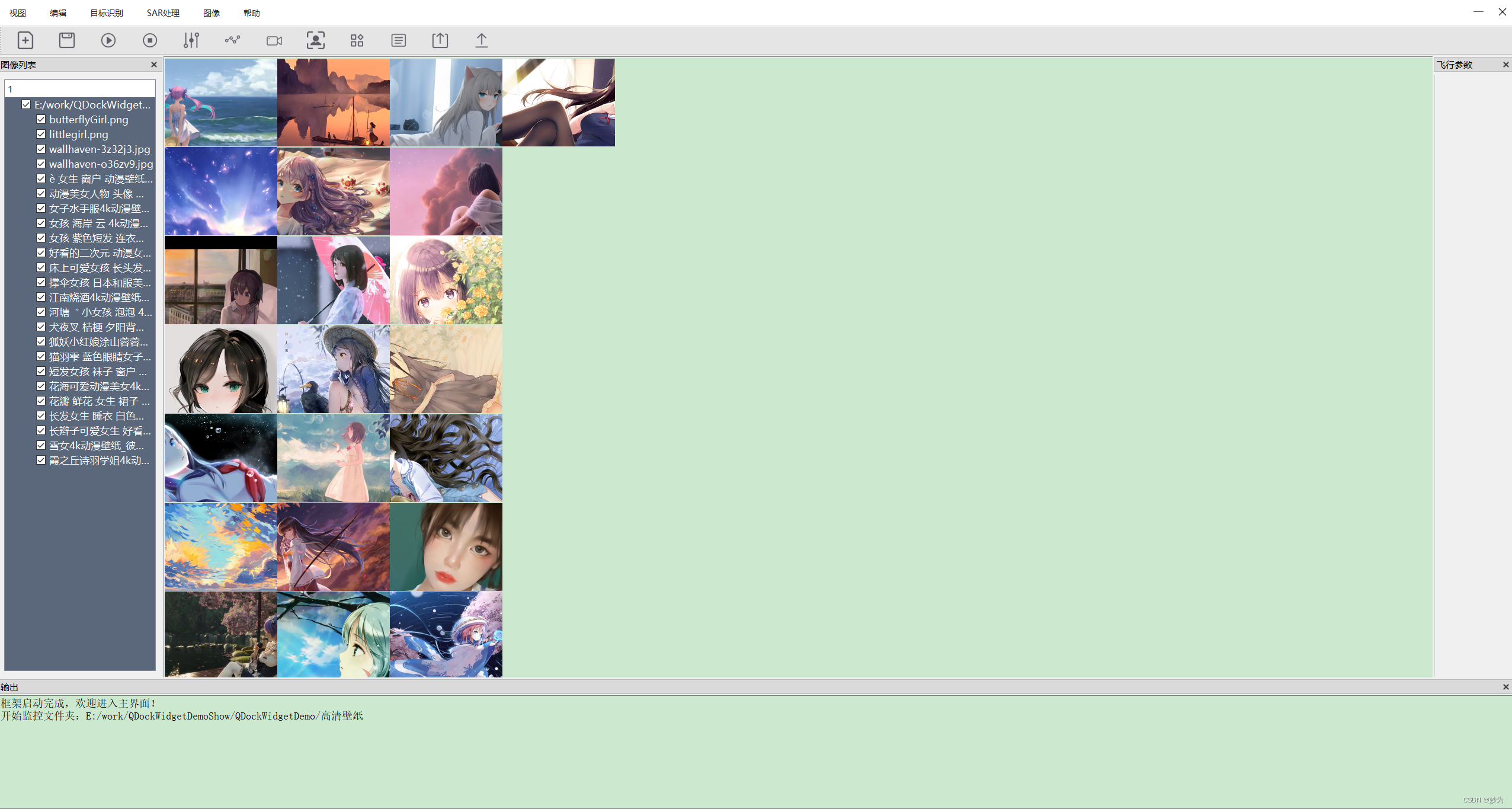
QT使用QListWidget显示多张图片
Qt系列文章目录 文章目录Qt系列文章目录前言一、QListWidget 和 QListView 的差异二、显示效果1.操作工作区界面1.主界面头文件2. 主界面实现界面2.左边图片目录展示界面1.图片目录头文件2.图片目录实现文件2.属性窗口区1.属性窗口头文件2.属性窗口实现文件3 源码下载前言 QLi…...

python 打印进度条
import time recv_size0 total_size1024while recv_size < total_size:time.sleep(0.1)recv_size1024#打印进度条percentrecv_size / total_sizeres int(50 * percent) * #print(\r[%-50s] %d%% % (res,int(100 * percent)),end) # end 打印以‘’结尾,打印% 需…...

【微小说】大学日记
感谢B站up主“看见晴晴了吗”的视频提供的灵感,链接:https://www.bilibili.com/video/BV1tA411m7Kc 整篇故事完全虚构,如有雷同纯属巧合。 2019年8月25日 星期天 晴 今天是我进入大学的第一天。早晨,我画了美美的妆,穿…...

ArrayList扩容机制解析
1.ArrayList的成员变量 首先我们先了解一下ArrayList的成员变量。 // 默认初始化大小 private static final int DEFAULT_CAPACITY 10;// 空数组(用于空实例) // 比如List<String> ls new ArrayList<>(0); private static final Object[…...

jsp-----web应用与开发
jsp基本语法 jsp页面的基本结构 定义变量 <%! %> 表达式:变量、常量、表达式 <% %>代码块、程序段【jsp程序代码即jsp脚本】 <% %>注释 隐藏注释 不会显示在客户的浏览器上,即jsp页面运行后页面上看不到注释内容。同时也不会出…...

洛谷 P1201 [USACO1.1]贪婪的送礼者Greedy Gift Givers
题目链接:P1201 [USACO1.1]贪婪的送礼者Greedy Gift Givers - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 题目描述 对于一群 n 个要互送礼物的朋友,GY 要确定每个人送出的钱比收到的多多少。在这一个问题中,每个人都准备了一些钱来送礼物…...

php设计模式-组合模式的运用
介绍 PHP的组合模式是一种设计模式,用于将对象组合成树形结构以表示“部分-整体”的层次结构。该模式允许客户端统一处理单个对象和组合对象,使得客户端在处理对象时不需要知道对象是否为单个对象还是组合对象。 在组合模式中,有两种类型的…...

一文教会你如何简单使用Fegin进行远程服务调用
文章目录1、fegin的基本介绍2、fegin的基本使用步骤3、项目中的实际运用4、测试前言在分布式微服务中,少不了会进行不同服务之间的相互调用,比如A服务要调用B服务中的接口,如何简单方便的实现呢?fegin可以来帮助。 1、fegin的基本…...

OpenAI——CLIPs(代码使用示例)
OpenAI——CLIPs(打通NLP与CV) Open AI在2021年1月份发布Contrastive Language-Image Pre-training(CLIP),基于对比文本-图像对对比学习的多模态模型,通过图像和它对应的文本描述对比学习,模型能够学习到文本-图像对的匹配关系。它开源、多模态、zero-s…...

什么样的人更适合创业?那类人创业更容易成功?
创业是一项充满风险和机遇的事业,成功的创业者需要具备一定的素质和能力。那么,什么样的人更适合创业?哪类人创业更容易成功呢?本文将为您介绍几个适合创业的人群和成功创业者的共同特点。 具有创新精神的人 创业需要不断创新&am…...

JavaApi操作ElasticSearch(强烈推荐)
ElasticSearch 高级 1 javaApi操作es环境搭建 在elasticsearch官网中提供了各种语言的客户端:https://www.elastic.co/guide/en/elasticsearch/client/index.html 而Java的客户端就有两个: 不过Java API这个客户端(Transport Client&#…...

NFT的前景,元宇宙的发展
互联网的普及和数字技术的广泛应用,成为消费升级的新动力,在不断创造出更好的数字化生活的同时,也改变了人们的消费习惯、消费内容、消费模式,甚至是消费理念,数字经济时代的文化消费呈现出新的特征。 2020年有关机构工…...

C#基础教程20 预处理器指令
文章目录 C#预处理指令教程简介预处理指令格式指令名 参数预处理指令类型条件编译指令if#if 条件表达式宏定义指令总结C#预处理指令教程 简介 预处理指令是在编译代码之前进行的一种处理,可以让程序员在编译前根据需要对代码进行一些修改、调整或者控制。C#语言中的预处理指令…...

【FPGA】Verilog:时序电路设计 | 二进制计数器 | 计数器 | 分频器 | 时序约束
前言:本章内容主要是演示Vivado下利用Verilog语言进行电路设计、仿真、综合和下载 示例:计数器与分频器 功能特性: 采用 Xilinx Artix-7 XC7A35T芯片 配置方式:USB-JTAG/SPI Flash 高达100MHz 的内部时钟速度 存储器&#…...

国外SEO策略指南:确保你的网站排名第一!
如果你想在谷歌等搜索引擎中获得更高的排名并吸引更多的流量和潜在客户,那么你需要了解一些国外SEO策略。 下面是一些可以帮助你提高谷歌排名的关键策略。 网站结构和内容优化 谷歌的搜索算法会考虑网站的结构和内容。 因此,你需要优化网站结构&…...

Tik Tok新手秘籍,做好五点可轻松起号
新手做TikTok需要有一个具体的规划布局,如果没有深思熟虑就上手开始的话,很有可能会导致功亏一篑,甚至是浪费时间。因此,想要做好 TikTok,就必须从最基本的运营细节开始,一步一步来,下面为大家分…...
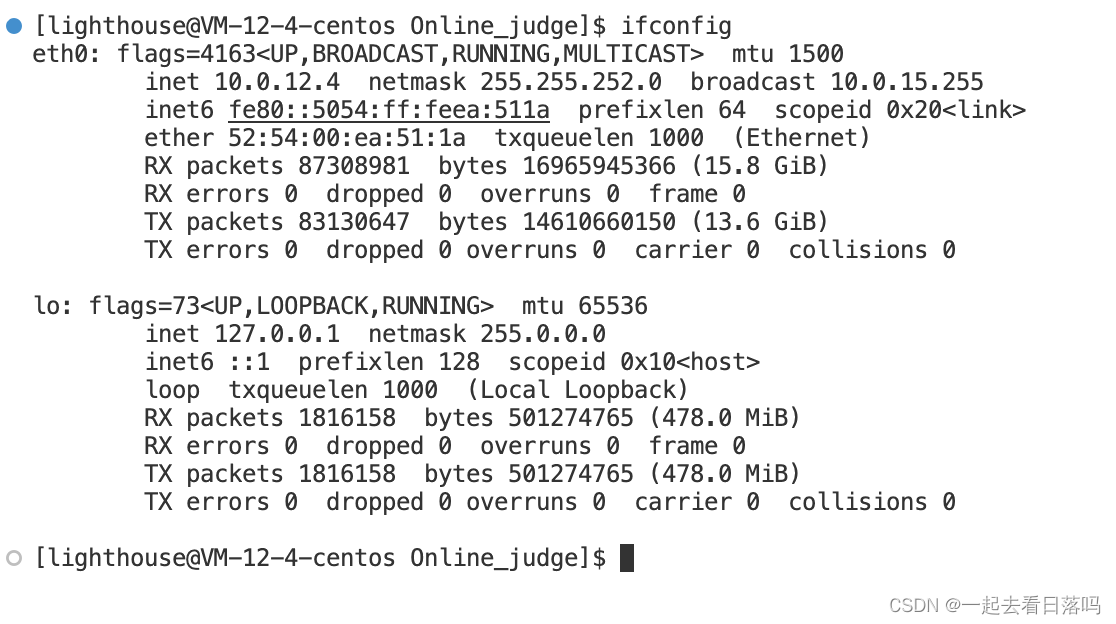
【Linux】网络入门
🎇Linux: 博客主页:一起去看日落吗分享博主的在Linux中学习到的知识和遇到的问题博主的能力有限,出现错误希望大家不吝赐教分享给大家一句我很喜欢的话: 看似不起波澜的日复一日,一定会在某一天让你看见坚持…...
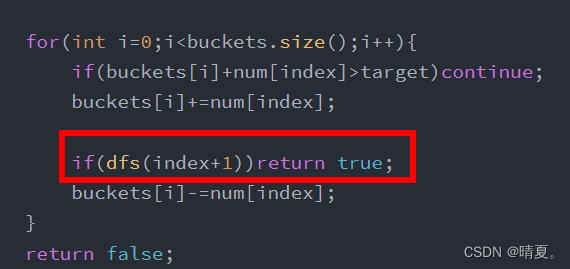
回溯法——力扣题型全解【更新中】
(本文源自网上教程的笔记) 回溯基础理论 回溯搜索法,它是一种搜索的方式。 回溯是递归的副产品,只要有递归就会有回溯。 所以以下讲解中,回溯函数也就是递归函数,指的都是一个函数。 回溯法的效率 虽然…...

【华为机试真题详解 Python实现】分奖金【2023 Q1 | 100分】
文章目录 前言题目描述输入描述输出描述示例 1题目解析参考代码前言 《华为机试真题详解》专栏含牛客网华为专栏、华为面经试题、华为OD机试真题。 如果您在准备华为的面试,期间有想了解的可以私信我,我会尽可能帮您解答,也可以给您一些建议! 本文解法非最优解(即非性能…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
