统计信号处理-匹配滤波器实现与验证（matlab仿真）

什么是匹配滤波器

匹配滤波器是一种信号处理技术，它用于从噪声中提取信号，特别是在信号与噪声比率较低的情况下。匹配滤波器之所以存在，是因为它在信号检测和估计方面具有几个关键的优势：

1. 最大化信噪比：匹配滤波器设计成最大化信号与噪声比率（SNR），这有助于信号的检测和估计。

2. 最优检测：在统计意义上，匹配滤波器提供了最优的信号检测性能，即在给定的信噪比下，它能够以最高的概率检测到信号。

3. 时间延迟：匹配滤波器能够提供最小的时间延迟，这意味着信号可以在尽可能短的时间内被检测到。

4. 波形匹配：匹配滤波器与预期信号的波形匹配，这使得它能够针对特定的信号进行优化。

5. 应用广泛：匹配滤波器在许多领域都有应用，包括雷达、通信、声纳、医学成像等。

6. 理论基础：匹配滤波器基于Wiener滤波器理论，它是一种理想化的滤波器，可以在给定的噪声条件下提供最优的信号估计。

7. 信号恢复：在信号被噪声污染的情况下，匹配滤波器可以帮助恢复信号的原始形状。

8. 简单高效：虽然匹配滤波器在理论上是理想的，但在实际应用中，它可以通过简化的模型来实现，这些模型既简单又高效。

匹配滤波器的工作原理是通过将接收到的信号与信号的复共轭（时间反转）进行卷积，然后对结果进行积分，从而实现信号的增强和噪声的抑制。这种方法在信号检测和估计中非常有效，尤其是在信号已知且噪声是加性白噪声的情况下。

匹配滤波怎么实现

匹配滤波器的实现通常包括以下几个步骤：

1. 信号模型：首先，需要有一个信号模型，即你期望接收到的信号的确切形式。这个模型通常是基于信号的预期特性，例如，信号的波形、持续时间等。

2. 信号的傅里叶变换：将信号模型进行傅里叶变换，得到其频域表示。这个频域表示将用于匹配滤波器的设计。

3. 设计匹配滤波器：匹配滤波器的频率响应是信号模型的复共轭（如果考虑实数信号，则为共轭）。这意味着，如果信号模型是s(t)，那么匹配滤波器的频率响应将是S∗(f)，其中S(f)是信号模型的傅里叶变换，S∗(f)是其复共轭。

4. 接收信号的傅里叶变换：当接收到实际的信号时，需要对它进行傅里叶变换，以得到其频域表示。

5. 频域乘法：将接收信号的傅里叶变换与匹配滤波器的频率响应相乘。这一步在频域中完成，是匹配滤波器的核心操作。

6. 逆傅里叶变换：将乘法的结果进行逆傅里叶变换，以得到时域中的输出信号。这个输出信号是经过匹配滤波器处理的结果，它应该具有增强的信号成分和抑制的噪声成分。

7. 阈值检测：在时域输出信号上设置一个阈值，用于检测信号的存在。如果输出信号在某个时间点的幅度超过阈值，则可以认为信号被成功检测。

8. 信号估计和参数提取：在信号被检测到之后，可以根据输出信号估计信号的参数，例如到达时间、幅度、频率等。

匹配滤波器的实现可以利用快速傅里叶变换（FFT）算法来高效地进行傅里叶变换和逆傅里叶变换，这是在实际应用中常用的技术。FFT算法可以显著减少计算量，使得匹配滤波器在实时系统中更加实用。

在实际应用中，还可能需要考虑信号的不确定性、噪声的特性、多普勒效应等因素，这些都可能影响匹配滤波器的设计和性能。此外，匹配滤波器通常假设信号是已知的，如果信号存在变化或者未知的部分，可能需要采用自适应滤波器或其他更复杂的信号处理技术。

例题和代码解读

解答(1).

由匹配滤波器的知识可得，接收信号可表示为   

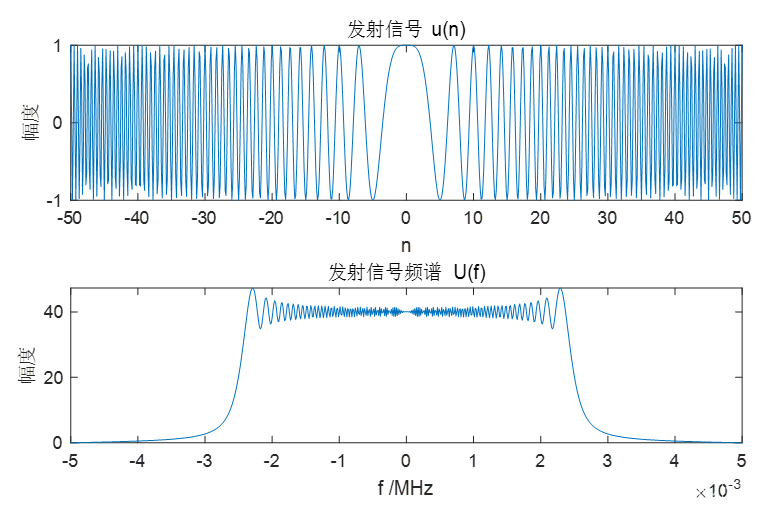
图 1 发射信号仿真图

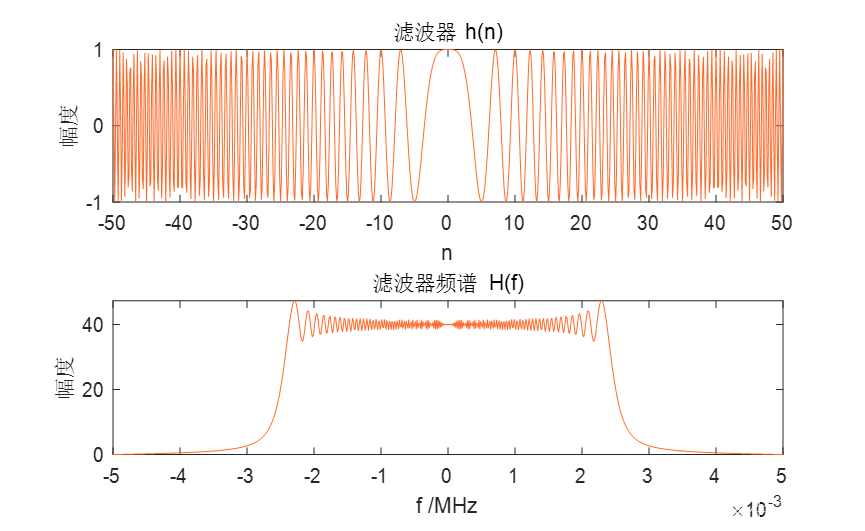
图 2匹配滤波仿真图

则滤波前后的时域实部如下图所示

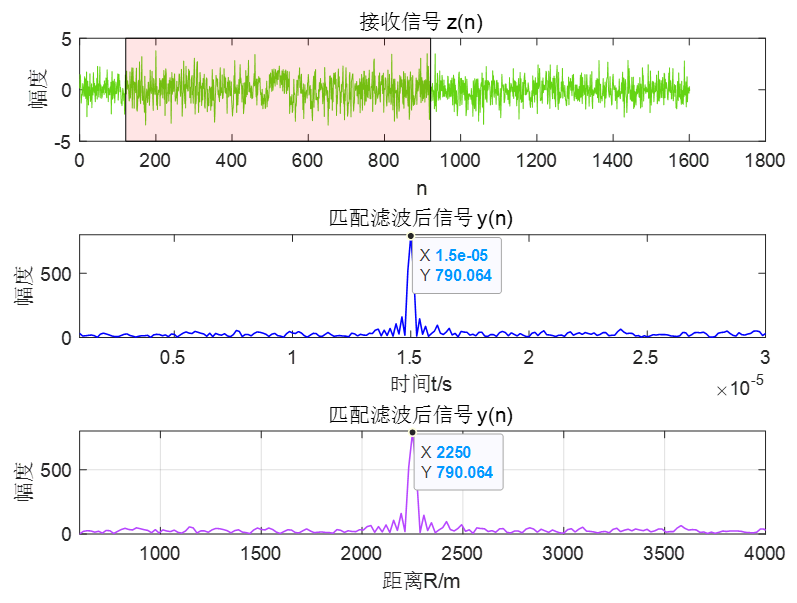
图3 滤波前后对比图

分析：匹配滤波前由于添加了噪声，观测数据长度取信号长度的两倍，图3中红色区域标注了有信号的接收回波段。可以看到在匹配滤波前很难发现信号存在，而匹配滤波后可以明显发现信号的存在。经过匹配滤波之后，可以看出回波被压缩在1.5e-5s处，也即 R=2250m处，与理论推导相符合。

解答(2).

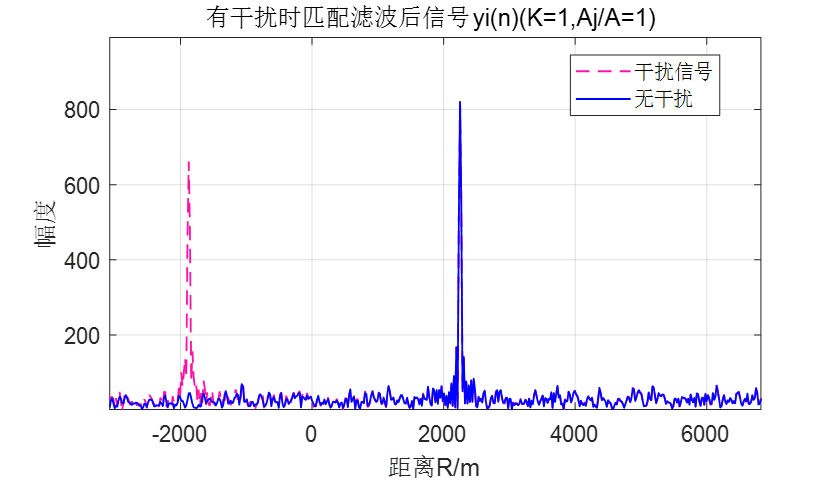
K=1

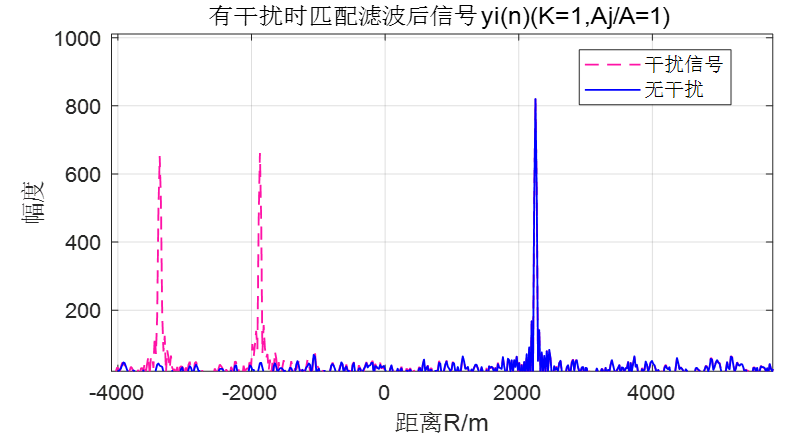
K=2

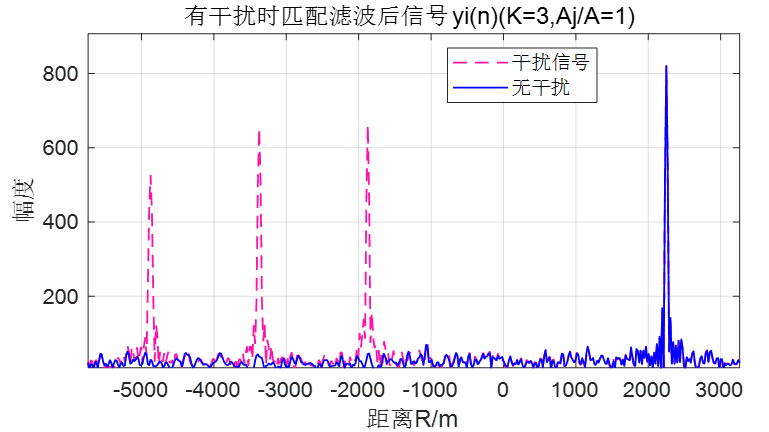
K=3

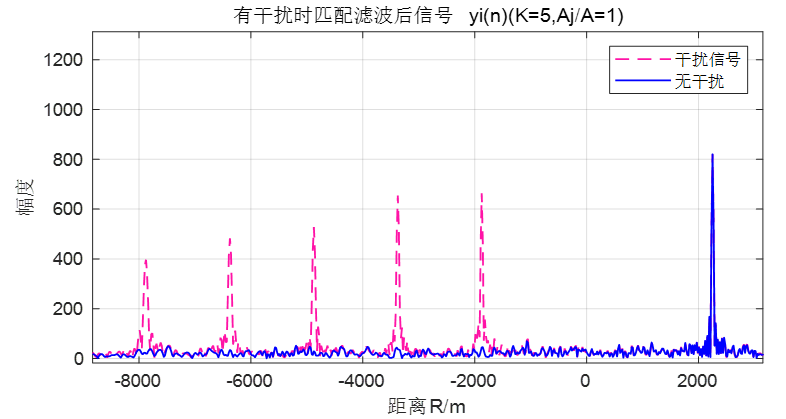
K=5

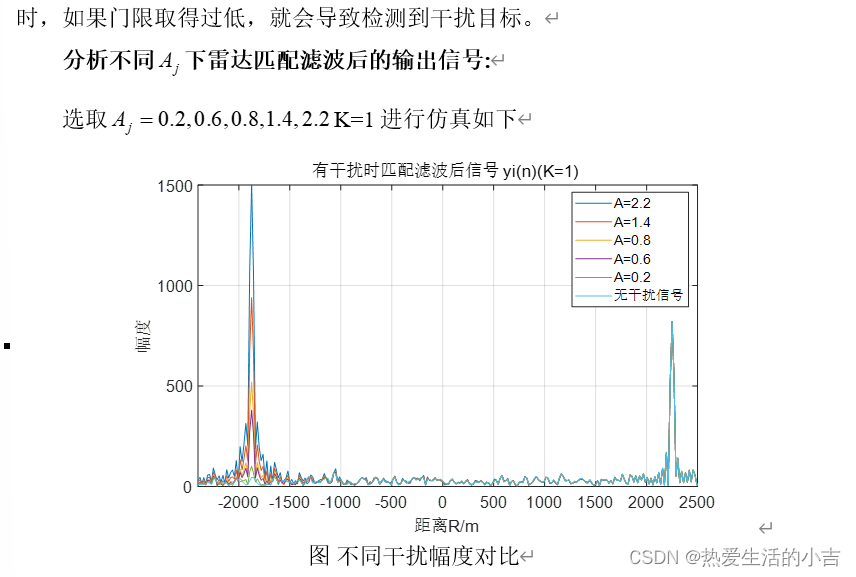
图 不同干扰幅度对比

clearvars;close all; clc;
%% 输入参数
T=1e-4; %脉冲宽度
Ts=1.25e-7; %采样时间间隔
B=4e6; %带宽
c=3e8; %光速
miu=B/T; %调制斜率
A=1; %目标回波幅度
R=2250; %目标距离
t0=2*R/c;
n0=2*R/c/Ts;%目标数字延时
sigma2=1; %噪声方差
noisedB=10*log10(sigma2);
SNRin=A^2/sigma2;%%
Nhalf=round(T/2/Ts);
Nsgrid=(-Nhalf:Nhalf);
Ns=length(Nsgrid); %信号序列的点数
%产生信号
uarr=exp(1i*pi*miu*((Nsgrid)*Ts).^2);
figure()
subplot(2,1,1)
plot(Nsgrid*Ts*1e6,real(uarr));
title('发射信号 u(n)');
xlabel('n');ylabel('幅度');
freq =linspace(-1/2/T,1/2/T,Ns);
%频城采样
Sf = fftshift(fft(uarr));
subplot(2,1,2)
plot(freq*1e-6,abs(Sf))
hold on
title('发射信号频谱 U(f)');
xlabel('f /MHz');
ylabel('幅度');
hold off
%% 产生匹配滤波器
harr=fliplr(conj(uarr)); %匹配滤波器
% 1、根据信号产生匹配滤波器，fliplr 作用是将序列反转即将
% [a1 a2 …… an]变为[an …… a2 a1],这一步等效于书上的关于原点翻转再向右平移 N-1
% 2、注意对于复信号需要取共轭，即 conj()
% 3、对于这种匹配滤波器的产生方式最后输出最大值点在 y[N-1]
figure
subplot(2,1,1)
plot(Nsgrid*Ts*1e6,real(harr))
hold on
xlabel('n');ylabel('幅度');
title('滤波器 h(n)');
freq =linspace(-1/2/T,1/2/T,Ns);
%频城采样
Sf = fftshift(fft(harr));
subplot(2,1,2)
plot(freq*1e-6,abs(Sf))
hold on
title('滤波器频谱 H(f)');
xlabel('f /MHz');
ylabel('幅度');
hold off
%% 产生回波信号
Nz=2*Ns; %观测序列的点数
Nhalf=0;
Nzgrid=(0:Nz-1);
warr=wgn(1,Nz,noisedB); %产生噪声
zarr=zeros(1,Nz);
zarr=zarr+warr; %模拟噪声
% zarr(n0:n0+Ns-1)=zarr(n0:n0+Ns-1)+A*uarr; %模拟回波信号的进入
zarr(n0+1:n0+Ns)=zarr(n0+1:n0+Ns)+A*uarr; %模拟回波信号的进入
% 保证前面有 n0 个 Ts 间隔,及对应于时间间隔为 n0*Ts=2*R/c
t=linspace(-T/2,T/2,Nz);
rtl=A*(abs(t-t0)<T/2).*exp(1j*pi*miu*(t-t0).^2);
figure()
subplot(3,1,1)
plot(Nzgrid,real(zarr));
ax=gca;YLim=ax.YLim;
patch([n0+1-Nhalf n0+1-Nhalf n0+Ns-Nhalf n0+Ns-Nhalf],[YLim(1) YLim(2) YLim(2) YLim(1)],[1,0,0],'facealpha',0.1,'HandleVisibility','off','linewidth',0.1);
title('接收信号 z(n)');
xlabel('n');ylabel('幅度');
hold off
%% 匹配滤波
yarr=filter(harr,1,zarr);
%yarr=conv(zarr,harr);
t1=linspace(-T,T,Ns+Nz-1);
subplot(3,1,2)
plot((Nzgrid-800)*Ts,abs(yarr));
title('匹配滤波后信号 y(n)');
xlim([0.1e-5,0.3e-4])
ylim([0,800])
xlabel('时间t/s');ylabel('幅度');
subplot(3,1,3)
plot((Nzgrid-800)*Ts*c/2,abs(yarr));
title('匹配滤波后信号 y(n)');
xlim([600,4000])
ylim([0,800])
xlabel('距离R/m');ylabel('幅度');
grid on
%% 加入干扰情况%产生干扰信号
K=1; %干扰个数
Aj=0.2;
Ajarr=Aj*ones(1,K)'; %干扰幅度矢量
%这里假设每个干扰幅度一致，可以修改
fj0=0.5e6;
detfj=0.4e6;
fj=(0:K-1)'*detfj+fj0; %干扰频率矢量
ujarr=repmat(Ajarr,1,Ns).*exp(1i*2*pi*fj*Nsgrid*Ts+repmat(1i*pi*miu*(Nsgrid*Ts).^2,K,1));
%干扰信号矩阵(K*Ns) 其中第 j 行表示第 j 个干扰信号
uiarr=sum(ujarr,1); %总的干扰信号
%sum(x,1)表示按列求和
% figure()
% hold on
% plot(Nsgrid,real(uiarr));
% title('干扰信号 ui(n)');
% xlabel('n');ylabel('幅度');
% hold off
ziarr=zarr;
ziarr(1:Ns)=ziarr(1:Ns)+uiarr; %增加干扰后的接收信号
% figure()
% hold on
% plot(Nzgrid,real(ziarr));
% ax=gca;YLim=ax.YLim;
% patch([n0+1-Nhalf n0+1-Nhalf n0+Ns-Nhalf n0+Ns-Nhalf],[YLim(1) YLim(2) YLim(2) YLim(1)],[1,0,0],'facealpha',0.1,'HandleVisibility','off','linewidth',0.1);
% patch([-Nhalf -Nhalf Ns-Nhalf Ns-Nhalf],[YLim(1) YLim(2) YLim(2) YLim(1)],[0,0,1],'facealpha',0.1,'HandleVisibility','off','linewidth',0.1);
% title('干扰后接收信号 zi(n)');
% xlabel('n');ylabel('幅度');
% hold off
yiarr=filter(harr,1,ziarr);plot((Nzgrid-800)*Ts*c/2,abs(yiarr));
title(['有干扰时匹配滤波后信号 yi(n)','(K=',num2str(K),',Aj/A=',num2str(Aj),')']);
xlabel('距离R/m');ylabel('幅度');
%%
hold on
xlim([-2400,2500])
ylim([0,1500])
grid on