排序数组 ---- 分治-归并
题目链接
题目:

分析:
- 用这道题来回顾一下归并排序的思想
- 找到中间结点, 将数组分成两半, 运用递归的思想, 继续对一半进行分半, 分到最后剩一个元素, 再将左右数组合并, 合并两个有序数组, 是先分解, 再合并的过程
- 在合并两个有序数组时, 需要一个额外的数组来记录, 为了避免每次递归都要创建一个新数组浪费空间, 可以将数组定义在全局变量
代码:
class Solution {int[] tmp;public int[] sortArray(int[] nums) {tmp = new int[nums.length];mergeSort(nums, 0, nums.length - 1);return nums;}public void mergeSort(int[] nums, int left, int right) {if (left >= right)return;
//找中间点int mid = left + ((right - left) >> 1);
//划分左边mergeSort(nums, left, mid);
//划分右边mergeSort(nums, mid + 1, right);
//对有序数组进行合并int cur1 = left;int cur2 = mid + 1;int i = 0;while (cur1 <= mid && cur2 <= right) {tmp[i++] = nums[cur1] <= nums[cur2] ? nums[cur1++] : nums[cur2++];}while (cur1 <= mid)tmp[i++] = nums[cur1++];while (cur2 <= right)tmp[i++] = nums[cur2++];for (int j = left; j <= right; j++) {nums[j] = tmp[j - left];}}
}
相关文章:

排序数组 ---- 分治-归并
题目链接 题目: 分析: 用这道题来回顾一下归并排序的思想找到中间结点, 将数组分成两半, 运用递归的思想, 继续对一半进行分半, 分到最后剩一个元素, 再将左右数组合并, 合并两个有序数组, 是先分解, 再合并的过程在合并两个有序数组时, 需要一个额外的数组来记录, 为了避免每…...
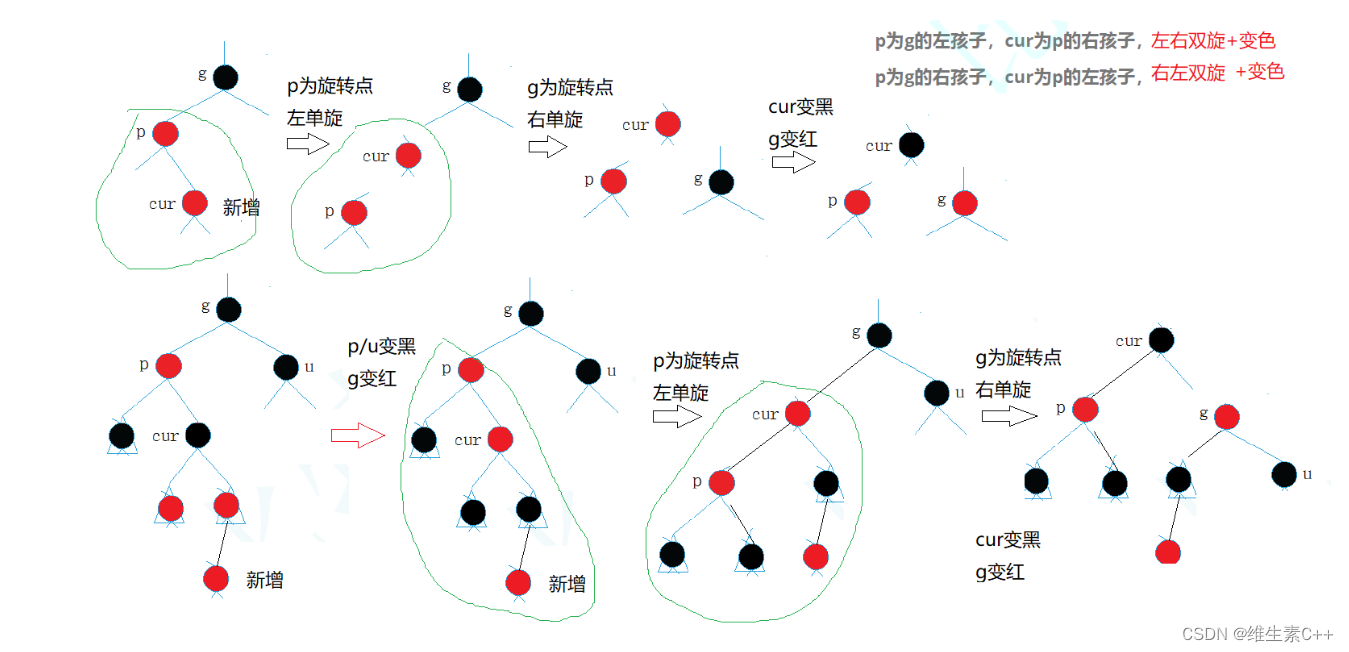
【红黑树变色+旋转】
文章目录 一. 红黑树规则二. 情况一叔叔存在且为红情况二.变色旋旋 一. 红黑树规则 对于红黑树,进行变色旋转处理,终究都是为了维持颜色以下几条规则,只有颜色和规则维持住了,红黑树就维持住了最长路径的长度不超过最短路径的两倍…...

pytorch 使用tensor混合:进行index操作
(Pdb) tmp torch.randn(3,5) (Pdb) indx torch.tensor([1,0]).long() (Pdb) temp(indx) *** NameError: name ‘temp’ is not defined (Pdb) tmp(indx) *** TypeError: ‘Tensor’ object is not callable (Pdb) tmp[indx] tensor([[ 0.1633, 0.9389, 1.2806, -0.2525, 0.28…...
Threejs(WebGL)绘制线段优化:Shader修改gl.LINES模式为gl.LINE_STRIP
目录 背景 思路 Threejs实现 记录每条线的点数 封装原始裁剪索引数据 封装合并几何体的缓冲数据:由裁剪索引组成的 IntArray 守住该有的线段! 修改顶点着色器 修改片元着色器 完整代码 WebGL实现类似功能(简易版,便于测…...

继承-进阶
父子类成员共享 普通成员对象/父子间不共享, 成员独立 函数成员共享(函数不存储在对象中) 子类由两部分构成:父类中继承的成员和子类中新定义成员 继承方式 子类中存在父类private成员但不可直接访问(及时在类中&am…...

探索k8s集群的配置资源(secret和configmap)
目录 ConfigMap ConfigMap(主要是将配置目录或者文件挂载到k8s里面使用) 与Secret类似,区别在于ConfigMap保存的是不需要加密配置的信息。(例如:配置文件) ConfigMap 功能在 Kubernetes1.2 版本中引入&…...

如何设置vue3项目中默认的背景为白色
方法1:通过CSS全局样式 在全局CSS文件中设置: 如果你的项目中有全局的CSS文件(如App.vue或专门的CSS文件),你可以直接设置body或html标签的背景颜色。 在src/assets文件夹中(或者任何你存放CSS文件的地方&a…...

MS1112驱动开发
作者简介: 一个平凡而乐于分享的小比特,中南民族大学通信工程专业研究生在读,研究方向无线联邦学习 擅长领域:驱动开发,嵌入式软件开发,BSP开发 作者主页:一个平凡而乐于分享的小比特的个人主页…...
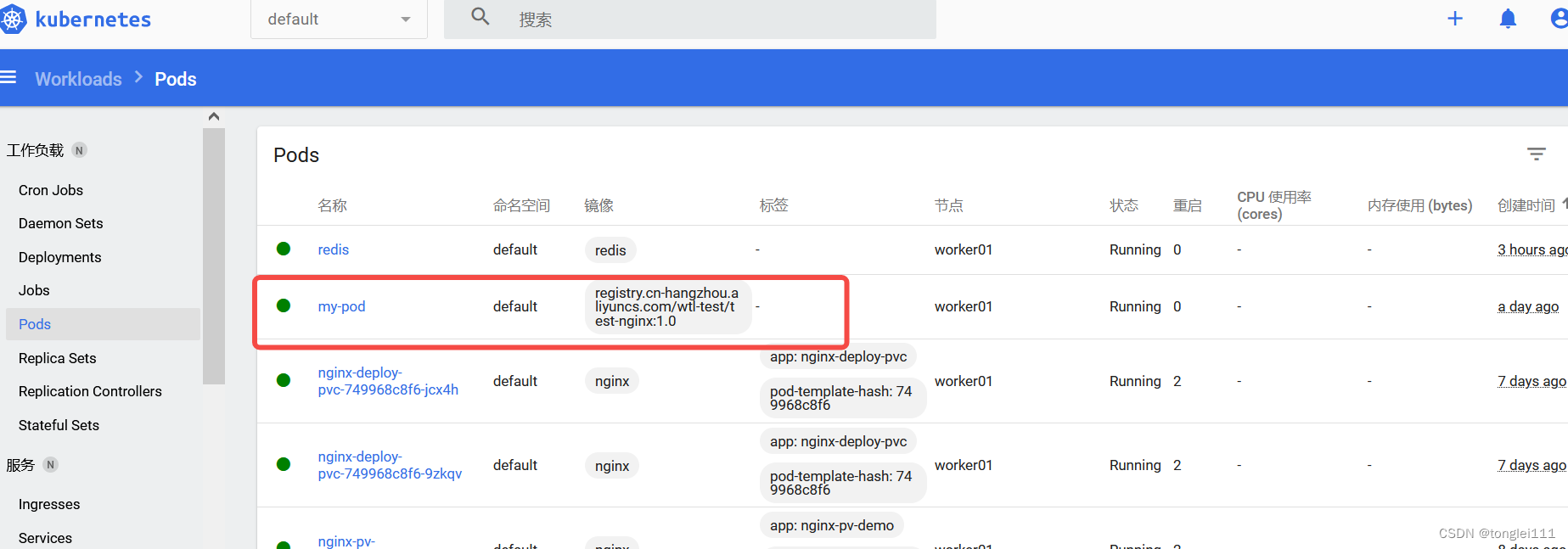
K8s存储对象的使用
背景和概念 容器中的文件在磁盘上是临时存放的,这给在容器中运行较重要的应用带来一些问题: 当容器崩溃或停止时,此时容器状态未保存, 因此在容器生命周期内创建或修改的所有文件都将丢失。另外 在崩溃期间,kubelet 会…...
构建自动化API数据抓取系统
构建一个自动化API数据抓取系统是一个涉及多个技术领域的复杂任务。这样的系统不仅要求高效的数据获取能力,还需要有稳定的数据处理、存储和错误处理机制。 1. 需求分析 在开始构建之前,明确你的需求至关重要。你需要确定要抓取的API、数据的频率、数据的…...
【Qt知识】部分QWidget属性表格
QWidget是Qt库中所有图形用户界面组件的基类,它提供了大量属性以供自定义和配置控件的行为和外观。下面列出了一些主要的QWidget属性及其作用。 属性 作用 accessibleName 控件的辅助技术名称,用于无障碍访问。 accessibleDescription 控件的辅助技…...

【ARM64 常见汇编指令学习 19.1 -- ARM64 跳转指令 b.pl 详细介绍】
文章目录 ARM64 跳转指令 b.pl使用场景语法示例总结 ARM64 跳转指令 b.pl 在 ARMv8 架构中,b.pl 是一条条件分支(Branch)指令,它根据当前的状态寄存器中的条件标志执行跳转。b.pl 的全称是 Branch if Plus,即如果条件…...

WWDC24即将到来,ios18放大招
苹果公司即将在下周开全球开发者大会(WWDC),大会上将展示其人工智能技术整合到设备和软件中的重大进展,包括与OpenAI的历史性合作。随着大会的临近,有关iOS 18及其据称采用AI技术支持的应用程序和功能的各种泄露信息已经浮出水面。 据报道,苹果将利用其自主研发的大…...

C#中的空合并运算符与空合并赋值运算符:简化空值处理
在C#编程中,处理可能为null的值是一项常见的任务,尤其是在涉及数据库查询、Web服务调用或任何可能返回缺失数据的场景中。为了简化这类操作并提高代码的可读性,C# 8 引入了两个非常实用的运算符:空合并运算符 (??) 和 空合并赋值…...

数据结构:哈夫曼树及其哈夫曼编码
目录 1.哈夫曼树是什么? 2.哈夫曼编码是什么? 3.哈夫曼编码的应用 4.包含头文件 5.结点设计 6.接口函数定义 7.接口函数实现 8.哈夫曼编码测试案列 哈夫曼树是什么? 哈夫曼树(Huffman Tree)是一种特殊的二叉树…...
微信如何防止被对方拉黑删除?一招教你解决!文末附软件!
你一定不知道,微信可以防止被对方拉黑删除,秒变无敌。只需一招就能解决!赶快来学!文末有惊喜! 惹到某些重要人物(比如女朋友),被删除拉黑一条龙,那真的是太令人沮丧了&a…...

jar增量打包
jar增量打包 Linux环境下: 1.解压缩 jar -xvf jarname.jar(解压)2.打包 这时可以把要替换的lib包的内容粘帖进去,然后重新打jar包 jar -cvf0M jarname.jar .(重新压缩,-0是主要的)jar命令: …...

智慧医院物联网建设-统一管理物联网终端及应用
近年来,国家卫健委相继出台的政策和评估标准体系中,都涵盖了强化物联网建设的内容。物联网建设已成为智慧医院建设的核心议题之一。 作为医院高质量发展的关键驱动力,物联网的顶层设计与网络架构设计规划,既需要结合现代信息技术的…...

Debian的常用命令
Debian作为一个稳定、安全且高效的Linux发行版,被广泛应用于服务器和桌面操作系统中。对于系统管理员和开发者来说,熟练掌握Debian的常用命令能够大大提升工作的效率和系统的管理水平。本文将详细介绍一些常见且实用的Debian命令,帮助新手更好地管理和操作Debian系统。 系统…...

矩阵1-范数与二重求和的求和可交换
矩阵1-范数与二重求和的求和可交换 1、矩阵1-范数 A [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ] A \begin{bmatrix} a_{11} &a_{12} &\cdots &a_{1n} \\ a_{21} &a_{22} &\cdots &a_{2n} \\ \vdots &\vdots …...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...
