当前位置：首页 > news >正文

【红黑树变色+旋转】

news 2026/2/10 18:56:08

文章目录

一. 红黑树规则
二. 情况一叔叔存在且为红
情况二.变色+旋旋

一. 红黑树规则

对于红黑树，进行变色+旋转处理，终究都是为了维持颜色+以下几条规则，只有颜色和规则维持住了，红黑树就维持住了最长路径的长度不超过最短路径的两倍。

规则：

根是黑的。
没有连续的红节点。
每条路径的黑色数量相等。

二. 情况一叔叔存在且为红

注意点：红黑树插入的节点都是红色的，因为在红黑树中动黑色节点是非常忌讳的，因为要维持每条路径黑色数量相等非常困难，所以插入的节点默认都是红色的。

当插入红色节点后：1.如果父亲为黑或者父亲不存在，结束，不需要任何处理。
2. 如果父亲存在且为红，由于插入节点为红，存在连续红节点，需要处理，可以肯定的是爷爷一定是黑，因为插入节点前就是一棵红黑树了，既然父亲和爷爷颜色确定，主要看叔叔。

1.叔叔存在且为红
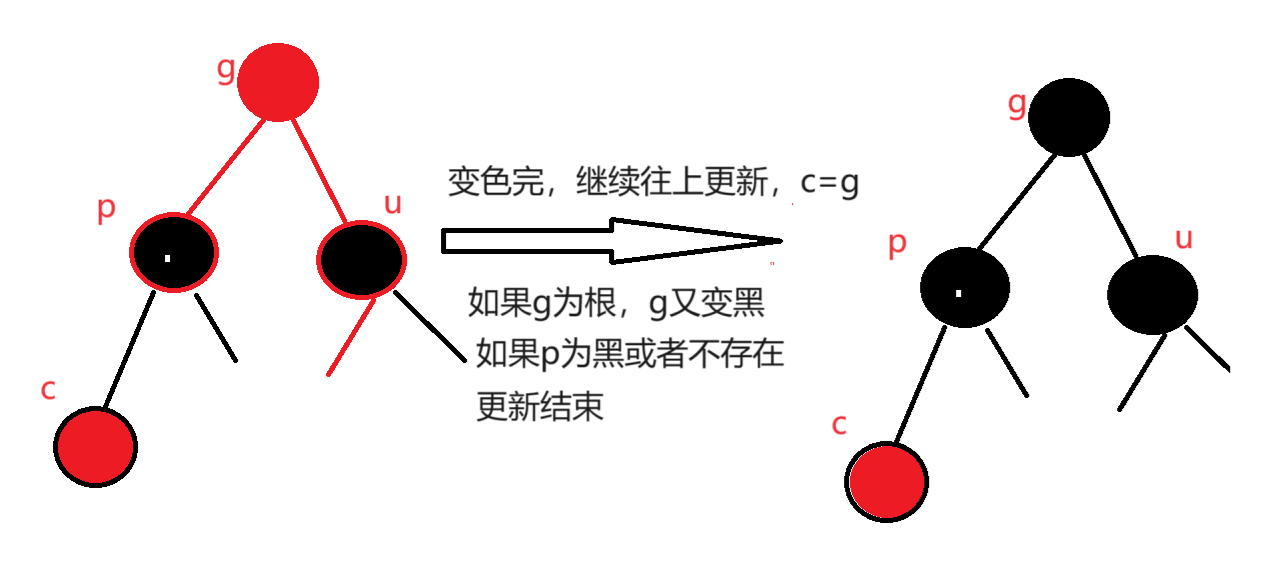
在这里插入图片描述

情况二.变色+旋旋

叔叔存在且为黑或者叔叔不存在都需变色+旋转，关键分析是左单旋，右单旋，还是左右双旋，还是右左双旋只要旋转后，就平衡了，直接结束，不需要向上更新

1. 变色+单旋
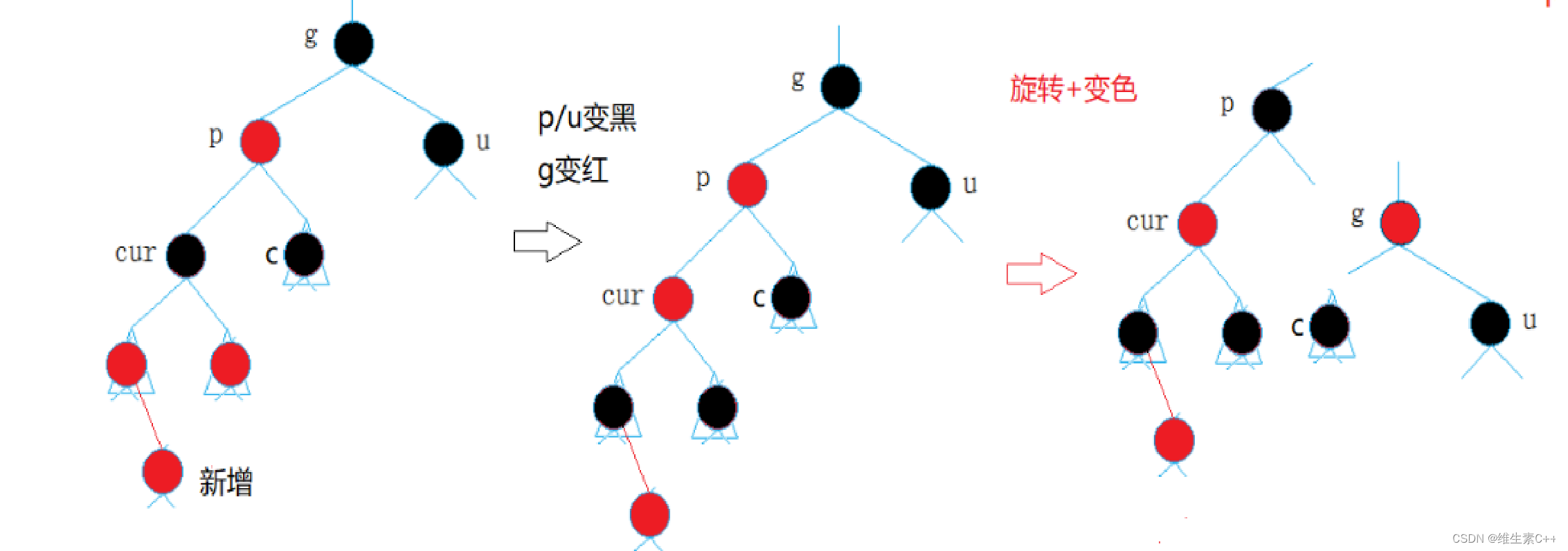
在这里插入图片描述
对于叔叔存在且为黑或不存在这种情况，不可能是因为直接插入红色节点导致连续红这种情况直接发生的，因为这发生了，原本就不是红黑树，一定是由上述图一第一种情况处理更新上来导致的。
解决办法：curp->left, pg->left 左左右单旋g点+
p变黑，g变红。
同理：如果上述情况curp->right, pg->right，右右左单旋g点+p变黑，g变红

2.变色+双旋
在这里插入图片描述
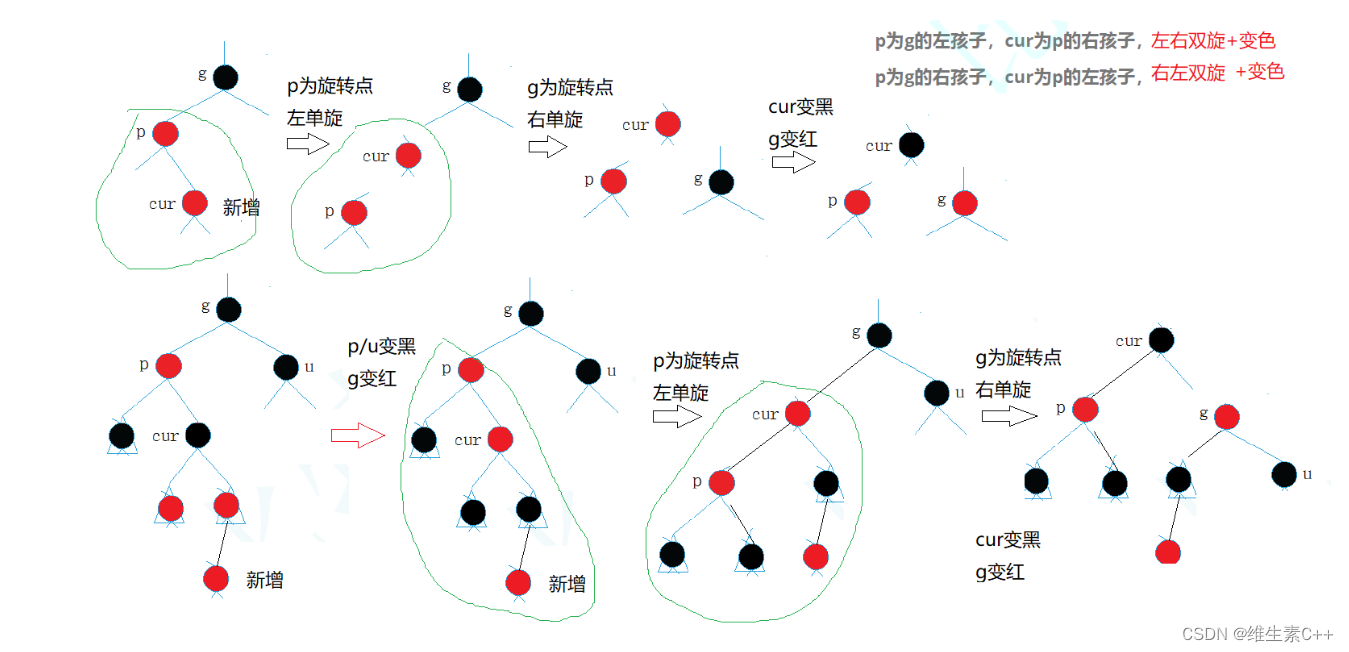
对于这种情况：curp->right, pg->left,左右双旋，
将p左旋，g右旋，+ cur变黑+g变红。

同理：curp->left, pg->right, 右左双旋，将p右旋，g左旋，+cur变黑+g变红

总结单纯变色处理，需要不停向上更新至父亲不存在或者父亲为黑结束，旋转+变色处理完就平衡了直接结束。
一下是代码实现

bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;	//根为黑色return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//父亲存在且为红，连续红节点，处理(如果父亲不存在管你红黑就结束了，如果为黑也结束了）while (parent && parent->_col == RED){Node* grandfather = parent->_parent;  //算出爷爷，根据父亲为爷爷的左右，确定叔叔if (parent == grandfather->_left){Node* uncle = grandfather->_right;//情况一：叔叔存在且为红 变色处理if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//根节点保证为黑下面处理//继续往上处理cur = grandfather;parent = cur->_parent;}//情况二：叔叔不存在/叔叔存在且为黑else{//需要判别单旋还是左旋，确定cur的位置//旋转+变色if (cur == parent->_left){//		g//	 p		u//c//左左右单旋RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//		g//	p		u//	   c//左右双旋+变色RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;	//只要旋转结束就平衡了结束}}else{Node* uncle = grandfather->_left;//情况一：叔叔存在且为红 变色处理if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//根节点保证为黑下面处理//继续往上处理cur = grandfather;parent = cur->_parent;}//情况二：叔叔不存在/叔叔存在且为黑else{if (cur == parent->_right){//		g//	u		p//				cRotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//		g//	u		p//		 c//右左双旋RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}//只要旋转完了，就平衡结束了break;}}}_root->_col = BLACK;	//变色没有处理根，无论怎么处理都保证根是黑的return true;}void RotateL(Node* parent){++rotateSize;Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;Node* ppnode = parent->_parent;parent->_parent = subR;if (_root == parent){_root = subR;subR->_parent = nullptr;}else{if (parent == ppnode->_left){ppnode->_left = subR;}else{ppnode->_right = subR;}subR->_parent = ppnode;}}void RotateR(Node* parent){++rotateSize;Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;Node* ppnode = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (parent == ppnode->_left){ppnode->_left = subL;}else{ppnode->_right = subL;}subL->_parent = ppnode;}}

无论怎么方式处理完都需要保证根是黑的，最后加上