【ARM 常见汇编指令学习 6.2 -- ARMv8 汇编指令 SDIV 详细介绍】
文章目录
- SDIV
- 指令格式
- 使用示例
- 注意事项
- 总结
SDIV
ARMv8 架构中的 SDIV 指令用于执行带符号整数除法操作。这意味着它可以处理负数除法,与 UDIV(执行无符号整数除法)形成对比。SDIV 将两个寄存器中的带符号整数相除,将除法结果存储在目标寄存器中。
指令格式
SDIV 的基本语法如下:
SDIV <Xd>, <Xn>, <Xm>
或者对于 32 位寄存器:
SDIV <Wd>, <Wn>, <Wm>
<Xd>或<Wd>是目标寄存器,用于存储除法的结果。<Xn>或<Wn>是被除数(Dividend)。<Xm>或<Wm>是除数(Divisor)。
在这里,X寄存器是 64 位的,而W寄存器是 32 位的。使用哪一种寄存器取决于操作数的大小需求。
使用示例
以下是一些 SDIV 指令的使用示例:
// 32 位除法示例
SDIV W0, W1, W2 // W0 = W1 / W2,使用32位寄存器
// 64 位除法示例
SDIV X0, X1, X2 // X0 = X1 / X2,使用64位寄存器
注意事项
- 如果除数为 0,ARMv8 架构并未明确规定
SDIV指令的行为。在不同的实现中,结果可能不同,因此在执行SDIV指令前,确保除数不为 0 是很重要的。 SDIV的执行速度可能比加法、减法和乘法指令慢,因为除法是一个更复杂的运算。因此,应当谨慎使用除法,特别是在性能敏感的代码区域。- 在进行带符号除法时,正负数的处理遵循标准的数学规则。例如,正数除以负数得到负数,负数除以负数得到正数等。
SDIV只返回除法操作的商,如果需要余数,则需要使用其他指令和方法来单独计算。
总结
SDIV 指令在 ARMv8 架构中提供了一种执行带符号整数除法的直接方法。虽然它在使用上相对直接简单,但编程时需要注意除数为 0 的情况,并且要意识到除法操作的性能成本。在设计算法和实现软件时,适当的优化可以帮助提高除法操作的整体效率。
相关文章:

【ARM 常见汇编指令学习 6.2 -- ARMv8 汇编指令 SDIV 详细介绍】
文章目录 SDIV指令格式使用示例注意事项总结 SDIV ARMv8 架构中的 SDIV 指令用于执行带符号整数除法操作。这意味着它可以处理负数除法,与 UDIV(执行无符号整数除法)形成对比。SDIV 将两个寄存器中的带符号整数相除,将除法结果存…...

【ArcGIS微课1000例】0113:大地测量要素概述与构建
文章目录 一、大地测量要素描述1. 大地要素的概念2. 大地要素的类型二、创建大地测量要素1. 创建要素类2. 创建大地要素一、大地测量要素描述 1. 大地要素的概念 大地测量要素的测量值考虑了投影空间的固有变形。如果要创建一个空间跨度较大的要素(例如一条横跨大洋的飞行路…...
)
【记录】LangChain+本地模型的文档问答(webUI)
已在notebook测试无误。 包安装 pip install langchain langchain_community transformers InstructorEmbedding sentence_transformers2.2.2 faiss-gpu PyPDF2 streamlit pyngrok gradio fitz frontend 环境变量设置 huggingface连不上无法下载模型,需要设置镜像。…...
Winddow系统下关于Golang使用Cgo的配置
1.配置CGO_ENABLED为1 go env -w CGO_ENABLED1 2.安装gcc环境,否则出现cgo: C compiler "gcc" not found: exec: "gcc": executable file not found in %PATH%错误 安装包:链接:https://pan.baidu.com/s/1sgF9lijqGeP…...

python面向过程与初始面向对象编程
让我们穿越到《龙珠》世界,一起揭开 面向对象编程 的神秘面纱吧。 面向过程编程与面向对象编程 天下第一武道会 选手登记 第 22 届天下第一武道会即将召开,各路武术高手齐聚一堂,其中最受瞩目的,当属卡卡罗特(孙悟…...

vue3 实现自定义指令封装 --- 通俗易懂
1、局部自定义指令 1.1 在<script setup>定义组件内的指令,任何以v开头的驼峰式命名的变量都可以被用作一个自定义指令 <template><div><h3>使用自定义指令</h3><div>########################## start 局部自定义指令</d…...

5.31.15 使用图像到图像转换和 YOLO 技术对先前的乳房 X 光检查结果中的异常进行早期检测和分类
在本研究中,我们研究了基于 You-Only-Look-Once (YOLO) 架构的端到端融合模型的有效性,该模型可同时检测和分类数字乳房 X 光检查中的可疑乳腺病变。包括四类病例:肿块、钙化、结构扭曲和正常,这些病例来自包含 413 个病例的私人数…...
题解web
1.[LitCTF 2023]Follow me and hack me 1)进入题目环境,提示get传参,post传参 2)看看源码,也没啥 3)直接用hackbar,传入对应参数即可得到FLAG 3)但是扫描出来它后端还有东西&#x…...

在keil5中打开keil4工程的方法
文章目录 1. 打开文件 2. 安装旧版本包 3. 在keil4中打开keil5工程 1. 打开文件 在keil5 MDK的环境下,打开keil4的工程文件,会弹出下图所示的窗口: 参考官网的解释这两个方法分别为: 1. 使用MDK 版本 4 Legacy Pack时&#x…...

【代码随想录算法训练营第37期 第二十四天 | LeetCode77. 组合】
代码随想录算法训练营第37期 第二十四天 | LeetCode77. 组合 一、77. 组合 解题代码C: class Solution { private:vector<vector<int>> result;vector<int> path;void backtracking(int n, int k, int startIndex){if(path.size() k){result.p…...

探索Linux中的`tree`命令:目录结构的可视化利器
探索Linux中的tree命令:目录结构的可视化利器 在Linux系统中,管理文件和目录结构是一项日常任务。当我们需要快速查看目录的层次结构时,tree命令无疑是一个强大而直观的工具。本文将详细介绍tree命令的功能、用法以及一些实用的选项。 一、…...

ES 面试手册
Elasticsearch是什么? Elasticsearch是一个基于Lucene的搜索和分析引擎,它提供了一个分布式、多租户能力的全文搜索引擎,具有HTTP Web界面和无模式JSON文档。 Elasticsearch中的倒排索引是什么? 倒排索引是搜索引擎的核心结构&a…...

Mybatis缓存的生命周期、使用的特殊情况
以下场景均在Spring Boot程序中,并非手动创建SqlSession使用。 在回答这个问题之前,我们先来回顾一下,Mybatis的一级二级缓存是啥。 一级二级缓存 是什么 一级缓存(本地缓存):一级缓存是SqlSession级别的…...

day 37 738.单调递增的数字
738. 单调递增的数字 当且仅当每个相邻位数上的数字 x 和 y 满足 x < y 时,我们称这个整数是单调递增的。 给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。 示例 1: 输入: n 10 输出: 9示例 2: 输入: n 1234 输…...

【加密与解密】【01】网络安全体系
网络通信OSI模型 物理层(Physical)链路层(DataLink)网络层(Network)传输层(Transport)会话层(Session)表示层(Presentation)应用层&a…...
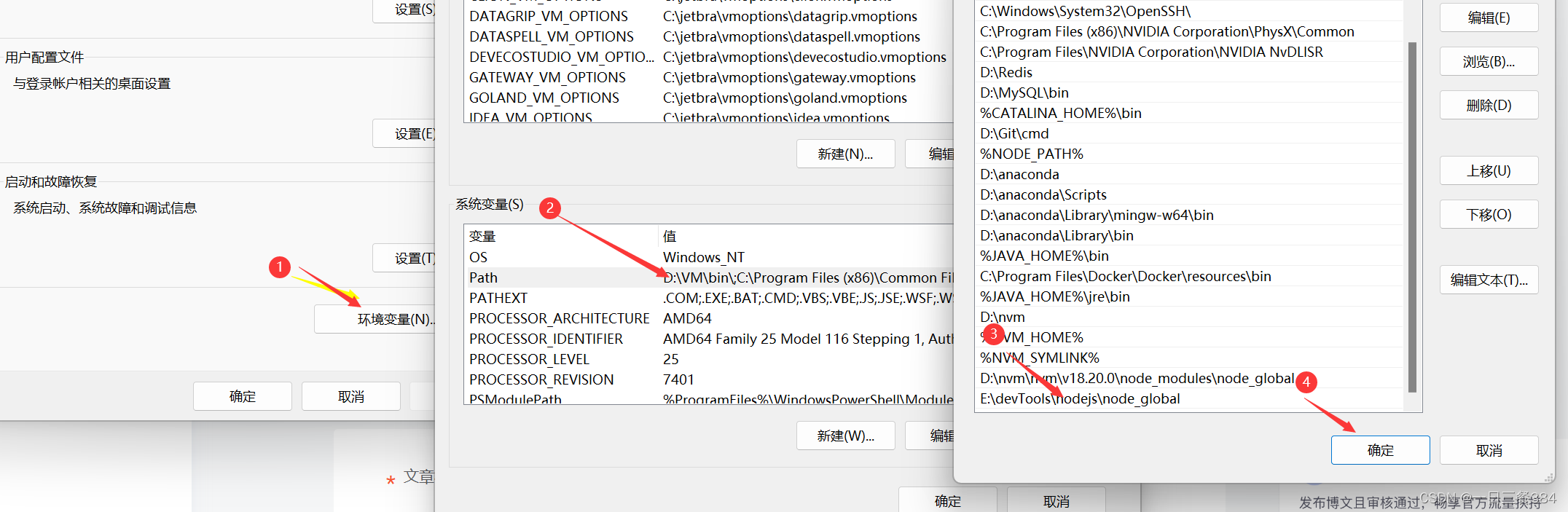
nvm,node不是内部命令,npm版本不支持问题(曾经安装过nodejs)
nvm安装后nvm -v有效,node指令无效 环境变量配置无问题 推荐方案 下载你需要的node版本 Index of /dist/ (nodejs.org) 下载后解压到你的nvm存储版本的位置 cmd进入切换你的使用版本(此时你的nodejs是从网上下载的,npm文件是存在的&…...

从入门到精通:基础IO
引言 在编程的世界里,文件输入输出(IO)是与操作系统交互的重要方式。无论你是开发应用程序、处理数据,还是管理系统资源,掌握文件IO操作都是必不可少的。本篇博客将带你深入了解C语言中的基础IO操作,从入门…...
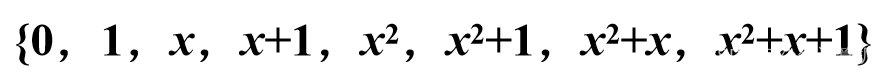
网络空间安全数学基础·多项式环与有限域
5.1 多项式环(掌握) 5.2 多项式剩余类环(理解) 5.3 有限域(熟练) 5.1 多项式环 定义:设F是一个域,称是F上的一元多项式. 首项:如果an≠0,则称 a…...
路由器重启真的好吗?多久重启一次更好?
前言 小白前段时间发现自己家的OpenWRT软路由上网特别慢,有时候通话还有点卡顿。 然而有个朋友用的普通路由器也有类似的问题,而且有时候根本上不去网。 解决的办法很简单:重启路由器。 重启路由器? 但路由器重启是真的好吗&a…...

删除目录
自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 删除目录可以通过使用os模块提供的rmdir()函数实现。通过rmdir()函数删除目录时,只有当要删除的目录为空时才起作用。rmdir()函数的基本语…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序,无论是测试应用程序、搜寻漏洞还是收集情报,它们都能提升工作流程。 FoxyProxy 代理管理工具,此扩展简化了使用代理(如 Burp…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...

聚六亚甲基单胍盐酸盐市场深度解析:现状、挑战与机遇
根据 QYResearch 发布的市场报告显示,全球市场规模预计在 2031 年达到 9848 万美元,2025 - 2031 年期间年复合增长率(CAGR)为 3.7%。在竞争格局上,市场集中度较高,2024 年全球前十强厂商占据约 74.0% 的市场…...
