负氧离子监测站:打造健康生态的守护者
TH-FZ5随着人们对生活质量和健康水平的要求日益提高,空气质量成为了公众关注的焦点。其中,负氧离子作为空气中的一种重要成分,对人体健康有着显著的影响。负氧离子监测站作为监测空气中负氧离子浓度的专业设备,在现代环境监测和生态保护中发挥着至关重要的作用。本文将详细介绍负氧离子监测站的定义、工作原理、应用场景以及未来发展趋势。
二负氧离子监测站的定义与工作原理
-
定义:负氧离子监测站是一种专门用于实时监测空气中负氧离子浓度的设备。它通过先进的传感器技术和数据处理系统,能够准确测量并显示空气中负氧离子的浓度和变化趋势。
-
工作原理:负氧离子监测站的工作原理基于负氧离子的物理和化学特性。传感器通过捕捉空气中负氧离子与带电粒子之间的相互作用,将其转化为电信号输出。数据处理系统对这些电信号进行放大、滤波和数字化处理,最终得到负氧离子的浓度值,并通过显示屏或其他方式呈现给用户。
负氧离子监测站的应用场景
-
生态环境监测:负氧离子监测站可用于森林、公园、湖泊等自然生态环境中,实时监测负氧离子浓度,评估生态环境质量,为生态保护提供科学依据。
-
空气质量监测:在城市道路、工业区、居民区等区域设置负氧离子监测站,可以实时监测空气质量,为居民提供健康出行建议,并为政府制定空气质量政策提供数据支持。
-
旅游景区:旅游景区通常拥有优美的自然风光和丰富的负氧离子资源。在景区内设置负氧离子监测站,不仅可以为游客提供实时的空气质量信息,还可以提升景区的吸引力,促进旅游业的发展。
负氧离子监测站能够实时、连续地监测空气中负氧离子的浓度和变化趋势,为用户提供及时、准确的数据支持精度高:采用先进的传感器技术和数据处理系统,负氧离子监测站具有较高的测量精度和稳定性。

相关文章:

负氧离子监测站:打造健康生态的守护者
TH-FZ5随着人们对生活质量和健康水平的要求日益提高,空气质量成为了公众关注的焦点。其中,负氧离子作为空气中的一种重要成分,对人体健康有着显著的影响。负氧离子监测站作为监测空气中负氧离子浓度的专业设备,在现代环境监测和生…...
在调用接口上map与forEach的区别
在场景:一个表格数据需要上传,每行表格需要上传图片->这就需要在提交时对数据也就是数组进行处理(先将每个元素图片上传拿到图片id 这种情况我刚开始就用的map处理,然后问题来了,提交的接口调用了,但是…...
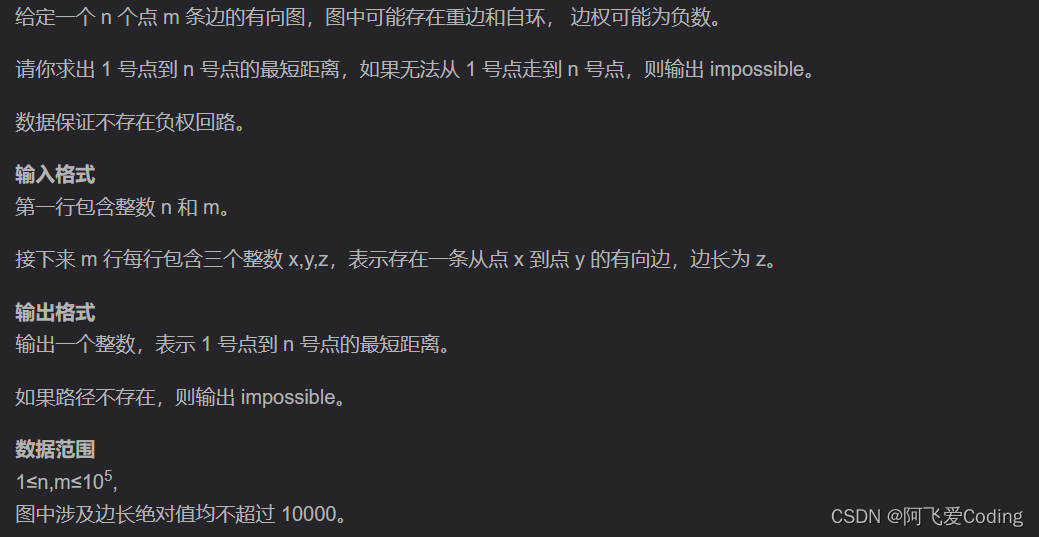
最短路:spfa算法
最短路:spfa算法 题目描述参考代码 题目描述 参考代码 输入示例 3 3 1 2 5 2 3 -3 1 3 4输出示例 2#include <iostream> #include <cstring> #inc…...

算法笔记 图论和优先级队列的笔记
图论 DFS stack O(h) 不具有最短性 BFS queue O(2^h) 最短路 迪杰斯特拉算法 初始化: 将起始节点 A 的距离设为 0。将其他所有节点的距离设为无穷大。创建一个优先队列,并将起始节点 A 加入优先队列。 处理队列: …...
6.每日LeetCode-数组类,找到所有数组中消失的数字
题目 448找到所有数组中消失的数字.go 给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。 示例 1: 输入:nums [4,3,2,7,8,2,…...

【Three.js】知识梳理十:Three.js纹理贴图
1. 纹理贴图 在Three.js中,纹理贴图是一种将二维图像贴到三维物体表面的技术,以增强物体的视觉表现。纹理贴图可以使物体表面更加真实、细腻,为场景增色不少。 在Three.js中,纹理贴图的加载主要通过THREE.TextureLoader类实现。…...

mysql order by后跟case when
在SQL中,ORDER BY子句用于对查询结果进行排序。当在ORDER BY后面使用CASE语句时,它的原理是:根据CASE语句中定义的条件和结果,为查询结果集中的每一行生成一个临时的排序值。然后,根据这些排序值对结果集进行排序。 具…...

数字孪生赋能的智慧园区物联网云平台建设方案(97页PPT)
方案介绍: 本方案通过数字孪生技术赋能智慧园区物联网云平台,实现了园区的智能化管理、优化资源配置、提高运营效率等目标。同时提升园区的安全性、环保性和可持续性。最后,该方案还充分考虑了系统的可扩展性、安全性和可靠性,为…...

TikTok小店运营策略
TikTok,作为一款全球知名的短视频社交平台,其用户基数庞大且日活跃用户持续增长,为商家提供了巨大的商机。欧洲作为TikTok的重要市场之一,其小店功能为商家提供了一个展示和销售产品的新渠道。本文将探讨如何有效地运营TikTok小店…...

Docker面试整理-如何查看和管理Docker容器的日志?
管理和查看 Docker 容器的日志是 Docker 容器管理的重要部分,有助于监控应用的行为和诊断问题。Docker 提供了几种方法来查看和管理容器日志。 查看容器日志 要查看 Docker 容器的日志,你可以使用 docker logs 命令。这个命令会打印容器的 STDOUT 和 STDERR 输出,这是大多数…...

Java从放弃到继续放弃
并发编程 为什么需要多线程? 由于硬件的发展,CPU的核数增多,如果仍然使用单线程对CPU资源会造成浪费。同时,单线程也会出现阻塞的问题。所以,选择向多线程转变。 多线程的使用使得程序能够并行计算,提高计…...
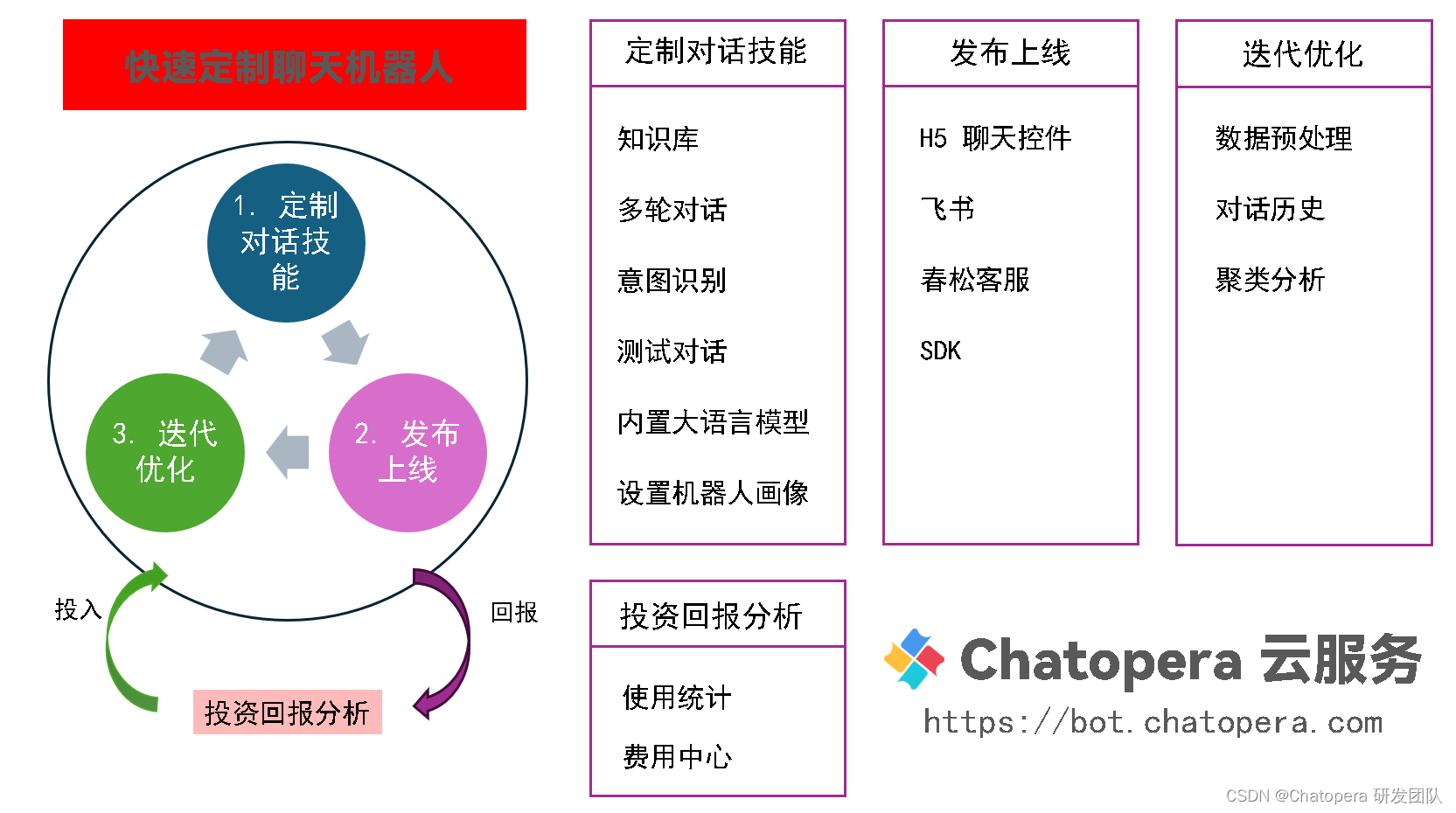
上传文件生成聊天机器人,实现客服、办公自动化智能体 | Chatopera
从谈论聊天机器人,到谈论智能体,是目前人工智能最炙手可热的话题,这两年最大的变化是大语言模型的应用。聊天机器人曾经很难定制,往往局限于个别行业,同时也只有行业内的领导者、头部企业能定制。比如银行、金融证券、…...
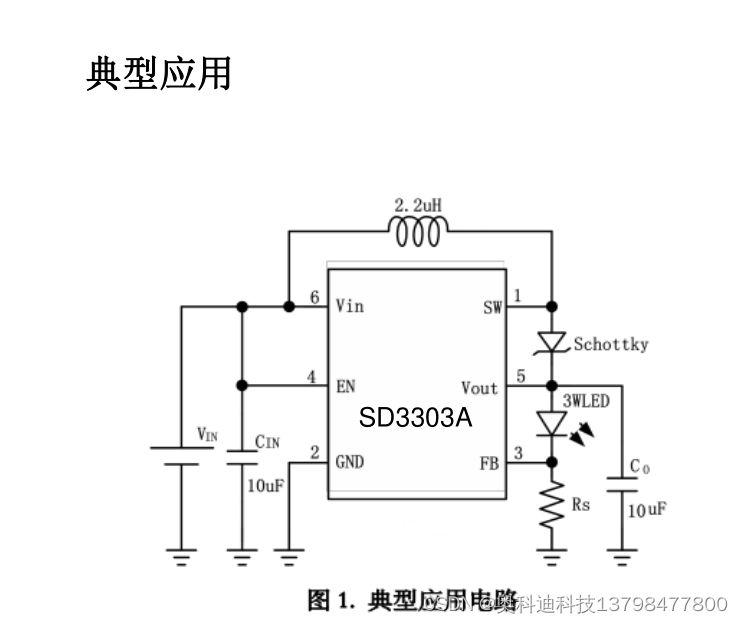
SD3303A 大功率高亮度LED驱动芯片IC
一般描述 SD3303A是一款大功率高亮度LED驱动芯片,可以提供1A的电流驱动3W的LED。具有高效率,低功耗等特点,适用于电池供电的LED照明设备。 SD3303A具有开路保护和过温保护。 SD3303A需要使用两颗10uF(或者更大)的瓷片电容,来保…...

站易WordPress
站易WordPress是一家专业提供网站建设和运营服务的公司。他们提供的服务包括企业官方网站建设、网站运营维护、网站托管、网站优化、跨境独立站建站、外贸网站建设以及海外多语言网站建设等。 此外,站易还提供使用现成的WordPress模板,这样可以快速且低…...

windows下JDK1.8安装
windows下JDK1.8安装 本文假设你知道了解基本的windows系统操作。 在Windows系统下安装JDK 1.8(Java Development Kit)的步骤如下: 步骤1:下载JDK 1.8 打开浏览器并访问Oracle JDK下载页面。https://www.oracle.com/java/technol…...
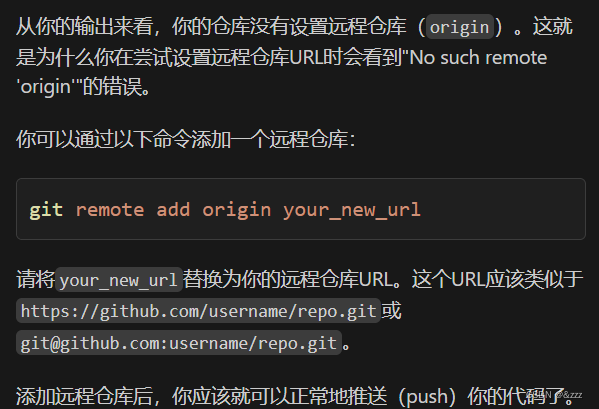
怎么修改Visual Studio Code中现在github账号
git config --global user.name “你的用户名” git config --global user.email “你的邮箱” git config --global --list git push -u origin your_branch_name git remote add origin...

戴尔R720服务器(3)组RAID
今天收到7块硬盘,现在共有8块硬盘了,找了个视频学习了怎么使用阵列卡组RAID并记录。 视频参考:【戴尔服务器添加RAID5热备盘hotspare】 阵列卡组RAID5 开始 连接iDRAC控制台服务器开机按F2进入BIOS选择Device Settings …...
eNSP学习——配置高级的访问控制列表
目录 主要命令 原理概述 实验目的 实验内容 实验拓扑 实验编址 实验步骤 1、基本配置 2、搭建OSPF网络 3、配置Telnet 4、配置高级ACL控制访问 需要eNSP各种配置命令的点击链接自取:华为eNSP各种设备配置命令大全PDF版_ensp配置命令大全资源-…...

oracle的bitmap索引是什么
Oracle的Bitmap索引是一种特殊的索引类型,主要用于处理那些数值稀疏(low-cardinality,低基数)的字段,特别是那些值不经常改变的字段。以下是关于Bitmap索引的详细解释: 定义: Bitmap索引是一种…...

「前端+鸿蒙」鸿蒙应用开发-TS接口-特殊用途
在 TypeScript 中,接口除了定义对象的结构之外,还有一些特殊用途,这些用途使得接口成为一种灵活的工具,用于提高代码的可维护性和可扩展性。 TS快速入门-接口-特殊用途 1. 定义函数类型 接口可以用来定义函数的类型,…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

内窥镜检查中基于提示的息肉分割|文献速递-深度学习医疗AI最新文献
Title 题目 Prompt-based polyp segmentation during endoscopy 内窥镜检查中基于提示的息肉分割 01 文献速递介绍 以下是对这段英文内容的中文翻译: ### 胃肠道癌症的发病率呈上升趋势,且有年轻化倾向(Bray等人,2018&#x…...

大数据驱动企业决策智能化的路径与实践
📝个人主页🌹:慌ZHANG-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、引言:数据驱动的企业竞争力重构 在这个瞬息万变的商业时代,“快者胜”的竞争逻辑愈发明显。企业如何在复杂环…...

算法刷题-回溯
今天给大家分享的还是一道关于dfs回溯的问题,对于这类问题大家还是要多刷和总结,总体难度还是偏大。 对于回溯问题有几个关键点: 1.首先对于这类回溯可以节点可以随机选择的问题,要做mian函数中循环调用dfs(i&#x…...

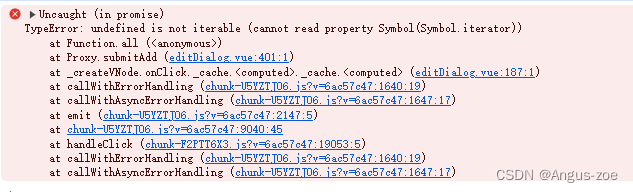
__VUE_PROD_HYDRATION_MISMATCH_DETAILS__ is not explicitly defined.
这个警告表明您在使用Vue的esm-bundler构建版本时,未明确定义编译时特性标志。以下是详细解释和解决方案: 问题原因: 该标志是Vue 3.4引入的编译时特性标志,用于控制生产环境下SSR水合不匹配错误的详细报告1使用esm-bundler…...
)
使用python进行图像处理—图像滤波(5)
图像滤波是图像处理中最基本和最重要的操作之一。它的目的是在空间域上修改图像的像素值,以达到平滑(去噪)、锐化、边缘检测等效果。滤波通常通过卷积操作实现。 5.1卷积(Convolution)原理 卷积是滤波的核心。它是一种数学运算,…...
