平移矩阵中的数学思考
《webgl编程指南》中,“平移矩阵”中相关值的得出
是基于“矩阵和向量相乘所得的等式”与“向量表达式”组成一个方程组
x'=ax+by+cz+d
x'=x+Tx
书中说,根据上面的方程组,可以很容易得出
a=1、b=0、c=0、d=Tx
0、问题来了!
我也确实可以看出,a=1、b=0、c=0、d=Tx,是上述方程组的一个解
但是,我觉得这种方式很不“数学”!很不“严谨”!!
也没有用严谨的手段来证明,只有这1个解!!(我这篇文章也没有证明)
下面写出自己的一些思考和推导过程
1、定义和概念:
正确的定义和概念,就可以极大的推进问题的解决
上述方程组中,我觉得有这么几类数据:
| 类型 | 相关变量 | 备注 |
| “自由”变量 | x、y、z、x' | 可以随意赋值为任何数 |
| 未知常量 | a、b、c、d | 要解出“未知常量” |
| 已知常量 | Tx | 可以当做一个已知常数来对待 |
2、取值互相不约束
上述方程中x、y、z的取值,是互相不限制
(x想取什么值,就取什么值,不需要考虑y或z是什么值)
备注:
下述方程组中,x、y的值就是互相制约和限制(x想取什么值,需要考虑y已经取了什么值)
23x+17y=63
17x+23y=57
3、方案1:
基于1的结论,我可以随便给出x、y、z的值
给出4组值,就会组成4个等式,然后求4个“未知常量”
4、方案2:
因为x、y、z可以取任意值,可以取一个特殊值,比如0
来快速求解出“未知常量”
把上述方程组,改成等式:ax+by+cz+d=x+Tx
情形A:x=0;y=0;z=0;
带入等式:0a+0b+0c+d=0+Tx
结果:d=Tx
情形B:x=0;y=0;z=1;
带入等式:0a+0b+1c+d=0+Tx
结果:c=Tx-d
因为:Tx=d
所以:c=0
情形C:x=0;y=1;z=0;
带入等式:0a+1b+0c+d=0+Tx
结果:b=0
情形D:x=1;y=0;z=0;
带入等式:1a+0b+0c+d=1+Tx
结果:a=1
至此:
才算严格的证明了:
a=1、b=0、c=0、d=Tx是方程的一个解!
(数学水平一般,不知道这个推导对不对,欢迎大家指正)
相关文章:

平移矩阵中的数学思考
《webgl编程指南》中,“平移矩阵”中相关值的得出 是基于“矩阵和向量相乘所得的等式”与“向量表达式”组成一个方程组 xaxbyczd xxTx 书中说,根据上面的方程组,可以很容易得出 a1、b0、c0、dTx 0、问题来了! 我也确实可以看…...
【机器学习】Qwen2大模型原理、训练及推理部署实战
目录 一、引言 二、模型简介 2.1 Qwen2 模型概述 2.2 Qwen2 模型架构 三、训练与推理 3.1 Qwen2 模型训练 3.2 Qwen2 模型推理 四、总结 一、引言 刚刚写完【机器学习】Qwen1.5-14B-Chat大模型训练与推理实战 ,阿里Qwen就推出了Qwen2&#x…...
JetLinks开源物联网平台社区版部署教程
1.上github搜素jetlinks 2.找到源代码,并且下载到本地。 3.项目下载完成之后,还需要另外下载三个核心依赖模块。在github找到jetlinks。 4.点击进去下载,下载完成之后,你会发现里面有三个文件夹是空白的,先不用理会&am…...
QT学习过程中遇到的问题自记
文章目录 前言问题1问题2问题3 前言 学习QT嵌入式实战开发(从串口通信到JSON通信微课视频版)的过程中遇到的几个小问题 问题1 1.将书中的示例代码导入自己的电脑,然后点击工程进去,不能运行,报错 no kits are enabled for this project… 我…...

自学网络安全的三个必经阶段(含路线图)
一、为什么选择网络安全? 这几年随着我国《国家网络空间安全战略》《网络安全法》《网络安全等级保护2.0》等一系列政策/法规/标准的持续落地,网络安全行业地位、薪资随之水涨船高。 未来3-5年,是安全行业的黄金发展期,提前踏入…...

gitlab下载及安装
目录 1、gitlab下载 2、gitlab安装 3、完全卸载GitLab 1、gitlab下载 首页:https://about.gitlab.com 安装:https://about.gitlab.com/install rpm包:https://packages.gitlab.com/gitlab/gitlab-ce 2、gitlab安装 2.1 CentOS 7 rpm -iv…...

YOLOv10改进|采用ADown降采样模块有效融合
📚 专栏地址:《YOLOv10算法改进实战》 👉 独家改进,对现有YOLOv10进行二次创新,提升检测精度,适合科研创新度十足,强烈推荐 🌟 统一使用 YOLOv10 代码框架,结合不同模块来构建不同的YOLO目标检测模型。 💥 本博客包含大量的改进方式,降低改进难度,改进点包含【B…...

libGL.so.1: cannot open shared object file: No such file or directory
Ubuntu 安装 PaddleOCR 时报错 libGL.so.1: cannot open shared object file: No such file or directory解决办法: # 这个好像GPU 服务器更好用 pip install opencv-python-headless如果不行就: # 尝试安装缺失的libGL.so.1文件。在大多数Linux发行版…...

2024年消防设施操作员考试题库及答案
一、单选题 31.工作时间是指劳动者根据国家的法律规定,在1个昼夜或1周之内从事本职工作的时间。《劳动法》规定劳动者每日工作时间不超过8h,平均每周工作时间不超过()h。 A.44 B.45 C.46 D.50 答案:A 解析&…...

30字以内免费翻译维吾尔语,汉维翻译工具推荐,维吾尔文字母OCR识别神器《维汉翻译通》App!
维吾尔文OCR文字识别 《维汉翻译通》App内置的OCR技术,能够快速识别图片中的文字和字母,无论是路标、菜单还是书籍,都能迅速转换为用户所需的语言,让语言障碍不再是问题。针对维吾尔语更是进行了专门的优化,即便是手写…...

省市县选择三级联动(使用高德API实现)
省市县选择如果自己实现是比较麻烦的,最近发现可以使用高德实现省市县联动选择,实现后来记录一下供大家参考。 文章目录 最终效果:一、准备工作二、完整页面代码 最终效果: 实现单次点击获取省市县名称,选择完成后返回…...

【数据结构(邓俊辉)学习笔记】图06——最小支撑树
文章目录 0. 概述1. 支撑树2. 最小支撑树3. 歧义性4. 蛮力算法5. Prim算法5.1 割与极短跨越边5.2 贪心迭代5.3 实例5.4 实现5.5 复杂度 0. 概述 学习下最小支撑树和prim算法。 1. 支撑树 最小的连通图是树。 连通图G的某一无环连通子图T若覆盖G中所有的顶点,则称…...

海豚调度清理:使用 API 轻松清理历史工作流实例以及日志文件
💡 本系列文章是 DolphinScheduler 由浅入深的教程,涵盖搭建、二开迭代、核心原理解读、运维和管理等一系列内容。适用于想对 DolphinScheduler了解或想要加深理解的读者。 祝开卷有益。 大数据学习指南 大家好,我是小陶,DolphinS…...

python怎么显示行号
我们如果想让Python IDLE显示行号,我们可以通过扩展IDLE功能来做到。 1.我们需要下载一个LineNumber.py扩展。 2.我们打开Python安装目录,找到安装目录下的Lib\idlelib目录,复制LineNumber到这个目录。 3.然后启动扩展。 4.配置扩展的方式…...

pytorch中,load_state_dict和torch.load的区别?
在 PyTorch 中,load_state_dict 和 torch.load 是两个不同的函数,用于不同的目的。 torch.load: 用途: 从磁盘加载一个保存的对象。这个对象可以是一个模型的整个状态字典(包含模型参数)、优化器状态字典、甚至是任意其他 Python …...
)
ObjectARX打印当前图纸为PDF,无延迟(亲测有效)
CAD二次开发定制ObjectARX安装配置AutoCAD插件ZWCAD插件C++ //----------------------------------------------------------------------------- //----- acrxEntryPoint.cpp //----------------------------------------------------------------------------- #include &quo…...
 dim=1 dim=-1 dim=2)
torch.squeeze() dim=1 dim=-1 dim=2
对数据的维度进行压缩 使用方式:torch.squeeze(input, dimNone, outNone) 将输入张量形状中的1 去除并返回。 如果输入是形如(A1B1C1D),那么输出形状就为: (ABCD) import torch x torch.rand(2, 1, 1, 3, 1, 4) print(x) print(x.shape) …...

智慧环保一体化平台简介
据悉,环保问题日益受到人们的关注,智慧环保一体化平台作为解决环保问题的有力工具,正逐渐走进人们的视野。朗观视觉智慧环保一体化平台通过整合各类环保资源,实现环境数据的实时监测、分析与管理,为环境保护提供智能化…...
idea在空工程中添加新模块并测试的步骤
ServicesTest是空的工程,没有pom文件。现在需要在ServicesTest目录下添加新模块作为新的工程,目的是写一下别的技术功能。 原先目录结构,ServicesTest是空的工程,没有pom文件。下面的几个模块是新的工程,相互独立。 1.…...
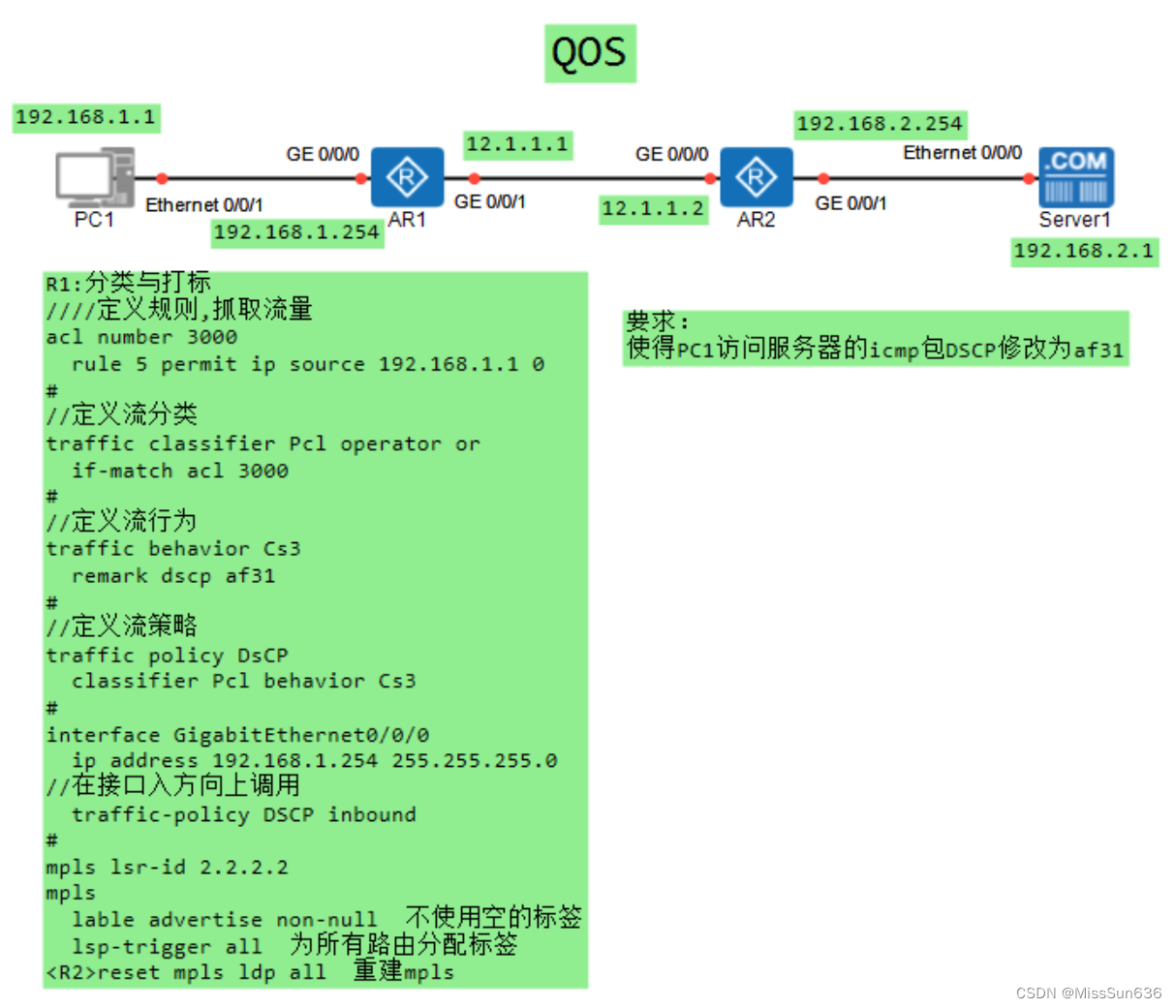
HCIE-QOS基本原理
QOS基本原理 QOS概述什么是QOSQoS服务模型区分服务模型QoS常用技术 (DiffServ模型)QoS数据处理流程 (DiffServ模型) QoS流分类和流标记QoS数据处理流程为什么需要流分类和流标记 简单流分类外部优先级 - VLAN报文外部优先级 - MPLS报文外部优先级 - IP报文各外部优先级间的对应…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...
