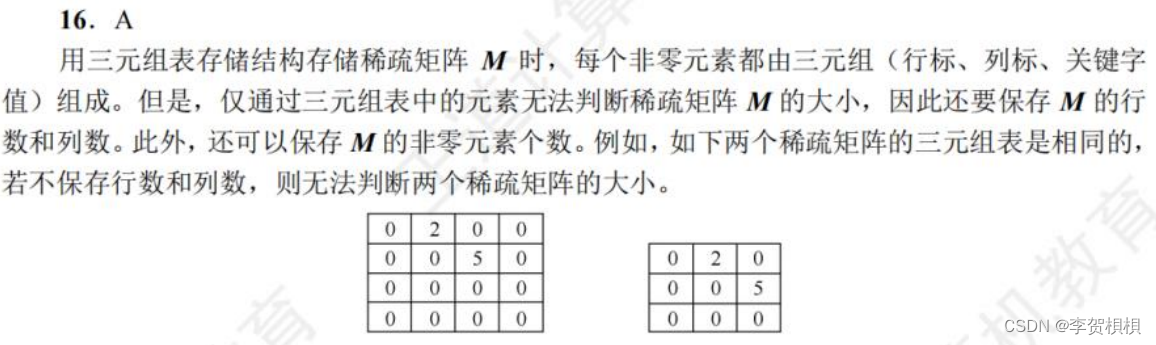
数据结构错题答案汇总
王道学习
第一章 绪论
1.1
3.A
数据的逻辑结构是从面向实际问题的角度出发的,只采用抽象表达方式,独立于存储结构,数据的存储方式有多种不同的选择;而数据的存储结构是逻辑结构在计算机上的映射,它不能独立于逻辑结构而存在。数据结构包括三个要素,缺一不可。
解:应该注意到,数据的运算也是数据结构的一个重要方面。
对于两种不同的数据结构,它们的逻辑结构和物理结构完全有可能相同。比如二叉树和二叉排序树,二叉排序树可以采用二叉树的逻辑表示和存储方式,前者通常用于表示层次关系,而后者通常用于排序和查找。虽然它们的运算都有建立树、插入结点、/删除结点和查找结点等功能,但对于二叉树和二叉排序树,这些运算的定义是不同的,以查找结点为例,二叉树的时间复杂度为O(n)而二叉排序树的时间复杂度为O(logn)。
解:线性表既可以用顺序存储方式实现,又可以用链式存储方式实现。在顺序存储方式下,在线性表中插入和删除元素,平均要移动近一半的元素,时间复杂度为O(n);而在链式存储方式下.插入和删除的时间复杂度都是O(1)。
1.2

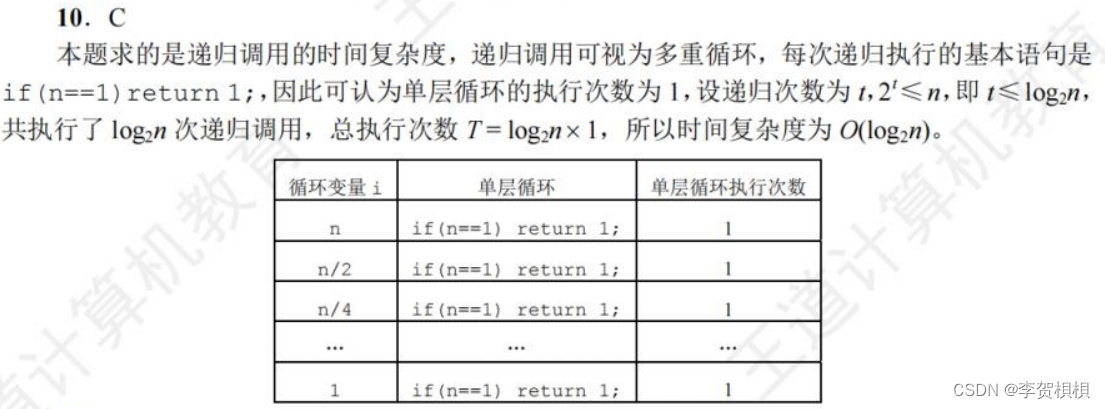
第10题主要是判断递归的次数。当n=1时,没有递归;当n=2时,递归了1次;当n=4时,递归了2次。所以选C。

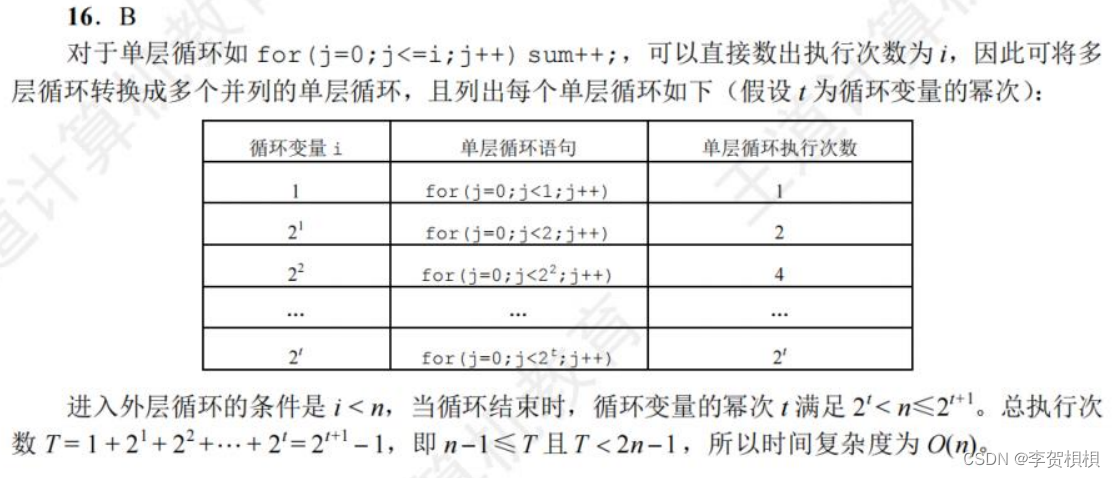
第16题可以采用举例的方法,当n=2时,sum++运行1次;当n=4时,sum++运行3次;当n=8时,sum++运行7次。所以选B

第二章 线性表
2.1
答案:B
线性表定义的要求为:相同数据类型、有限序列。选项C的元素个数是无穷个,错误;选项A集合中的元素没有前后驱关系,错误;选项D属于存储结构
2.2

第三章 栈、队列和数组
3.1

3.2

第8题可以考虑特殊情况:当队列中只剩下一个元素,考虑此情况就知道答案了。

第10题可以考虑特殊情况:当队列中只剩下一个元素。


第14题考考虑删除的方便性:如果队头在链尾和链中,出队时需要遍历链表;

第21题:rear有两种情况,第一种是rear指向当前的队尾元素;第二种是rear指向队尾元素的下一个位置。
3.3
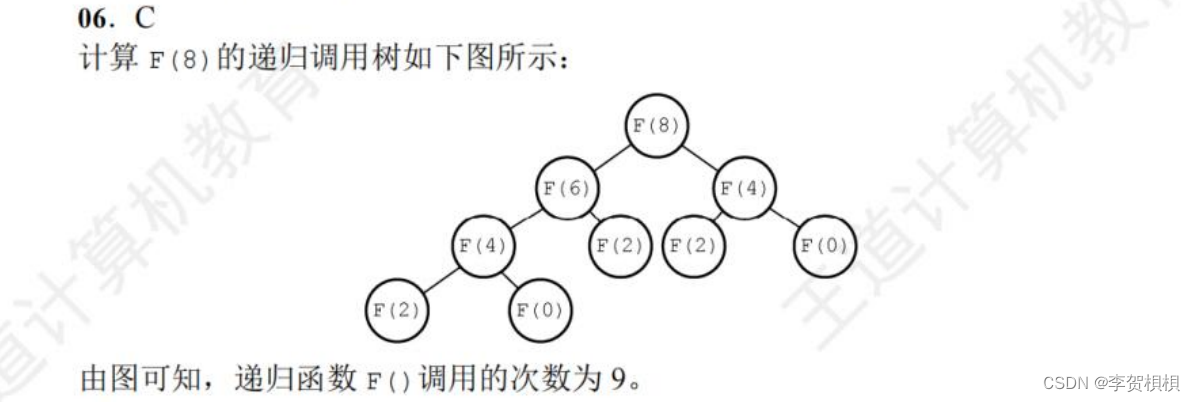


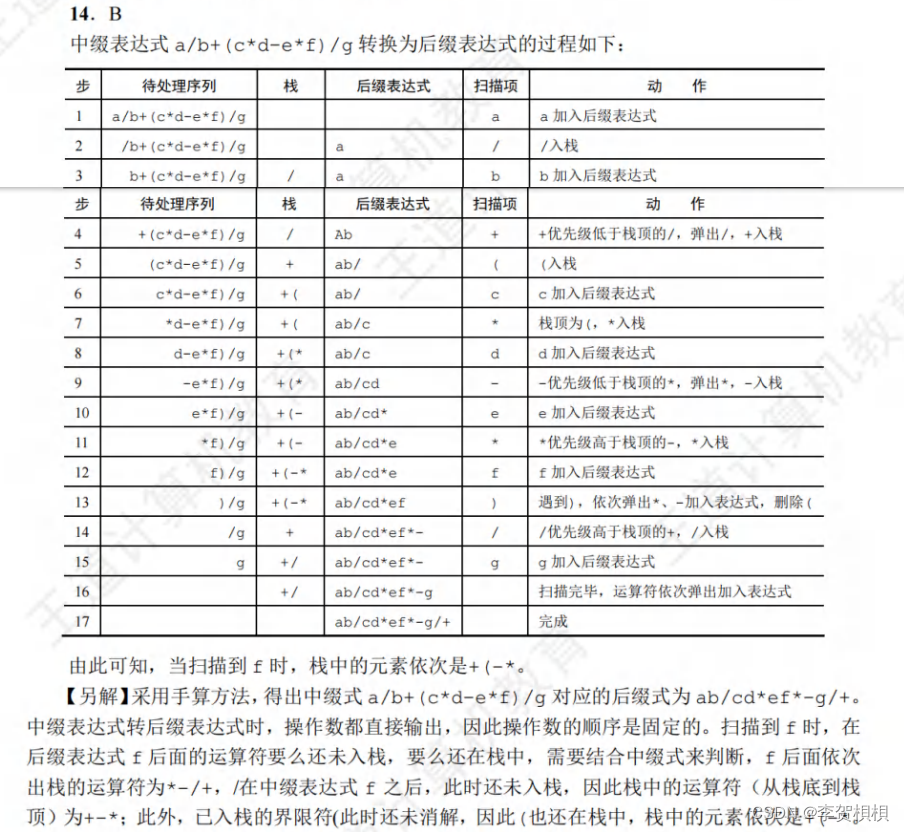
3.4



第四章 串
4.2

相关文章:

数据结构错题答案汇总
王道学习 第一章 绪论 1.1 3.A 数据的逻辑结构是从面向实际问题的角度出发的,只采用抽象表达方式,独立于存储结构,数据的存储方式有多种不同的选择;而数据的存储结构是逻辑结构在计算机上的映射,它不能独立于逻辑结构而存在。数…...

搞AI?中小企业拿什么和大厂拼?
近期,苹果发布M4芯片,号称“比当今任何AI PC的任何神经引擎都强!”紧随其后微软携“CopilotPCs”的概念加入AI PC激战。截至目前,包括联想、惠普、华为等多家主流PC厂商在内,已经至少推出了超50款AI PC产品。 AI重塑行…...

光伏电站阵列式冲击波声压光伏驱鸟器
光伏电站内鸟群的聚集可不是一件好事,鸟类排泄物,因其粘度大、具有腐蚀性的特点,一旦堆积在太阳能板上,会严重影响光伏电站的发电效率。长期积累的鸟粪不仅难以清洗,还可能引发组件的热斑效应,严重时甚至可…...
)
Webrtc支持FFMPEG硬解码之解码实现(三)
前言 此系列文章分分为三篇, Webrtc支持FFMPEG硬解码之Intel(一)-CSDN博客 Webrtc支持FFMPEG硬解码之NVIDA(二)-CSDN博客 Webrtc支持FFMPEG硬解码之解码实现(三)-CSDN博客 AMD硬解目前还没找到可用解码器,欢迎留言交流 环境 Windows平台 VS2019 <...

RIP协议
RIP基本概念 RIP(Routing Information Protocol)是一种基于距离矢量的路由协议,用于在自治系统(AS)内的网关之间交换路由信息。RIP 是一种相对简单且广泛使用的内部网关协议(IGP),适…...

计算机视觉与深度学习实战,Python为工具,基于光流场的车流量计数应用
一、引言 随着科技的飞速发展,计算机视觉和深度学习技术在现代社会中的应用越来越广泛。其中,车流量计数作为智能交通系统的重要组成部分,对于城市交通管理和规划具有重要意义。本文旨在探讨以Python为工具,基于光流场的车流量计数应用,为智能交通系统的发展提供技术支撑。…...
)
插入排序(排序算法)
文章目录 插入排序详细代码 插入排序 插入排序,类似于扑克牌的玩法一样,在有序的数组中,扫描无序的数组,逐一的将元素插入到有序的数组中。 实现细节: 从第一个元素开始,该元素可以认为已经被排序取出下…...
、第三个demo -机械臂的避障规划)
【附带源码】机械臂MoveIt2极简教程(六)、第三个demo -机械臂的避障规划
系列文章目录 【附带源码】机械臂MoveIt2极简教程(一)、moveit2安装 【附带源码】机械臂MoveIt2极简教程(二)、move_group交互 【附带源码】机械臂MoveIt2极简教程(三)、URDF/SRDF介绍 【附带源码】机械臂MoveIt2极简教程(四)、第一个入门demo 【附带源码】机械臂Move…...

innovus:route secondary pg pin
我正在「拾陆楼」和朋友们讨论有趣的话题,你⼀起来吧? 拾陆楼知识星球入口 innovus route secondary pg pin分以下几步: #设置pg net连接 globalNetConnect VDD_AON -type pgpin -pin VNW #设置ndr rule,具体绕线层次跟signal绕…...

btstack协议栈实战篇--LE Peripheral - Test Pairing Methods
btstack协议栈---总目录_bt stack是什么-CSDN博客 目录 1.Main Application Setup 2.Packet Handler 3.btstack_main 4.log信息 首先先理解一下,ble中的central,Peripheral,master和slave的理解? 以下是对这些概念的理解: “Central”(中心设备):与“Maste…...
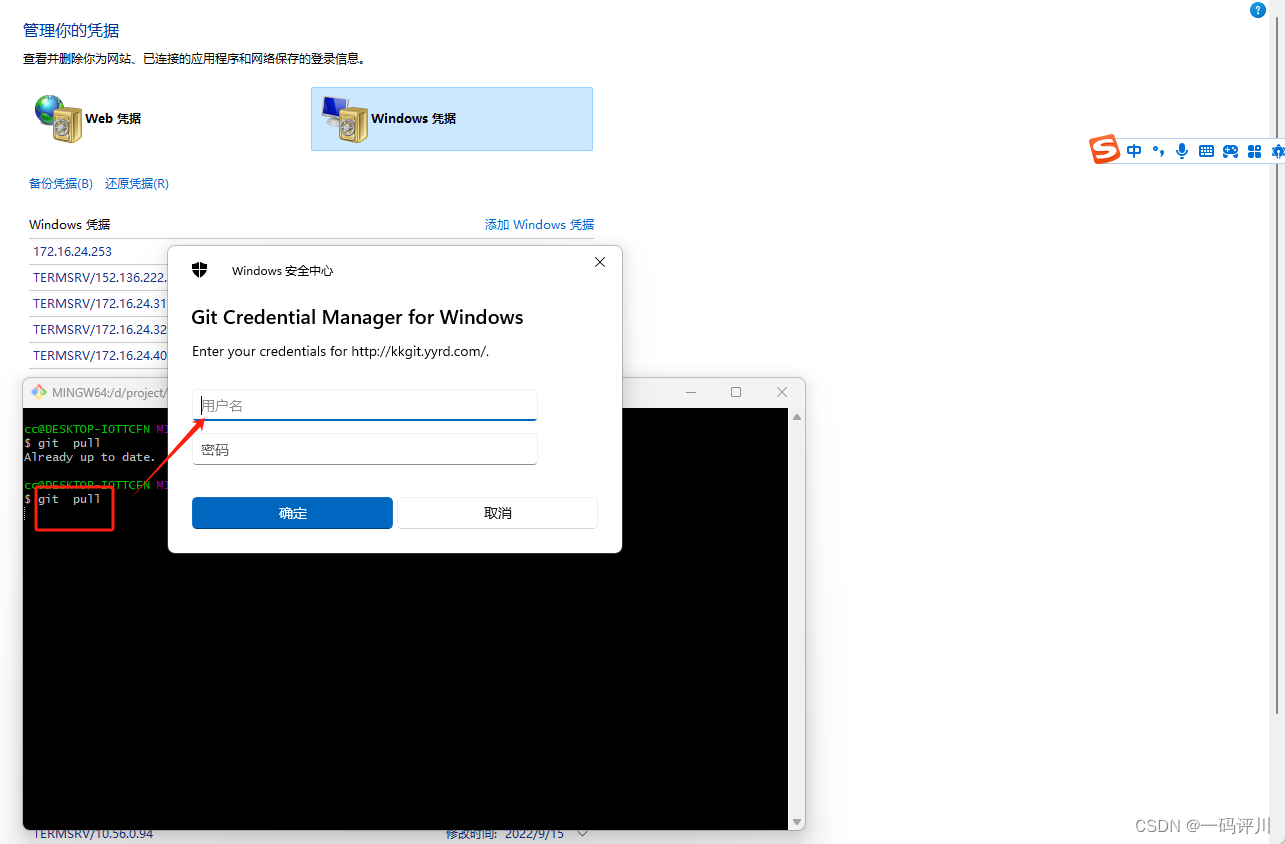
git下载项目登录账号或密码填写错误不弹出登录框
错误描述 登录账号或密码填写错误不弹出登录框 二、解决办法 控制面板\用户帐户\凭据管理器 找到对应的登录地址进行更新或者删除 再次拉取或者更新就会提示输入登录信息...

平移矩阵中的数学思考
《webgl编程指南》中,“平移矩阵”中相关值的得出 是基于“矩阵和向量相乘所得的等式”与“向量表达式”组成一个方程组 xaxbyczd xxTx 书中说,根据上面的方程组,可以很容易得出 a1、b0、c0、dTx 0、问题来了! 我也确实可以看…...
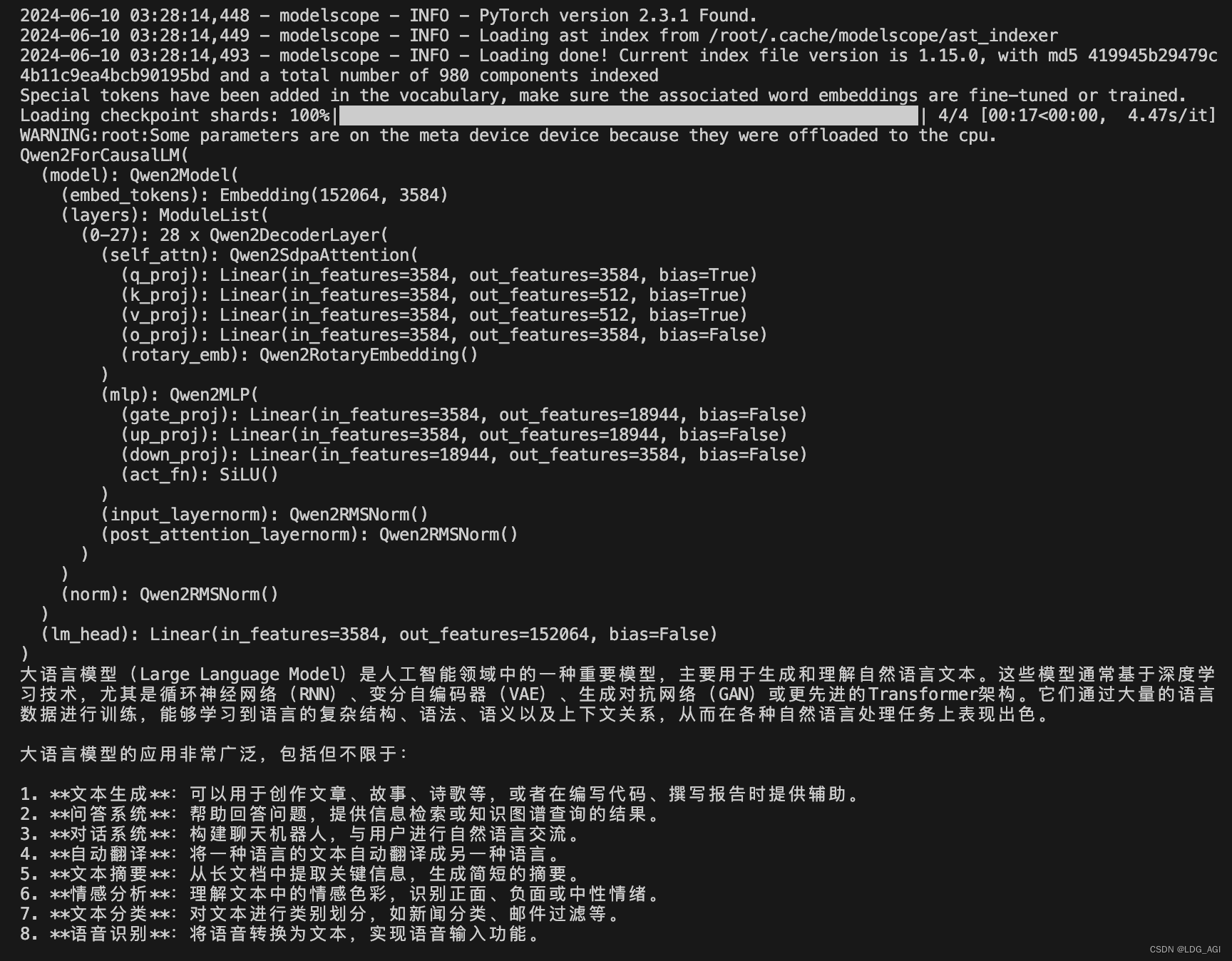
【机器学习】Qwen2大模型原理、训练及推理部署实战
目录 一、引言 二、模型简介 2.1 Qwen2 模型概述 2.2 Qwen2 模型架构 三、训练与推理 3.1 Qwen2 模型训练 3.2 Qwen2 模型推理 四、总结 一、引言 刚刚写完【机器学习】Qwen1.5-14B-Chat大模型训练与推理实战 ,阿里Qwen就推出了Qwen2&#x…...
JetLinks开源物联网平台社区版部署教程
1.上github搜素jetlinks 2.找到源代码,并且下载到本地。 3.项目下载完成之后,还需要另外下载三个核心依赖模块。在github找到jetlinks。 4.点击进去下载,下载完成之后,你会发现里面有三个文件夹是空白的,先不用理会&am…...
QT学习过程中遇到的问题自记
文章目录 前言问题1问题2问题3 前言 学习QT嵌入式实战开发(从串口通信到JSON通信微课视频版)的过程中遇到的几个小问题 问题1 1.将书中的示例代码导入自己的电脑,然后点击工程进去,不能运行,报错 no kits are enabled for this project… 我…...

自学网络安全的三个必经阶段(含路线图)
一、为什么选择网络安全? 这几年随着我国《国家网络空间安全战略》《网络安全法》《网络安全等级保护2.0》等一系列政策/法规/标准的持续落地,网络安全行业地位、薪资随之水涨船高。 未来3-5年,是安全行业的黄金发展期,提前踏入…...

gitlab下载及安装
目录 1、gitlab下载 2、gitlab安装 3、完全卸载GitLab 1、gitlab下载 首页:https://about.gitlab.com 安装:https://about.gitlab.com/install rpm包:https://packages.gitlab.com/gitlab/gitlab-ce 2、gitlab安装 2.1 CentOS 7 rpm -iv…...

YOLOv10改进|采用ADown降采样模块有效融合
📚 专栏地址:《YOLOv10算法改进实战》 👉 独家改进,对现有YOLOv10进行二次创新,提升检测精度,适合科研创新度十足,强烈推荐 🌟 统一使用 YOLOv10 代码框架,结合不同模块来构建不同的YOLO目标检测模型。 💥 本博客包含大量的改进方式,降低改进难度,改进点包含【B…...

libGL.so.1: cannot open shared object file: No such file or directory
Ubuntu 安装 PaddleOCR 时报错 libGL.so.1: cannot open shared object file: No such file or directory解决办法: # 这个好像GPU 服务器更好用 pip install opencv-python-headless如果不行就: # 尝试安装缺失的libGL.so.1文件。在大多数Linux发行版…...

2024年消防设施操作员考试题库及答案
一、单选题 31.工作时间是指劳动者根据国家的法律规定,在1个昼夜或1周之内从事本职工作的时间。《劳动法》规定劳动者每日工作时间不超过8h,平均每周工作时间不超过()h。 A.44 B.45 C.46 D.50 答案:A 解析&…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...
