插入排序(排序算法)
文章目录
- 插入排序
- 详细代码
插入排序
插入排序,类似于扑克牌的玩法一样,在有序的数组中,扫描无序的数组,逐一的将元素插入到有序的数组中。
实现细节:
- 从第一个元素开始,该元素可以认为已经被排序
- 取出下一个元素,已经排序的元素序列中从后向前扫描,逐一的插入到有序数组中。
- 如果有序数组的元素(已排序)大于新元素,将该元素移到下一位置
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位。
- 将新元素插入到该位置中
详细代码
package sort;/*** 作者:Hui* 时间:2024-06-06*//***** @author: Hui**/
public class InsertSort {public static void main(String[] args) {//初始化数组int[] arr = {1, 5, 3, 456, 5, 6, 7, 13, 9, 100};System.out.println("排序前:" );for (int i = 0; i < arr.length; i++) {System.out.println(arr[i]);}InsertSort insertSort = new InsertSort();insertSort.insertSortMethod(arr);System.out.println("排序后:" );for (int i = 0; i < arr.length; i++) {System.out.println(arr[i]);}}//插入排序,类似于扑克牌的玩法一样// 1.从第一个元素开始,该元素可以认为已经被排序// 2.取出下一个元素,已经排序的元素序列中从后向前扫描,逐一的插入到有序数组中。// 3.如果有序数组的元素(已排序)大于新元素,将该元素移到下一位置// 4.重复步骤3,直到找到已排序的元素小于或者等于新元素的位。// 5.将新元素插入到该位置中public int[] insertSortMethod(int arr[]){//1.从第一个元素开始,该元素可以认为已经被排序for (int i = 1; i < arr.length; i++) {int temp = arr[i];int j = i;while (j > 0 && temp < arr[j -1]){ //该元素(已排序)大于新元素arr[j] = arr[j - 1]; //将该元素移到下一位置j--;}if (j != i){arr[j] = temp; //5.将新元素插入到该位置中}}return null;}
}我是小辉,24 届毕业生。当下是找工作ing,欢迎关注,持续分享。
相关文章:
)
插入排序(排序算法)
文章目录 插入排序详细代码 插入排序 插入排序,类似于扑克牌的玩法一样,在有序的数组中,扫描无序的数组,逐一的将元素插入到有序的数组中。 实现细节: 从第一个元素开始,该元素可以认为已经被排序取出下…...
、第三个demo -机械臂的避障规划)
【附带源码】机械臂MoveIt2极简教程(六)、第三个demo -机械臂的避障规划
系列文章目录 【附带源码】机械臂MoveIt2极简教程(一)、moveit2安装 【附带源码】机械臂MoveIt2极简教程(二)、move_group交互 【附带源码】机械臂MoveIt2极简教程(三)、URDF/SRDF介绍 【附带源码】机械臂MoveIt2极简教程(四)、第一个入门demo 【附带源码】机械臂Move…...

innovus:route secondary pg pin
我正在「拾陆楼」和朋友们讨论有趣的话题,你⼀起来吧? 拾陆楼知识星球入口 innovus route secondary pg pin分以下几步: #设置pg net连接 globalNetConnect VDD_AON -type pgpin -pin VNW #设置ndr rule,具体绕线层次跟signal绕…...

btstack协议栈实战篇--LE Peripheral - Test Pairing Methods
btstack协议栈---总目录_bt stack是什么-CSDN博客 目录 1.Main Application Setup 2.Packet Handler 3.btstack_main 4.log信息 首先先理解一下,ble中的central,Peripheral,master和slave的理解? 以下是对这些概念的理解: “Central”(中心设备):与“Maste…...
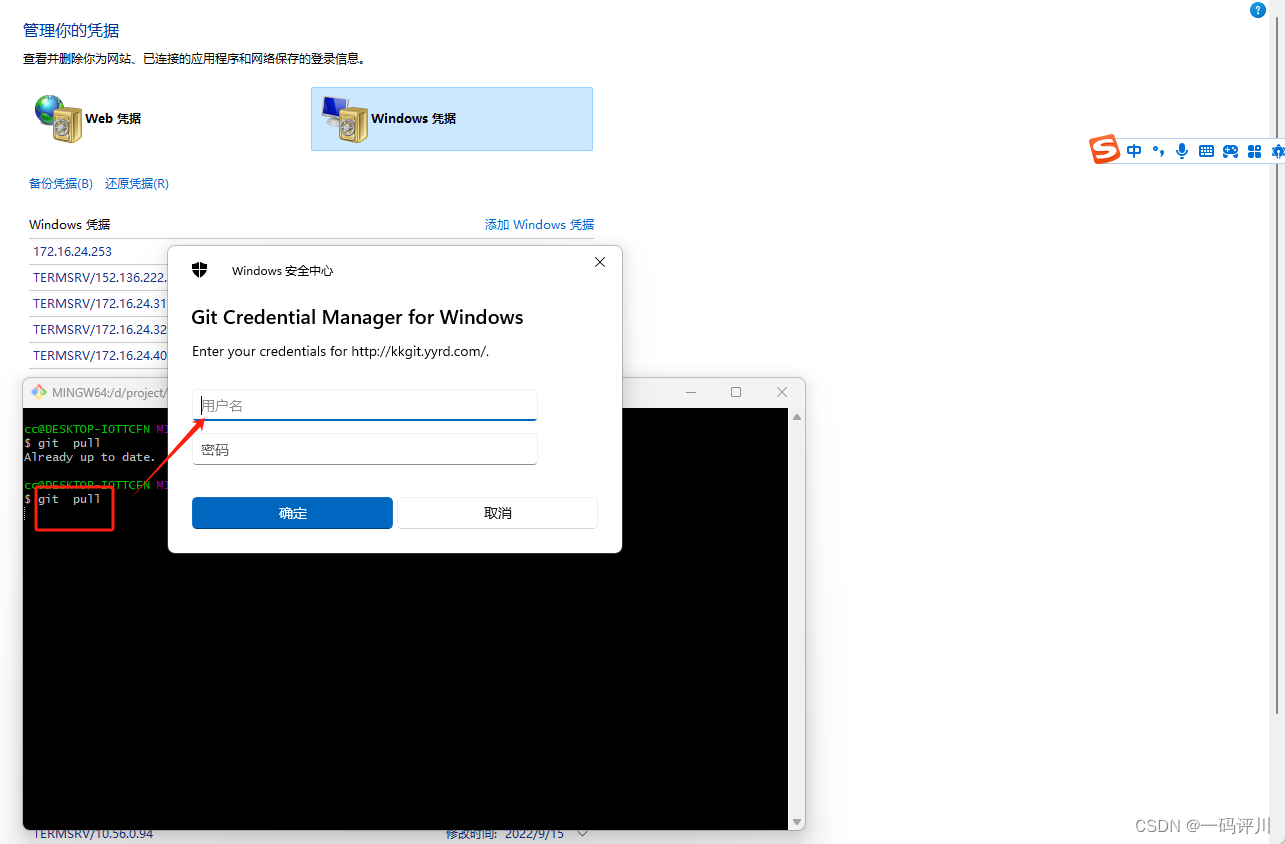
git下载项目登录账号或密码填写错误不弹出登录框
错误描述 登录账号或密码填写错误不弹出登录框 二、解决办法 控制面板\用户帐户\凭据管理器 找到对应的登录地址进行更新或者删除 再次拉取或者更新就会提示输入登录信息...

平移矩阵中的数学思考
《webgl编程指南》中,“平移矩阵”中相关值的得出 是基于“矩阵和向量相乘所得的等式”与“向量表达式”组成一个方程组 xaxbyczd xxTx 书中说,根据上面的方程组,可以很容易得出 a1、b0、c0、dTx 0、问题来了! 我也确实可以看…...
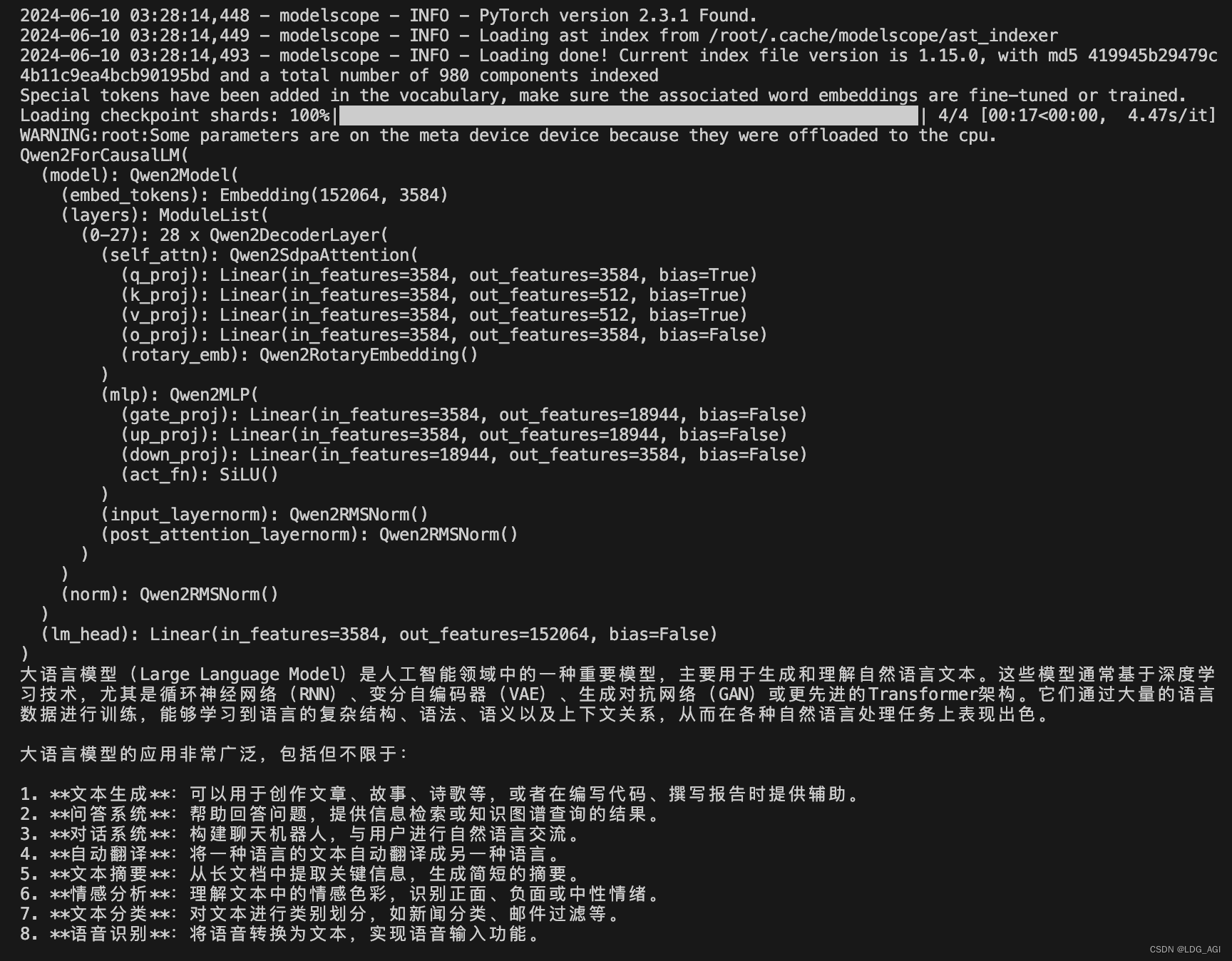
【机器学习】Qwen2大模型原理、训练及推理部署实战
目录 一、引言 二、模型简介 2.1 Qwen2 模型概述 2.2 Qwen2 模型架构 三、训练与推理 3.1 Qwen2 模型训练 3.2 Qwen2 模型推理 四、总结 一、引言 刚刚写完【机器学习】Qwen1.5-14B-Chat大模型训练与推理实战 ,阿里Qwen就推出了Qwen2&#x…...
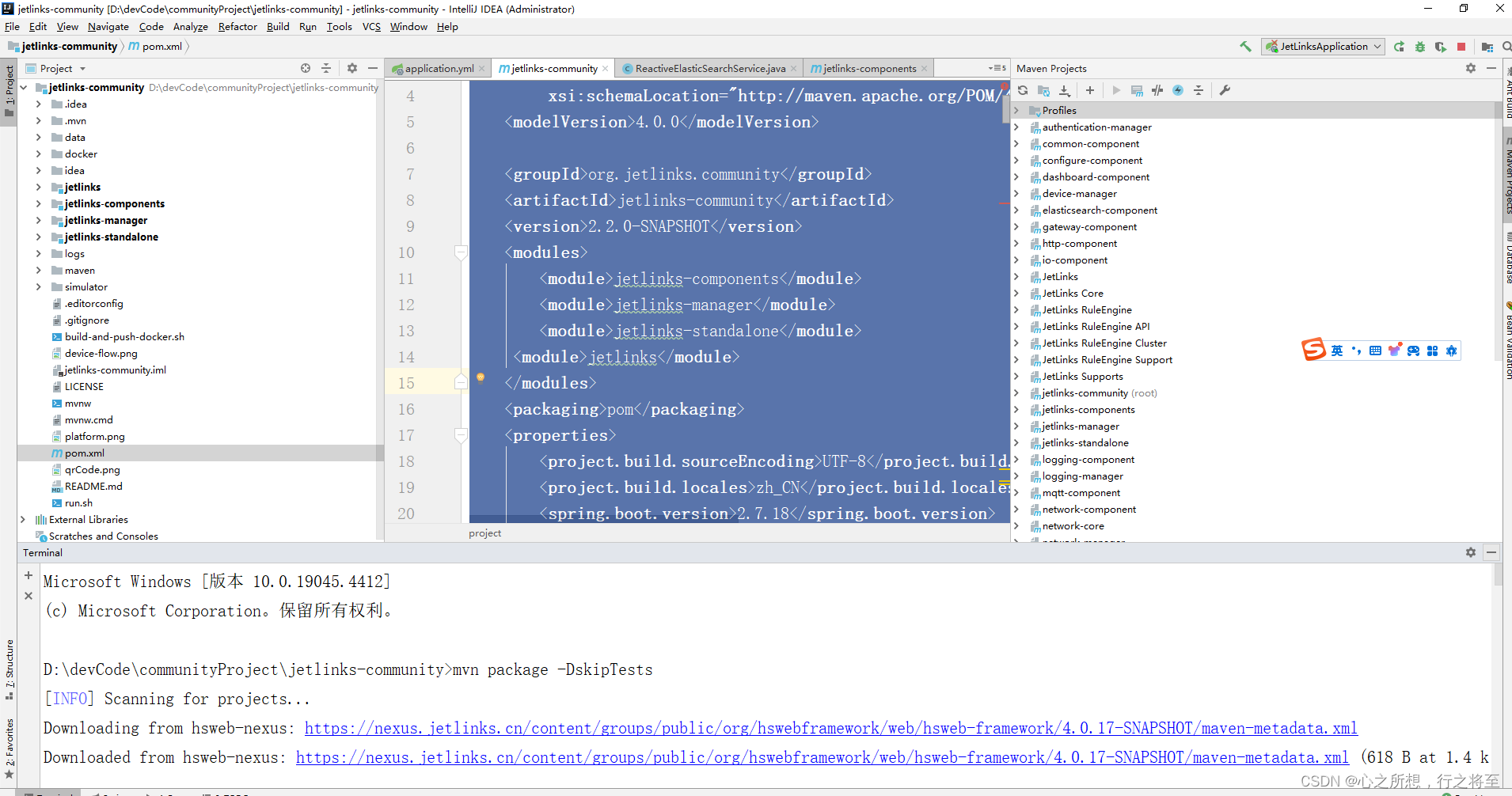
JetLinks开源物联网平台社区版部署教程
1.上github搜素jetlinks 2.找到源代码,并且下载到本地。 3.项目下载完成之后,还需要另外下载三个核心依赖模块。在github找到jetlinks。 4.点击进去下载,下载完成之后,你会发现里面有三个文件夹是空白的,先不用理会&am…...
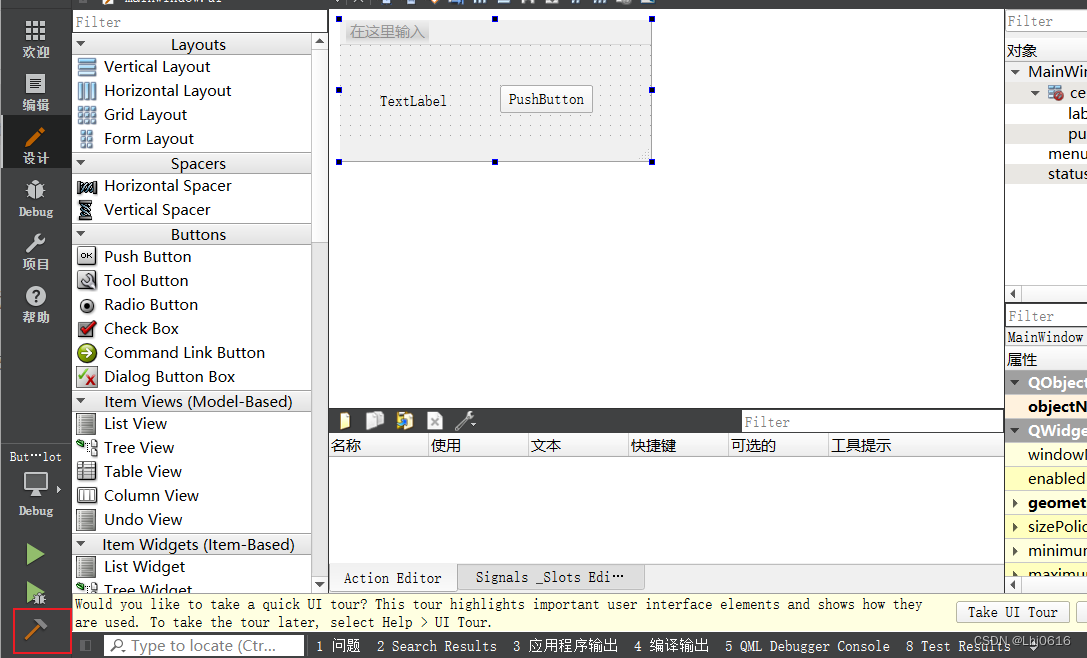
QT学习过程中遇到的问题自记
文章目录 前言问题1问题2问题3 前言 学习QT嵌入式实战开发(从串口通信到JSON通信微课视频版)的过程中遇到的几个小问题 问题1 1.将书中的示例代码导入自己的电脑,然后点击工程进去,不能运行,报错 no kits are enabled for this project… 我…...

自学网络安全的三个必经阶段(含路线图)
一、为什么选择网络安全? 这几年随着我国《国家网络空间安全战略》《网络安全法》《网络安全等级保护2.0》等一系列政策/法规/标准的持续落地,网络安全行业地位、薪资随之水涨船高。 未来3-5年,是安全行业的黄金发展期,提前踏入…...

gitlab下载及安装
目录 1、gitlab下载 2、gitlab安装 3、完全卸载GitLab 1、gitlab下载 首页:https://about.gitlab.com 安装:https://about.gitlab.com/install rpm包:https://packages.gitlab.com/gitlab/gitlab-ce 2、gitlab安装 2.1 CentOS 7 rpm -iv…...

YOLOv10改进|采用ADown降采样模块有效融合
📚 专栏地址:《YOLOv10算法改进实战》 👉 独家改进,对现有YOLOv10进行二次创新,提升检测精度,适合科研创新度十足,强烈推荐 🌟 统一使用 YOLOv10 代码框架,结合不同模块来构建不同的YOLO目标检测模型。 💥 本博客包含大量的改进方式,降低改进难度,改进点包含【B…...

libGL.so.1: cannot open shared object file: No such file or directory
Ubuntu 安装 PaddleOCR 时报错 libGL.so.1: cannot open shared object file: No such file or directory解决办法: # 这个好像GPU 服务器更好用 pip install opencv-python-headless如果不行就: # 尝试安装缺失的libGL.so.1文件。在大多数Linux发行版…...

2024年消防设施操作员考试题库及答案
一、单选题 31.工作时间是指劳动者根据国家的法律规定,在1个昼夜或1周之内从事本职工作的时间。《劳动法》规定劳动者每日工作时间不超过8h,平均每周工作时间不超过()h。 A.44 B.45 C.46 D.50 答案:A 解析&…...

30字以内免费翻译维吾尔语,汉维翻译工具推荐,维吾尔文字母OCR识别神器《维汉翻译通》App!
维吾尔文OCR文字识别 《维汉翻译通》App内置的OCR技术,能够快速识别图片中的文字和字母,无论是路标、菜单还是书籍,都能迅速转换为用户所需的语言,让语言障碍不再是问题。针对维吾尔语更是进行了专门的优化,即便是手写…...

省市县选择三级联动(使用高德API实现)
省市县选择如果自己实现是比较麻烦的,最近发现可以使用高德实现省市县联动选择,实现后来记录一下供大家参考。 文章目录 最终效果:一、准备工作二、完整页面代码 最终效果: 实现单次点击获取省市县名称,选择完成后返回…...

【数据结构(邓俊辉)学习笔记】图06——最小支撑树
文章目录 0. 概述1. 支撑树2. 最小支撑树3. 歧义性4. 蛮力算法5. Prim算法5.1 割与极短跨越边5.2 贪心迭代5.3 实例5.4 实现5.5 复杂度 0. 概述 学习下最小支撑树和prim算法。 1. 支撑树 最小的连通图是树。 连通图G的某一无环连通子图T若覆盖G中所有的顶点,则称…...

海豚调度清理:使用 API 轻松清理历史工作流实例以及日志文件
💡 本系列文章是 DolphinScheduler 由浅入深的教程,涵盖搭建、二开迭代、核心原理解读、运维和管理等一系列内容。适用于想对 DolphinScheduler了解或想要加深理解的读者。 祝开卷有益。 大数据学习指南 大家好,我是小陶,DolphinS…...

python怎么显示行号
我们如果想让Python IDLE显示行号,我们可以通过扩展IDLE功能来做到。 1.我们需要下载一个LineNumber.py扩展。 2.我们打开Python安装目录,找到安装目录下的Lib\idlelib目录,复制LineNumber到这个目录。 3.然后启动扩展。 4.配置扩展的方式…...

pytorch中,load_state_dict和torch.load的区别?
在 PyTorch 中,load_state_dict 和 torch.load 是两个不同的函数,用于不同的目的。 torch.load: 用途: 从磁盘加载一个保存的对象。这个对象可以是一个模型的整个状态字典(包含模型参数)、优化器状态字典、甚至是任意其他 Python …...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...
