css3中有哪些新属性(特性)?
在 CSS3 中引入了许多新的属性和特性,以下是其中一些主要的:
-
Flexbox(弹性盒子布局):通过
display: flex及其相关属性,实现灵活的布局方式,使得元素在容器中可以自动调整大小和位置。 -
Grid(网格布局):通过
display: grid及其相关属性,实现二维网格布局,使得元素可以以行和列的方式进行排列。 -
Transitions(过渡效果):通过
transition属性,实现在状态改变时,元素样式平滑过渡的效果,如颜色、大小、位置等。 -
Animations(动画效果):通过
@keyframes规则和animation属性,实现更复杂的动画效果,可以控制元素的逐帧动画行为。 -
Transforms(变形):通过
transform属性,实现元素的旋转、缩放、倾斜和移动,而无需改变文档布局。 -
Media Queries(媒体查询):通过
@media规则,根据设备或浏览器的特定特性(如宽度、高度、分辨率等)来应用不同的样式。 -
Box Shadow(阴影效果):通过
box-shadow属性,为元素添加阴影效果,可以设置阴影的颜色、大小、模糊度和偏移量。 -
Border Radius(边框圆角):通过
border-radius属性,为元素的边框添加圆角效果,使其边角变得圆滑。 -
Gradient(渐变):通过
linear-gradient和radial-gradient函数,实现背景色的渐变效果,可以创建平滑过渡的色彩效果。 -
Custom Fonts(自定义字体):通过
@font-face规则,引入并使用自定义字体文件(如woff、woff2),使得网页能够显示设计师选择的字体样式。
这些新属性和特性使得开发者能够更加灵活和精确地控制页面的外观和行为,提升用户体验和视觉吸引力。
希望可以帮到大家;
相关文章:
?)
css3中有哪些新属性(特性)?
在 CSS3 中引入了许多新的属性和特性,以下是其中一些主要的: Flexbox(弹性盒子布局):通过 display: flex 及其相关属性,实现灵活的布局方式,使得元素在容器中可以自动调整大小和位置。 Grid&am…...

SAP ABAP 之面向对象OO
文章目录 前言一、类的理解二、如何创建ABAP类 a.类的定义与构成 b.类的访问区域 c.特殊方法 d.类的继承 三、类中参数的使用 a.IMPORTING / EXPORTING b.CHANGING c.RETURNING d.EX…...

在VSCode中使用Vim
在VSCode中使用Vim,主要涉及到Vim插件的安装和配置。以下是在VSCode中使用Vim的详细步骤: 1. 安装Vim插件 打开VSCode:首先,启动你的VSCode编辑器。进入扩展面板:在VSCode的左侧活动栏中,点击扩展图标&am…...
鸿蒙低代码开发的局限性
在版本是DevEco Studio 3.1.1 Release,SDK是3.1.0(API9) 的基础上。 1、低代码插件没有WebView组件。 2、低代码插件没有空白的自定义组件,当前提供的所谓自定义组件,只能用列表中提供的组件来拼接新的组件。 3、使用ets代码自定义的组件&…...
 c++题解(A-H1))
Codeforces Round 952 (Div. 4) c++题解(A-H1)
开头 : 这场没打,今天vp了一下,写了A-G,然后就去吃饭了! 比赛链接 : Dashboard - Codeforces Round 952 (Div. 4) - Codeforces A 直接交换,输出即可 inline void solve(){string a , b ; cin >> a>> b ;char c a[0] ;a…...

人工智能将成为数学家的“副驾驶”
人工智能将成为数学家的“副驾驶” 数学传统上是一门独立的科学。1986年,安德鲁怀尔斯为了证明费马定理,退到书房里呆了7年。由此产生的证明往往很难让同事们理解,有些至今仍有争议。但近年来,越来越多的数学领域被严格地分解为各…...

自适应巡航控制技术规范(简化版)
自适应巡航控制技术规范(简化版) 1 系统概述2 功能需求3 性能需求4 功能激活条件5 功能抑制条件6 系统局限性1 系统概述 ACC 自适应巡航系统可自动控制纵向跟车距离,减轻驾驶员的工作量,即驾驶员无需频繁的踩制动和油门便可完成部分的驾驶任务,但责任主体仍然是驾驶员,驾…...

【AI】文心一言的使用分享
在数字化时代,人工智能(AI)技术的飞速发展正在改变我们的生活。文心一言,作为这一浪潮中的佼佼者,以其卓越的自然语言处理能力和广泛的应用场景,给我带来了前所未有的使用体验。在这篇分享中,我…...
)
Java学习-MyBatis学习(四)
代码下载 解决字段名与属性名不一致 ①使用别名emp_name empName解决字段名和属性名不一致 <select id"getAllEmpOld" resultType"Emp"><!--①使用别名emp_name empName解决字段名和属性名不一致-->select eid,emp_name empName,age,sex,em…...
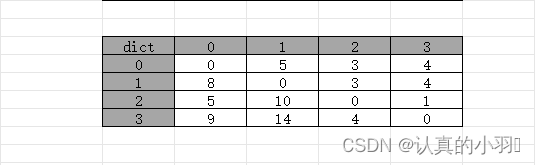
多源最短路径算法 -- 弗洛伊德(Floyd)算法
1. 简介 Floyd算法,全名为Floyd-Warshall算法,亦称弗洛伊德算法或佛洛依德算法,是一种用于寻找给定加权图中所有顶点对之间的最短路径的算法。这种算法以1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特弗洛伊德的名字命名。 2. 核心思…...

同三维T80005EH4 H.265 4路高清HDMI编码器
同三维T80005EH4 H.265 4路高清HDMI编码器 4路HDMI输入2路3.5音频输入,第1路和第2路HDMI可支持4K30,其它支持高清1080P60 产品简介: 同三维T80005EH4 4路HDMI高清H.265编码器采用最新高效H.265高清数字视频压缩技术,具备稳定…...

焦化行业排放平台简介
在当今社会,环保事业日益受到人们的关注。焦化行业作为重要的工业领域之一,其排放问题一直是环保工作的重点。为了有效控制焦化行业的排放,实施焦化行业排放平台成为了必不可少的措施。朗观视觉小编将详细探讨焦化行业排放平台的实施范围&…...
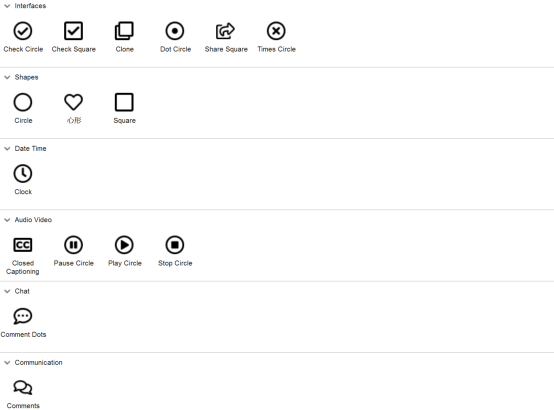
『原型资源』Axure自带图标库不够用,第三方经典图标库来袭
今天小编为大家带来第三方经典图标库,己确认内容可用现推荐给大家。直接上手就可不用自己画哈~ 获取原型文档请与班主任联系! 先睹为快,合适再拿走不谢: 图标太多,截取部分给大家参考o(* ̄︶ ̄*…...

修改版的VectorDBBench更好用
原版本VectorDBBench的几个问题 在这里就不介绍VectorDBBench是干什么的了,上官网即可。 1.并发数设置的太少 2.测试时长30秒太长 3.连接milvus无用户和密码框,这个是最大的问题 4.修改了一下其它参数 由于很多网友发私信问一些milvus的相关技术问…...

六西格玛培训都培训哪些内容 ?
天行健六西格玛培训的内容通常涵盖多个方面,旨在帮助学员全面理解和应用六西格玛管理方法。以下是详细的培训内容概述: 一、六西格玛基础知识 引入六西格玛的概念、原理和历史,包括DMAIC(定义、测量、分析、改进、控制࿰…...

K8S环境部署Prometheus
K8S环境部署Prometheus 记录在K8S 1.18版本环境下部署Prometheus 0.5版本。 1. 下载kube-prometheus仓库 git clone https://github.com/coreos/kube-prometheus.git cd kube-prometheus笔者安装的K8S版本是1.18 ,prometheus选择配套的分支release-0.5࿱…...

在linux系统上挂载新硬盘
服务器的硬盘空间不够了,自己重新安装了一个硬盘,需要挂载,因为只是用来存放数据,所以不需要分区,直接挂载就可以 #查看当前所有硬盘 sudo fdisk -l #用于显示文件系统的磁盘空间使用情况 df -h发现一个/dev/nvme0n1 …...

1004.最大连续1的个数
给定一个二进制数组 nums 和一个整数 k,如果可以翻转最多 k 个 0 ,则返回 数组中连续 1 的最大个数 。 示例 1: 输入:nums [1,1,1,0,0,0,1,1,1,1,0], K 2 输出:6 解释:[1,1,1,0,0,1,1,1,1,1,1] 粗体数字…...

【机器学习300问】116、什么是序列模型?序列模型能干什么?
一、序列模型是什么? 序列模型是机器学习领域中专门设计来处理具有时间顺序或序列结构数据的模型。这类模型能够理解和学习数据中的顺序依赖关系,因此非常适合诸如自然语言处理、语音识别、音乐生成、时间序列预测等任务。 看了上面的定义,似…...

kafka 快速上手
下载 Apache Kafka 演示window 安装 编写启动脚本,脚本的路径根据自己实际的来 启动说明 先启动zookeeper后启动kafka,关闭是先关kafka,然后关闭zookeeper 巧记: 铲屎官(zookeeper)总是第一个到,最后一个走 启动zookeeper call bi…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...
