齐普夫定律在循环神经网络中的语言模型的应用
目录
- 齐普夫定律解释
- 公式解释
- 图与公式的关系
- 代码与图的分析
- 结论
- 使用对数表达方式的原因
- 1. 线性化非线性关系
- 2. 方便数据可视化和分析
- 3. 降低数值范围
- 4. 方便参数估计
- 公式详细解释
- 结论

来自:https://zh-v2.d2l.ai/chapter_recurrent-neural-networks/language-models-and-dataset.html


齐普夫定律解释
齐普夫定律(Zipf’s Law)是一种描述自然语言中单词频率分布的经验法则,它指出在一个文本或语料库中,单词的频率与其出现的排名成反比关系。具体来说,频率最高的单词出现的次数最多,排名第二的单词出现的次数大约是最高频单词的一半,排名第三的单词出现次数是最高频单词的三分之一,依此类推。
公式解释
齐普夫定律的数学表达式可以表示为:
n i ∝ 1 i α n_i \propto \frac{1}{i^\alpha} ni∝iα1
其中, n i n_i ni 表示第 ( i ) 个单词的频率,( i ) 是该单词的排名,( \alpha ) 是一个常数。为了便于理解,这个公式可以变形为:
[ n_i = \frac{C}{i^\alpha} ]
其中 ( C ) 是一个归一化常数。
在图8.3.7和8.3.8中,这个公式被进一步转化为对数形式,以便在对数坐标系中表现出线性关系:
[ \log n_i = -\alpha \log i + c ]
这里,( \log n_i ) 是单词频率的对数,( \log i ) 是单词排名的对数,( \alpha ) 是斜率,( c ) 是截距。
图与公式的关系
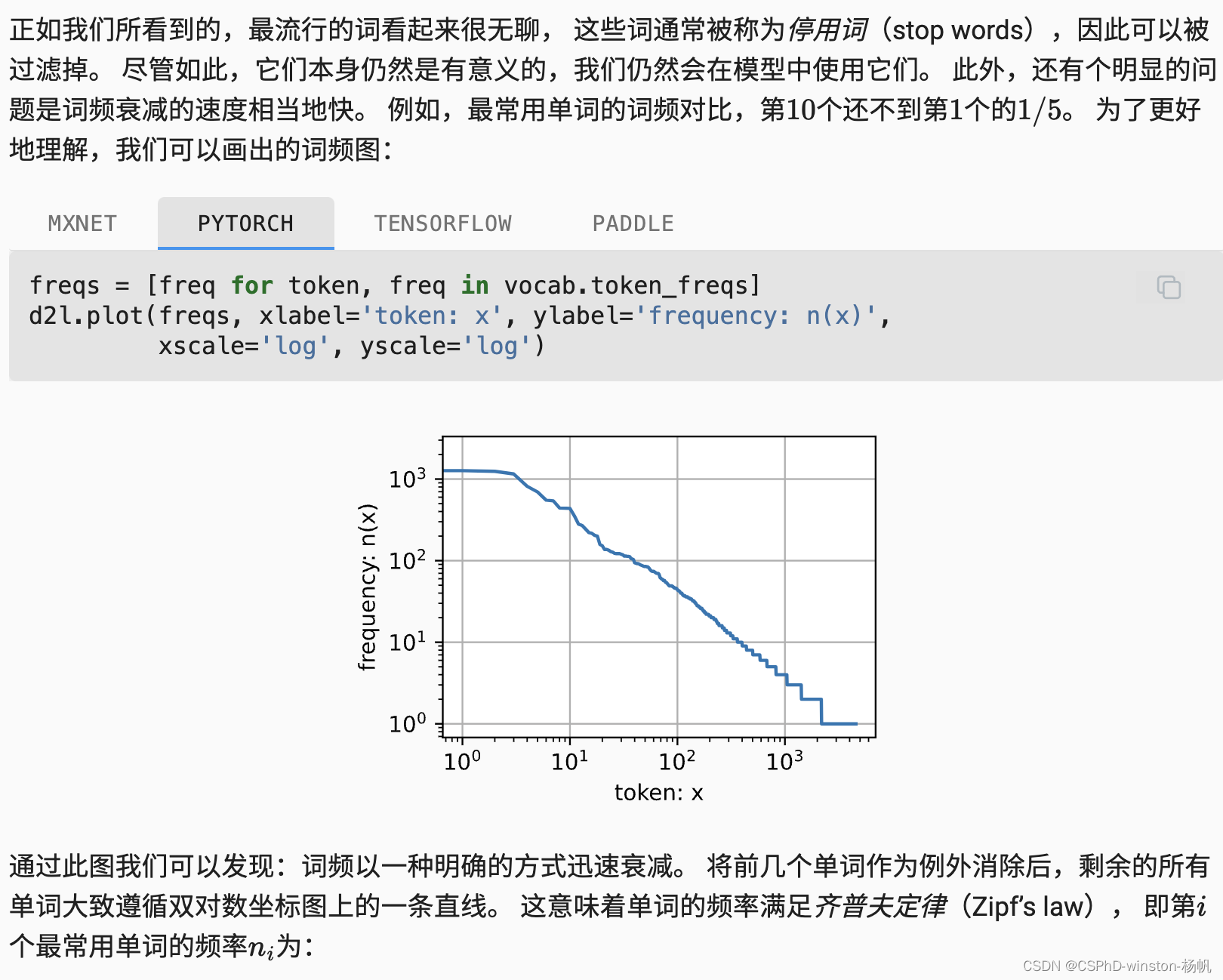
在图中绘制了词频与排名的对数图。通过对图像进行对数变换,可以观察到频率与排名之间的关系是否遵循齐普夫定律。如果单词频率与排名在对数坐标系中呈现一条直线,这意味着词频与排名确实遵循齐普夫定律,即:
[ \log n_i = -\alpha \log i + c ]
从图中我们可以看到,词频分布在对数坐标系中近似为一条直线,这验证了齐普夫定律的正确性。
代码与图的分析
从代码和图中,我们可以看到以下几个步骤:
- 统计词频:读取文本数据并进行分词,统计每个单词的出现频率。
- 排序:根据单词的出现频率对单词进行排序,得到每个单词的排名。
- 绘制图形:在对数坐标系中绘制单词的频率和排名的关系图。
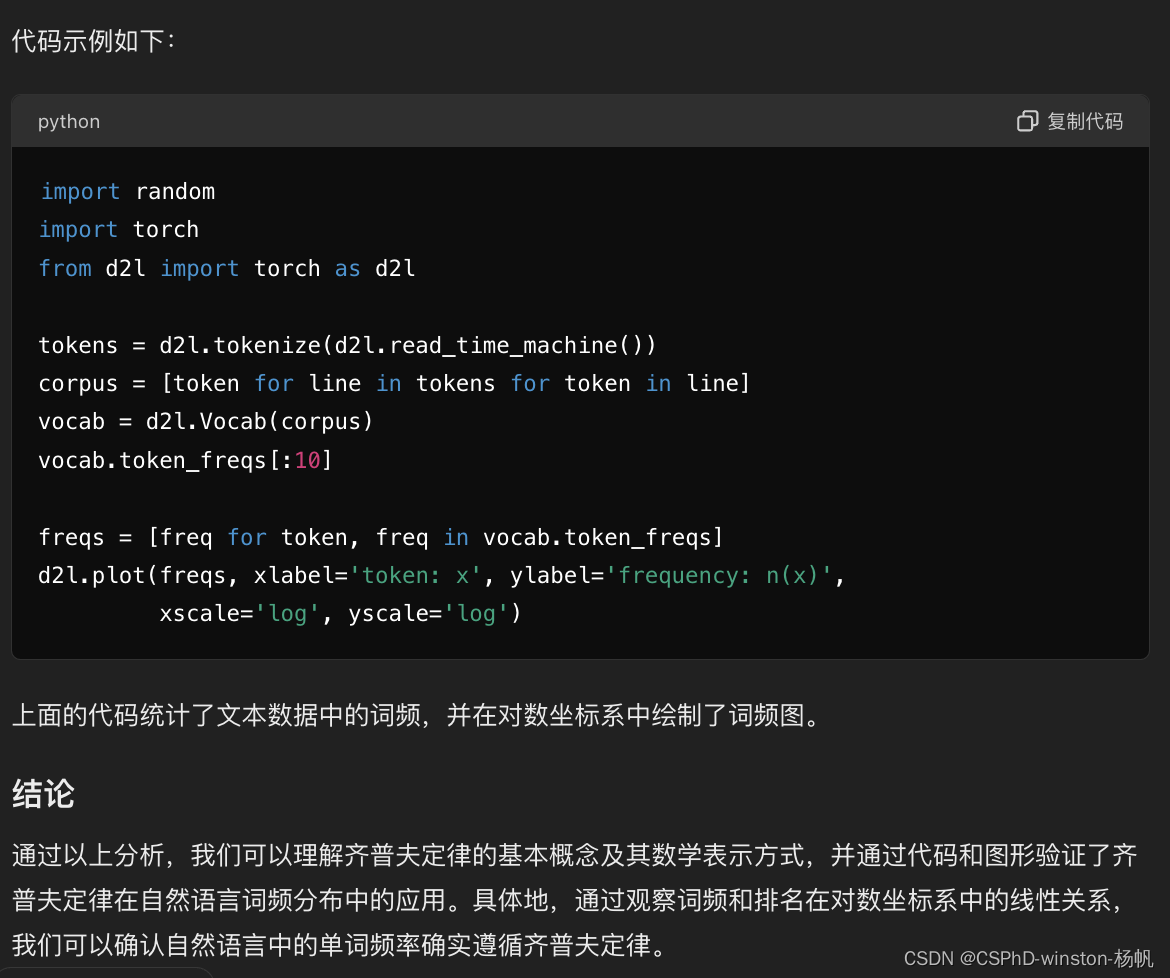
代码示例如下:
import random
import torch
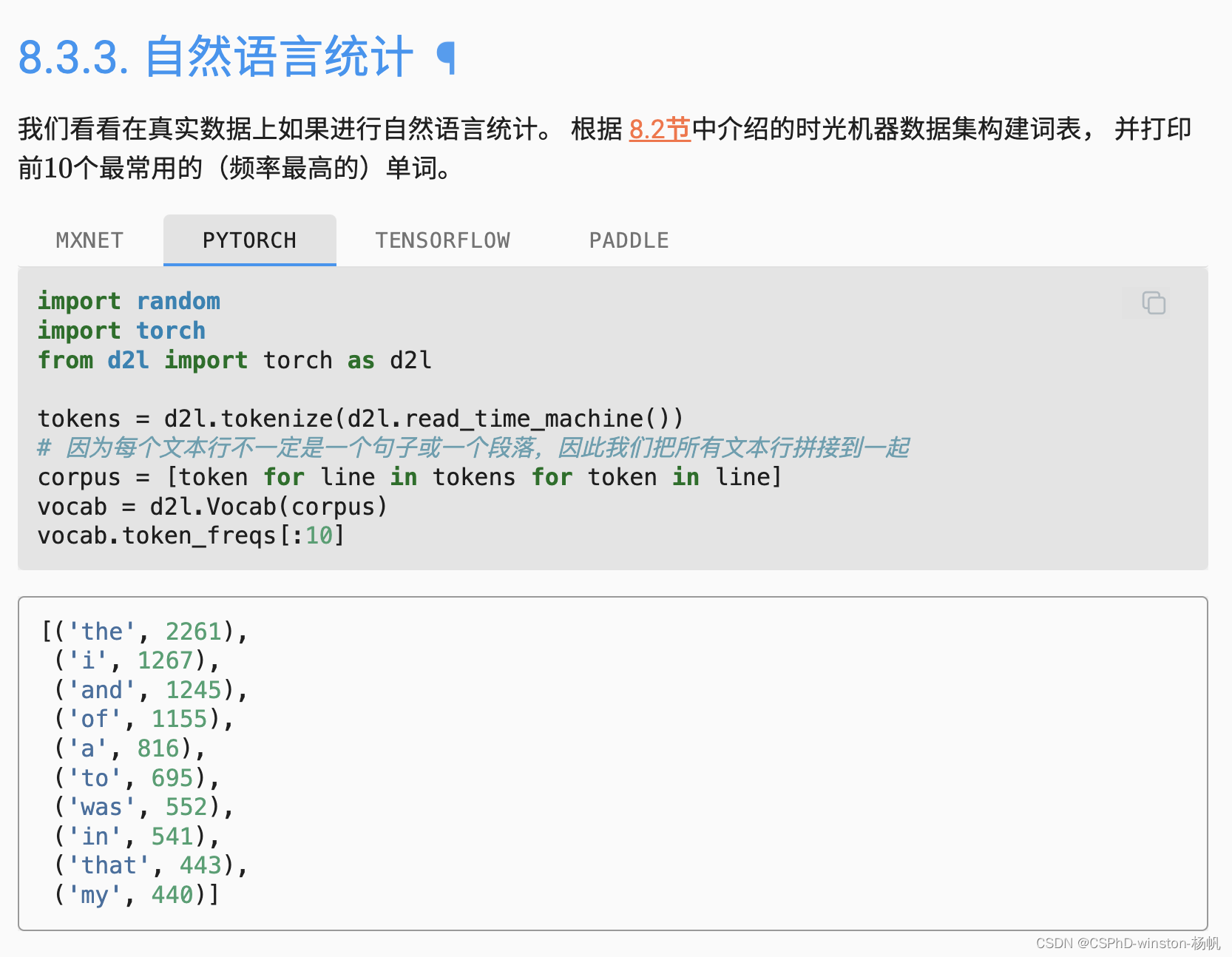
from d2l import torch as d2ltokens = d2l.tokenize(d2l.read_time_machine())
corpus = [token for line in tokens for token in line]
vocab = d2l.Vocab(corpus)
vocab.token_freqs[:10]freqs = [freq for token, freq in vocab.token_freqs]
d2l.plot(freqs, xlabel='token: x', ylabel='frequency: n(x)',xscale='log', yscale='log')
上面的代码统计了文本数据中的词频,并在对数坐标系中绘制了词频图。
结论
通过以上分析,我们可以理解齐普夫定律的基本概念及其数学表示方式,并通过代码和图形验证了齐普夫定律在自然语言词频分布中的应用。具体地,通过观察词频和排名在对数坐标系中的线性关系,我们可以确认自然语言中的单词频率确实遵循齐普夫定律。


使用对数表达方式的原因
使用对数表达方式([ \log n_i = -\alpha \log i + c ])的原因主要有以下几点:
1. 线性化非线性关系
齐普夫定律本身是一个非线性关系:
[ n_i \propto \frac{1}{i^\alpha} ]
通过取对数,两边都取对数后变为线性关系:
[ \log n_i = -\alpha \log i + c ]
这使得我们可以用直线来描述这个关系,而直线在统计学和数据分析中更容易处理和理解。
2. 方便数据可视化和分析
对数坐标系能够更直观地展示数据的幂律分布特性。在对数坐标系中,幂律分布的数据点会呈现为一条直线,这使得我们可以更容易地识别和验证数据是否符合齐普夫定律。
在图中,横轴(单词排名)和纵轴(单词频率)都取对数,如果数据点近似排列成一条直线,就说明词频分布符合齐普夫定律。这种图形化表示使得观察和分析数据的分布规律变得直观和简单。
3. 降低数值范围
自然语言中的单词频率差异很大,频率最高的单词和频率最低的单词可能相差几个数量级。直接使用原始数据进行分析和可视化会遇到数值范围过大的问题,导致图形难以阅读和解释。而通过取对数,可以压缩数据的范围,使得不同频率的单词在图中更紧凑地展示,便于比较和分析。
4. 方便参数估计
在对数空间中,线性回归可以用来估计幂律分布中的参数。通过线性回归,我们可以得到斜率 ( -\alpha ) 和截距 ( c ),进而估计出原始幂律分布的参数。这在统计建模和参数估计中非常实用。
公式详细解释
原始齐普夫定律公式:
[ n_i \propto \frac{1}{i^\alpha} ]
取对数后变为:
[ \log n_i = \log \left( \frac{C}{i^\alpha} \right) ]
其中 ( C ) 是归一化常数,进一步分解:
[ \log n_i = \log C - \alpha \log i ]
将 ( \log C ) 记作 ( c )(因为 ( C ) 是常数,所以 ( \log C ) 也是常数),最终得到:
[ \log n_i = -\alpha \log i + c ]
结论
通过使用对数表达方式,我们将非线性的幂律关系转化为线性关系,使得数据可视化、分析和参数估计变得更加直观和方便。这种方法不仅简化了分析过程,也增强了结果的解释力和可视化效果。
相关文章:

齐普夫定律在循环神经网络中的语言模型的应用
目录 齐普夫定律解释公式解释图与公式的关系代码与图的分析结论 使用对数表达方式的原因1. 线性化非线性关系2. 方便数据可视化和分析3. 降低数值范围4. 方便参数估计公式详细解释结论 来自:https://zh-v2.d2l.ai/chapter_recurrent-neural-networks/language-model…...

如何在Android Studio上发布Flutter应用
发布Flutter应用到Android平台是一个多步骤的过程,涉及配置应用、生成签名密钥、配置Gradle文件、构建发布版本APK等步骤。本文将详细介绍这些步骤,帮助你顺利发布Flutter应用。 1. 准备你的应用 在发布之前,确保你的应用在开发环境中运行良…...

C++ 字符串处理4-根据指定的分隔符将字符串分割为多个子串根据指定的分隔符将多个子串连接成一个字符串
1. 关键词 C 字符串处理 分割字符串 连接字符串 跨平台 2. strutil.h #pragma once#include <string> #include <vector>namespace cutl {/*** brief The type of vector strings used in this library.**/using strvec std::vector<std::string>;/*** b…...
微信小程序请求request封装
公共基础路径封装 // config.js module.exports {// 测试BASE_URL: https://cloud.chejj.cn,// 正式// BASE_URL: https://cloud.mycjj.com };请求封装 // request.js import config from ../config/baseUrl// 请求未返回时的loading const showLoading () > wx.showLoadi…...

Web前端不挂科:深入探索与实战指南
Web前端不挂科:深入探索与实战指南 在数字化时代的浪潮中,Web前端开发已成为一项炙手可热的技能。然而,对于许多初学者来说,如何避免在Web前端课程中挂科却成为了一道难题。本文将从四个方面、五个方面、六个方面和七个方面&…...
Golang | Leetcode Golang题解之第149题直线上最多的点数
题目: 题解: func maxPoints(points [][]int) (ans int) {n : len(points)if n < 2 {return n}for i, p : range points {if ans > n-i || ans > n/2 {break}cnt : map[int]int{}for _, q : range points[i1:] {x, y : p[0]-q[0], p[1]-q[1]if…...

京准电钟 NTP时间同步服务器助力水库水坝水利自动化建设
京准电钟 NTP时间同步服务器助力水库水坝水利自动化建设 京准电钟 NTP时间同步服务器助力水库水坝水利自动化建设 水库大坝监测系统主要包括渗流监测系统、流量监测系统、雨量监测系统、沉降监测系统组成。每一个监测系统由监测仪器及自动化数据采集装置(内置通信装…...

程序员应该具备什么职业素养?
程序员应该有什么职业素养? 作为一个程序员,拥有以下职业素养是非常重要的: 扎实的技术功底:作为程序员,首先要具备扎实的技术基础,包括编程语言、算法、数据结构等方面的知识,能够熟练地解决问…...
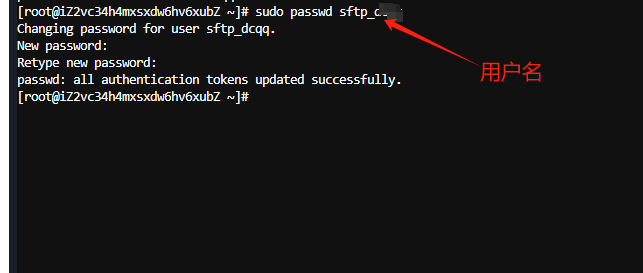
linux 安装sftp及使用sftp上传和下载
一、centos7 安装sftp 1.安装 OpenSSH 服务: sudo yum install openssh-server2.启动 SSH 服务,并设置为开机启动: sudo systemctl start sshd sudo systemctl enable sshd3.创建一个新用户,用于SFTP连接(替换your_…...

AI虚拟试穿技术:开启高保真、多场景、多样化服装组合的试穿应用
随着电子商务的快速发展,消费者对于在线购物体验的要求越来越高。特别是在服装领域,消费者渴望能够在购买前直观地了解服装的试穿效果。传统的虚拟试穿技术虽然已有一定的发展,但在不同场景下的高保真度和鲁棒性方面仍面临挑战。为此,我们研发了一种全新的AI虚拟试穿技术,…...
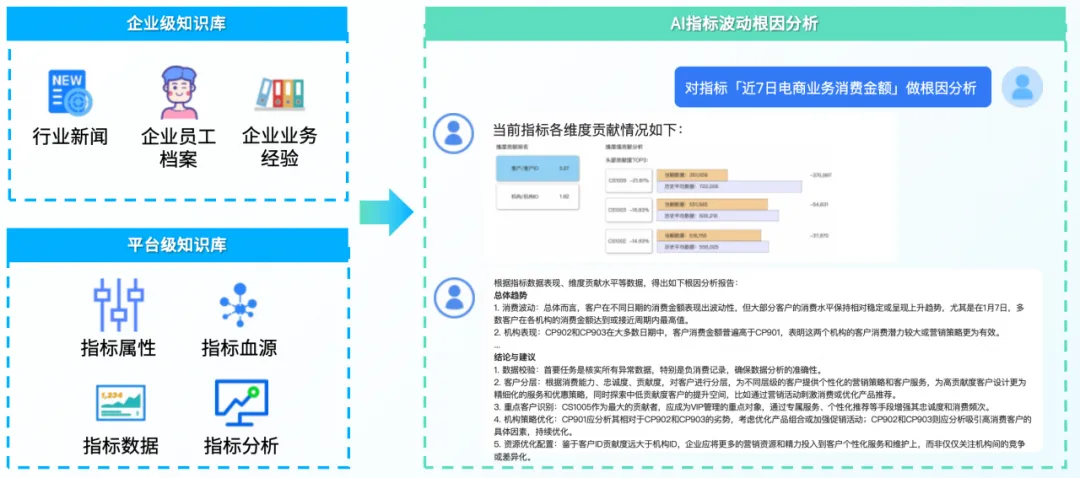
数栈xAI:轻量化、专业化、模块化,四大功能革新 SQL 开发体验
在这个数据如潮的时代,SQL 已远远超越了简单的查询语言范畴,它已成为数据分析和决策制定的基石,成为撬动企业智慧决策的关键杠杆。SQL 的编写和执行效率直接关系到数据处理的速度和分析结果的深度,对企业洞察市场动态、优化业务流…...

oppo手机精简包名列表
oppo广告机,coloros为13.0,测试机为oppo a1x 5g。 手机第一次开机后就全屏广告,被恶心了好几个月。现使用universal Android debolater进行卸载测试,其中: 不可卸载的: 开机广告:com.coloros.…...
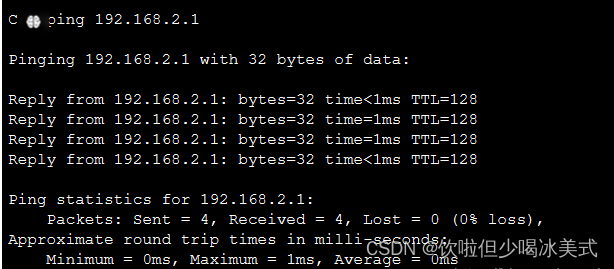
Cisco Packet Tracer实验(二)
二、用交换机构建 LAN 构建物件如下: 四个PC 两个交换机 一个Multi Switch多功能拓展控制器 连线必须是这个直线!!!不是虚线 最后实现效果如下: 全部的线是绿的,就表示是通的。 尝试一下,看PC…...

Julia 数学函数
Julia 数学函数 Julia 是一种高性能的动态编程语言,特别适合于数值计算和科学计算。在数学领域,Julia 提供了丰富的内置函数,这些函数涵盖了从基本运算到高级数学运算的各个方面。本文将详细介绍 Julia 中的数学函数,并提供一些示例,帮助读者更好地理解和使用这些函数。 …...
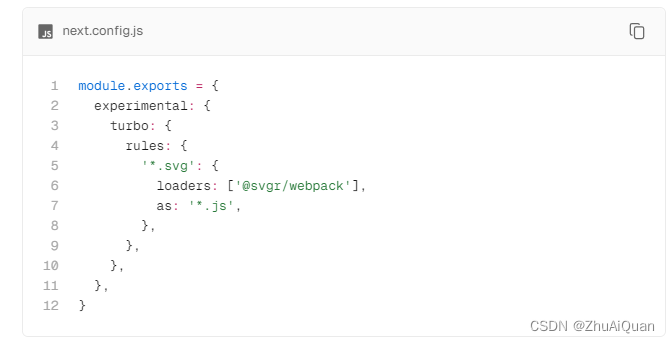
[next.js] svgr/webpack
nextjs如何配置svg文件,使其像react组件一样导入? 当前next.js 开发环境我使用了--turbo 来开启turbopack加速文件构建,所以之前的一些webpack loader之类的无法正常工作。通过搜索发现一般都是使用svgr/webpack来处理svg,打开svgr官网发现…...
vue页面和 iframe多页面无刷新方案和并行存在解决方案
面临问题 : back的后台以jsp嵌套iframe为主, 所以在前端框架要把iframe无刷新嵌套和vue页面进行并行使用,vue的keep-alive只能对虚拟dom树 vtree 进行缓存无法缓存iframe,所以要对iframe进行处理 tab标签的切换效果具体参考若依框架的tab切换,可以去若依看源码,若依源码没有实…...
Leetcode498. 对角线遍历
Every day a Leetcode 题目来源:498. 对角线遍历 解法1:模拟 根据题目要求,矩阵按照对角线进行遍历。设矩阵的行数为 m,矩阵的列数为 n,我们仔细观察对角线遍历的规律可以得到如下信息: 一共有 mn−1 条…...

flume配置----a1.sources.r1.positionFile=xxxx.json
positionFile 的作用和用途 记录读取位置: positionFile 记录了 Flume 读取文件的当前位置(偏移量),确保在 Flume 重启或崩溃后,能够从上次读取的位置继续读取文件,而不是重新开始读取。这在处理大文件或长…...

Controller 自动化日志输出
Starter库 1.定义注解 Target(ElementType.METHOD) Retention(RetentionPolicy.RUNTIME) Documented public interface TraceLog {/*** 日志类型** return*/String type() default ""; }2.定义捕获日志接口方法 public interface ITraceLogProcess {void afterThr…...
?)
css3中有哪些新属性(特性)?
在 CSS3 中引入了许多新的属性和特性,以下是其中一些主要的: Flexbox(弹性盒子布局):通过 display: flex 及其相关属性,实现灵活的布局方式,使得元素在容器中可以自动调整大小和位置。 Grid&am…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...
