算法刷题【二分法】
题目:


- 注意题目中说明了数据时非递减的,那么这样就存在二分性,能够实现logn的复杂度。
- 二分法每次只能取寻找特定的某一个值,所以我们要分别求左端点和有端点。
分析第一组用例得到结果如下:

成功找到左端点8
由此可知,用二分法去寻找左端端点的时候:
-
若
num[mid]<target,那么此时mid的左边包括自身的值都小于target,所以直接执行赋值操作left = mid + 1即可。 -
当
num[mid]= =target的时候,由于可能此时的mid已经是左端端点了。但是只是可能是左端点了,也有可能不是左端点,所以相等的情况就要和大于的情况合并起来操作,执行right = mid操作。 -
当
num[mid]>target的时候,mid的右边包括自身都比target的值要大,执行right = mid具有合理性,不能执行right = mid -1因为此时和等于合并起来了,判断条件变成是num[mid] <= target在等于的情况下,可能成为左端的端点。
图示*😗

上述就是找最左边的端点的基本思路了,但是我们还有一些细节需要处理: -
对于每次mid位置的取发:
1:mid = left + (right-left)/2
2:mid = left + (right-left +1)/2
有以上两种取法,前后者在奇数的情况下相同,但是在偶数的情况下就会有所不同。
偶数的情况下,1会取到中间两个数的片左边的那一个,2会取到中间两个数的偏右边那一个。
对于取左边端点来说:
到最终可能会有这么一种的情况:

所以在用二分法寻找左侧端点的时候,应该要使用mid的第一种取法(mid = left + (right-left)/2 )。
相关文章:

算法刷题【二分法】
题目: 注意题目中说明了数据时非递减的,那么这样就存在二分性,能够实现logn的复杂度。二分法每次只能取寻找特定的某一个值,所以我们要分别求左端点和有端点。 分析第一组用例得到结果如下: 成功找到左端点8 由此可知࿰…...
.NET MAUI Sqlite程序应用-数据库配置(一)
项目名称:Ownership(权籍信息采集) 一、安装 NuGet 包 安装 sqlite-net-pcl 安装 SQLitePCLRawEx.bundle_green 二、创建多个表及相关字段 Models\OwnershipItem.cs using SQLite;namespace Ownership.Models {public class fa_rural_base//基础数据…...
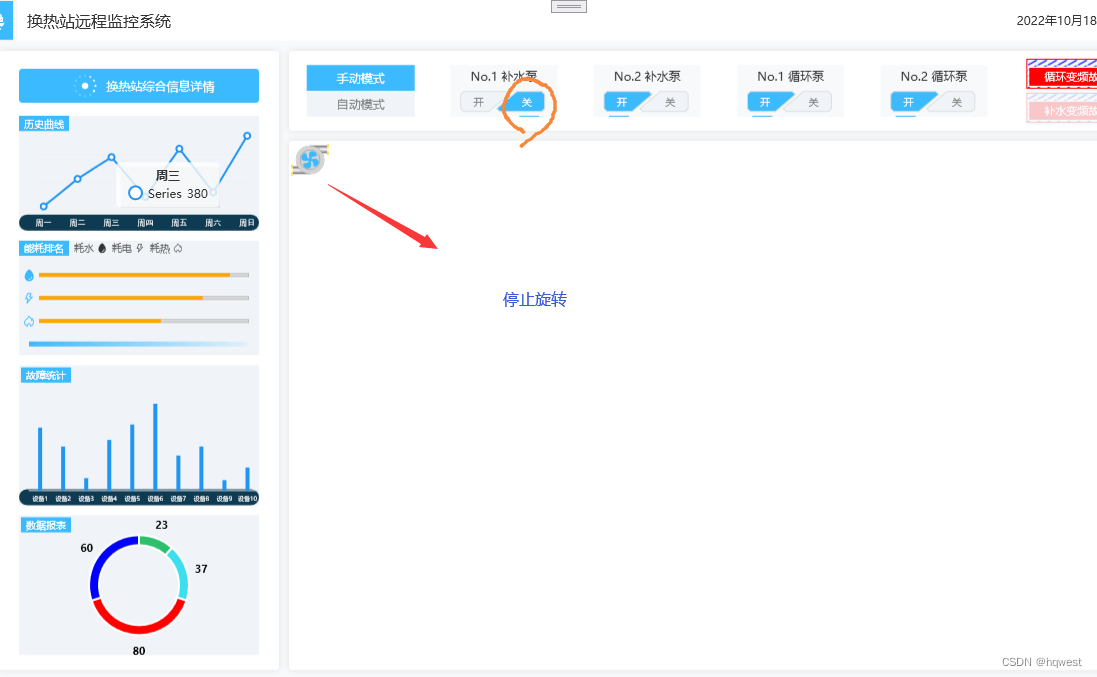
基于WPF技术的换热站智能监控系统09--封装水泵对象
1、添加用户控件 2、编写水泵UI 控件中用到了Viewbox控件,Viewbox控件是WPF中一个简单的缩放工具,它可以帮助你放大或缩小单个元素,同时保持其宽高比。通过样式和属性设置,你可以创建出既美观又功能丰富的用户界面。在实际开发中…...

GLM+vLLM 部署调用
GLMvLLM 部署调用 vLLM 简介 vLLM 框架是一个高效的大型语言模型(LLM)推理和部署服务系统,具备以下特性: 高效的内存管理:通过 PagedAttention 算法,vLLM 实现了对 KV 缓存的高效管理,减少了…...

leetcode 122 买卖股票的最佳时机||(动态规划解法)
题目分析 题目描述的已经十分清楚了,不做过多阐述 算法原理 状态表示 我们假设第i天的最大利润是dp[i] 我们来画一下状态机 有两个状态,买入后和卖出后,我们就可以使用两个dp表来解决问题 f[i]表示当天买入后的最大利润 g[i]表示当天卖出…...

C++设计模式---组合模式
1、介绍 组合模式(Composite)是一种结构型设计模式,也被称为部分-整体模式。它将复杂对象视为由多个简单对象(称为“组件”)组成的树形结构,这些组件能够共享相同的行为。每个组件都可能包含一个或多个子组…...
C/C++版本)
工厂方法模式(大话设计模式)C/C++版本
工厂方法模式 C 参考:https://www.cnblogs.com/Galesaur-wcy/p/15926711.html #include <iostream> #include <memory> using namespace std;// 运算类 class Operation { private:double _NumA;double _NumB;public:void SetNumA(){cout << &…...

[NCTF 2018]flask真香
打开题目后没有提示框,尝试扫描后也没有什么结果,猜想是ssti。所以尝试寻找ssti的注入点并判断模版。 模版判断方式: 在url地址中输入{7*7} 后发现不能识别执行。 尝试{{7*7}} ,执行成功,继续往下走注入{{7*7}},如果执…...

性能测试3【搬代码】
1.Linux服务器性能分析命令及详解 2.GarafanainfluxDB监控jmeter数据 3.GarafanaPrometheus监控服务器和数据库性能 4.性能瓶颈分析以及性能调优方案详解 一、无界面压测时, top load average:平均负载 htop 二、Garafana监控平台 传统项目:centosphpm…...

<tesseract><opencv><Python>基于python和opencv,使用ocr识别图片中的文本并进行替换
前言 本文是在python中,利用opencv处理图片,利用tesseractOCR来识别图片中的文本并进行替换的一种实现方法。 环境配置 系统:windows 平台:visual studio code 语言:python 库:pyqt5、opencv、tesseractOCR 代码介绍 本文程序功能实现,主要依赖于tesseractOCR这个库,…...

海南云亿商务咨询有限公司解锁抖音电商新纪元
在当今数字化浪潮中,抖音电商以其独特的魅力和强大的用户基础,迅速成为企业营销的新宠。海南云亿商务咨询有限公司,作为专注于抖音电商服务的领先企业,凭借专业的团队和丰富的经验,为众多企业提供了高效、精准的电商服…...
)
arm64架构 统信UOS搭建PXE无盘启动Linux系统(麒麟桌面为例)
arm64架构 统信UOS搭建PXE无盘启动Linux系统(麒麟桌面为例) 搞了好久搞得头疼哎 1、准备服务器UOS服务器 准备服务IP 这里是192.168.1.100 1.1、安装程序 yum install -y dhcp tftp tftp-server xinetd nfs-utils rpcbind 2、修改配置 2.1、修改dhcpd.c…...
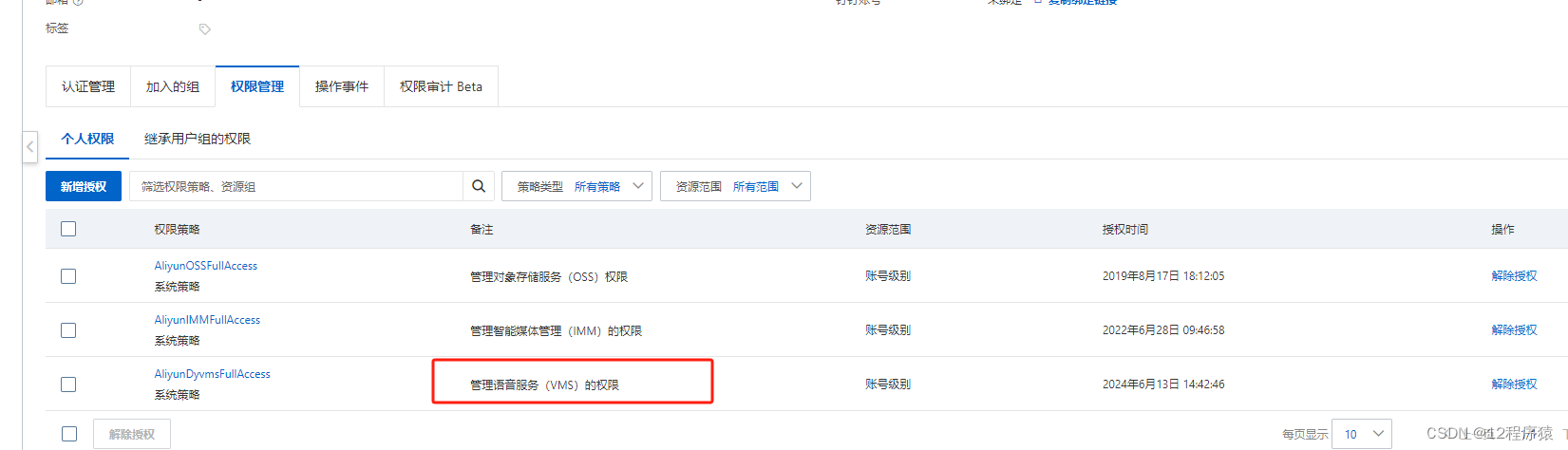
SpringBoot 实现 阿里云语音通知(SingleCallByTts)
目录 一、准备工作1.开通 阿里云语音服务2.申请企业资质3.创建语音通知模板,审核通过4.调用API接口---SingleCallByTts5.调试API接口---SingleCallByTts 二、代码实现1.导入依赖 com.aliyun:aliyun-java-sdk-dyvmsapi:3.0.22.创建工具类,用于发送语音通知…...
IDEA 连接GitHub仓库并上传项目(同时解决SSH问题)
目录 1 确认自己电脑上已经安装好Git 2 添加GitHub账号 2.1 Setting -> 搜索GitHub-> ‘’ -> Log In with Token 2.2 点击Generate 去GitHub生成Token 2.3 勾选SSH后其他不变直接生成token 2.4 然后复制token添加登录账号即可 3 点击导航栏中VCS -> Create…...

vue/react/js 常用的原生获取当前页面的url网址的相关方法
目录 第一章 场景 第二章 总结 第一章 场景 最近实现需求时遇到这么一种情况: 本地url —— 线上url —— 需求:需要将token清除掉 注意事项:token不是#/后面的参数,说明并不是我们前端返回的,vue路由的方法使用不…...

java-final 关键字
## Java中的final关键字 ### 1. final关键字的基本概念 final是Java中一个非常重要的关键字,用于声明常量、阻止继承和重写,确保类、方法和变量的不可变性。具体来说,final关键字可以用来修饰类、方法和变量(包括成员变量和局部…...
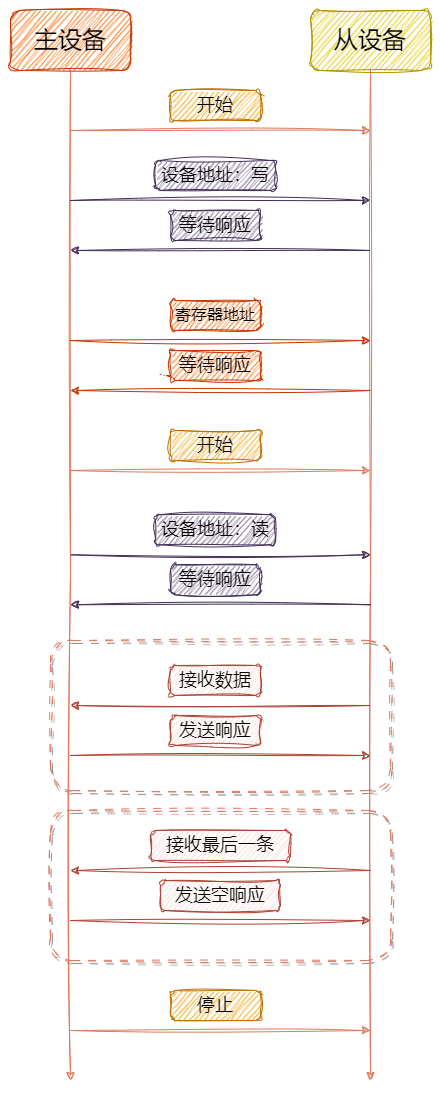
ARM32开发--IIC软实现
知不足而奋进 望远山而前行 目录 文章目录 前言 开发流程 GD32F4软件I2C初始化 GD32F4软件I2C引脚功能 写操作 读操作 总结 前言 在嵌入式系统开发中,软件实现的I2C通信协议扮演着至关重要的角色。本文将深入探讨如何在GD32F4系列微控制器上实现软件I2C功能…...
中实现拓扑排序与最短路径和最长路径算法)
在有向无环图(DAG)中实现拓扑排序与最短路径和最长路径算法
有向无环图(DAG)是一类非常重要的图结构,广泛应用于任务调度、数据依赖分析等领域。本文将介绍如何在DAG中实现拓扑排序、单源最短路径和单源最长路径算法,并提供完整的Java代码示例。 图结构定义 首先,我们定义一个…...

SQLServer按照年龄段进行分组查询数据
1.按照年龄段对数据进行分组, 将人群分为:青年,中年,老年三种类型,人群类型加上其他分组字段如:性别,进行多条件分组,统计各个年龄段多少人 Select case sex when 1 then ‘男’ when 2 then …...

开放式耳机哪个品牌质量比较好?2024高性价比机型推荐!
随着音乐技术的不断发展,开放式耳机已成为音乐发烧友们的另外一种选择。从最初的简单音质,到如今的高清解析,开放式耳机不断进化升级。音质纯净,佩戴舒适,无论是街头漫步还是家中放松时候,都能带给你身临其…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
