TOP150-LC88
/*给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n*/
public class lc88 {public void merge(int[] nums1, int m, int[] nums2, int n) {int i = m - 1;int j = n - 1;int p = nums1.length - 1;while (i >= 0 && j >= 0) {if (nums1[i] > nums2[j]) {nums1[p] = nums1[i];i--;} else {nums1[p] = nums2[j];j--;}p--;}while (j >= 0) {nums1[p] = nums2[j];j--;}}
}
相关文章:

TOP150-LC88
/*给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。注意:最终,合并后数组不…...
使用Python和TCN进行时间序列预测:一个完整的实战示例
使用Python和TCN进行时间序列预测:一个完整的实战示例 时间卷积网络(TCN)已被证明在处理序列数据方面表现出色,尤其是在需要捕获长期依赖关系的任务中。在本文中,我们将通过一个简单的例子,展示如何使用Py…...
如何用R语言ggplot2画高水平期刊散点图
文章目录 前言一、数据集二、ggplot2画图1、全部代码2、细节拆分1)导包2)创建图形对象3)主题设置4)轴设置5)图例设置6)散点颜色7)保存图片 前言 一、数据集 数据下载链接见文章顶部 处理前的数据…...

Python基于 Jupyter Notebook 的图形可视化工具库之ipysigma使用详解
概要 在数据科学和网络分析中,图(Graph)结构是一种常用的数据结构,用于表示实体及其关系。为了方便图数据的可视化和交互操作,ipysigma 提供了一个基于 Jupyter Notebook 的图形可视化工具。通过 ipysigma,用户可以在 Jupyter Notebook 中创建、编辑和展示图结构,方便进…...

四叉树和KD树
1. 简介 四叉树和KD树都是用于空间数据索引和检索的树状数据结构。它们通过将空间递归地划分为更小的区域,并存储每个区域内的点,来实现快速搜索和范围查询。 2. 四叉树 2.1 定义 四叉树是一种树状数据结构,它将二维空间递归地划分为四个…...

C语言中结构体使用.与->访问成员变量的区别
文章目录 前言点运算符(.)箭头运算符(->)总结 前言 在C语言中,. 和 -> 都是用来访问结构体成员的运算符,但它们的使用场景和含义有所不同。 提示:以下是本篇文章正文内容,下面…...

计算机二级Access选择题考点
在Access中,若要使用一个字段保存多个图像、图表、文档等文件,应该设置的数据类型是附件。在“销售表"中有字段:单价、数量、折扣和金额。其中,金额单价x数量x折扣,在建表时应将字段"金额"的数据类型定义为计算。若…...

人工智能历史与现状
1 人工智能历史与现状 1.1 人工智能的概念和起源 1.1.1 人工智能的概念 人工智能 (Artificial Intelligence ,AI)是一门研究如何使计算机 能够模拟人类智能行为的科学和技术,目标在于开发能够感知、理解、 学习、推理、决策和解决问题的智能机器。人工智能的概念主要包含 以…...

【git使用一】windows下git下载、安装和卸载
目录 (1)下载安装包 (2)安装git (3)安装验证 (4)卸载git (1)下载安装包 官网下载地址:Git 国内镜像下载地址:CNPM Binaries Mir…...

JVM 类加载器的工作原理
JVM 类加载器的工作原理 类加载器(ClassLoader)是一个用于加载类文件的子系统,负责将字节码文件(.class 文件)加载到 JVM 中。Java 类加载器允许 Java 应用程序在运行时动态地加载、链接和初始化类。 2. 类加载器的工…...

ARM Cortex-M4 CPU指令大全:作用、原理与实例
引言 在计算机系统中,CPU(中央处理器)是执行各种指令的核心部件。ARM Cortex-M4是广泛应用于嵌入式系统中的一款处理器,其指令集架构(ISA)基于ARMv7-M。本文将介绍ARM Cortex-M4处理器中的常见指令&#x…...

Mysql学习(九)——存储引擎
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 七、存储引擎7.1 MySQL体系结构7.2 存储引擎简介7.3 存储引擎特点7.4 存储引擎选择7.5 总结 七、存储引擎 7.1 MySQL体系结构 连接层:最上层是一些客户…...
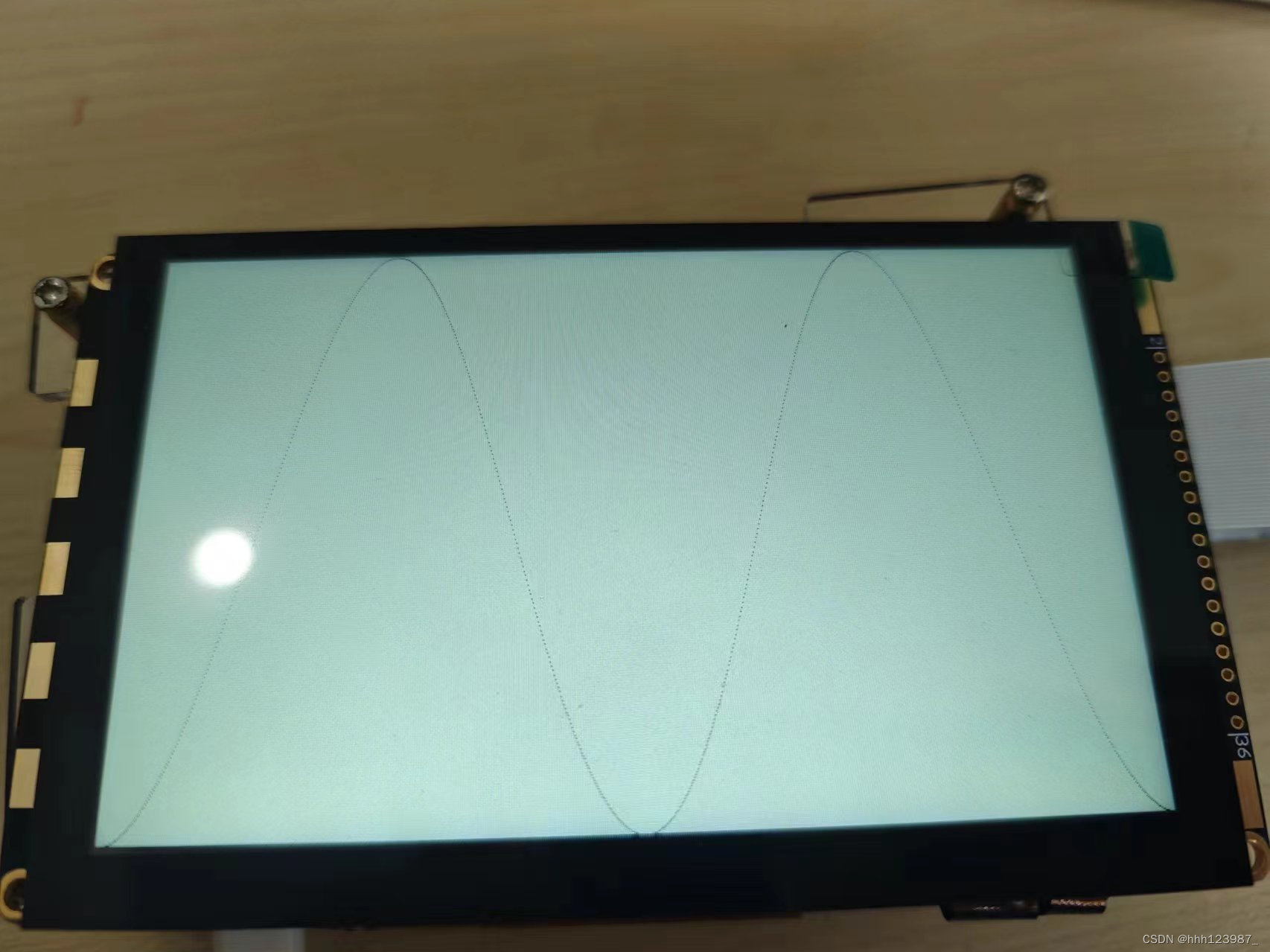
TFT屏幕波形显示
REVIEW 关于TFT显示屏,之前已经做过彩条显示: TFT显示屏驱动_tft驱动-CSDN博客 关于ROM IP核,以及coe文件生成: FPGA寄存器 Vivado IP核_fpga寄存器资源-CSDN博客 1. TFT屏幕ROM显示正弦波 ①生成coe文件 %% sin-cos wave dat…...
服务器无法远程桌面连接不上的问题排查与解决方案
一、问题概述 当尝试使用远程桌面协议(RDP)连接至服务器时,如果连接失败,这通常意味着存在一些配置问题、网络问题或服务器本身的问题。此类问题对于管理员而言,需要系统地进行排查和解决。 二、排查步骤 1. 检查网…...

JAVA面试题整理——内存溢出与内存泄露的区别与联系
内存溢出与内存泄露的区别与联系 在前面jvm学习整理的时候其实用过一个简单的例子了解过内存溢出,在jvm内存模型章节下,大家有兴趣的可以去看看:JVM初学 GC_knowwait的博客-CSDN博客 内存溢出 内存溢出(out of memory)…...

L50--- 104. 二叉树的最大深度(深搜)---Java版
1.题目描述 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。 2.思路 这个二叉树的结构如下: 根节点 1 左子节点 2 右子节点 3 左子节点 4 计算过程 从根节点 1 开始计算: 计算左子树的最大深度: 根节点 2…...

Linux 中 “ 磁盘、进程和内存 ” 的管理
在linux虚拟机中也有磁盘、进程、内存的存在。第一步了解一下磁盘 一、磁盘管理 (1.1)磁盘了解 track( 磁道 ) :就是磁盘上的同心圆,从外向里,依次排序1号,2号磁盘........等等。…...

test_pipeline
test_pipeline 是一个测试管道(test pipeline)的定义。 在计算机视觉任务中,通常需要对输入图像进行一系列的预处理操作,以便将其适配到模型的输入要求或提高模型的性能。测试管道就是用于定义这些预处理操作的一系列步骤。 在给…...

使用甲骨文云arm服务器安装宝塔时nginx无法卸载
使用甲骨文云arm服务器安装宝塔 其他环境都能安装上 唯独nginx安装完不运行 卸载了几次以后还无法卸载了. 修复 重启都不行. 差点就重建主机了. 最后靠下面的命令 就卸载掉了 然后重装就把nginx安装好了 mv /www/server/nginx/sbin/nginx /tmp/nginx_back mv /etc/in…...

C++青少年简明教程:C++的指针入门
C青少年简明教程:C的指针入门 说到指针,就不可能脱离开内存。了解C的指针对于初学者来说可能有些复杂,我们可以试着以一种简单、形象且易于理解的方式来解释: 首先,我们可以将计算机内存想象成一个巨大的有许多格子的…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...
