列表、集合、字典的相关练习
1、使用列表推导式,输出1~100的所有素数
输入下面代码
# 定义一个辅助函数用来判断是否是素数
def is_prime(num):if num <= 1:return Falsefor i in range(2, int(num**0.5) + 1): #int函数将结果转换为整数,向下取整if num % i == 0:return Falsereturn True# 使用列表推导式找出1到100的所有素数
prime_numbers = [x for x in range(1, 101) if is_prime(x)]# 打印素数列表
print(prime_numbers)代码执行结果
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]在这段代码中for 循环是素数检查的核心。它从 2 开始(因为 1 不是素数)到 int(num**0.5) + 1 结束。这里使用 num**0.5 是因为一个合数(非素数)必定有一个因子小于或等于它的平方根。int() 函数用来将浮点数转换为整数,确保循环的上限是整数。
2、使用列表推导式,输出200~400之间能被5或6整除的数
输入下面代码
a = [x for x in range(200,401) if x%5==0 or x%6==0]
print(a)代码运行结果
[200, 204, 205, 210, 215, 216, 220, 222, 225, 228, 230,
234, 235, 240, 245, 246, 250, 252, 255, 258, 260, 264,
265, 270, 275, 276, 280, 282, 285, 288, 290, 294, 295,
300, 305, 306, 310, 312, 315, 318, 320, 324, 325, 330,335, 336, 340, 342, 345, 348, 350, 354, 355, 360, 365,366, 370, 372, 375, 378, 380, 384, 385, 390, 395, 396,
400]3、使用集合推导式,输出1~100的所有素数
输入下面代码
方法也和前面一样,只是输出结果为集合
def is_prime(num):if num < 2:return Falsefor i in range(2, int(num**0.5) + 1):if num % i == 0:return Falsereturn True# 使用集合推导式找出1到100的所有素数
prime_numbers_set = {x for x in range(2, 101) if is_prime(x)}# 打印素数集合
print(prime_numbers_set)代码执行结果
{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97}4、使用字典推导式将{”a“:1,”b“:2,“C”:3,“d”:4,”e“:5,”F“:6}的键中小写字母转换为大写字母,大写字母转换为小写字母
输入下面代码
# 原始字典
original_dict = {"a": 1, "b": 2, "C": 3, "d": 4, "e": 5, "F": 6}# 使用字典推导式转换键的大小写
new_dict = {key.swapcase(): value for key, value in original_dict.items()}print(new_dict)代码运行结果
{'A': 1, 'B': 2, 'c': 3, 'D': 4, 'E': 5, 'f': 6}相关文章:

列表、集合、字典的相关练习
1、使用列表推导式,输出1~100的所有素数 输入下面代码 # 定义一个辅助函数用来判断是否是素数 def is_prime(num):if num < 1:return Falsefor i in range(2, int(num**0.5) 1): #int函数将结果转换为整数,向下取整if num % i 0:return Falsere…...
填报志愿选大学专业,文科生如何选专业?
读文科的同学接触的专业知识相对广泛,往往被认为是“万金油”,他们仿佛什么都能做,但是和专业技能类知识不同,缺乏技术支持,从而使得文科专业的就业方向和前景远远比不上理科专业那么明朗,对于众多文科生而…...
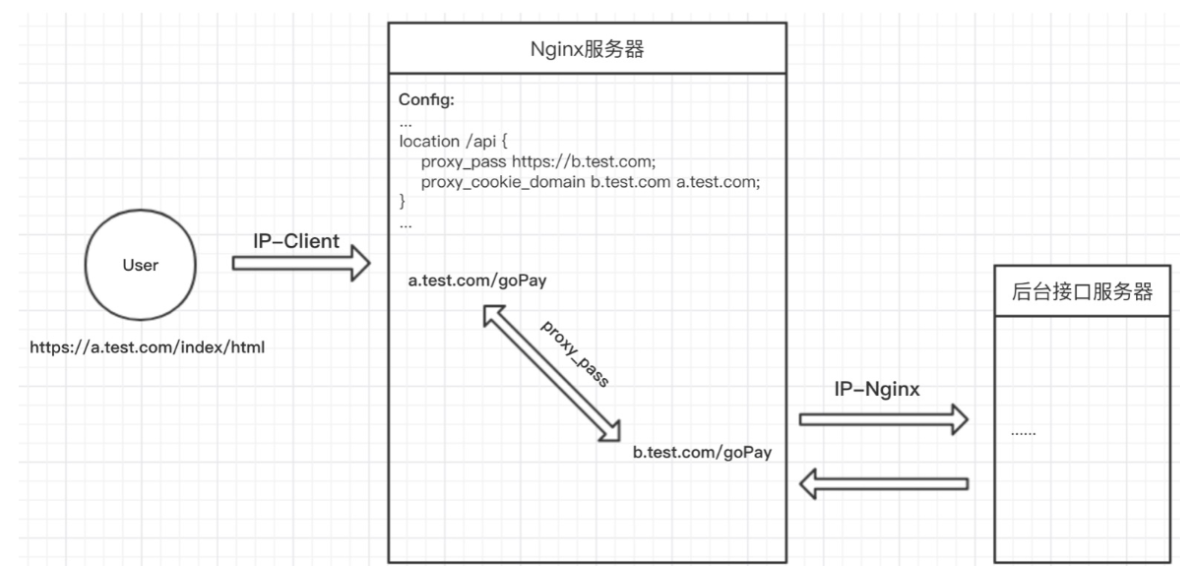
如何实现跨域
如何实现跨域 当浏览器执行JS脚本时,会检测脚本要访问的协议,域名,端口号是不是和当前网址一致,不一致就是跨域。 跨域是不允许的,这种限制叫做浏览器的同源策略,简单就是浏览器不允许一个源加载脚本与其…...

从零开始利用树莓派+扬声器,实现简单的蓝牙音箱,手机连接放歌
背景 树莓派4B自带蓝牙和Wifi, 无需外接 USB dongle; 蓝牙最常见的应用是近距离传输数据,比如蓝牙传文件,蓝牙音箱等。正好家里有个普通的usb供电的便携音箱; 本文用树莓派蓝牙+普通音箱,实现简单的蓝牙音箱。 大致分为三个部分: kernel/driver层的ALSA驱动框架蓝牙音…...

今年的就业环境不容乐观,你想好怎么应对了吗
今年的就业环境不容乐观,你想好怎么应对了吗 毕业生进入职场的历程往往充满挑战和未知,尤其是在当前经济环境下,失业问题愈发凸显。本文通过分享几位年轻人的真实经历,剖析大学生及职场人士面临的困境,并提供应对策略…...
测试 halcon measure_projection 算子
期望结果完全相同,但是下面的测试结果和halcon的差值如下: [0.132838, 0.231991, 0.265157, 0.296903, 0.0998573, 0.165907, 0.230686, 0.130266, 0.0977104, 0.197109, 0.198173, 0.197086, 0.190943, 0.177665, 0.163521, 0.146541, 0.161362, 0.166666, 0.2281…...
反爬原理和解决方法,不然你的Python会有Bug)
网络安全岗位必须知道到:高性能抓取,多线程,异步逆向分析(Js逆向破解/APP逆向破解)反爬原理和解决方法,不然你的Python会有Bug
JS逆向破解和APP逆向破解以及反爬技术是网络安全和数据保护领域的重要话题。 遵循安全开发的最佳实践,包括输入验证、数据加密、权限管理等,以减少安全漏洞的出现。 坚决维护网络安全及开发安全,杜绝一切被爬,非法爬取数据的行为…...

lua网站开发中如何制作自定义模块
自定义模块是FastWeb框架的重要拓展功能,用来扩展和增强服务的能力。通过自定义模块,开发者可以轻松添加特定的功能和特性,使得网站开发更加灵活和高效。本文将演示如何添加自己的模块作为FastWeb的拓展,为框架的壮大与支持提供重…...
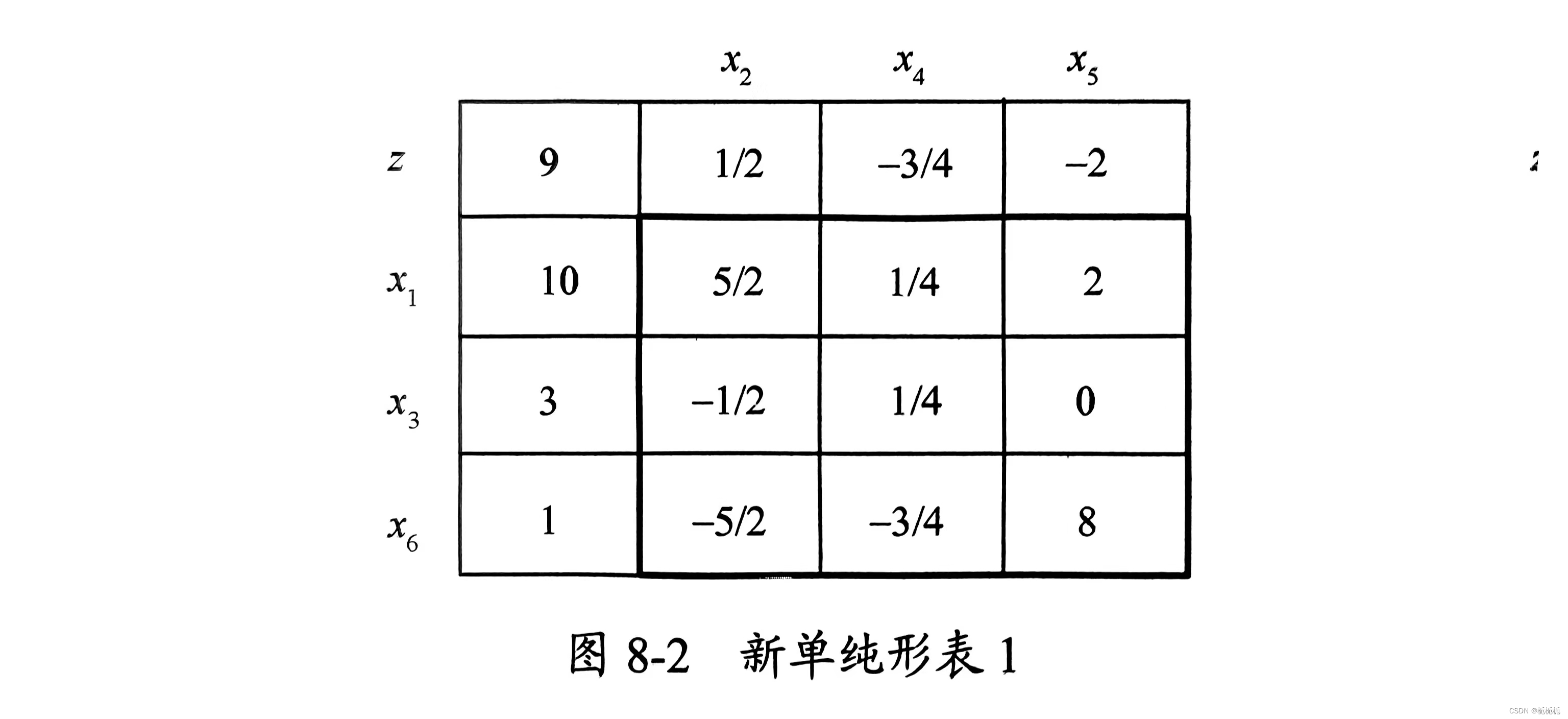
线性规划问题——单纯形算法
第一步:化“约束标准型” 在每个等式约束中至少有一个变量的系数为正,且这个变量只在该约束中出现。在每个约束方程中选择一个这样的变量称为基本变量。 剩下变量称为非基本变量。 一个简单的栗子 上图是一个约束标准型线性规划的例子。 等式1&#x…...
ADS基础教程20 - 电磁仿真(EM)参数化
EM介绍 一、引言二、参数化设置1.参数定义2.参数赋值3.创建EM模型和符号 四、总结 一、引言 参数化EM仿真,是在Layout环境下创建参数,相当于在原理图中声明变量。 二、参数化设置 1.参数定义 1)在Layout视图,菜单栏中选中EM&g…...
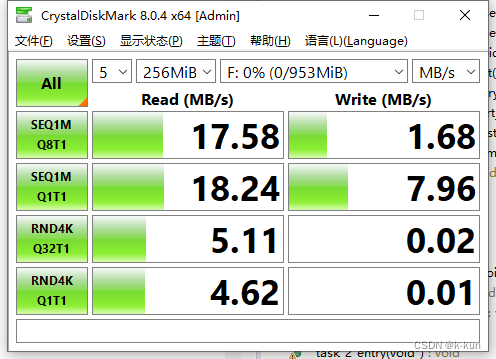
NAND flash测试-雷龙发展
文章目录 一、简介 二、速度测试 最近比较忙,也一直没空发什么文章,这算是新年第一篇吧,正好最近收到了一个雷龙的flash芯片,先拿来玩一下吧。 有兴趣的小伙伴可以去雷龙官网找小姐姐领取一个免费试用。 一、简介 大概样子就是上面…...

CMake的学习之路
目录 一、基础命令 二、编译选项和设置 三、文件和目录操作 四、控制流命令 五、其他命令 六、CMake构建级别 CMake是一个跨平台的自动化建构系统,它使用一种人类可读的配置文件(CMakeLists.txt)来控制软件编译过程。以下是CMake中的一些…...
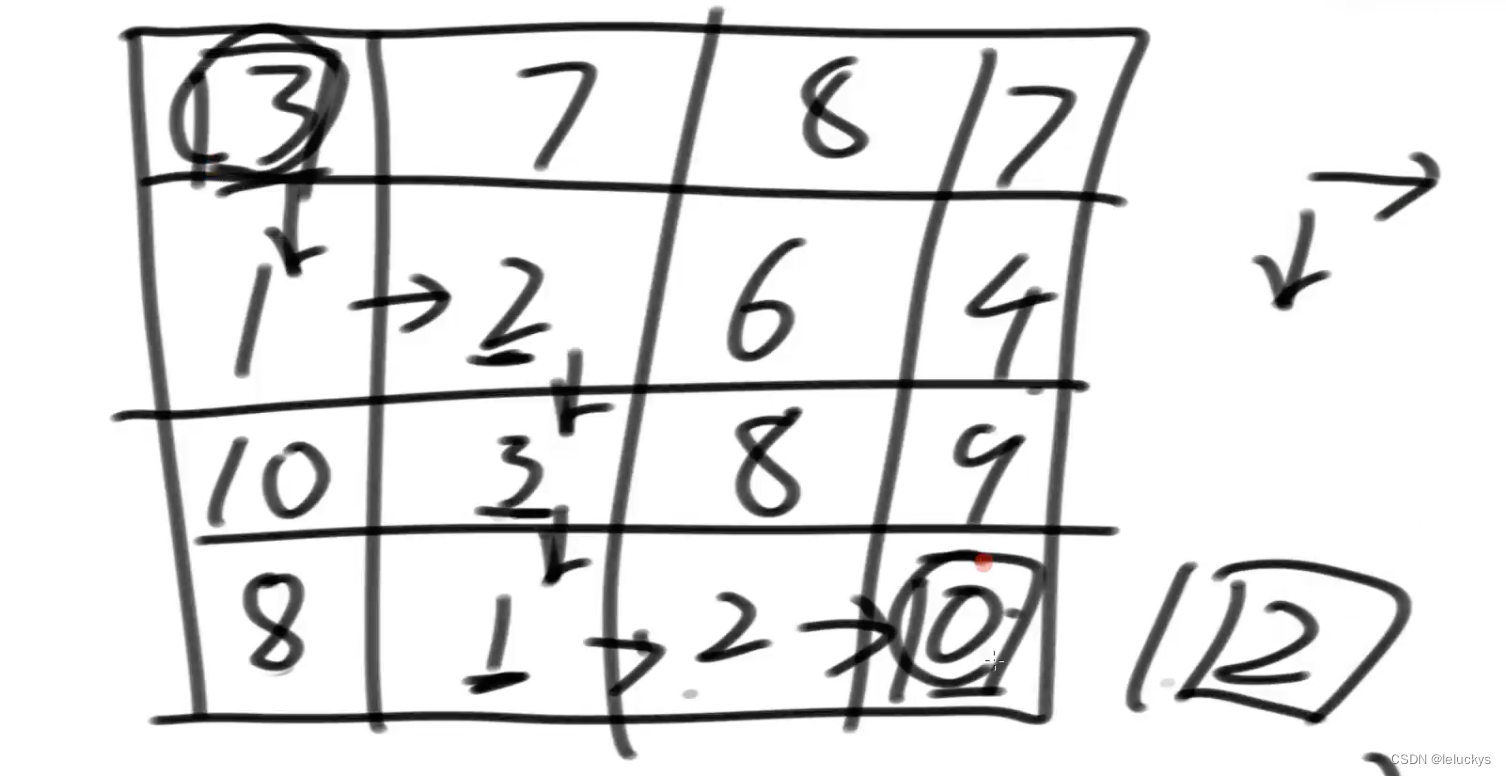
算法体系-22 第二十二节:暴力递归到动态规划(四)
一 最小距离累加和 1.1 描述 给定一个二维数组matrix,一个人必须从左上角出发,最后到达右下角 沿途只可以向下或者向右走,沿途的数字都累加就是距离累加和 返回最小距离累加和 1.2 分析...
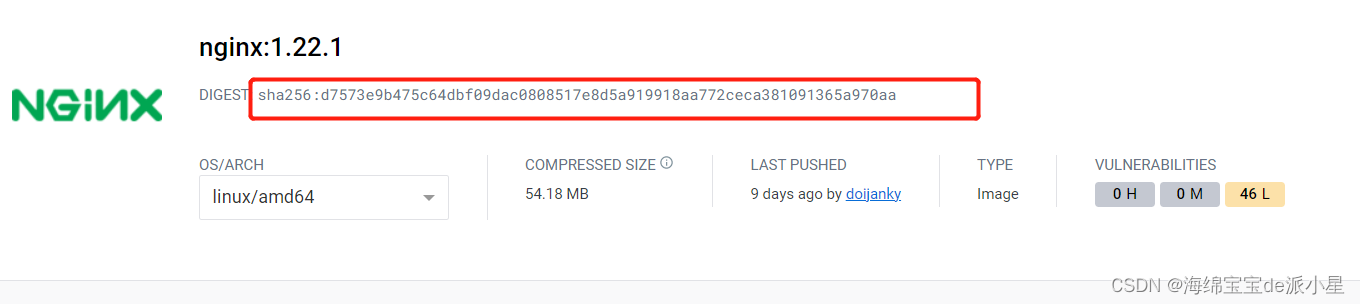
Docker:利用Docker搭建一个nginx服务
文章目录 搭建一个nginx服务认识nginx服务Web服务器反向代理服务器高性能特点 安装nginx启动nginx停止nginx查找nginx镜像拉取nginx镜像,启动nginx站点其他方式拉取nginx镜像信息通过 DIGEST 拉取镜像 搭建一个nginx服务 首先先认识一下nginx服务: NGI…...

docker Pulling fs layer 含义
在使用Docker时,当你执行 docker pull 命令来获取一个新的镜像,控制台输出中可能会出现 "Pulling fs layer" 的信息。这是Docker拉取镜像过程中的一个步骤,下面是对这一过程的解释: Docker 镜像是由一系列的层…...
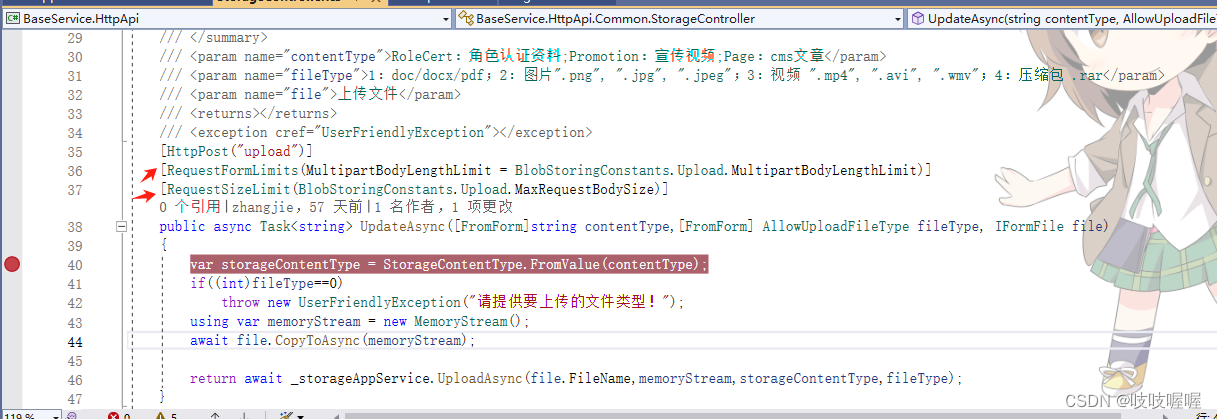
c#中上传超过30mb的文件,接口一直报404,小于30mb的却可以上传成功
在一次前端实现上传视频文件时,超过30mb的文件上传,访问接口一直报404,但是在Swagger中直接访问接口确是正常的,且在后端控制器中添加了限制特性,如下 但是却仍然报404,在apifox中请求接口也是报404, 网上说: 在ASP.NET Core中,配置请求过来的文件上传的大小限制通常…...
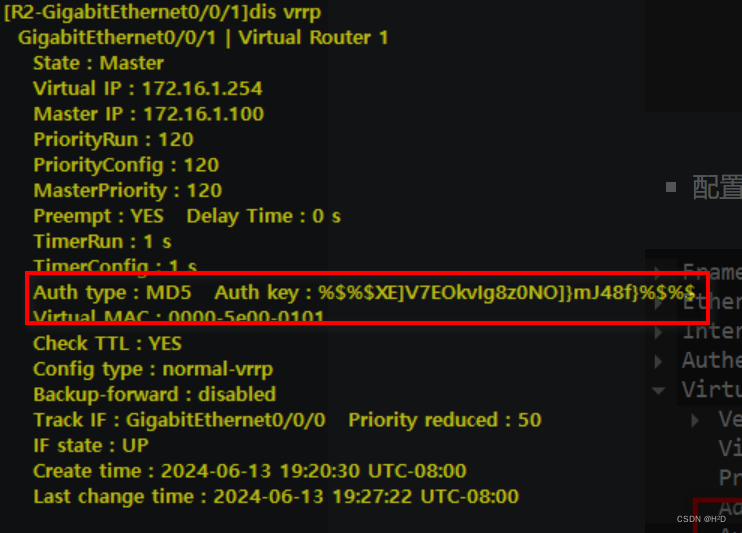
VRRP跟踪接口及认证(华为)
#交换设备 VRRP跟踪接口及认证 一、相关概念 1.VRRP跟踪接口 当 VRRP 的 Master 设备的上行接口出现问题, 而 Master 设备一直保持 Active 状态,那么就会导致网络出现中断,所以必须要使得 VRRP 的运行状态和上行接口能够关联。在配置了 VRRP 元余的网…...
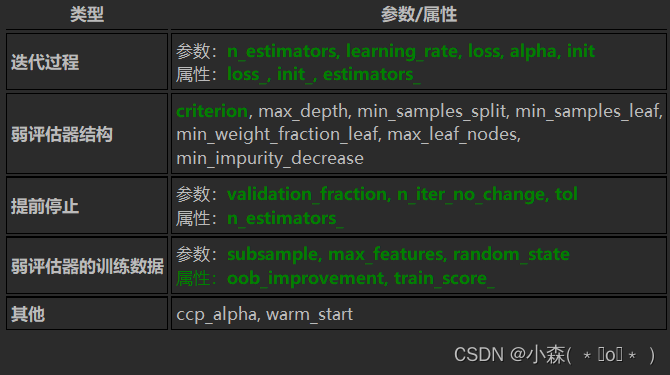
梯度提升树GBDT系列算法
Boosting方法的基本元素与基本流程💫 在Boosting集成算法当中,我们逐一建立多个弱评估器(基本是决策树),并且下一个弱评估器的建立方式依赖于上一个弱评估器的评估结果,最终综合多个弱评估器的结果进行输出…...

探索智慧农业系统架构的设计与应用
随着科技的不断进步和农业现代化的推进,智慧农业正逐渐成为农业发展的重要趋势。智慧农业系统架构的设计与应用,将农业生产与信息技术相结合,为农业生产提供了新的思路和解决方案。本文将深入探讨智慧农业系统架构的设计与应用,从…...

【C语言】一篇文章带你深度理解函数
目录 1. 函数的概念 2. 库函数 2.1 标准库和头文件 2.2 库函数的使用方法 2.2.1 举例 sqrt 2.2.2 库函数文档的一般格式 3. 自定义函数 3.1 函数的语法形式 3.2 函数的举例 4. 形参和实参 4.1 实参 4.2 形参 4.3 实参和形参的关系 5. …...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...
