线性规划问题——单纯形算法
第一步:化“约束标准型”
在每个等式约束中至少有一个变量的系数为正,且这个变量只在该约束中出现。在每个约束方程中选择一个这样的变量称为基本变量。
剩下变量称为非基本变量。
一个简单的栗子
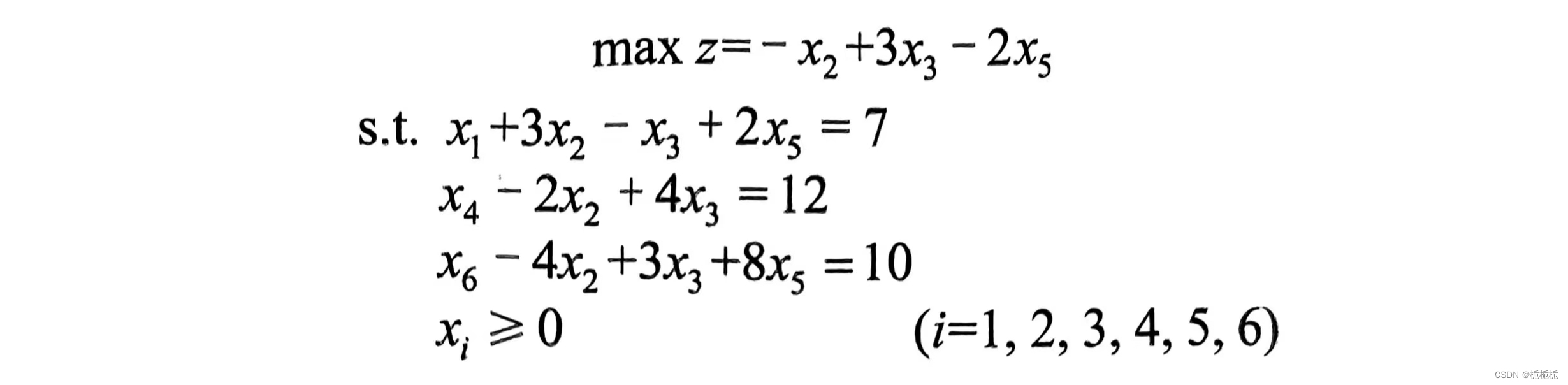
上图是一个约束标准型线性规划的例子。
等式1:x₁+3x₂-x₃+2x₅=7
x₁,x₂,x₅ 的系数为正,但是等式2和3中有 x₂,等式3中有 x₅;所以等式1的基本变量是 x₁。
等式2:x₄-2x₂+4x₃=12
x₄,x₃ 的系数为正,但是等式1和3中都有 x₃;所以等式1的基本变量是 x₄。
等式3:x₆-4x₂+3x₃+8x₅=10
x₆,x₃,x₅ 的系数为正,但是等式1和2中都有 x₃,等式1中有 x₅;所以等式1的基本变量是 x₆。
那么,x₁,x₄,x₆ 是基本变量;剩下的x₂,x₃,x₅ 是非基本变量。
————————简陋的分割线————————
如果我们让非基本变量 x₂,x₃,x₅ 都等于 0 呢?
式子就变成了下面介个样子。
maxz=0
x₁=7
x₄=12
x₆=10其中x₁=7,x₄=12,x₆=10,x₂=0,x₃=0,x₅=0。
所以,将所有非基本变量置为 0,从约束方程式中解出满足约束的基本条件的值,即可求出一个基本可行解。当然,这个基本可行解未必是最优解。
而且,很明显,解等于该式子的常数部分。
————————简陋的分割线————————
单纯形算法的基本思想就是从一个基本可行解出发,进行一系列的基本可行解的变换。每次变换将一个非基本变量与一个基本变量互调位置,且保持当前的线性规划问题是一个与原问题完全等价的标准型线性规划问题。(不懂的话继续往下看就懂啦~)
第二步:列初始单纯形表
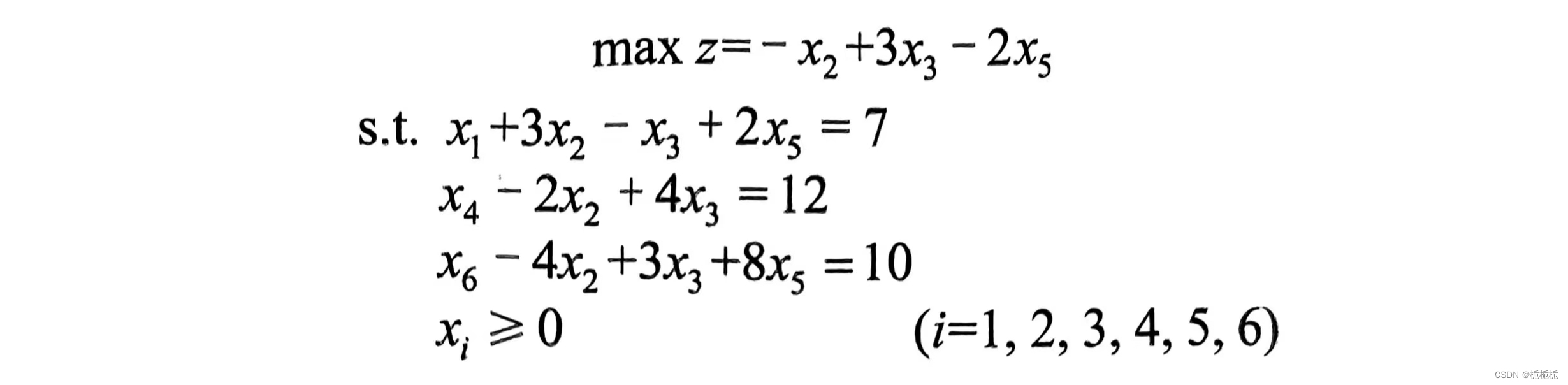
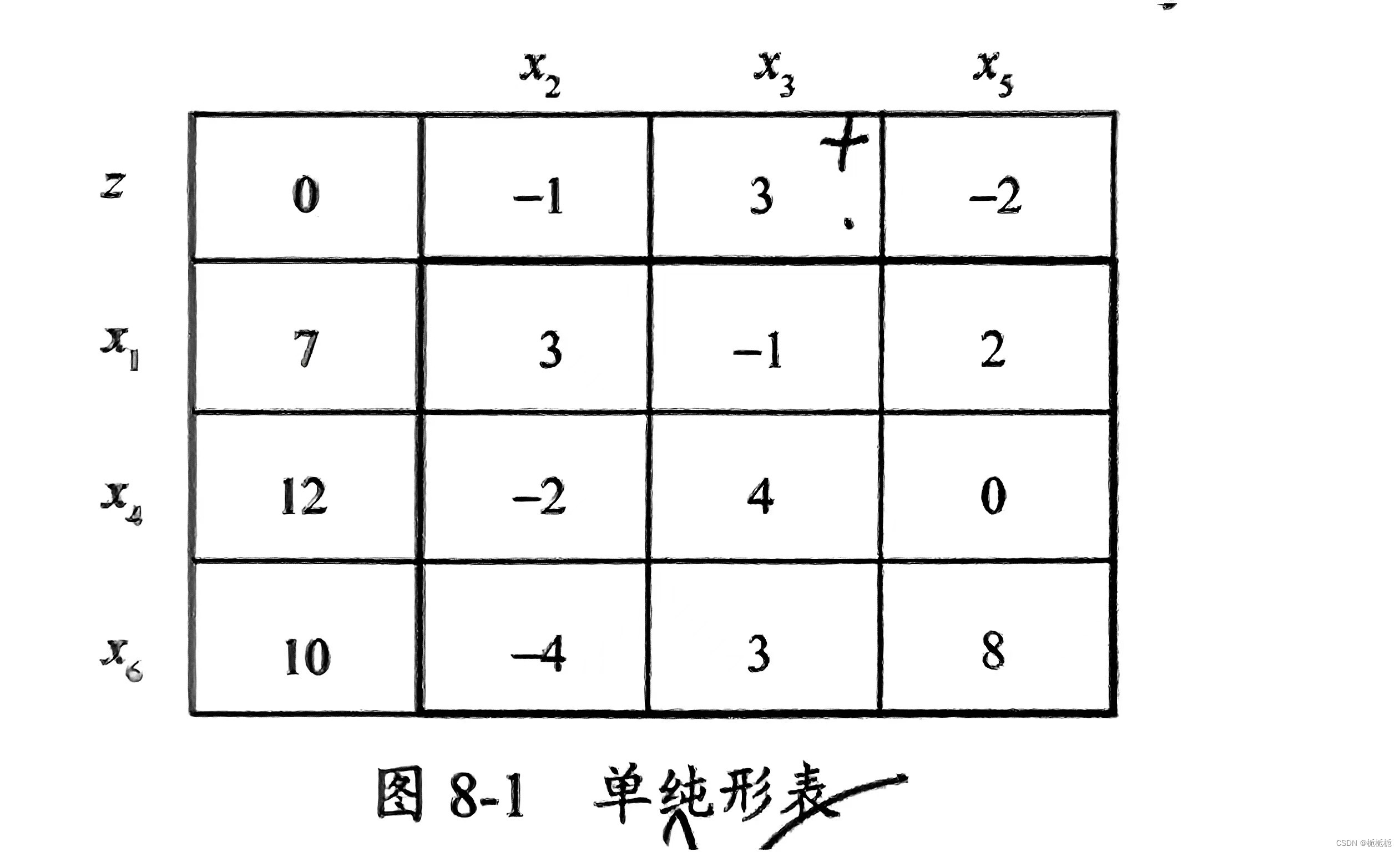
很明显,红色部分基本变量,蓝色部分非基本变量。
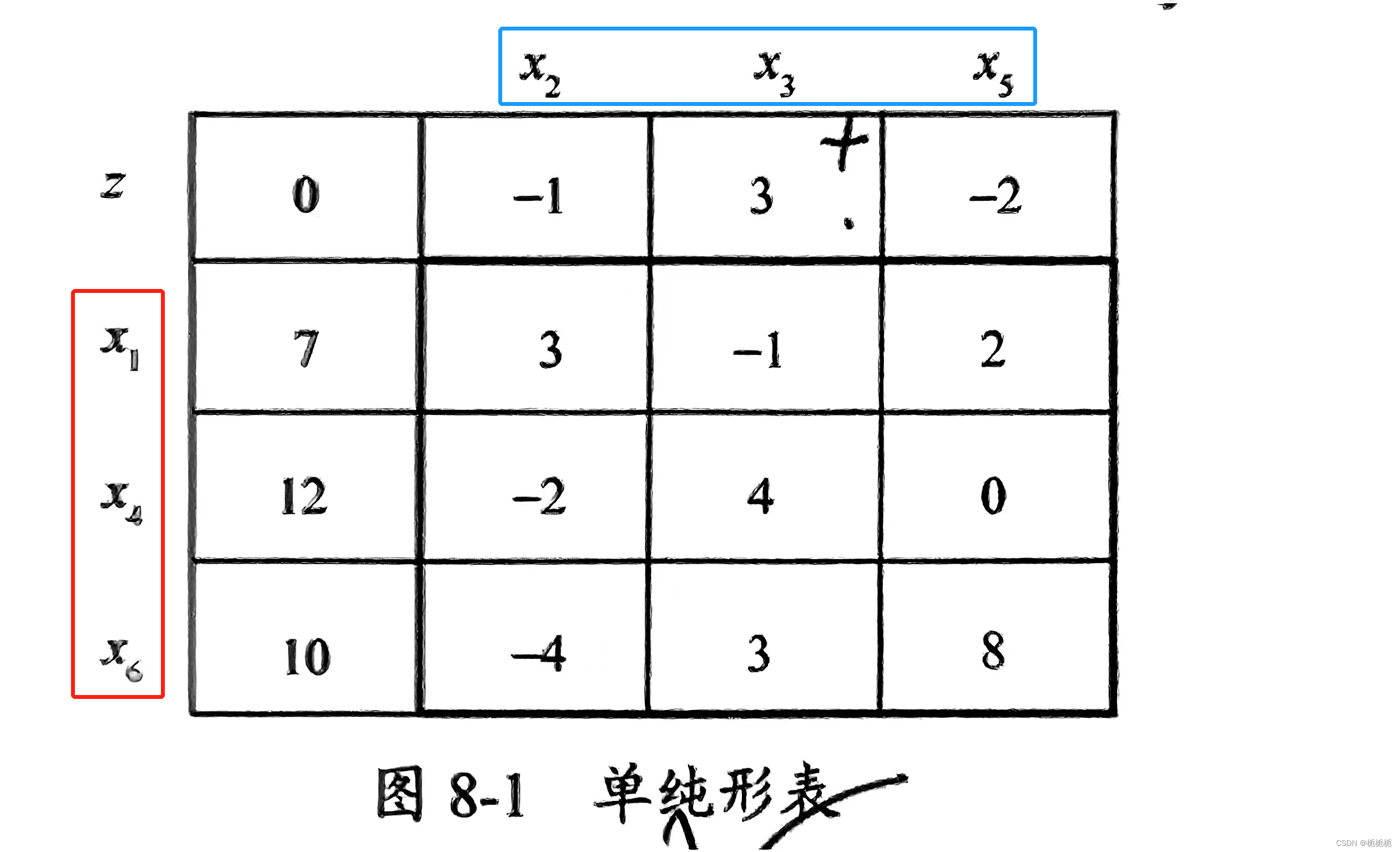
其中的 0,7,12,10 是常数项;剩下的是系数项。(很简单的填表不赘述了)
————————简陋的分割线————————
接下来是选择入基变量和离基变量
入基变量从非基本变量里选
红框里选正的,红框里选正的,红框里选正的。所以选 x₃为入基变量;
如果没有系数为正的,那么当前基本可行解为最优解。
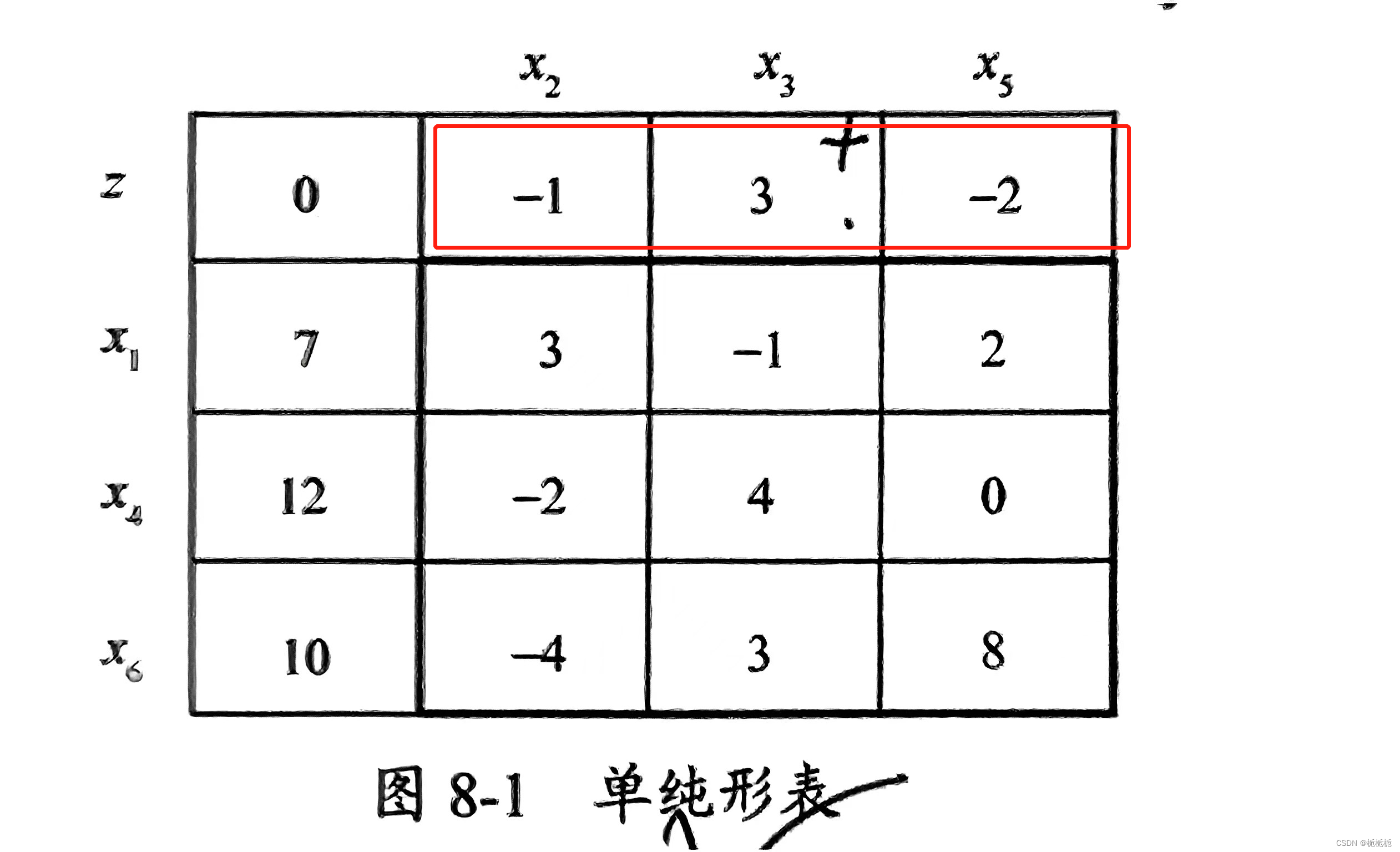
离基变量从基本变量里选
在前面我们选择了唯一的正值元素3,它所在的列中有两个正元素,4和3。
我们算min{12/4,10/3}=3,所以选 x₄ 为离基变量。
如果3所在的列没有正元素,那么最优解无界,计算结束。
第三步:基变换直到找到最优解
然后做转轴变换,目的是将入基变量与离基变量互调位置。
x₄-2x₂+4x₃=12
x₃ , x₄ 变换。
x₃-x₂/2+x₄/4=3
代入x₁+3x₂-x₃+2x₅=7 和 x₆-4x₂+3x₃+8x₅=10 消去x₃。
x₁+5x₂/2+x₄/4+2x₅=10
x₆-5x₂/2-3x₄/4+8x₅=1
代入目标函数。
maxz=9+x₂/2-3x₄/4-2x₅
形成的新单纯形表如下
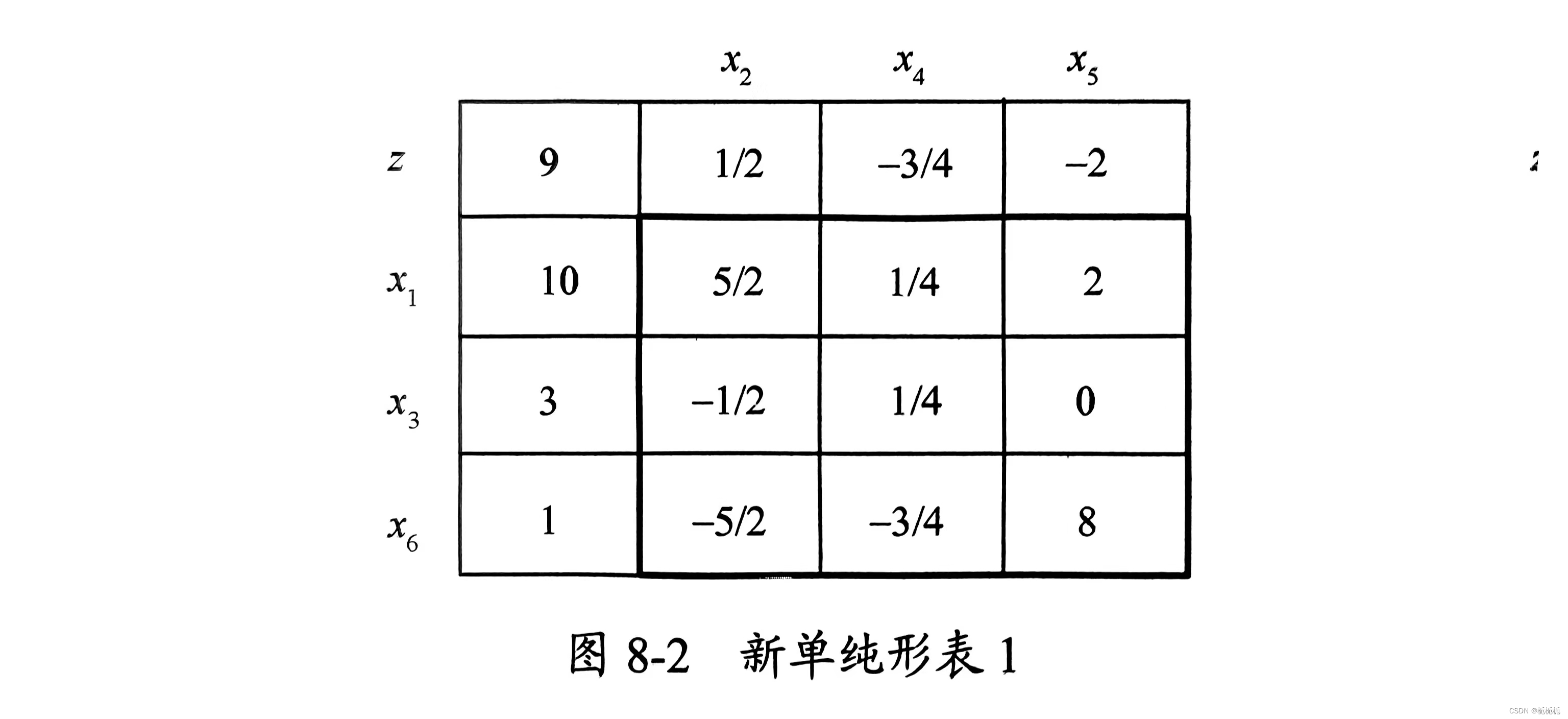
形成新的单纯形表,重复前面过程,直到所有非基本变量系数都变为负值为止。
相关文章:

线性规划问题——单纯形算法
第一步:化“约束标准型” 在每个等式约束中至少有一个变量的系数为正,且这个变量只在该约束中出现。在每个约束方程中选择一个这样的变量称为基本变量。 剩下变量称为非基本变量。 一个简单的栗子 上图是一个约束标准型线性规划的例子。 等式1&#x…...
ADS基础教程20 - 电磁仿真(EM)参数化
EM介绍 一、引言二、参数化设置1.参数定义2.参数赋值3.创建EM模型和符号 四、总结 一、引言 参数化EM仿真,是在Layout环境下创建参数,相当于在原理图中声明变量。 二、参数化设置 1.参数定义 1)在Layout视图,菜单栏中选中EM&g…...
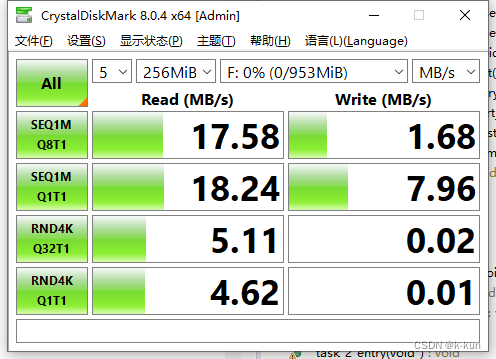
NAND flash测试-雷龙发展
文章目录 一、简介 二、速度测试 最近比较忙,也一直没空发什么文章,这算是新年第一篇吧,正好最近收到了一个雷龙的flash芯片,先拿来玩一下吧。 有兴趣的小伙伴可以去雷龙官网找小姐姐领取一个免费试用。 一、简介 大概样子就是上面…...

CMake的学习之路
目录 一、基础命令 二、编译选项和设置 三、文件和目录操作 四、控制流命令 五、其他命令 六、CMake构建级别 CMake是一个跨平台的自动化建构系统,它使用一种人类可读的配置文件(CMakeLists.txt)来控制软件编译过程。以下是CMake中的一些…...
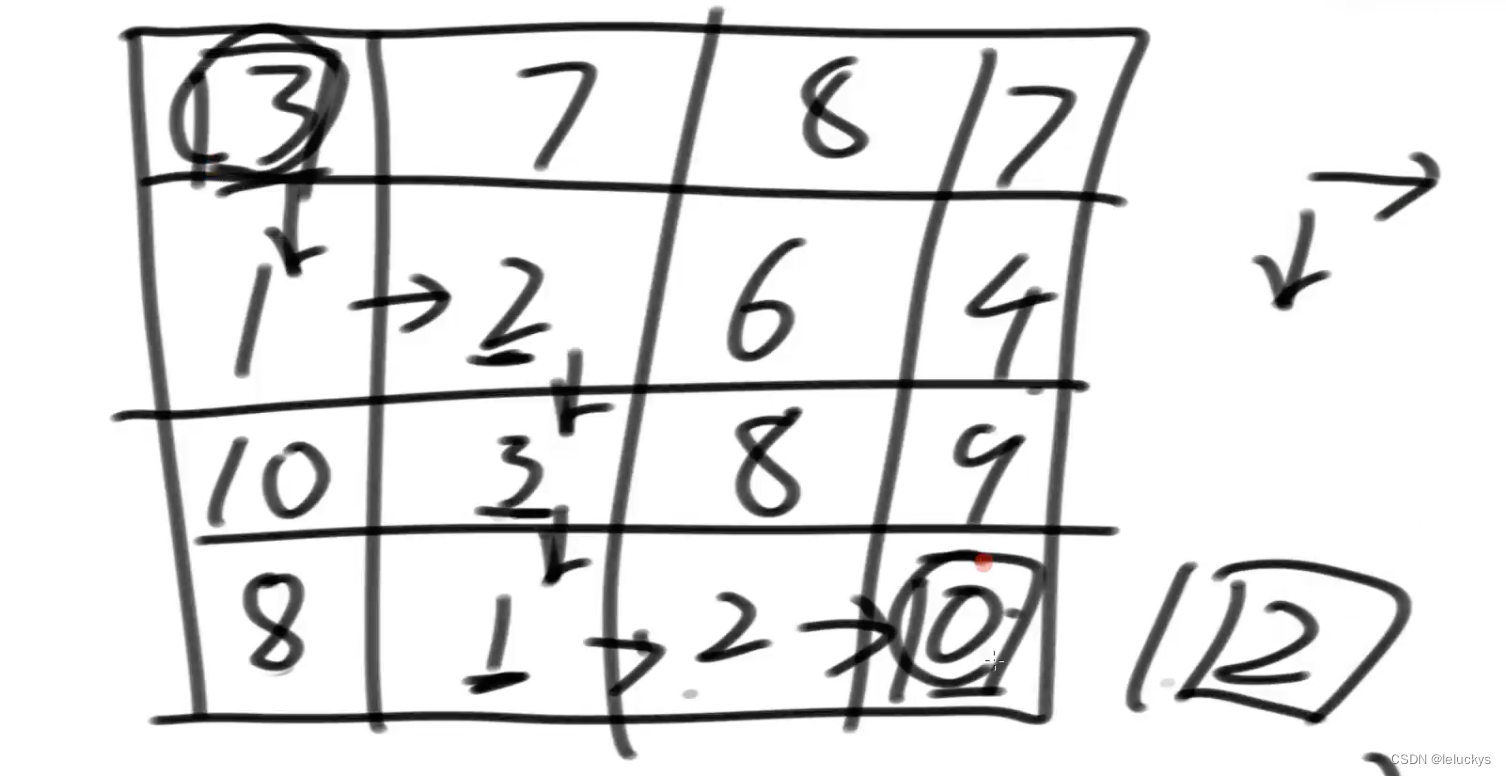
算法体系-22 第二十二节:暴力递归到动态规划(四)
一 最小距离累加和 1.1 描述 给定一个二维数组matrix,一个人必须从左上角出发,最后到达右下角 沿途只可以向下或者向右走,沿途的数字都累加就是距离累加和 返回最小距离累加和 1.2 分析...
Docker:利用Docker搭建一个nginx服务
文章目录 搭建一个nginx服务认识nginx服务Web服务器反向代理服务器高性能特点 安装nginx启动nginx停止nginx查找nginx镜像拉取nginx镜像,启动nginx站点其他方式拉取nginx镜像信息通过 DIGEST 拉取镜像 搭建一个nginx服务 首先先认识一下nginx服务: NGI…...

docker Pulling fs layer 含义
在使用Docker时,当你执行 docker pull 命令来获取一个新的镜像,控制台输出中可能会出现 "Pulling fs layer" 的信息。这是Docker拉取镜像过程中的一个步骤,下面是对这一过程的解释: Docker 镜像是由一系列的层…...
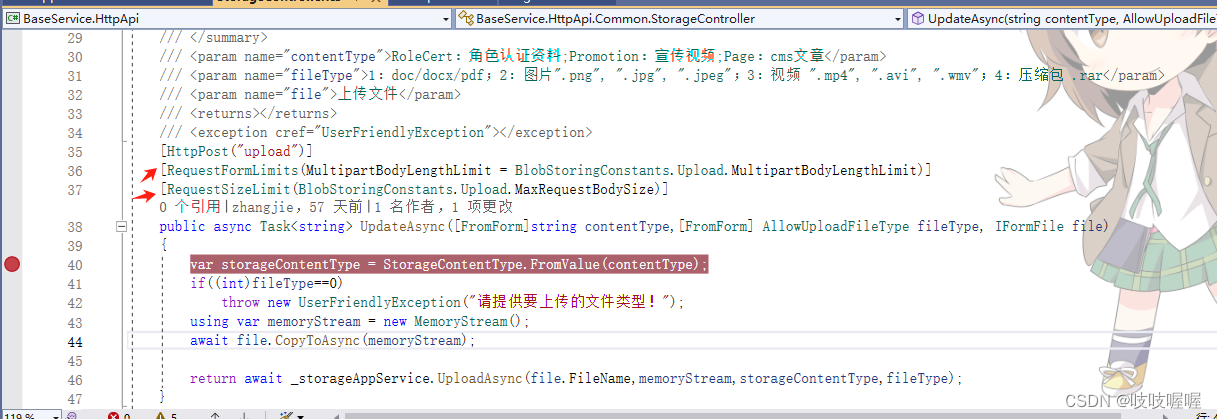
c#中上传超过30mb的文件,接口一直报404,小于30mb的却可以上传成功
在一次前端实现上传视频文件时,超过30mb的文件上传,访问接口一直报404,但是在Swagger中直接访问接口确是正常的,且在后端控制器中添加了限制特性,如下 但是却仍然报404,在apifox中请求接口也是报404, 网上说: 在ASP.NET Core中,配置请求过来的文件上传的大小限制通常…...
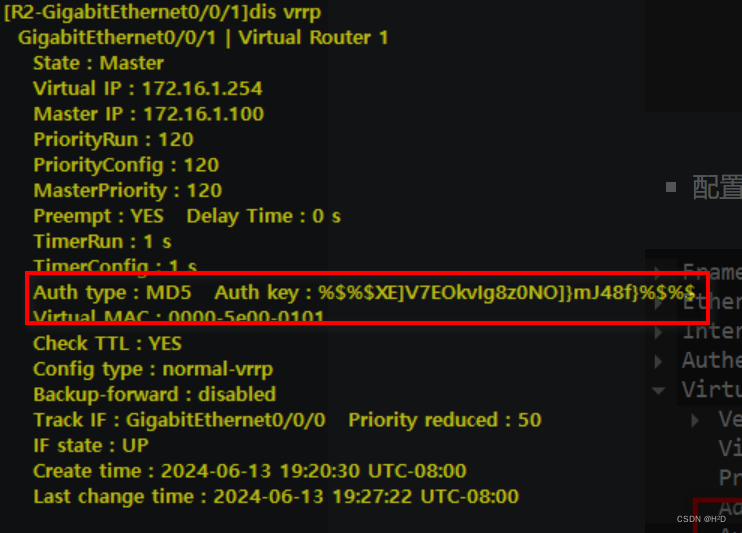
VRRP跟踪接口及认证(华为)
#交换设备 VRRP跟踪接口及认证 一、相关概念 1.VRRP跟踪接口 当 VRRP 的 Master 设备的上行接口出现问题, 而 Master 设备一直保持 Active 状态,那么就会导致网络出现中断,所以必须要使得 VRRP 的运行状态和上行接口能够关联。在配置了 VRRP 元余的网…...
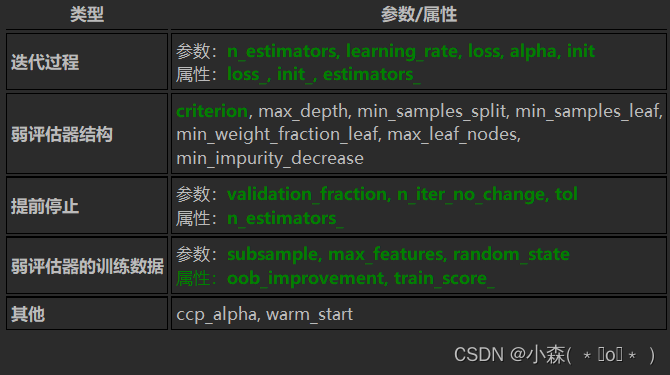
梯度提升树GBDT系列算法
Boosting方法的基本元素与基本流程💫 在Boosting集成算法当中,我们逐一建立多个弱评估器(基本是决策树),并且下一个弱评估器的建立方式依赖于上一个弱评估器的评估结果,最终综合多个弱评估器的结果进行输出…...

探索智慧农业系统架构的设计与应用
随着科技的不断进步和农业现代化的推进,智慧农业正逐渐成为农业发展的重要趋势。智慧农业系统架构的设计与应用,将农业生产与信息技术相结合,为农业生产提供了新的思路和解决方案。本文将深入探讨智慧农业系统架构的设计与应用,从…...

【C语言】一篇文章带你深度理解函数
目录 1. 函数的概念 2. 库函数 2.1 标准库和头文件 2.2 库函数的使用方法 2.2.1 举例 sqrt 2.2.2 库函数文档的一般格式 3. 自定义函数 3.1 函数的语法形式 3.2 函数的举例 4. 形参和实参 4.1 实参 4.2 形参 4.3 实参和形参的关系 5. …...

荣耀手机删除系统APP
1、打开开发者模式 设置–系统–关于手机–快速多次点击手机的版本号,即可进入开发者模式。 然后进入开发人员选项,开启USB调试,如下图。 2、数据线连接电脑,检查设备连接情况 按键盘winR键,在弹窗中输入cmd&#…...

vue+elementui+springboot图片上传
1、前端代码 <template><div><el-uploadclass"avatar-uploader"action"http://localhost:8081/ch06/demo/uploadAvatar":show-file-list"false":on-success"handleAvatarSuccess":before-upload"beforeAvatarUpl…...

路由器怎么设置局域网?
局域网(Local Area Network,LAN)是指在一个相对较小的地理范围内,如家庭、办公室或学校等,通过路由器等设备连接起来的计算机网络。设置局域网可以方便地实现内部资源共享和信息交流。本文将介绍如何设置局域网以及一个…...

Linux2(文件类型分类 基本命令2 重定向)
目录 一、文件类型分类 二、基本命令2 1. find 帮助查询 2. stat 查看文件的信息 3. wc 统计文本 4. 查看文本内容 4.1 cat 4.2 more 4.3 less 4.4 head 4.5 tail 5. cal 显示日历 6. date 显示时间 7. du 文件大小 8. ln 链接 软链接 硬链接 区别 9. histo…...
c->c++(一):部分KeyWord
本文主要探讨c相关关键字的使用。 char char默认是unsigned/signed取决平台,wchar_t宽字符:用于Unicode编码(超过一个字节),用wcin和wcout输入输出,字符串为wstring char8_t(20),char16_t(11起),char32_t(11):指定占用字节数且是无符号,字符串类u8string,u16s…...

【iOS】YYModel源码阅读笔记
文章目录 前言一、JSON转换库对比二、YYModel性能优化三、YYModel的使用四、架构分析YYClassInfo 剖析 五、流程剖析转换前准备工作 – 将JSON统一成NSDictionary将NSDictionary 转换为Model对象提取Model信息使用NSDictionary的数据填充Model 总结 前言 先前写了JSONModel的源…...

C++Qt做一个鼠标在按钮上悬浮3s显示一个悬浮窗口
当你想要在 Qt 中创建一个自定义按钮并添加悬浮窗口的功能时,你可以通过继承 QPushButton 类来实现。下面是一个示例代码,演示了如何创建一个自定义按钮类 HoverButton,并在鼠标悬浮在按钮上 3 秒后显示一个悬浮窗口,窗口包含图片…...
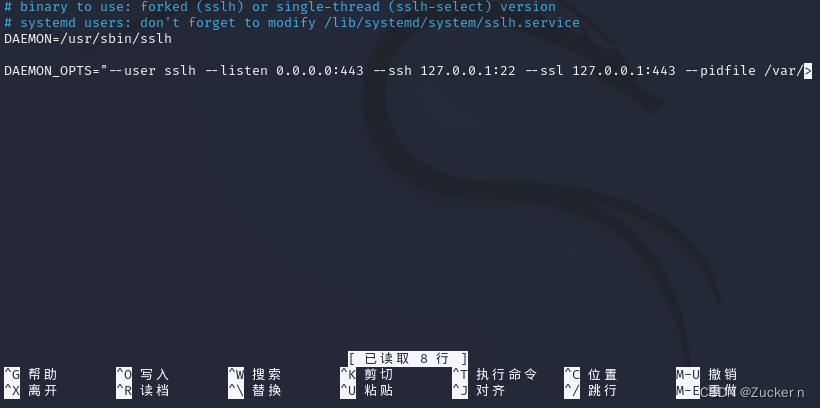
sslh一键在一个端口上运行多个服务(KALI工具系列二十三)
目录 1、KALI LINUX 简介 2、sslh工具简介 3、信息收集 3.1 目标主机IP(win) 3.2 KALI的IP 4、操作示例 4.1 监听特定端口 4.2 配置SSH 4.3 配置apache 4.4 配置sshl 4.5 验证配置 5、总结 1、KALI LINUX 简介 Kali Linux 是一个功能强大、…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...
