代码随想录算法训练营Day38|动态规划理论基础、2.斐波那契数、3.爬楼梯、4.使用最小花费爬楼梯
动态规划理论基础
代码随想录 (programmercarl.com)
动态规划(Dynamic Programming,简称DP)是一种算法设计技术,它通过将复杂问题分解为更小的子问题来解决优化问题。动态规划通常用于解决那些具有重叠子问题和最优子结构特性的问题。(可以理解为一种递推)
重叠子问题:
在递归算法中,相同的子问题会被多次计算。动态规划通过存储这些子问题的解来避免计算。这个存储通常使用一个表格(数组)来实现,称为备忘录或DP表。
最优子结构:
一个问题的最优解包含其子问题的最优解。这意味着可以通过组合子问题的最优解来构造原问题的最优解。
动态规划的通常步骤:
- 定义状态:确定DP数组的含义,即dp[i]通常代表什么意义,比如在斐波那契数列问题中,dp[i]代表第i个斐波那契数。
- 状态转移方法:确定状态之间如何转移,即如何从一个或多个已知状态的值计算出下一个状态的值,如斐波那契数中 F[i] = F[i-1] + F[i-2]。
- 初始化:确定DP数组的初始值,这些通常关乎问题的边界条件。如斐波那契数中F[0] = 0,F[1] = 1。
- 计算顺序:确定DP数组的计算顺序,通常需要按照逻辑顺序从小到大计算。如斐波那契数列需要一次从2开始向后计算得到想要的值。
- 返回结果:根据DP数组的最终值来确定原问题的解。如返回你需要的斐波那契数。
斐波那契数
509. 斐波那契数 - 力扣(LeetCode)
递推顺序为 F(n) = F(n-1)+F(n-2)
F(0) = 0, F(1) = 1
class Solution {
public:int fib(int n) {// 如果 n 小于或等于 1,直接返回 n// 这是因为斐波那契数列的前两个数是定义好的:F(0) = 0, F(1) = 1if(n<=1) return n;// 创建一个动态数组 dp,大小为 n+1,用于存储斐波那契数列vector<int>dp(n+1);// 初始化 dp 数组的前两个数,即 F(0) 和 F(1)dp[0] = 0;dp[1] = 1;// 从 2 开始循环到 n,计算 dp 数组的其余值for(int i = 2; i <= n; i++){// 根据斐波那契数列的定义,每个数是前两个数的和dp[i] = dp[i-1]+ dp[i-2];}// 返回 dp 数组的最后一个值,即斐波那契数列的第 n 个数return dp[n];}
};
算法的时间复杂度为O(n),空间复杂度同样为O(n),需要维护一个斐波那契数数组。
爬楼梯
70. 爬楼梯 - 力扣(LeetCode)
斐波那契数的一个变体,开始没想到,想到之后只能感慨代码随想录的题目顺序还是很用心的。
假设爬到第i-1层有x种方案,爬到第i-2层有y种方案,那么爬到第i层有x+y种方案(第i-1层再向上爬一层达到i,第i-2层向上爬2层到达i层)。由此,就能看出这个问题是上述斐波那契数的变体。递推关系为dp[i] = dp[i-1] + dp[i-2],从前往后遍历,dp[0] = 0,dp[1] = 1,爬到1层只有一种方案,dp[2] =2,爬到2层有2种可能 1 1 和 2。具体代码如下,我考虑从3开始计算,最后返回dp[n]。
class Solution {
public:// 定义一个名为 climbStairs 的函数,用于计算爬到第 n 阶楼梯的方法数int climbStairs(int n) {// 如果 n 小于或等于 2,直接返回 n// 这是因为当楼梯阶数不超过 2 时,方法数与楼梯阶数相同if(n<=2) return n;// 创建一个动态数组 dp,大小为 n+1,用于存储到达每一阶楼梯的方法数vector<int>dp(n+1);// 初始化 dp 数组的前三个数,即到达第 0、1、2 阶的方法数// 到达第 0 阶的方法数为 0,因为还没有开始爬,这里也可以认为是1,能减少一点代码量 // 这样dp[2]不用赋值dp[0] = 0;// 到达第 1 阶的方法数为 1,只能爬 1 阶dp[1] = 1;// 到达第 2 阶的方法数为 2,可以一次爬 2 阶或者分两次各爬 1 阶dp[2] = 2;// 从 3 开始循环到 n,计算 dp 数组的其余值for(int i = 3; i <= n; i++){// 根据问题的性质,到达第 i 阶的方法数是到达第 i-1 阶和第 i-2 阶的方法数之和// 这是因为每次你可以选择爬 1 阶或 2 阶,所以到达第 i 阶的方法可以从第 i-1 阶爬上来,或者从第 i-2 阶爬上来dp[i] = dp[i-1] + dp[i-2];}// 返回 dp 数组的最后一个值,即到达第 n 阶的方法数return dp[n];}
};
算法的时间复杂度为O(n),空间复杂度同样为O(n),需要维护一个斐波那契数数组。
使用最小花费爬楼梯
746. 使用最小花费爬楼梯 - 力扣(LeetCode)
这里同样是上述问题的变种,但需要考虑的是,这里不是找方案,而是计算损失,所以动态规划数组dp[i]代表的是到达n前的最小花费,到达第i层需要分别计算到达第i-1层和到达第i-2层的损失,然后选择较小的值作为dp[i]的值。由于在到达最终的n层前,每次到达一个i都需要起跳,所以需要添加损失,dp[i]为min(dp[i-1]+cost[i],dp[i-2]+cost[i]),而最后抵达n时,不再需要起跳,只需要考虑dp[n-1]和dp[n-2]的较小值,就是爬楼梯所需的最小花费。
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {// 获取楼梯的阶数,即成本数组的大小int n = cost.size();// 创建一个动态数组 dp,大小为 n,用于存储到达每一阶楼梯的最小成本vector<int>dp(n);// 初始化 dp 数组的前两个数,即到达第 0、1 阶的最小成本// 到达第 0 阶的成本就是 cost[0]dp[0] = cost[0];// 到达第 1 阶的成本就是 cost[1]dp[1] = cost[1];// 从第 2 阶开始循环到第 n-1 阶,计算 dp 数组的其余值for(int i = 2; i < n; i++){// 到达第 i 阶的最小成本是到达第 i-1 阶和第 i-2 阶的最小成本加上当前阶梯的成本中的较小值// 这是因为每次你可以选择从第 i-1 阶爬上来或者从第 i-2 阶爬上来dp[i] = min(dp[i-1] + cost[i], dp[i-2] + cost[i]);}// 最后,到达楼顶的最小成本是到达倒数第一阶和倒数第二阶的最小成本中的较小值// 因为你可以从倒数第一阶直接到达楼顶,也可以从倒数第二阶直接到达楼顶return min(dp[n-2], dp[n-1]);}
};
算法的时间复杂度为O(n),遍历cost数组,并计算得到dp数组,空间复杂度同样为O(n),需要维护一个dp数组。
相关文章:

代码随想录算法训练营Day38|动态规划理论基础、2.斐波那契数、3.爬楼梯、4.使用最小花费爬楼梯
动态规划理论基础 代码随想录 (programmercarl.com) 动态规划(Dynamic Programming,简称DP)是一种算法设计技术,它通过将复杂问题分解为更小的子问题来解决优化问题。动态规划通常用于解决那些具有重叠子问题和最优子结构特性的…...

IIC通信总线
文章目录 1. IIC总线协议1. IIC简介2. IIC时序1. 数据有效性2. 起始信号和终止信号3. 数据格式4. 应答和非应答信号5. 时钟同步6. 写数据和读数据 2. AT24C023. AT24C02读写时序4. AT24C02配置步骤5. 代码部分1. IIC基本信号2. AT24C02驱动代码3. 实验结果分析 1. IIC总线协议 …...
2024 年最新 Python 调用 OpenAi 详细教程实现问答、图像合成、图像理解、语音合成、语音识别(详细教程)
OpenAi 环境安装 首先确保您的计算机上已经安装了 Python。您可以从 Python 官方网站下载并安装最新版本 Python。安装时,请确保勾选 “Add Python to PATH” (添加环境变量)选项,以便在 cmd 命令行中直接使用 Python。 安装 Op…...

git原理解释,windows 10 / ubuntu 24.04 安装使用 github
git的原理 git是赫赫有名的Linux之父Linus Torvalds从2005年起开发的文件版本管理系统,掌控Linux内核这样一个最为重量级的世界产品的Linus为什么要开发这个东西呢?因为Linux系统由全世界的程序员协作维护,对源代码文件的版本控制管理的需求…...
requests post json/data;requests response 接收不同数据
1、requests post json/data 在Python的requests库中,当你发送POST请求时,可以选择使用json参数或data参数来传递数据。这两者之间的主要区别在于它们如何被序列化和发送到服务器。 json参数: 当你使用json参数时,requests库会自…...
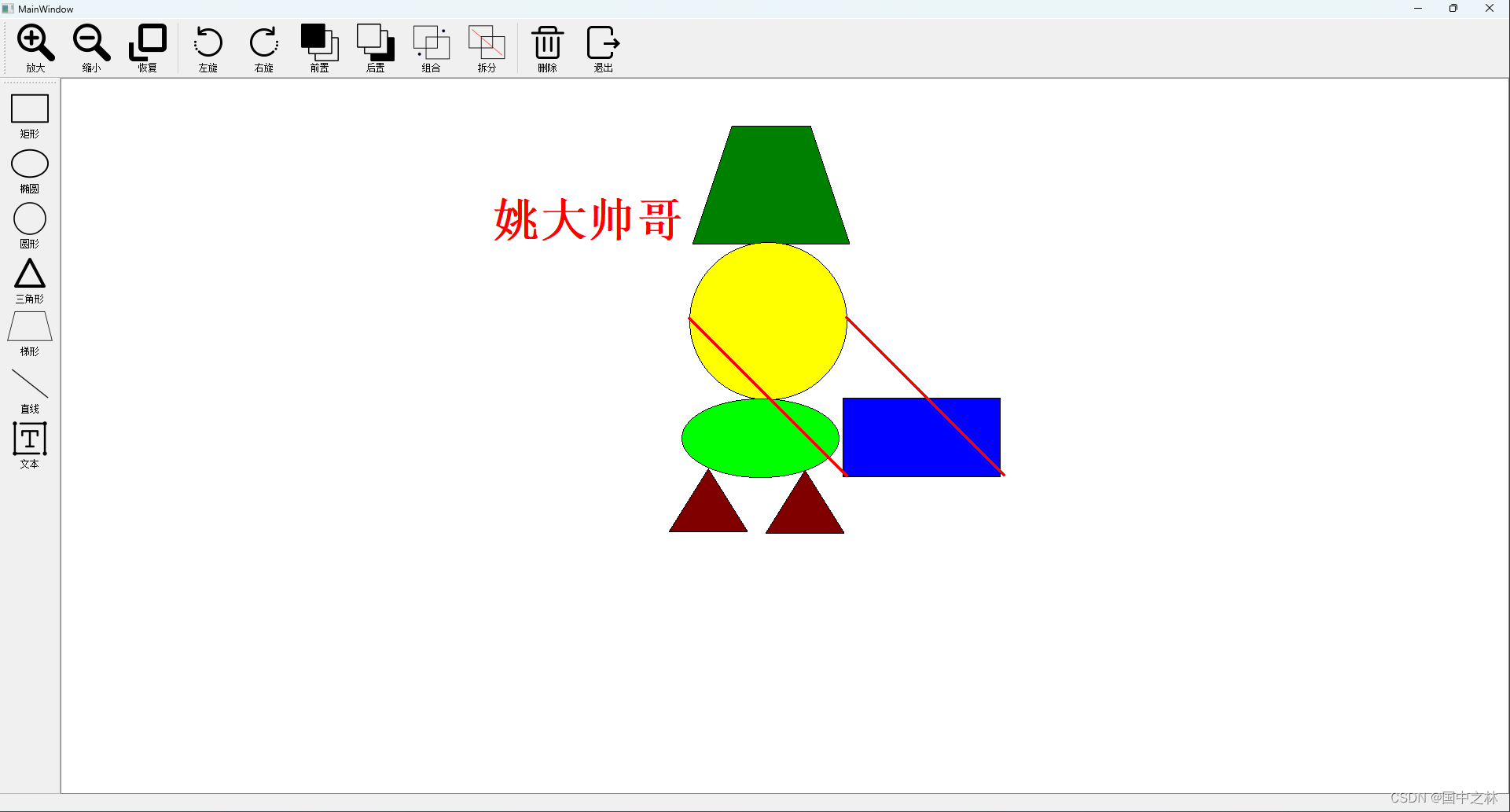
【qt】平面CAD(计算机辅助设计 )项目 上
CAD 一.前言二.界面设计三.提升类四.接受槽函数五.实现图形action1.矩形2.椭圆3.圆形4.三角形5.梯形6.直线7.文本 六.总结 一.前言 用我们上节课刚刚学过的GraphicsView架构来绘制一个可以交互的CAD项目! 效果图: 二.界面设计 添加2个工具栏 需要蔬菜的dd我! 添加action: …...

C++中bool类型的使用细节
C中bool类型的使用细节 ANSIISO C标准添加了一种名叫bool的新类型(对 C来说是新的)。它的名称来源于英国数学家 George Boole,是他开发了逻辑律的数学表示法。在计算中,布尔变量的值可以是true或false。过去,C和C一样,也没有布尔…...
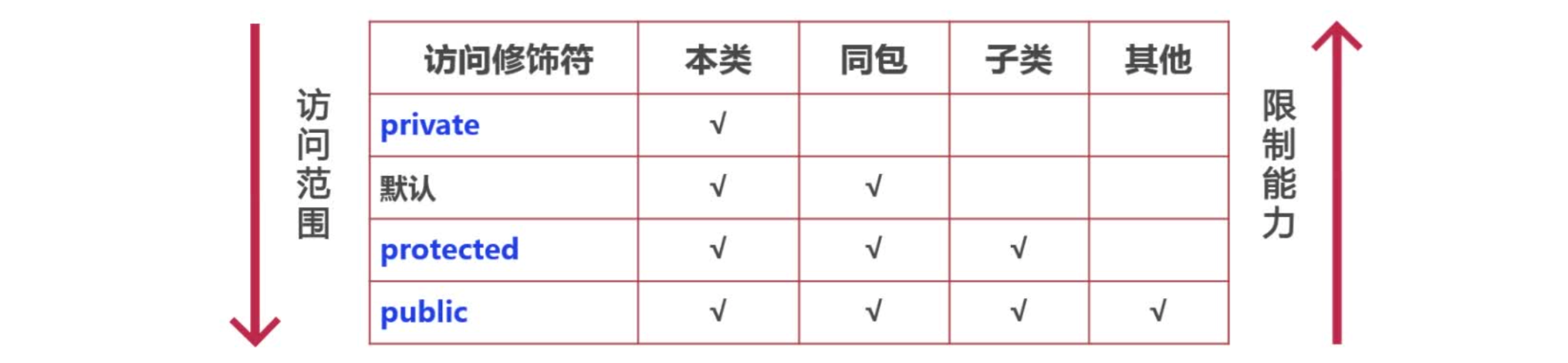
Java 面向对象 -- Java 语言的封装、继承、多态、内部类和 Object 类
大家好,我是栗筝i,这篇文章是我的 “栗筝i 的 Java 技术栈” 专栏的第 007 篇文章,在 “栗筝i 的 Java 技术栈” 这个专栏中我会持续为大家更新 Java 技术相关全套技术栈内容。专栏的主要目标是已经有一定 Java 开发经验,并希望进…...

【C++】和【预训练模型】实现【机器学习】【图像分类】的终极指南
目录 💗1. 准备工作和环境配置💕 💖安装OpenCV💕 💖安装Dlib💕 下载并编译TensorFlow C API💕 💗2. 下载和配置预训练模型💕 💖2.1 下载预训练的ResNet…...

HTML5 Web SQL数据库:浏览器中的轻量级数据库解决方案
在HTML5时代,Web开发迎来了一系列创新特性,其中之一便是Web SQL数据库。尽管Web SQL标准已被W3C废弃,转而推荐IndexedDB作为替代,但了解Web SQL对于学习Web存储技术的演进历程仍有其价值。本文将详细介绍Web SQL数据库的基本概念、…...

C++ const关键字有多种用法举例
C const关键字有多种用法 可以用来修饰变量、指针、函数参数、成员函数等。可以看到const在C中有多种用法,主要用于保证数据的不可变性,增强代码的安全性和可读性。在实际编程中,根据需要选择适当的const用法,可以有效避免意外修…...

Makefile-快速掌握
引用 本文完全参照大佬的文档写的,写这篇文章只是为了梳理一下知识 https://github.com/marmotedu/geekbang-go/blob/master/makefile/Makefile%E5%9F%BA%E7%A1%80%E7%9F%A5%E8%AF%86.md 介绍 Makefile是一个工程文件的编译规则,描述了整个工程的编译…...
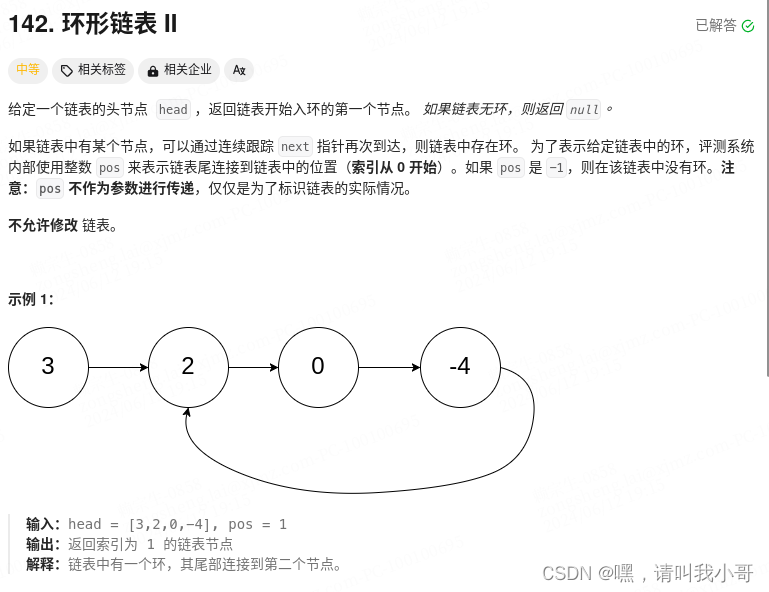
定个小目标之刷LeetCode热题(20)
这题与上一题有一点不同,上一题是判断链表是否存在环,这题是寻找入环的第一个节点,有一个规则是这样的,在存在环的情况下,运用快慢指针判断是否有环结束时,把快指针指向头结点,慢指针不变&#…...
短剧分销小程序:影视产业链中的新兴力量
一、引言 在数字化浪潮的推动下,影视产业正迎来一场深刻的变革。短剧分销小程序作为这场变革中的新兴力量,正以其独特的魅力和价值,逐渐在影视产业链中崭露头角。本文将探讨短剧分销小程序在影视产业链中的新兴地位、其带来的变革以及未来的…...

使用fvm切换flutter版本
切换flutter版本 下载fvm 1、dart pub global activate fvm dart下载fvm 2、warning中获取下载本地的地址 3、添加用户变量path: 下载地址 终端查看fvm版本 fvm --version 4、指定fvm文件缓存地址 fvm config --cache-path C:\src\fvm(自定义地址&…...
python通过selenium实现自动登录及轻松过滑块验证、点选验证码(2024-06-14)
一、chromedriver配置环境搭建 请确保下载的驱动程序与你的Chrome浏览器版本匹配,以确保正常运行。 1、Chrome版本号 chrome的地址栏输入chrome://version,自然就得到125.0.6422.142 版本 125.0.6422.142(正式版本) (…...

【C++】开源项目收集
C 是一种强大的、静态类型的通用编程语言,它的开源生态系统非常丰富,拥有众多高质量的项目。以下是一些知名的C开源项目: Boost: 这是一个庞大的库集合,提供了大量的实用工具和组件,如文件系统、网络编程、智能指针等&…...
爬虫相关面试题
一,如何抓取一个网站? 1,去百度和谷歌搜一下这个网站有没有分享要爬取数据的API 2, 看看电脑网页有没有所需要的数据,写代码测试调查好不好拿,如果好拿直接开始爬取 3,看看有没有电脑能打开的手机网页&a…...

Spring Cloud Netflix 之 Ribbon
前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家:https://www.captainbed.cn/z ChatGPT体验地址 文章目录 前言前言1、负载均衡1.1、服务端负载均衡1.2、客户端负载均衡 2、Ribbon实现服务…...

C语言怎样记住那么多的颜⾊?
一、问题 ⾚、橙、⻩、绿、⻘、蓝、紫,如此之多的颜⾊,数字不好记,英⽂看程序还可以, 直接写也不好写。那么怎样记住那么多的颜⾊呢? 二、解答 颜⾊枚举值如下: enum COLORS {BLACK, /*O⿊*/BLUE, …...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...
