Leetcode 3177. Find the Maximum Length of a Good Subsequence II
- Leetcode 3177. Find the Maximum Length of a Good Subsequence II
- 1. 解题思路
- 2. 代码实现
- 题目链接:3177. Find the Maximum Length of a Good Subsequence II
1. 解题思路
这一题我一开始的思路是直接使用暴力的动态规划的方式进行实现,结果遇到了内存爆炸的问题,后来看了一下别人的回答,整体的思路还是动态规划,但是存储结构上做了一些优化。
本质来说都是要做这么一个事:
if pre_num == nums[idx]:dp(idx, pre_num, k) = 1 + dp(idx+1, pre_num, k)
else:dp(idx, pre_num, k) = max(dp(idx+1, pre_num, k), 1 + dp(idx+1, nums[idx], k))
然后到具体实现上,如果直接这么实现无论是内存还是时间都扛不住,因此我们需要稍微做点优化,具体来说就是首先对pre_num进行一下cache,具体来说的话这里其实就是要分两种情况:
- 如果当前的数和前一个取值相同的情况
- 如果当前的数和前一个取值不同的情况
对于前者,我们不得不使用一个cache来存储所有可能的取值下的情况,对于后者,严格来说我们必须要找不同的情况,但是事实上我们可以偷个懒,直接取全部的情形,前者是后者的一个子集。
通过这种方式,就能够通过所有的测试样例……
2. 代码实现
给出python代码实现如下:
class Solution:def maximumLength(self, nums: List[int], k: int) -> int:n = len(nums)dp = [[0 for _ in range(k+1)] for _ in range(n)]same = [defaultdict(int) for _ in range(k+1)]diff = [0 for _ in range(k+1)]ans = 0for i, num in enumerate(nums):dp[i][0] = 1for j in range(k+1):dp[i][j] = 1 + same[j][num]if j > 0:dp[i][j] = max(dp[i][j], diff[j-1]+1)ans = max(ans, dp[i][j])for j in range(k+1):same[j][num] = max(same[j][num], dp[i][j])diff[j] = max(diff[j], dp[i][j])return ans
提交代码评测得到:耗时2052ms,占用内存29.4MB。
相关文章:

Leetcode 3177. Find the Maximum Length of a Good Subsequence II
Leetcode 3177. Find the Maximum Length of a Good Subsequence II 1. 解题思路2. 代码实现 题目链接:3177. Find the Maximum Length of a Good Subsequence II 1. 解题思路 这一题我一开始的思路是直接使用暴力的动态规划的方式进行实现,结果遇到了…...
)
程序员做电子书产品变现的复盘(2)
赚钱有多种,简单分为两类。 (1)手停口停型,这种工作在你积极从事时可能每天能带来数千甚至上万的收入,但一旦停止工作,收入就会大幅下降甚至归零,例如我们的日常工资。 (2…...

Java中的JVM是什么?如何调优JVM的性能?
Java中的JVM(Java Virtual Machine)是一个虚构出来的计算机,是一个规范,它在运行Java程序时扮演着核心角色。调优JVM的性能可以通过内存管理、垃圾回收、编译器优化等方法来提升Java应用程序的性能和稳定性。 Java中的JVM&#x…...

大型医院手术麻醉系统源码,前端采用Vue,Ant-Design开发,稳定成熟
医院手麻系统源码,手术麻醉信息系统,C#源码 医院手术麻醉信息系统包含了手术申请、排班、术前、术中、术后,直至出院的全过程。通过与相关医疗设备连接,与大屏幕显示公告相连接,实现了手术麻醉临床应用数据链全打通。…...
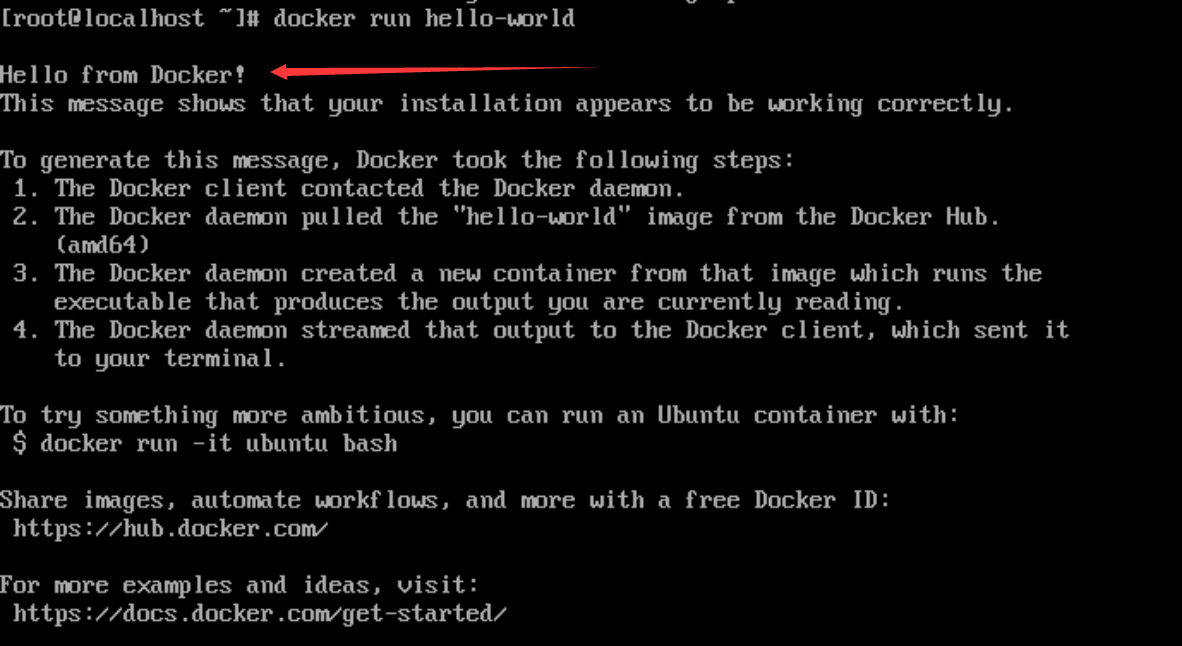
Linux安装Docker | 使用国内镜像
环境 CentOS7 先确认能够上网 curl www.baidu.com返回该输出说明网络OK 步骤一:安装gcc 和 gcc-c yum -y install gccyum -y install gcc-c步骤二:安装Docker仓库 yum install -y yum-utils接下来配置yum的国内镜像 yum-config-manager --add-re…...
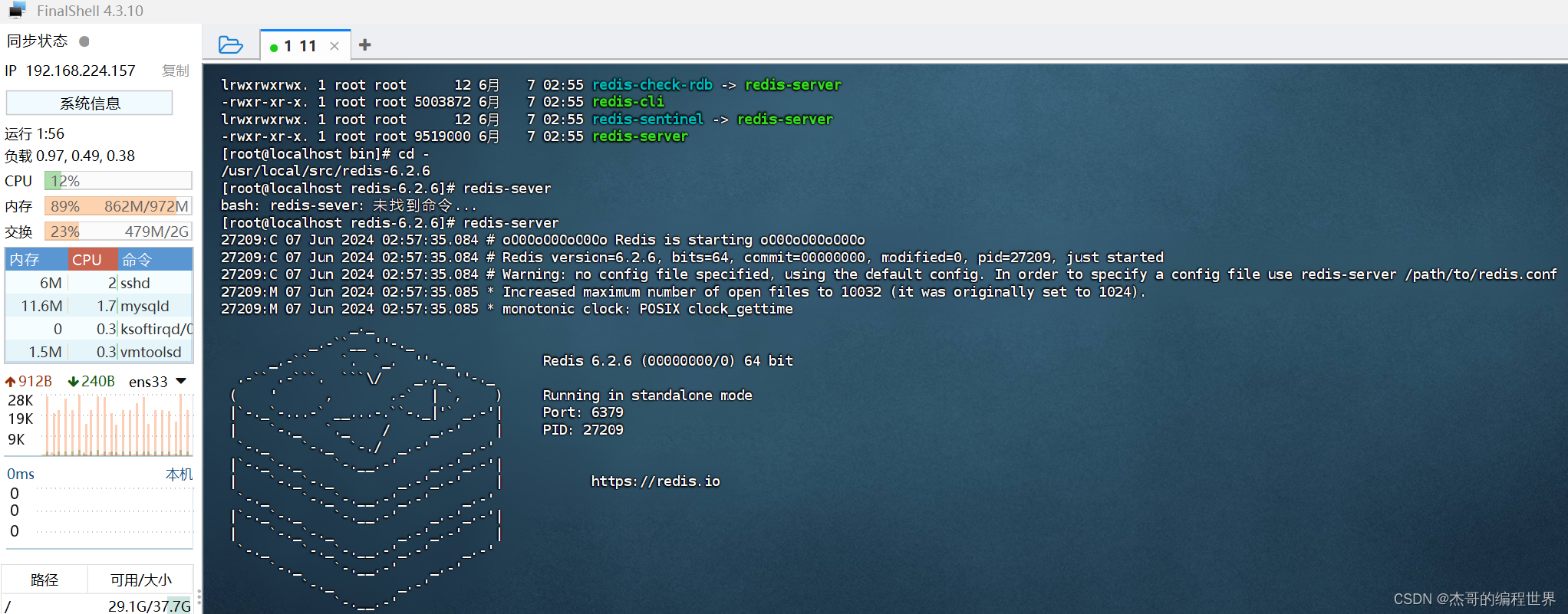
redis易懂快速安装(linux)2024
1.首先打开虚拟机系统 2.打开终端,输入su - 输入管理员密码,进入管理员用户 3.输入inconfig查看ip地址 4.打开final shell 连接虚拟机,输入ip和root用户以及密码 5.连接成功 6.输入 cd /usr/local/src/ 进入要安装的文件夹 6.点击上传按钮…...

关于数据库存储【\】转义字符反斜杠丢失的问题
背景 开始的时候,发现一个很奇怪的现象 富文本编辑器,前端存储带有"的内容,回显的时候解析就会出问题 后来发现,其实是只要是需要带有\进行转义的内容就会有问题 排查 从前端提交数据,后端获取数据ÿ…...

Unity3D 如何做好版本控制
目前项目这样版本控制: 1、在unity里,应该只对Assets(包含,meta)和ProjectSettings这两个文件夹做版本控制,其他的文件都是unity或工具生成出来的。 2、设置project setting ->editor setting-> Asset seriali…...
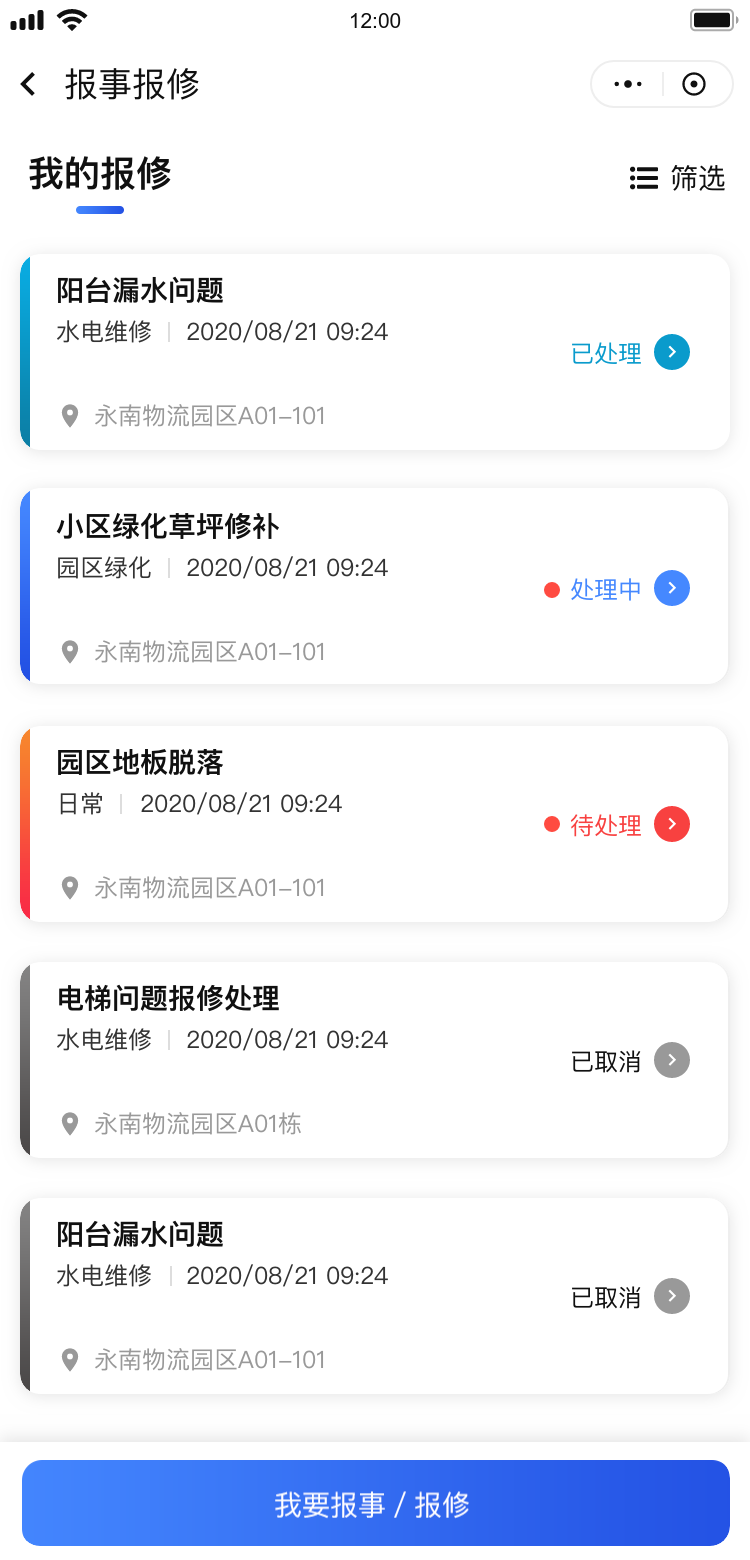
移动端消息中心,你未必会设计,发一些示例出来看看。
APP消息中心是一个用于管理和展示用户收到的各种消息和通知的功能模块。它在APP中的作用是提供一个集中管理和查看消息的界面,让用户能够方便地查看和处理各种消息。 以下是设计APP消息中心的一些建议: 1. 消息分类: 将消息按照不同的类型进…...

Non-zero exit code pycharm
目录 windows 设置conda代理: linux Conda 使用代理 4. 修改 Conda SSL 验证 pycharm 报错 exceted command pip 设置代理 Non-zero exit code 科学上网后,pip安装时警告报错 WARNING: Retrying (Retry(total0, connectNone, readNone, redirectNo…...
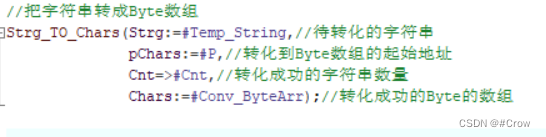
西门子学习笔记12 - BYTE-REAL互相转化
这是针对于前面MQTT协议的接收和发送数组只能是BYTE数组做出的对应的功能块封装。 1、BYTE-REAL转化 1、把byte数组转成字符串形式 2、把字符串转成浮点数 2、REAL-BYTE转化 1、把浮点数转成字符串 2、把字符串转成Byte数组...

科技云报道:“元年”之后,生成式AI将走向何方?
科技云报道原创。 近两年,以大模型为代表的生成式AI技术,成为引爆数字原生最重要的技术奇点,人们见证了各类文生应用的进展速度。Gartner预测,到2026年,超过80%的企业将使用生成式AI的API或模型,或在生产环…...

DAY02 HTML
这里写目录标题 一 WEB基础知识1. 我们可以做什么?2. WEB和Internet3. WEB 开发时需要用到的两类软件 二 HTML入门1. 前端涉及到的三个基础语言2. 定义3. HTML特点 三 HTML语法规则1. HTML 语法基础2. HTML网页结构3. HTML 网页注释 四 HTML标签1. 文本样式的标签2. 换行标签3…...
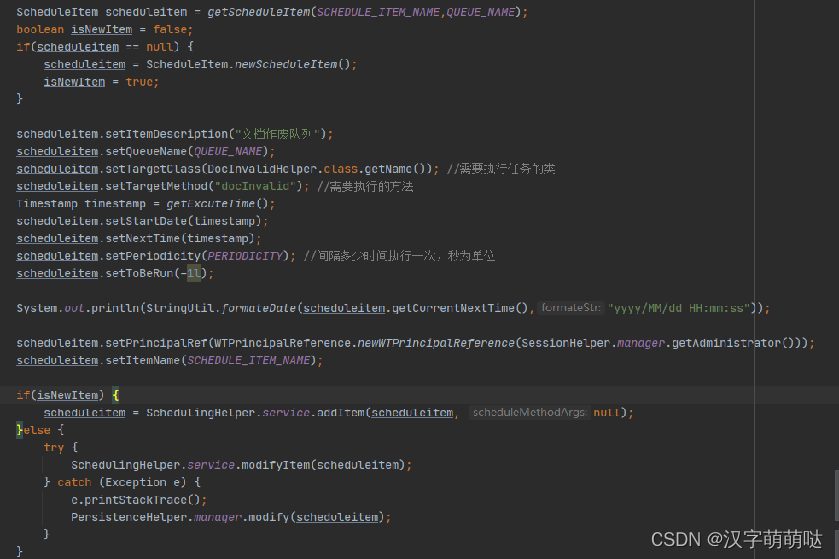
【Windchill监听器、队列、排程】
目录 Windchill监听器 监听器的概念 监听器的监听器实现原理 监听器的客制化 Windchill队列、排程 队列、排程的概念 Windchill常见出厂队列 自定义队列 Windchill 11新增功能 Windchill监听器 监听器的概念 监听器,字面上的理解就是监听观察某个事件&…...

统计信号处理基础 习题解答10-14
题目: 观测到数据 其中是已知的,是方差为的WGN,且和独立,求的MMSE估计量以及最小贝叶斯MSE。 解答: 观测到的数据写成矢量形式: 其中: 根据题目条件,符合定理10.3,因此…...

APP各种抓包教程
APP各种抓包教程 9/100 发布文章 wananxuexihu 未选择任何文件 new 前言 每当遇到一些 APP 渗透测试项目的时候,抓不了包的问题令人有点难受,但是抓不了包并不能代表目标系统很安全,那么接下来我会整理一下目前我所了解到的一些抓包方法 **声…...

web前端开发项目教学:深入剖析四大核心、五大技能、六大实战、七大建议
web前端开发项目教学:深入剖析四大核心、五大技能、六大实战、七大建议 在数字化的今天,Web前端开发已成为一项不可或缺的技能。无论是初学者还是有一定经验的开发者,都需要通过系统的项目教学来提升自己的技能水平。本文将围绕Web前端开发项…...

从入门到高手的99个python案例(2)
51. 列表和数组比较 - 列表通用,NumPy数组高效。 import numpy as np normal_list [1, 2, 3] np_array np.array([1, 2, 3]) print(np_array.shape) # 输出 (3,), 数组有形状信息 52. Python的内置模块datetime - 处理日期和时间。 from datetime import…...
)
btstack协议栈实战篇--Performance - Stream Data over SPP (Server)
btstack协议栈---总目录_bt stack是什么-CSDN博客 目录 1.Track throughput 2.Packet Handler 3.btstack_main 4.log信息 RFCOMM连接打开后,请求RFCOMM EVENT CAN SEND NOW,通过rfcomm request can send now event()。 当我们得到RFCOMM EVENT CAN SEND NOW…...

ThinkPHP5.0 apache服务器配置URL重写,index.php去除
本地环境wamp .htaccess文件代码 <IfModule mod_rewrite.c>Options FollowSymlinks -MultiviewsRewriteEngine onRewriteCond %{REQUEST_FILENAME} !-dRewriteCond %{REQUEST_FILENAME} !-fRewriteRule ^(.*)$ index.php?/$1 [QSA,PT,L] </IfModule> 踩过这个坑&a…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...
