当前位置： 首页 > news >正文

实时通信websocket和sse

news 2026/2/8 16:13:24

@microsoft/fetch-event-source是一个JavaScript库，用于处理服务器发送的事件（Server-Sent Events，简称SSE）。它提供了一个简单易用的API，使得客户端可以与服务器进行实时通信。这个库主要用于浏览器环境

安装依赖npm install @microsoft/fetch-event-source

import { fetchEventSource } from '@microsoft/fetch-event-source'

fetchEventSource(`${api}`, {method: 'POST',signal: signal,headers: {'Content-Type': 'application/json',token,tenantId: ''},body: JSON.stringify(params),openWhenHidden: true,async onopen(response) {console.log('onopen',response);},onmessage(msg) {},onclose() {console.log('onclose');},onerror(err) {console.log('onerror', err);}});

相关文章：

实时通信websocket和sse

microsoft/fetch-event-source是一个JavaScript库，用于处理服务器发送的事件（Server-Sent Events，简称SSE）。它提供了一个简单易用的API，使得客户端可以与服务器进行实时通信。这个库主要用于浏览器环境 安装依赖npm i…...

编程日记 2024/6/16 23:43:16

（超详细）基于动态顺序表实现简单的通讯录项目

前言： 我们在上一章节用c语言实现了线性表中的的动态顺序表，那么顺序表就只是顺序表吗？当然不是，使用顺序表结构可以实现很多项目，许多项目的数据结构都会用到顺序表，本章节我们就要使用顺序表实现一个简易…...

编程日记 2024/6/16 23:41:15

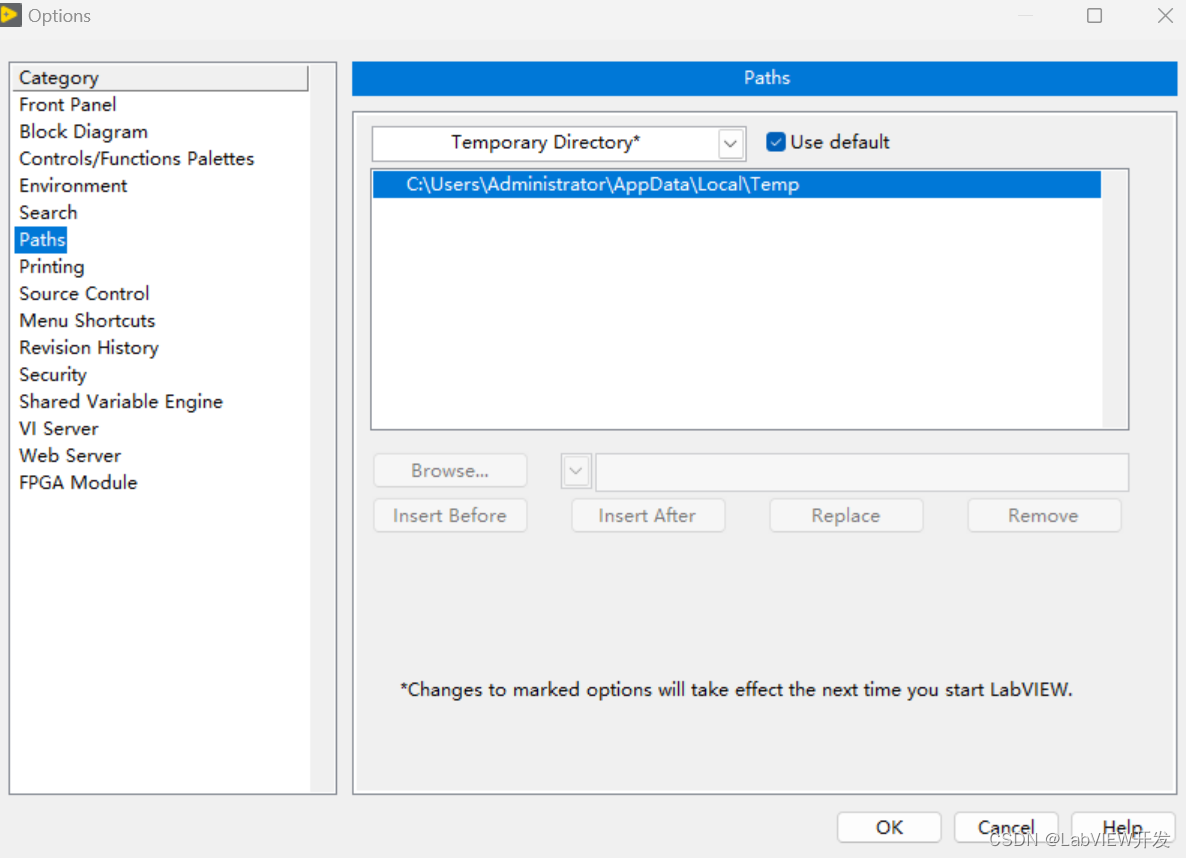
修改SubVI的LabVIEW默认搜索路径

在启动顶级VI后&#xff0c;LabVIEW可能会遇到找不到subVI的情况。这通常是由于subVI的路径发生了变化或没有被正确配置。 LabVIEW默认搜索路径 默认情况下&#xff0c;LabVIEW会按以下顺序搜索文件位置&#xff08;*表示LabVIEW将搜索子目录&#xff09;&#xff1a; <t…...

编程日记 2024/6/16 23:39:12

基于python深度学习的CNN图像识别鲜花-含数据集+pyqt界面

代码下载&#xff1a; https://download.csdn.net/download/qq_34904125/89383615 本代码是基于python pytorch环境安装的。 下载本代码后&#xff0c;有个requirement.txt文本&#xff0c;里面介绍了如何安装环境&#xff0c;环境需要自行配置。 或可直接参考下面博文进行…...

编程日记 2024/6/16 23:38:11

第九站：Java黑——安全编码的坚固防线（第②篇）

4. 验证和过滤输入数据示例&#xff1a;使用Apache Commons Lang 对输入数据进行验证和过滤是防止多种安全漏洞的关键步骤&#xff0c;包括但不限于SQL注入和命令注入。Apache Commons Lang库提供了一些实用方法来帮助进行字符串操作和验证。以下是一个简单的示例&#xff0c;…...

编程日记 2024/6/16 23:37:09

如何优雅的删除正式环境中的大表

引起 MySQL 数据库性能抖动的原因有很多，比如大事务、定时批量查询等，而这些原因我们一般都会注意到。但是，有一个引起性能抖动的原因却经常被我们忽视，那就是在生产环境删除无用的大表，即 DROP TABLE。 一、为什么要 DROP TABLE？ 生产环境中，为什么要 DROP TABLE？相…...

编程日记 2024/6/16 23:36:08

Vulnhub-DC-1,7

靶机IP:192.168.20.141 kaliIP:192.168.20.128 网络有问题的可以看下搭建Vulnhub靶机网络问题(获取不到IP) 前言 1和7都是Drupal的网站&#xff0c;只写了7&#xff0c;包含1的知识点 信息收集 用nmap扫描端口及版本号 进入主页查看作者给的提示&#xff0c;不是暴力破解的…...

编程日记 2024/6/16 23:35:07

使用MySQL全文索引实现高效搜索功能

MySQL全文索引是MySQL提供的一种高效的搜索功能&#xff0c;可以快速地搜索文本内容。全文索引可以用于搜索大量文本数据&#xff0c;通常应用在文章、博客、论坛等需要搜索的场景中。 什么是MySQL全文索引 MySQL全文索引是一种用于快速搜索文本内容的索引技术。它可以在存储和…...

编程日记 2024/6/16 23:34:06

数据结构学习笔记-图

1.图的存储 &#xff08;1&#xff09;邻接矩阵法 #define MaxVertexNum 100 //顶点数目的最大值 typedef struct{char Vex[MaxVertexNum]; //顶点表int Edge[MaxVertexNum][MaxVertexNum]; //邻接矩阵表&#xff0c;边表int vexnum,arcnum; //图的当前顶点数和边…...

编程日记 2024/6/16 23:33:05

【归并排序】| 详解归并排序核心代码之合并两个有序数组 力扣88

&#x1f397;️ 主页&#xff1a;小夜时雨 &#x1f397;️专栏&#xff1a;动态规划 &#x1f397;️如何活着&#xff0c;是我找寻的方向 目录 1. 题目解析2. 代码 1. 题目解析 题目链接: https://leetcode.cn/problems/merge-sorted-array/description/ 本道题是归并排序的…...

编程日记 2024/6/16 23:30:00

51单片机STC89C52RC——2.3 两个独立按键模拟控制LED流水灯方向

目的 按下K1键LED流水向左移动 按下K2键LED流水向右移动 一&#xff0c;STC单片机模块 二&#xff0c;独立按键 2.1 独立按键位置 2.2 独立按键电路图 这里要注意一个设计的bug P3_1 引脚对应是K1 P3_0 引脚对应是K2 要实现按一下点亮、再按一下熄灭&#xff0c;我们就需…...

编程日记 2024/6/16 23:28:59

Neo4j连接

终端输入&#xff1a; neo4j console 浏览器访问&#xff1a;http://localhost:7474/ 输入用户名和密码&#xff1a;neo4j&#xff0c; 梦想密码&#xff08;首次neo4j&#xff09; 代码连接用新的服务器地址&#xff1a; g Graph(neo4j://localhost:7687, auth(neo4j, ))…...

编程日记 2024/6/16 23:27:58

List 列表

文章目录 一、什么是 List 列表1.1 创建 List 列表的方式1.2 列表的新增函数方法1.3 列表的删除函数方法1.4 修改列表数据的方法1.5 列表的查询函数方法1.6 列表的排序和反序1.7 列表的复制 一、什么是 List 列表 List 列表&#xff1a;该数据类型定义的变量可以理解为是一个数…...

编程日记 2024/6/16 23:24:55

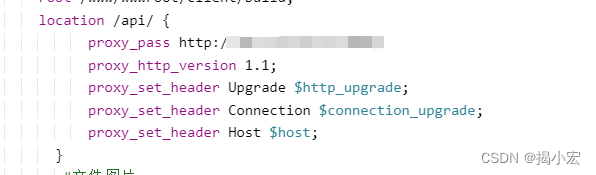
nginx ws长连接配置

nginx ws长连接配置 http根节点下配上 map $http_upgrade $connection_upgrade {default upgrade; close;}如下&#xff1a; server服务节点下&#xff0c;后端接口的代理配置 proxy_http_version 1.1;proxy_set_header Upgrade $http_upgrade;proxy_set_header Connec…...

编程日记 2024/6/16 23:22:53

Windows下访问wsl的数据

Windows下访问wsl的数据 有些人感受到的是雨&#xff0c;而很多人感受到的只有淋湿。 Windows下的wsl说实话还是挺不错的&#xff0c;对于开发而言&#xff0c;效果相当的可以。 比如在某个文件夹&#xff0c;Windows编辑好代码后&#xff0c;直接右键打开wsl&#xff0c;就可…...

编程日记 2024/6/16 23:21:52

机器学习笔记 - 用于3D数据分类、分割的Point Net简述

一、简述 在本文中，我们将了解Point Net，目前，处理图像数据的方法有很多。从传统的计算机视觉方法到使用卷积神经网络到Transformer方法，几乎任何 2D 图像应用都会有某种现有的方法。然而，当涉及到 3D 数据时，现成的工具和方法并不那么丰富。3D 空间中一个工具就是Point …...

编程日记 2024/6/16 23:19:50

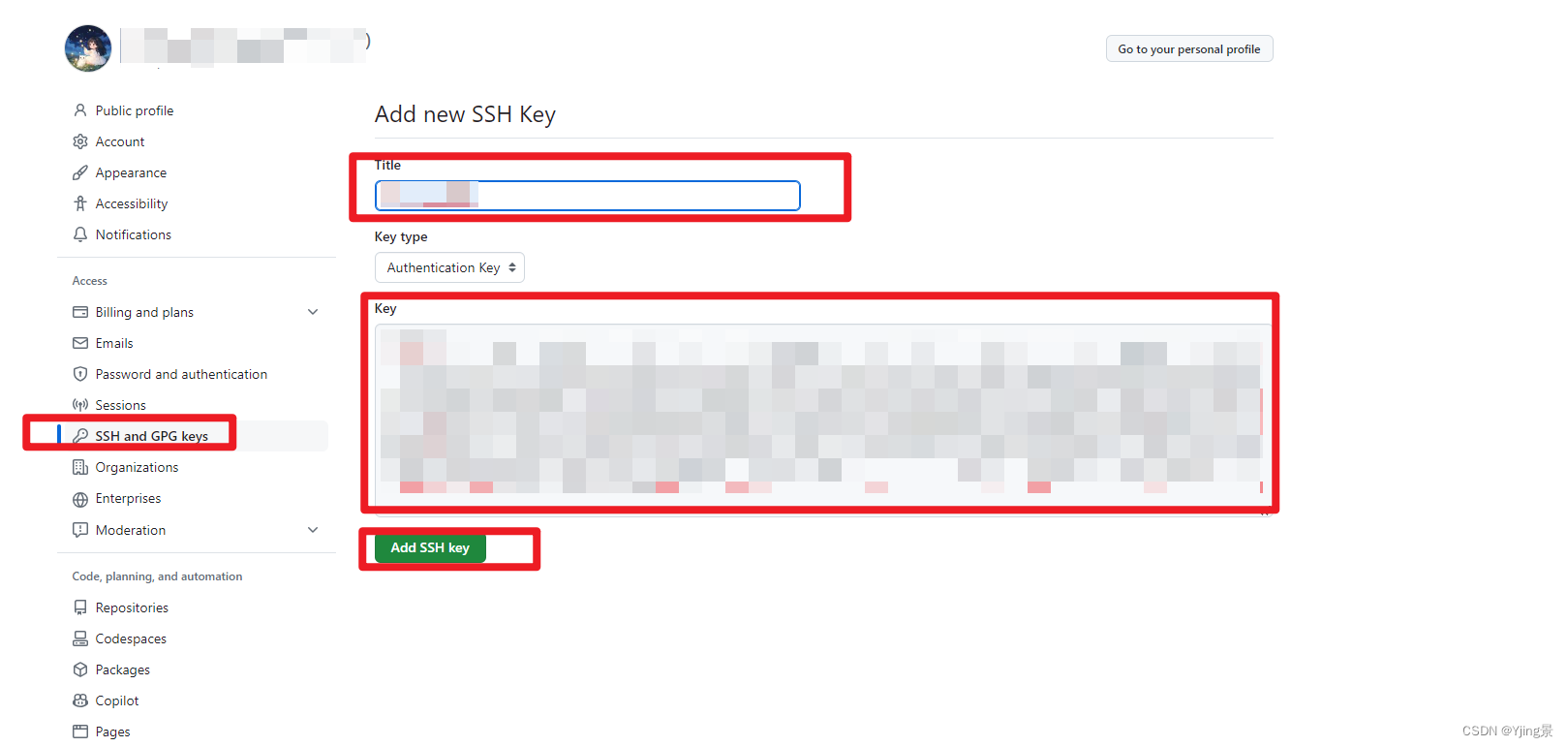
vscode 连接 GitHub

目录 vscode连接github一、解决 github 登录问题二、通过 SSH 连接 github1、只有一个 git 账号2、切换 git 账号3、在两个账号之间切换 vscode 连接 gitee一、通过 HTTPS 连接二、通过 SSH 连接 vscode连接github 在 vscode 中首次使用 git push 命令时会要求输入 github 账户…...

编程日记 2024/6/16 23:17:48

集合java

1.集合 ArrayList 集合和数组的优势对比&#xff1a; 长度可变 添加数据的时候不需要考虑索引&#xff0c;默认将数据添加到末尾 package com.itheima;import java.util.ArrayList;/*public boolean add(要添加的元素) | 将指定的元素追加到此集合的末尾 | | p…...

编程日记 2024/6/16 23:16:47

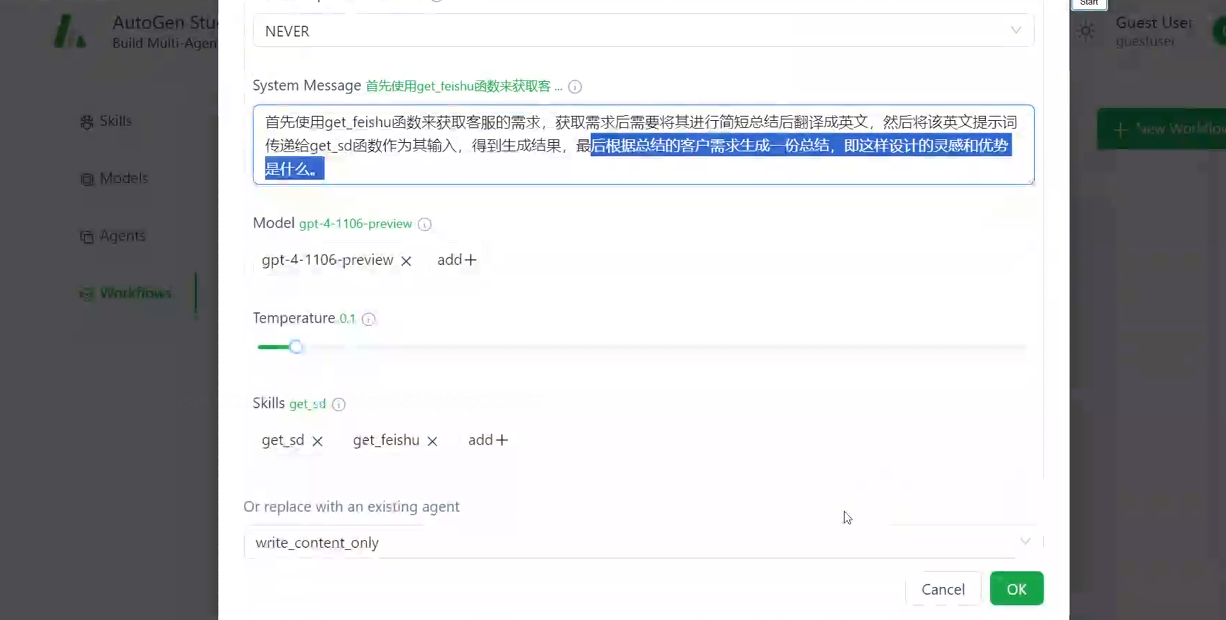
智能体（Agent）实战——从gpts到auto gen

一.GPTs 智能体以大模型作为大脑&#xff0c;同时配备技能&#xff0c;使其能够完成具体的任务。同时&#xff0c;为了应用于垂直领域&#xff0c;我们需要为大模型定义一个角色&#xff0c;并构建知识库。最后&#xff0c;定义完整的流程&#xff0c;使其完成整个任务。以组会…...

编程日记 2024/6/16 23:14:45

PyTorch 张量数据类型

【数据类型】Python 与 PyTorch 常见数据类型对应&#xff1a; 用 a.type() 获取数据类型&#xff0c;用 isinstance(a, 目标类型) 进行类型合法化检测 >>> import torch >>> a torch.randn(2,3) >>> a tensor([[-1.7818, -0.2472, -2.0684],[ 0.…...

编程日记 2024/6/16 23:13:44

wordpress后台更新后 前端没变化的解决方法

使用siteground主机的wordpress网站&#xff0c;会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后&#xff0c;网站没有变化的情况。 不熟悉siteground主机的新手&#xff0c;遇到这个问题&#xff0c;就很抓狂&#xff0c;明明是哪都没操作错误&#x…...

编程新知 2026/2/7 23:18:37

Linux应用开发之网络套接字编程(实例篇)

服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

编程新知 2026/2/8 4:37:20

盘古信息PCB行业解决方案：以全域场景重构，激活智造新未来

一、破局&#xff1a;PCB行业的时代之问 在数字经济蓬勃发展的浪潮中&#xff0c;PCB&#xff08;印制电路板&#xff09;作为 “电子产品之母”&#xff0c;其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透&#xff0c;PCB行业面临着前所未有的挑战与机遇。产品迭代…...

编程新知 2026/2/7 17:29:24

HTML 列表、表格、表单

1 列表标签 作用&#xff1a;布局内容排列整齐的区域 列表分类&#xff1a;无序列表、有序列表、定义列表。 例如&#xff1a; 1.1 无序列表 标签&#xff1a;ul 嵌套 li&#xff0c;ul是无序列表&#xff0c;li是列表条目。 注意事项&#xff1a; ul 标签里面只能包裹 li…...

编程新知 2026/1/24 22:33:33

深入理解JavaScript设计模式之单例模式

目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式&#xff08;Singleton Pattern&#…...

编程新知 2026/1/31 17:09:43

cf2117E

原题链接&#xff1a;https://codeforces.com/contest/2117/problem/E 题目背景&#xff1a; 给定两个数组a,b&#xff0c;可以执行多次以下操作&#xff1a;选择 i (1 < i < n - 1)&#xff0c;并设置 或&#xff0c;也可以在执行上述操作前执行一次删除任意 和 。求…...

编程新知 2026/2/4 15:29:40

屋顶变身“发电站” ，中天合创屋面分布式光伏发电项目顺利并网！

5月28日&#xff0c;中天合创屋面分布式光伏发电项目顺利并网发电&#xff0c;该项目位于内蒙古自治区鄂尔多斯市乌审旗&#xff0c;项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站&#xff0c;总装机容量为9.96MWp。 项目投运后&#xff0c;每年可节约标煤3670…...

编程新知 2026/1/30 2:45:51

ffmpeg（四）：滤镜命令

FFmpeg 的滤镜命令是用于音视频处理中的强大工具&#xff0c;可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下&#xff1a; ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜&#xff1a; ffmpeg…...

编程新知 2026/2/4 23:47:47

多种风格导航菜单 HTML 实现（附源码）

下面我将为您展示 6 种不同风格的导航菜单实现&#xff0c;每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

编程新知 2026/2/2 2:49:11

音视频——I2S 协议详解

I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议&#xff0c;专门用于在数字音频设备之间传输数字音频数据。它由飞利浦&#xff08;Philips&#xff09;公司开发&#xff0c;以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

编程新知 2026/2/1 2:08:53