【机器学习】第7章 集成学习(小重点,混之前章节出题但小题)
一、概念
1.集成学习,顾名思义,不是一个玩意,而是一堆玩意混合到一块。
(1)基本思想是先 生成一定数量基学习器,再采用集成策略 将这堆基学习器的预测结果组合起来,从而形成最终结论。
(2)一般而言,基学习器可以是同质的“弱学习器”,也可以是异质的“弱学习器”。 (3)目前,同质基学习器应用最广泛,其使用最多的模型是CART决策树和神经网络。
2.生成基学习器
同质个体学习器按照个体学习器之间是否存在依赖关系又可以分为两类:
(1)存在着强依赖关系,串行生成个体学习器。
原理是利用依赖关系,对之前训练中错误标记的样本赋以较高的权重值,以提高整体的预测效果。
代表算法是Boosting算法。
(2)不存在强依赖关系,并行生成这些个体学习器。
并行的原理是利用基学习器之间的独立性,通过平均可以显著降低错误率。
代表算法是Bagging和随机森林(Random Forest)算法。
3.集成策略
根据集成学习的用途不同,结论合成的方法也各不相同。
(1)通常是由各个体学习器的输出投票产生。
通常采用绝对多数投票法或相对多数投票法。
(2)当用于回归估计时,一般由各学习器的输出通过 简单平均或加权平均产生。
4.Bagging
(1)思路是从原始样本集合中采样,得到若干个大小相同的样本集,然后在每个样本集合上分别训练一个模型,最后用投票法进行预测。
(2)采样方式:用于训练的每个模型的样本集合Dt是从D中有放回采样得到的
(3)训练得到的模型可用于分类也可用于回归:
分类:投票法
回归:加权平均法
5.随机森林
说白了就是建了一堆简单版的决策树,然后放一块变成森林模拟器,这个健壮性一下就上来了。
(1)抽样产生每棵决策树的训练数据集。
随机森林从原始训练数据集中产生n个训练子集(假设要随机生成n棵决策树)。
训练子集中的样本存在一定的重复,主要是为了在训练模型时,每一棵树的输入样本都不是全部的样本,使森林中的决策树不至于产生局部最优解。
(2)构建n棵决策树(基学习器)。
每棵决策树不需要剪枝处理。由于随机森林在进行结点分裂时,随机地选择m个特征参与比较,而不是像决策树将所有特征都参与特征指标的计算。这样减少了决策树之间的相关性,提升了决策树的分类精度,从而达到结点的随机性。
(3)生成随机森林。使用第(2)步n棵决策树对测试样本进行分类,随机森林将每棵子树的结果汇总,以少数服从多数的原则决定该样本的类别。
6. Boosting
(1)是一种可将弱学习器提升为强学习器的算法。
这种算法先从初始训练集训练出一个基学习器,再根据基学习器的表现对训练样本分布进行调整,使得先前基学习器做错的训练样本在后续受到更多关注,然后基于调整后的样本分布来训练下一个基学习器。
(2)如此重复进行,直至基学习器数目达到事先指定的值T,最终将这T个基学习器进行加权结合。
(3)分好几种,如AdaBoost,GradientBoosting,LogitBoost等,其中最著名的代表是AdaBoost算法。Boosting中的个体分类器可以是不同类的分类器。
7.偏差与方差(重点)
(1)偏差bias
偏差是指预测结果与真实值之间的差异,排除噪声的影响,偏差更多的是针对某个模型输出的样本误差。
偏差是模型无法准确表达数据关系导致,比如模型过于简单,非线性的数据关系采用线性模型建模,偏差较大的模型是错的模型。
(2)方差variance
模型方差不是针对某一个模型输出样本进行判定,而是指多个(次)模型输出的结果之间的离散差异(注意这里写的是多个(次)模型,即 不同模型 或 同一模型不同时间 的输出结果方差较大)。
方差是由训练集的数据不够导致。
一方面量 (数据量) 不够,有限的数据集过度训练导致模型复杂,另一方面质(样本质量)不行,测试集中的数据分布未在训练集中,导致每次抽样训练模型时,每次模型参数不同,导致无法准确的预测出正确结果。
(3)偏差决定中心点(期望输出与真实标记的差别),方差决定分布(使用样本数相同的不同训练集产生的方差):
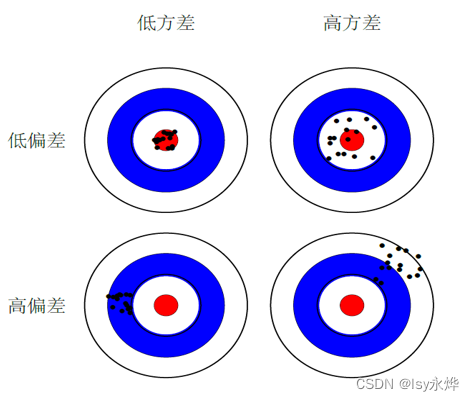
(4)泛化误差可以分解为偏差(Biase)、方差(Variance)和噪声(Noise)
8.如何解决偏差、方差问题
首先,要知道偏差和方差是无法完全避免的,只能尽量减少其影响。
(1)偏差:实际上也可以称为避免欠拟合。
1.寻找更好的特征 -- 具有代表性。
2.更多的特征 -- 增大输入向量的维度,增加模型复杂度。
(2)方差:实际上也可以称为避免过拟合 。
1.增大数据集合 -- 使用更多的数据,减少数据扰动所造成的影响
2.减少数据特征 -- 减少数据维度,减少模型复杂度
3.正则化方法
4.交叉验证法
二、习题
单选题
11. 集成学习的主要思想是(B)。
A、将多源数据进行融合学习
B、将多个机器学习模型组合起来解决问题
C、将多个数据集合集成在一起进行训练
D、通过聚类算法使数据集分为多个簇
12. 下列不是Bagging算法特点的是(D)。
A、各基分类器不存在强依赖关系,并行生成基分类器
B、各基分类器权重相同,训练出来的每个模型独立同分布
C、通过有放回采样获取每个模型的样本集合
D、只需要较少的基分类器
Bagging算法通常会生成多个基分类器,而不是较少的。增加基分类器的数量可以提高整体模型的泛化能力和稳定性。
13. 下列关于随机森林的说法错误的是(B)。
A、易于实现、易于并行。
B、基本单元是决策树,将所有特征都参与特征指标的计算。
C、通过集成学习的思想将多棵树集成的一种算法。
D、在引入样本扰动的基础上,又引入了属性扰动。
在随机森林中,并不是所有特征都会参与到每棵树的建立中。随机森林在每棵树的建立过程中会随机选择一部分特征进行训练,这个过程被称为特征子集采样。
14. 下列哪个集成学习器的个体学习器存在强依赖关系(A)
A、Boosting
B、Bagging
C、EM
D、Random Forest
15. 下列哪个不是Boosting 的特点(D)
A、基分类器彼此关联
B、串行训练算法
C、通过不断减小分类器的训练偏差将弱学习器提升为强学习器
D、Boosting中的基分类器只能是不同类的分类器
16. 模型的方差(B),说明模型在不同采样分布下,泛化能力大致相当;
模型的偏差(),说明模型对样本的预测越准,模型的拟合性越好。
A、越小 越大
B、越小 越小
C、越大 越小
D、越大 越大
17. 在集成学习两大类策略中,boosting和bagging如何影响模型的偏差(bias)和方差(variance)( C )。
A、boosting和bagging均使得方差减小
B、boosting和bagging均使得偏差减小
C、boosting使得偏差减小,bagging使得方差减小
D、boosting使得方差减小,bagging使得偏差减小
boosting是打一个样本集不断优化的战斗对应偏差是样本偏差,bagging是玩一堆方法去养蛊对应方差针对“多”这个特点。
判断题
14. 低方差的优化结果比高方差的优化结果更集中( P)
15. 模型的方差和偏差之和越大,模型性能的误差越小,泛化能力越强(Í )
不论是偏差还是方差都是越小越好
相关文章:

【机器学习】第7章 集成学习(小重点,混之前章节出题但小题)
一、概念 1.集成学习,顾名思义,不是一个玩意,而是一堆玩意混合到一块。 (1)基本思想是先 生成一定数量基学习器,再采用集成策略 将这堆基学习器的预测结果组合起来,从而形成最终结论。 &#x…...

代码随想录——子集Ⅱ(Leecode 90)
题目链接 回溯 class Solution {List<List<Integer>> res new ArrayList<List<Integer>>();List<Integer> list new ArrayList<Integer>();boolean[] used; public List<List<Integer>> subsetsWithDup(int[] nums) {use…...
)
vue关闭页面时触发的函数(ai生成)
在Vue中,可以通过监听浏览器的beforeunload事件来在关闭页面前触发函数。这里是一个简单的示例: new Vue({el: #app,methods: {handleBeforeUnload(event) {// 设置returnValue属性以显示确认对话框event.returnValue 你确定要离开吗?;// 在…...

马尔可夫性质与Q学习在强化学习中的结合
马尔可夫性质是强化学习(RL)算法的基础,特别是在Q学习中。马尔可夫性质指出,系统的未来状态只依赖于当前状态,而与之前的状态序列无关。这一性质简化了学习最优策略的问题,因为它减少了状态转移的复杂性。 …...

【LeetCode 5.】 最长回文子串
一道题能否使用动态规划就在于判断最优结构是否是通过最优子结构推导得到?如果显然具备这个特性,那么就应该朝动态规划思考。如果令dp[i][j]表示串s[i:j1]是否是回文子串,那么判断dp[i][j] 是否是回文子串,相当于判断s[i] 与 s[j]…...

联邦学习周记|第四周
论文:Active Federated Learning 链接 将主动学习引入FL,每次随机抽几个Client拿来train,把置信值低的Client概率调大,就能少跑几次。 论文:Active learning based federated learning for waste and natural disast…...
机器学习课程复习——逻辑回归
1. 激活函数 Q:激活函数有哪些? SigmoidS型函数Tanh 双曲正切函数...
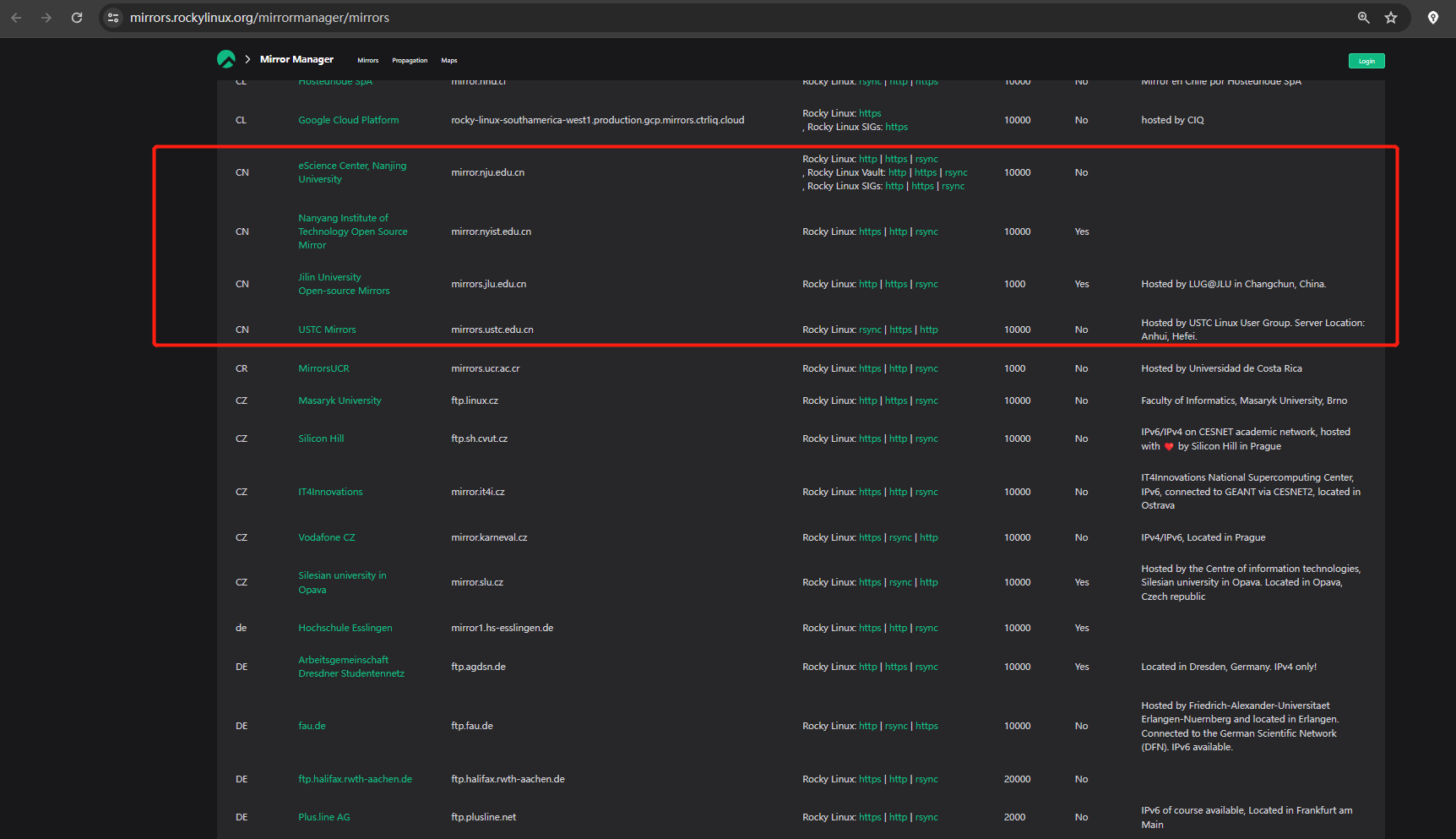
Rocky Linux 更换CN镜像地址
官方镜像列表,下拉查找 官方镜像列表:https://mirrors.rockylinux.org/mirrormanager/mirrorsCN 开头的站点。 一键更改镜像地址脚本 以下是更改从默认更改到阿里云地址 cat <<EOF>>/RackyLinux_Update_repo.sh #!/bin/bash # -*- codin…...

Linux rm命令由于要删的文件太多报-bash: /usr/bin/rm:参数列表过长,无法删除的解决办法
银河麒麟系统,在使用rm命令删除文件时报了如下错误,删不掉: 查了一下,原因就是要删除的文件太多了,例如我当前要删的文件共有这么多: 查到了解决办法,记录在此。需要使用xargs命令来解决参数列表…...
【包管理】Node.JS与Ptyhon安装
文章目录 Node.JSPtyhon Node.JS Node.js的安装通常包括以下几个步骤: 访问Node.js官网: 打开Node.js的官方网站(如:https://nodejs.org/zh-cn/download/)。 下载安装包: 根据你的操作系统选择对应的Node…...

SpringMVC系列四: Rest-优雅的url请求风格
Rest请求 💞Rest基本介绍💞Rest风格的url-完成增删改查需求说明代码实现HiddenHttpMethodFilter机制注意事项和细节 💞课后作业 上一讲, 我们学习的是SpringMVC系列三: Postman(接口测试工具) 现在打开springmvc项目 💞Rest基本介…...

Hexo 搭建个人博客(ubuntu20.04)
1 安装 Nodejs 和 npm 首先登录NodeSource官网: Nodesource Node.js DEB 按照提示安装最新的 Node.js 及其配套版本的 npm。 (1)以 sudo 用户身份运行下面的命令,下载并执行 NodeSource 安装脚本: sudo curl -fsSL…...

【论文阅读】-- Attribute-Aware RBFs:使用 RT Core 范围查询交互式可视化时间序列颗粒体积
Attribute-Aware RBFs: Interactive Visualization of Time Series Particle Volumes Using RT Core Range Queries 摘要1 引言2 相关工作2.1 粒子体渲染2.2 RT核心方法 3 渲染彩色时间序列粒子体积3.1 场重构3.1.1 密度场 Φ3.1.2 属性字段 θ3.1.3 优化场重建 3.2 树结构构建…...

A类IP介绍
1)A类ip给谁用: 给广域网用,公网ip使用A类地址,作为公网ip时,Ip地址是全球唯一的。 2)基本介绍 ip地址范围 - 理论范围 0.0.0.0 ~127.255.255.255:00000000 00000000 00000000 00000000 ~ 0111…...

HTML5基本语法
文章目录 HTML5基本语法一、基础标签1、分级标题2、段标签3、换行及水平线标签4、文本格式标签 二、图片标签1、格式2、属性介绍 三、音频标签1、格式2、属性介绍 四、视频标签1、格式2、属性介绍 五、链接标签1、格式2、显示特点3、属性介绍4、补充(空链接…...

正则表达式常用表示
视频教程:10分钟快速掌握正则表达式 正则表达式在线测试工具(亲测好用):测试工具 正则表达式常用表示 限定符 a*:a出现0次或多次a:a出现1次或多次a?:a出现0次或1次a{6}:a出现6次a…...

【OpenHarmony4.1 之 U-Boot 2024.07源码深度解析】007 - evb-rk3568_defconfig 配置编译全过程
【OpenHarmony4.1 之 U-Boot 2024.07源码深度解析】007 - evb-rk3568_defconfig 配置编译全过程 一、编译后目录列表二、make distclean三、生成.config文件:make V=1 ARCH=arm64 CROSS_COMPILE=aarch64-linux-gnu- evb-rk3568_defconfig四、开始编译:CROSS_COMPILE=aarch64-…...

11.1 Go 标准库的组成
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「stormsha的主页」…...
【UG\NX二次开发】UF 调用Grip例子(实现Grip调用目标dll)(UF_call_grip)
此例子是对:【UG\NX二次开发】UF 加载调用与卸载目标dll(UF_load_library、UF_unload_library)_ug二次开发dll自动加载-CSDN博客的补充。 ①创建txt文本,编写以下内容(功能:接收路径,调用该路径的dll)。改后缀为Grip文件(.grs)。…...

[算法刷题积累] 两数之和以及进阶引用
两数之和很经典,通常对于首先想到的就是暴力的求解,当然这没有问题,但是我们如果想要追求更优秀算法,就需要去实现更加简便的复杂度。 这里就要提到我们的哈希表法: 我们可以使用unordered_map去实现,也可以根据题目&a…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
