【LeetCode刷题】面试题 17.19. 消失的两个数字
- 1. 题目链接
- 2. 题目描述
- 3. 解题方法
- 4. 代码
1. 题目链接
面试题 17.19. 消失的两个数字
2. 题目描述

3. 解题方法
例子假设:
数组A元素为 :1 ,4,5
缺少的元素为:2, 3
那么所有整数就为1 ~ 5,我称这些整数为数组B
此时就有如下的图示:

第1步,此时将A、B两个数组的元素都异或起来,所得到的结果就是2 ^ 3,为了后面的讲解
我将2成为a,3称为b。
第2步,找到a和b(异或)比特位上为1的那一位
2 : 0 1 0
3 : 0 1 1
找到的这一位,我在这里叫做第x位
第3步,根据第x位的不同,划分两类进行异或求得结果
根据上面的例子
1 : 0 0 1
5 : 1 0 1
过程 : 3 ^ 1 ^ 1 ^ 5 ^ 5 (相同的两个数字异或直接为0,0异或任何数字为数字本身)
这一类划分到 3 这里进行异或,就得到了唯一的3
4 : 0 1 0
过程 : 2 ^ 4 ^ 4 (相同的两个数字异或直接为0,0异或任何数字为数字本身)
这一类划分到 2 这里进行异或,就得到了唯一的2
4. 代码
class Solution {
public:vector<int> missingTwo(vector<int>& nums) {// 1. 把所有相同的数都异或起来, 获得a ^ bint tmp = 0;for(auto e : nums) tmp ^= e;for(int i = 1; i <= nums.size() + 2; i++) tmp ^= i;// 2. 找到a ^ b 比特位为 1 的那一位int diff = 0;while(1){if((tmp >> diff) & 1 == 1) break;else diff ++;}// 3. 划分两类数字int a = 0, b = 0;for(auto e : nums){if((e >> diff) & 1 == 1) a ^= e;else b ^= e;}for(int i = 1; i <= nums.size() + 2; i++){if((i >> diff) & 1 == 1) a ^= i;else b ^= i;}return {a, b};}
};
最后附上我的打卡记录,希望各位大佬可以监督我。
相关文章:

【LeetCode刷题】面试题 17.19. 消失的两个数字
1. 题目链接2. 题目描述3. 解题方法4. 代码 1. 题目链接 面试题 17.19. 消失的两个数字 2. 题目描述 3. 解题方法 例子假设: 数组A元素为 :1 ,4,5 缺少的元素为:2, 3 那么所有整数就为1 ~ 5ÿ…...
如何定制Spring的错误json信息
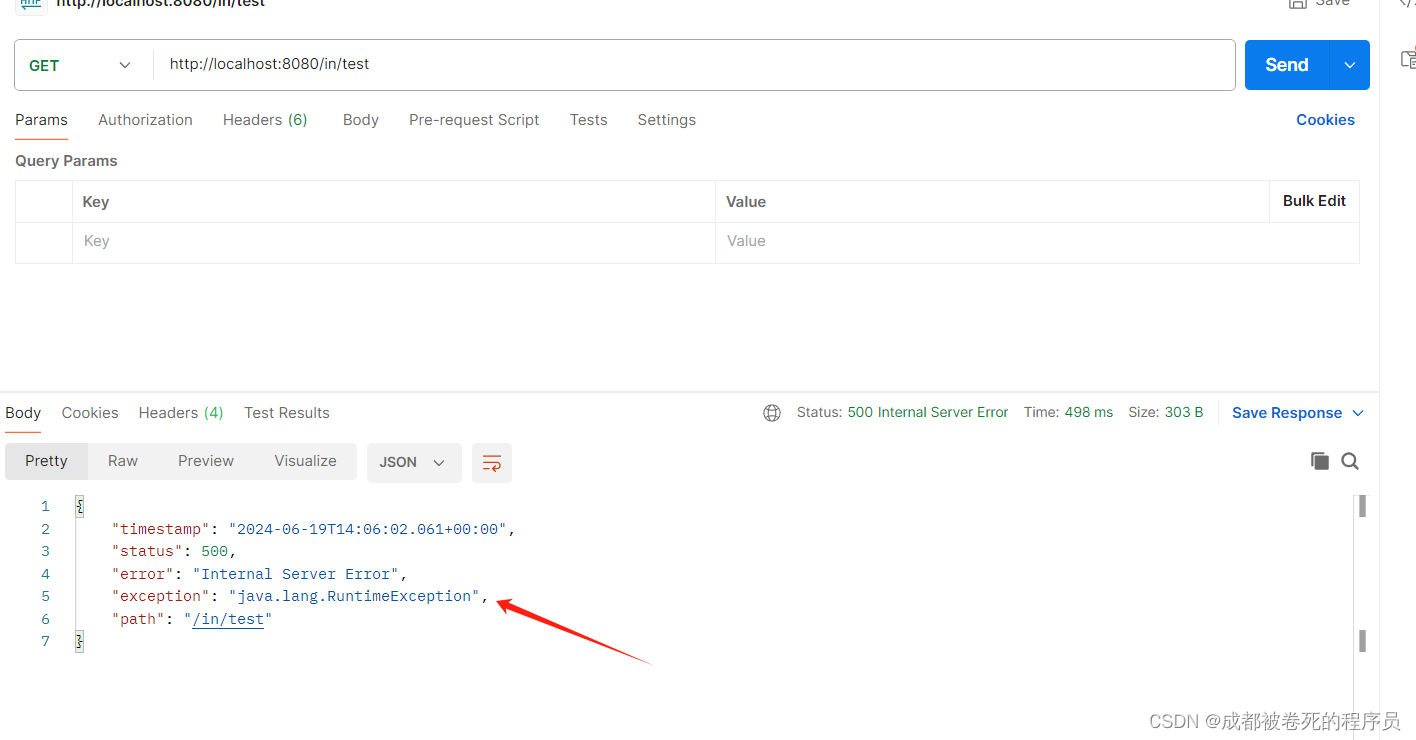
一,前言 相信很多同学都有遇到过这样的spring错误信息。 在我们没有做catch处理时或者做全局的exceptionHandle时,Spring遇到抛出向外的异常时,就会给我们封装返回这么个格式的异常信息。 那么问题来了,我们能否对这个返回增加错…...

【第20章】Vue实战篇之Vue Router(路由)
文章目录 前言一、使用Vue-Router1.安装2. 创建路由器实例3. 注册路由器插件4. 根组件 二、访问路由器1.理论2.使用3. 展示 三、嵌套路由(子路由)1. 准备文件2. 配置路由3. 菜单配置4. 展示 总结 前言 Vue Router 是 Vue.js 的官方路由。它与 Vue.js 核心深度集成,…...
阿里云运维第一步(监控):开箱即用的监控
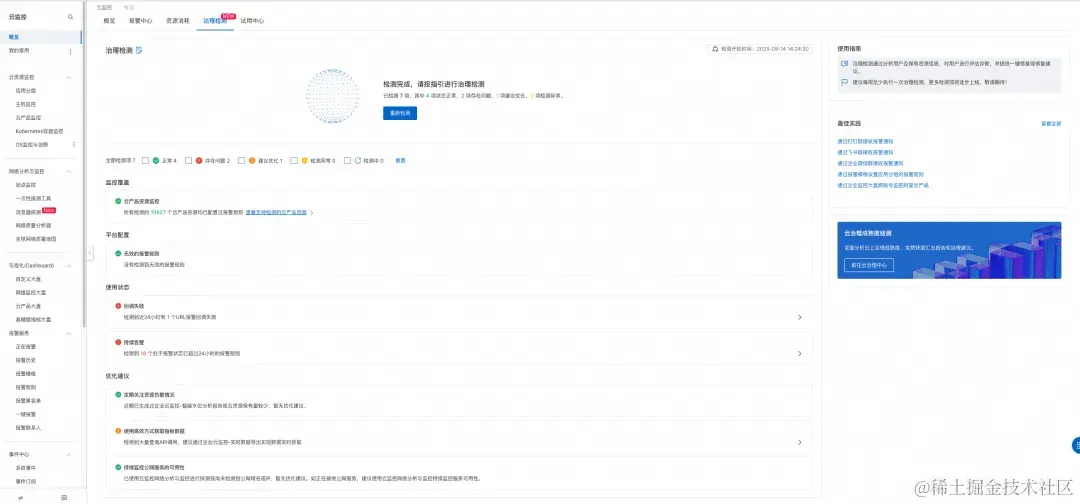
作者:仲阳 这是云的时代,现在云计算已经在各行各业广泛的应用。但是上云对于大多数客户来说,依然有很大的学习成本,如下图仅是阿里云都有几百款产品,怎么选择?怎么用?对于客户来说都是问题。“…...

Python量化交易学习——Part7:定制增强型中证红利策略
中证红利指数是一个反映A股市场高红利股票整体状况和走势的指数。它通过选取上海、深圳交易所中现金股息率高、分红比较稳定、具有一定规模及流动性的100只股票作为样本。这个指数的目的是提供一个全面且具有代表性的视角,以观察A股市场中高红利股票的表现。中证红利指数的样本…...

拥抱未来:探索改变游戏规则的新存储技术
目录 一.存储级内存(Storage-Class Memory) 3D XPoint 技术 特点 应用场景 优点 缺点 适用场景 示例 二.QLC NAND闪存 概述 优点 缺点 适用场景 前景展望 三.DNA存储 概述 优点 原理 实际应用 关键问题 研究进展 适用场景 分布式…...
shell中的流程控制
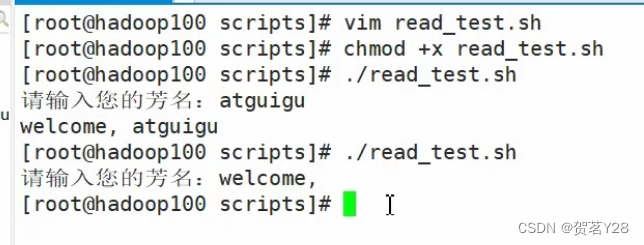
条件判断在流程控制中的重要性 有了条件判断才能进行if判断即分支流程,才能进行case的多分支流程,才能进行for循环和while循环。 单分支流程判断 如上图所示,在shell编程中常使用英文状态下的分号来在Linux控制台一次性执行多条命令&#x…...
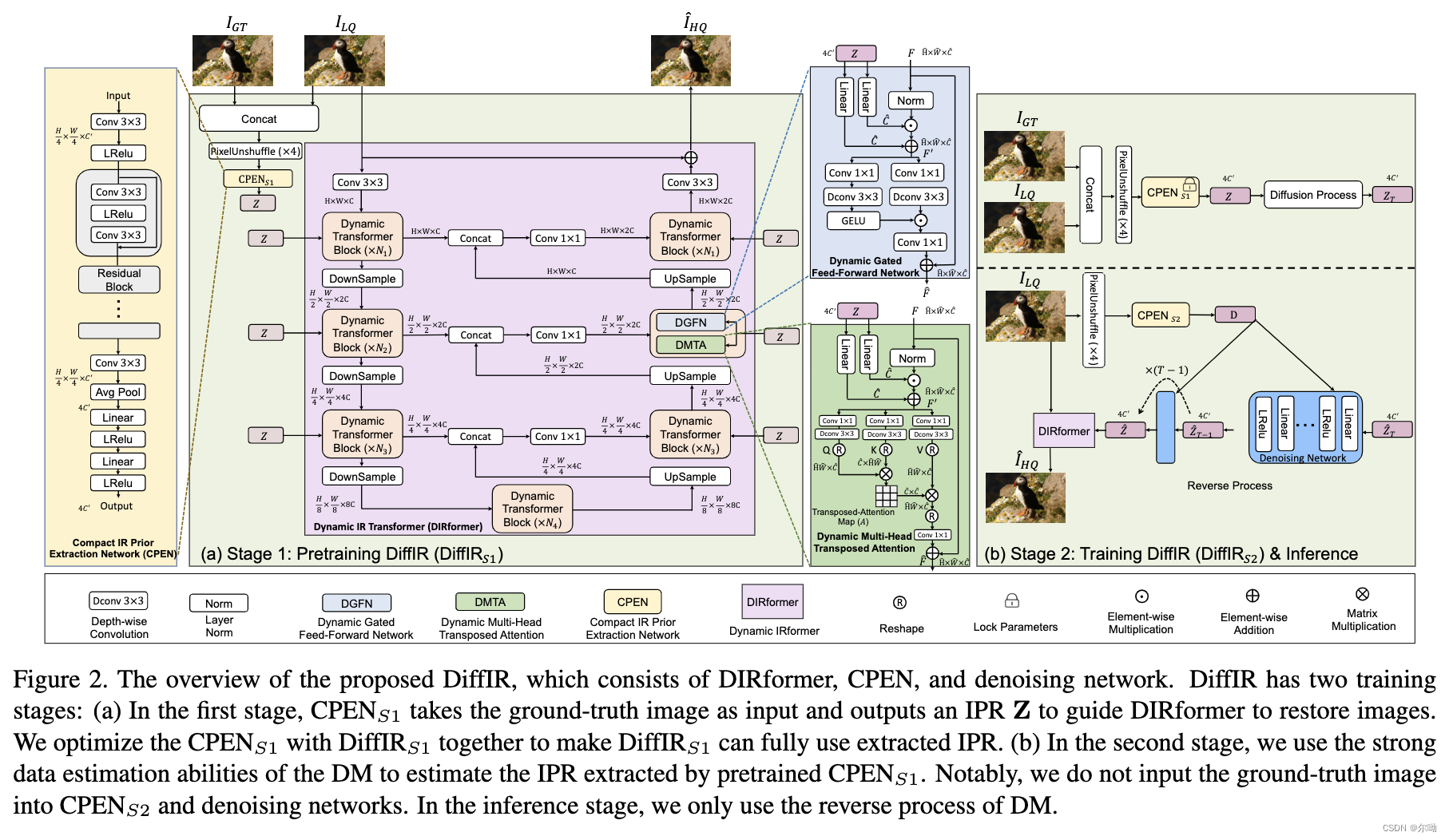
DiffIR: Efficient Diffusion Model for Image Restoration
清华Ð&字节&UTDhttps://github.com/Zj-BinXia/DiffIR 问题引入 IR任务和image synthesis任务不同点是IR任务本身有一个很强的低质量图片作为先验,所以可以不完全遵循图片生成的范式,本文主要在compact的IPR空间进行DM;本文提…...
xss一些笔记
(乱写的一些笔记) innerHTML只防script像是img就不会防 innerText都防 上面代码执行避免用户交互 js也可以用’‘执行 例子 alert’1‘ document.location.hash // #号后的部分,包括#号 document.location.host // 域名…...

以太坊网络中为什么要设置Gas上限
以太坊网络中的Gas上限(Gas Limit)是一个重要的机制,它主要出于以下几个目的: 防止无限循环和拒绝服务攻击(DoS): Gas上限防止了智能合约中的无限循环,这可以保护网络免受恶意合约的…...
vue-cli是什么?和 webpack是什么关系?
前言 Vue CLI是Vue.js项目的官方脚手架,基于Node.js与Webpack构建。安装Vue CLI前需确保Node.js已安装,随后通过npm全局安装。Vue CLI能迅速创建和管理Vue.js项目,提升开发效率。而Webpack则负责资源打包,通过配置文件管理依赖、插…...
leetcode刷题(46-50)
算法是码农的基本功,也是各个大厂必考察的重点,让我们一起坚持写题吧。 遇事不决,可问春风,春风不语,即是本心。 我们在我们能力范围内,做好我们该做的事,然后相信一切都事最好的安排就可以啦…...
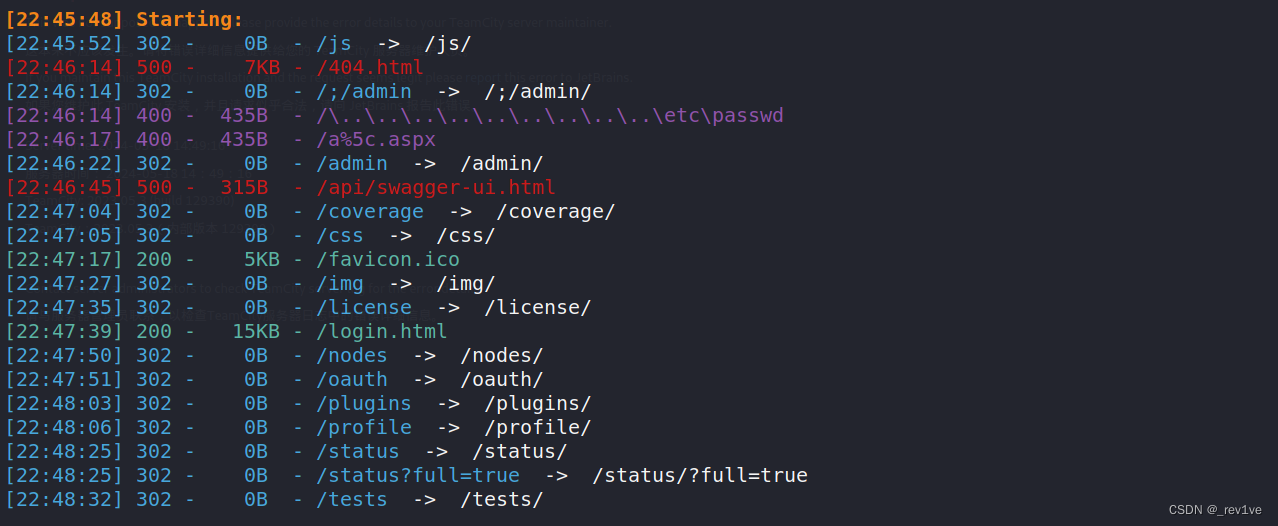
[渗透测试学习] Runner-HackTheBox
Runner-HackTheBox 信息搜集 nmap扫描端口 nmap -sV -v 10.10.11.13扫描结果如下 PORT STATE SERVICE VERSION 22/tcp open ssh OpenSSH 8.9p1 Ubuntu 3ubuntu0.6 (Ubuntu Linux; protocol 2.0) 80/tcp open http nginx 1.18.0 (Ubuntu) 8000…...

keil5显示内存和存储占用百分比进度条工具
简介 [Keil5_disp_size_bar] 以进度条百分比来显示keil编译后生成的固件对芯片的内存ram和存储flash的占用情况, 并生成各个源码文件对ram和flash的占比整合排序后的map信息的表格和饼图。 原理是使用C语言遍历当前目录找到keil工程和编译后生成的map文件 然后读取工程文件和m…...

示例:推荐一个应用Adorner做的消息对话框
一、目的:开发过程中,经常用到对话框,下面演示一个应用Adorner做的带遮盖层蒙版的控件,使用MainWindow的Adorner实现不需要额外定义遮盖层,使用Object作为参数,可自定义DataTemplate定制消息显示样式 二、效…...
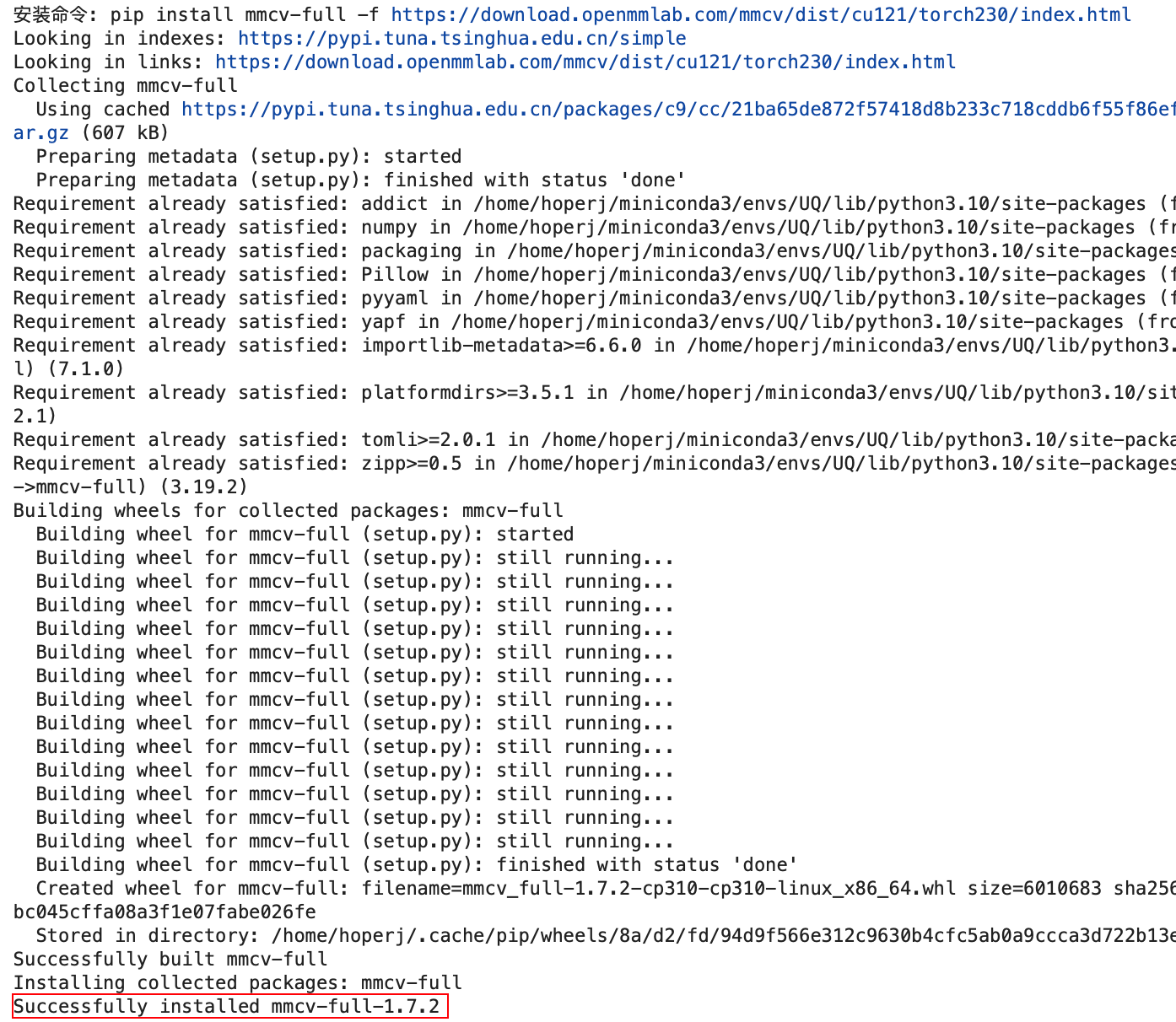
Building wheels for collected packages: mmcv, mmcv-full 卡住
安装 anime-face-detector 的时候遇到一个问题:Installation takes forever #1386:在构建mmcv-full时卡住,这里分享下解决方法(安装 mmcv 同理,将下面命令中的 mmcv-full 替换成 mmcv) 具体表现如下&#x…...

可视化表单拖拽生成器优势多 助力流程化办公!
当前,很多企业需要实现流程化办公,进入数字化转型时期。要想实现这一目标,就需要借助更优质的平台产品。低代码技术平台是得到企业喜爱的发展平台,拥有可视化操作、灵活、高效、更可靠等优势特点,在推动企业实现流程化…...
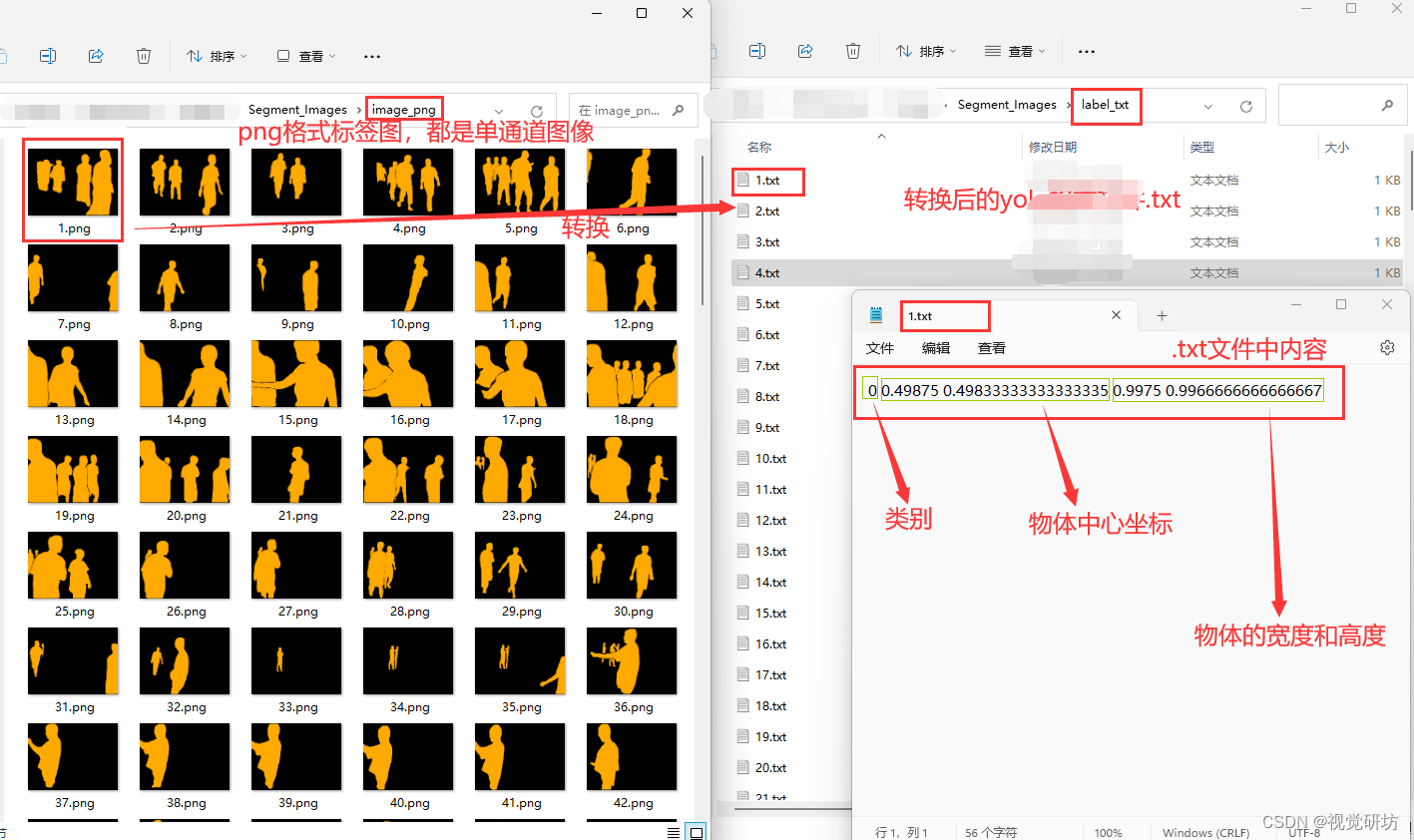
数据集制作——语义分割前png、jpg格式标签图转yolo格式.txt文件(附代码)
💪 专业从事且热爱图像处理,图像处理专栏更新如下👇: 📝《图像去噪》 📝《超分辨率重建》 📝《语义分割》 📝《风格迁移》 📝《目标检测》 📝《暗光增强》 &a…...
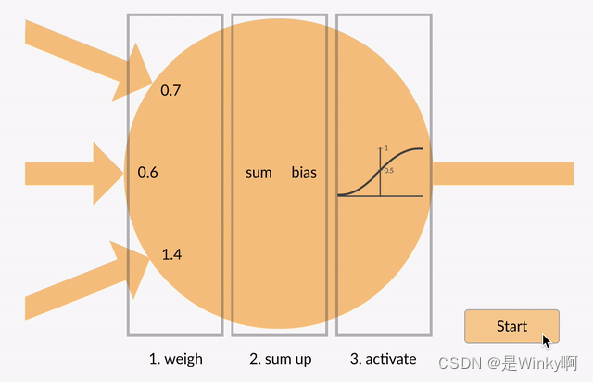
机器学习课程复习——ANN
Q:ANN? 基本架构 由输入层、隐藏层、输出层等构建前馈/反馈传播 工作原理 先加权求和:每个神经元的输出是输入加权和的激活再送入激活函数:激活函数的存在使得其能够拟合各类非线性任务 联想:像adaboosting的加权求…...

C++回溯算法(2)
棋盘问题 #include<bits/stdc.h> using namespace std; void func(int,int); bool tf(int,int); void c(); int n,k; char a[110][110]; int cnt20; int main() {cin>>n>>k;for(int i0;i<n;i){for(int j0;j<n;j){cin>>a[i][j];}}func(0,0);cout…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...
