当前位置： 首页 > news >正文

华为OD机试真题2024版-求幸存数之和

news 文章来源：https://blog.csdn.net/weixin_43106895/article/details/139844286 2024/10/23 2:41:10

题目描述\n给一个正整数列 nums，一个跳数 jump，及幸存数量 left。运算过程为：从索引为 0 的位置开始向后跳，中间跳过 J 个数字，命中索引为 J+1 的数字，该数被敲出，并从该点起跳，以此类推，直到幸存 left 个数为止。然后返回幸存数之和。\n约束：

1、0 是第一个起跳点。

2、起跳点和命中点之间间隔 jump 个数字，已被敲出的数字不计入在内。

3、跳到末尾时无缝从头开始（循环查找），并可以多次循环。

4、若起始时 left>len(nums) 则无需跳数处理过程。

/**
* nums: 正整数数列，长度范围 [1,10000]
* jump: 跳数，范围 [1,10000]
* left: 幸存数量，范围 [0,10000]
* return: 幸存数之和
*/
int sumOfLeft(int[] nums,int jump,int left)

输入

[1,2,3,4,5,6,7,8,9],4,3

输出

13

说明\n从 1（索引为 0）开始起跳,中间跳过 4 个数字,因此依次删除 6,2,8,5,4,7 。 剩余 1,3,9,返回和为 13\n\nOD 统一题解

import java.util.ArrayList;
import java.util.List;public class Main {public static int solve(List<Integer> nums, int jump, int left)

相关文章：

华为OD机试真题2024版-求幸存数之和

题目描述\n给一个正整数列 nums，一个跳数 jump，及幸存数量 left。运算过程为：从索引为 0 的位置开始向后跳，中间跳过 J 个数字，命中索引为 J+1 的数字，该数被敲出，并从该点起跳，以此类推，直到幸存 left 个数为止。然后返回幸存数之和。\n约束： 1、0 是第一个起跳点。…...

编程日记 2024/6/21 2:27:35

Python - 各种计算器合集【附源码】

计算器合集 一&#xff1a;极简版计算器二&#xff1a;简易版计算器三&#xff1a;不简易的计算器四&#xff1a;还可以计算器 一&#xff1a;极简版计算器 运行效果&#xff1a; import tkinter as tk import tkinter.messagebox win tk.Tk() win.title("计算器")…...

编程日记 2024/6/21 2:26:33

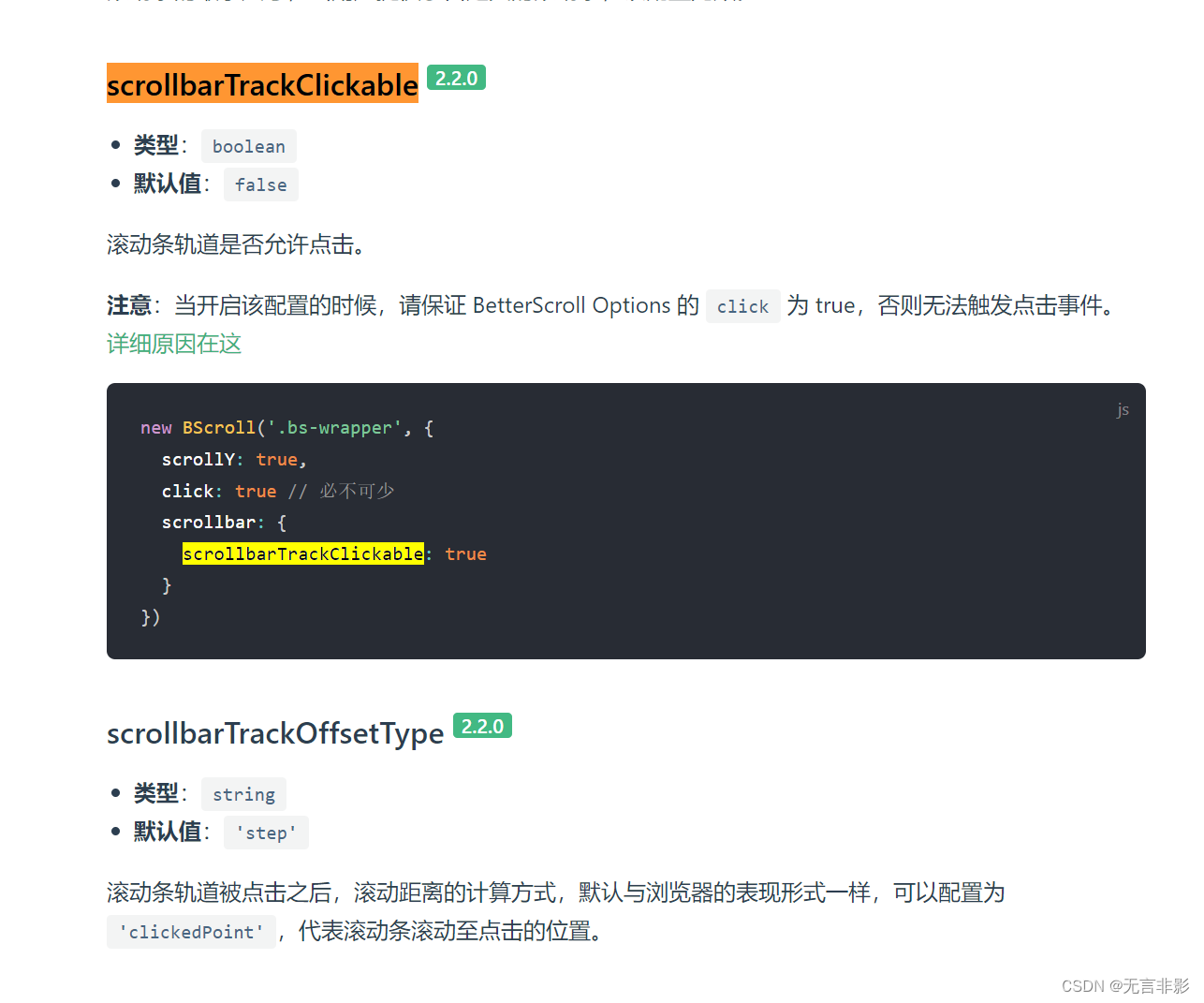
【已解决】better-scroll在PC端如何开启鼠标滚动以及如何始终显示滚动条

总结 需要安装插件 mouse-wheel 和 scrollbar 在PC端如何开启鼠标滚动? 需要安装官方提供的滚动插件&#xff1a;mouse-wheel https://better-scroll.github.io/docs/zh-CN/plugins/mouse-wheel.html 为了开启鼠标滚动功能&#xff0c;你需要首先引入 mouseWheel 插件&…...

编程日记 2024/6/21 2:24:30

AJAX 综合案例-day2

Bootstrap 弹框 功能&#xff1a;不离开当前页面&#xff0c;显示单独内容&#xff0c;供用户操作 步骤&#xff1a; 1. 引入 bootstrap.css 和 bootstrap.js 2. 准备 弹框标签 &#xff0c;确认结构 3. 通过 自定义属性 &#xff0c;控制弹框的 显示 和 隐藏 1. 通过属性…...

编程日记 2024/6/21 2:23:27

【Esp32连接微信小程序蓝牙】附Arduino源码《 返回10007 相同特征id冲突问题》

前言 最近接了一个外包&#xff0c;发现了esp32连接小程序会有很多bug&#xff0c;所以接下来会慢慢更新解决方案&#xff0c;还是需要多接触项目才能进步呀兄弟们&#xff01; 附上uuid的生成链接&#xff1a; // See the following for generating UUIDs: // https://www.uu…...

编程日记 2024/6/21 2:22:26

并发控制技术

事物的隔离性实现主要依赖于多种并发控制技术，这些技术确保在并发执行的事物中，一个事物的操作不会被其他事物干扰。并发控制技术按照其对可能冲突的操作采取的不同策略可以分为乐观并发控制和悲观并发控制两大类。 基于封锁的并发控制 对于并发可能冲突的操作，比如读-写，…...

编程日记 2024/6/21 2:21:24

什么是网段

一、A类地址的网段&#xff1a; 情况1&#xff1a;最小的网段就是xxx.0.0.0&#xff0c;直接使用第一段的网络地址做网段。 情况2&#xff1a;如果希望网段允许的主机数量的范围缩小&#xff0c;扩大网段值即可&#xff0c;xxx.xxz.zzz.zzz&#xff0c;比如xxx.xxx.xzz.zzz&…...

编程日记 2024/6/21 2:20:21

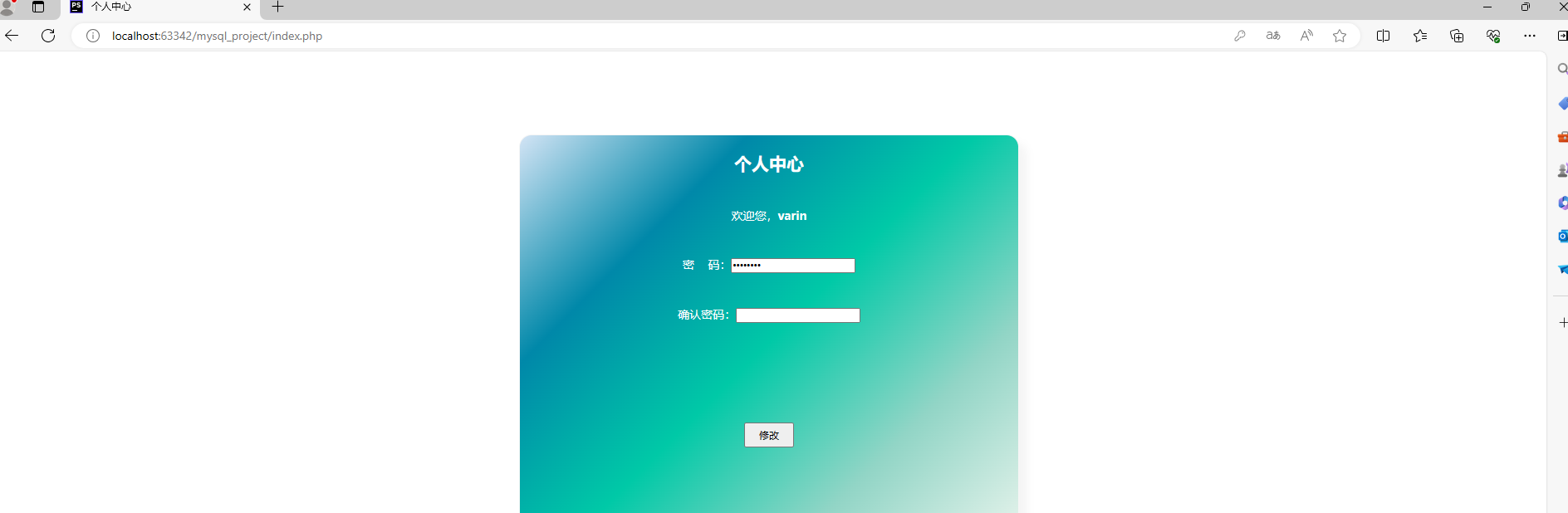
PHP和Mysql前后端交互效果实现

一、连接数据库基本函数 mysqli_connect(); 作用&#xff1a;创建数据库连接&#xff0c;打开一个新的mysql的连接。传参顺序&#xff1a;数据库地址、数据库账号、数据库密码 <?phpecho mysqli_connect("localhost",root,root) ?> /*结果&#xff1a;F…...

编程日记 2024/6/21 2:19:20

vue小总结

知识总结 【 1 】es6 语法总结 # let 定义变量 # const定义常量 ------块级作用域---- # var 以后尽量少用&#xff0c;函数作用域var 在 JavaScript 中是函数作用域或全局作用域。而 let 和 const 是块级作用域。 // 使用 var 声明全局变量 var globalVar "Im a globa…...

编程日记 2024/6/21 2:17:18

RapidLayout:中英文版面分析推理库

引言 继上一篇文章之后&#xff0c;我这里想着将360发布的版面分析模型整合到现有的rapid_layout仓库中&#xff0c;便于大家快速使用。 不曾想到&#xff0c;我这整理工作越做越多了&#xff0c;好在整体都是往更好方向走。 起初&#xff0c;rapid_layout项目是在RapidStru…...

编程日记 2024/6/21 2:16:16

postman 工具下载安装使用教程_postman安装

本文讲解的是postman工具下载、Postman安装步骤、postman下载、postman安装教程。Postman是一款流行的API测试工具&#xff0c;它提供了一个用户友好的界面&#xff0c;用于发送和测试API请求&#xff0c;并且可以轻松地按需管理和组织请求。 这使得开发人员和测试人员能够更高…...

编程日记 2024/6/21 2:14:13

【数学建模】——【新手小白到国奖选手】——【学习路线】

专栏&#xff1a;数学建模学习笔记 目录 ​编辑 第一阶段&#xff1a;基础知识和工具 1.Python基础 1.学习内容 1.基本语法 2.函数和模块 3.面向对象编程 4.文件操作 2.推荐资源 书籍&#xff1a; 在线课程&#xff1a; 在线教程&#xff1a; 2.数学基础 1.学习内…...

编程日记 2024/6/21 2:13:12

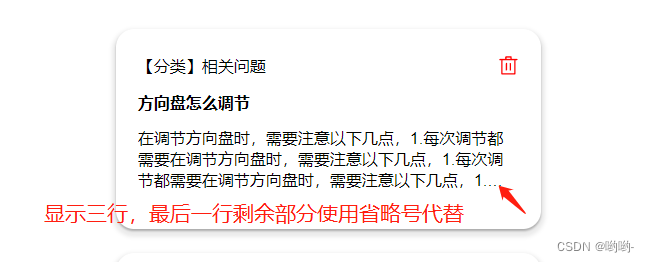
CSS文本超限后使用省略号代替

方案一&#xff1a; 只显示一行&#xff0c;超限后使用省略号代替 .detail {overflow: hidden;text-overflow: ellipsis;white-space: nowrap; }方案二&#xff1a; 显示多行&#xff0c;到最后一行还没有显示完&#xff0c;则最后一行多出来的部分使用省略号代替。 .detai…...

编程日记 2024/6/21 2:12:10

多线程下JVM内存模型 和 volatile关键字

1、线程的概念 线程&#xff08;thread&#xff09;是操作系统能够进行运算调度的最小单位。它被包含在进程之中&#xff0c;是进程中的实际运作单位。一条线程指的是进程中一个单一顺序的控制流&#xff0c;一个进程中可以并发多个线程&#xff0c;每条线程并行执行不同的任务…...

编程日记 2024/6/21 2:11:09

Uniapp实现页面滚动Tab吸顶，点击tab内容滚动到对应tab内容位置

思路&#xff1a;运用uniapp原生提供方法uni.createSelectorQuery()获取滚动对应节点的信息&#xff0c;即节点距离页面顶部的距离&#xff0c;再通过uniapp原生监听页面滚动事件onPageScroll&#xff0c;获取页面内容滚动的高度&#xff0c;二者相加即定位到对应节点的滚动距离…...

编程日记 2024/6/21 2:10:08

在Elasticsearch中-SpaceJam一个全文搜索的实例

在Elasticsearch中进行全文搜索通常涉及几个步骤&#xff1a;创建索引、定义映射、索引文档、执行搜索查询。下面我将通过一个名为"SpaceJam"的虚构实例来演示如何进行全文搜索。 ### 步骤 1: 创建索引 首先&#xff0c;我们需要创建一个索引。在这个例子中&#x…...

编程日记 2024/6/21 2:09:07

Microsoft Edge浏览器安装crx拓展插件教程

1、首先打开edge浏览器&#xff0c;点击顶部地址栏。 2、在地址栏中输入"edge://flags/#extensions-on-edge-urls"并按下回车。2、在地址栏中输入"edge://flags/#extensions-on-edge-urls"并按下回车。 3、进入后&#xff0c;将图示选项改为“已禁用”。 …...

编程日记 2024/6/21 2:07:03

陈晓婚前婚后大变样

陈晓婚前婚后大变样&#xff1f;陈妍希揭秘甜蜜与现实的碰撞在娱乐圈的星光璀璨中&#xff0c;有一对夫妻总是津津乐道&#xff0c;那就是陈晓和陈妍希。他们的爱情故事&#xff0c;从荧幕到现实&#xff0c;一直备受关注。然而&#xff0c;近日陈妍希在节目中透露&#xff0c;…...

编程日记 2024/6/21 2:06:02

Linux sudo -i取消密码的方法

直接修改 /etc/sudoers 文件来实现 sudo -i 无需密码的配置。以下是具体步骤&#xff1a; 步骤 打开终端并使用 visudo 命令编辑 /etc/sudoers 文件 使用 visudo 编辑 sudoers 文件是推荐的方法&#xff0c;因为它会在保存前进行语法检查&#xff0c;防止出现配置错误。 sudo …...

编程日记 2024/6/21 2:05:01

PMP考试多少分才算合格通过？

PMP是美国颁发的专业资格认证,其考试采用的是国外的评分体系。考试内容被划分为3大部分:人、过程和商业环境,每个部分所占的权重不同。考试形式为180个单选和多选题,其中有25题不计分。考试可能会抽到错误或未回答的题目,也可能抽到正确答题的题目。最终根据NBTA的4个等级进行综…...

编程日记 2024/6/21 2:04:00

原生js写数据自动纵向滚动，鼠标移入后停止滚动可手动滚动，鼠标移出转自动

<!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>滚动页面</title><link rel"styleshee…...

编程日记 2024/6/21 2:02:58

板凳----Linux/Unix 系统编程手册 25章 进程的终止

25.1 进程的终止&#xff1a;_exit()和exit() 440 1. _exit(int status)&#xff0c; status 定义了终止状态&#xff0c;父进程可调用 wait 获取。仅低8位可用&#xff0c;调用 _exit() 总是成功的。 2.程序一般不会调用 _exit()&#xff0c; 而是调用库函数 exit()。exit() …...

编程日记 2024/6/21 2:00:54

若依Ruoyi-vue和element admin的区别，该如何选择。

提到中后台的前端框架&#xff0c;每个人都能列举出很多&#xff0c;这其中提及率比较高的就是Ruoyi和element admin两款&#xff0c;很多小伙伴分不清二者&#xff0c;本文为大家详细讲解一下。 一、若依Ruoyi-vue是什么&#xff1f; 若依Ruoyi-Vue是一款基于 Vue.js 开发的…...

编程日记 2024/6/21 1:59:52

Sklearn之朴素贝叶斯应用

目录 sklearn中的贝叶斯分类器 前言 1 分类器介绍 2 高斯朴素贝叶斯GaussianNB 2.1 认识高斯朴素贝叶斯 2.2 高斯朴素贝叶斯建模案例 2.3 高斯朴素贝叶斯擅长的数据集 2.3.1 三种数据集介绍 2.3.2 构建三种数据 2.3.3 数据标准化 2.3.4 朴素贝叶斯处理数据 2.4 高斯…...

编程日记 2024/6/21 1:58:51

网络编程（二）TCP编程 TCP粘包问题

文章目录 一、TCP网络编程&#xff08;一&#xff09;流程&#xff08;二&#xff09;相关函数1. socket2. bind3. listen4. accept5. connect 二、收发函数&#xff08;一&#xff09;send函数&#xff08;二&#xff09;recv函数 三、TCP粘包问题&#xff08;一&#xff09;将…...

编程日记 2024/6/21 1:57:50

【总线】AXI总线：FPGA设计中的通信骨干

目录 AXI4&#xff1a;高性能地址映射通信的基石 AXI4-Lite&#xff1a;轻量级但功能强大的通信接口 AXI4-Stream&#xff1a;高速流数据传输的利器 结语&#xff1a;AXI总线在FPGA设计中的重要性 大家好,欢迎来到今天的总线学习时间!如果你对电子设计、特别是FPGA和SoC设计…...

编程日记 2024/6/21 1:56:48

Cesium源码解析六（3dtiles属性获取、建筑物距离计算、建筑物着色及其原理分析）

快速导航 Cesium源码解析一&#xff08;搭建开发环境&#xff09; Cesium源码解析二&#xff08;terrain文件的加载、解析与渲染全过程梳理&#xff09; Cesium源码解析三&#xff08;metadataAvailability的含义&#xff09; Cesium源码解析四&#xff08;metadata元数据拓展…...

编程日记 2024/6/21 1:54:45

AI 情感聊天机器人之旅 —— 相关论文调研

开放域闲聊场景 Prompted LLMs as Chatbot Modules for Long Open-domain Conversation 发布日期&#xff1a;2023-05-01 简要介绍&#xff1a;作者提出了 MPC&#xff08;模块化提示聊天机器人&#xff09;&#xff0c;这是一种无需微调即可创建高质量对话代理的新方法&…...

编程日记 2024/6/21 1:53:42

WPF Prism框架搭建

WPF Prism框架搭建 1.引入Prism框架 在Nuget包管理器中搜索Prism&#xff0c;并添加到项目中 2.在项目中使用prism框架 2.1 修改app.xaml 删除项目中自带的StartupUri 修改Application节点为prism:PrismApplication 引入prism命名空间 <prism:PrismApplication x:C…...

编程日记 2024/6/21 1:52:40

MyBatisplus使用报错--Invalid bound statement

报错如下 org.apache.ibatis.binding.BindingException: Invalid bound statement (not found): com.lotus.mybatis.mapper.UserMapper.selectListat org.apache.ibatis.binding.MapperMethod$SqlCommand.<init>(MapperMethod.java:235)at com.baomidou.mybatisplus.cor…...

编程日记 2024/6/21 1:50:38

如何在服务器建设iis网站/宁德市人民医院

1.Linux就是电脑操作系统 就是对系统里面文件、创建、写入、删除、和git上传文件等对电脑系统的操作 2.一般是WinR&#xff08;输入CMD&#xff09;在里面操作...

编程日记 2024/10/23 0:42:09

做网站找哪家好熊掌号/2022最火营销方案

DSpace 1.5版本对统计功能做了比较多的更新。 配置好config目录下的dstat.dat文件 # the year and month to start creating reports from # - year as four digits (e.g. 2005) 开始统计的年份 # - month as a number (e.g. January is 1, December is 12)开始统计的月份 st…...

编程日记 2024/10/23 0:40:09

网站里的横幅怎么做/百度竞价外包

Img格式文件可以使用ArcGis或者envi软件打开&#xff0c;这里介绍envi软件的安装过程。 1. 安装环境 操作系统&#xff1a;win10 软件版本&#xff1a;5.1 软件下载地址&#xff1a; 2. 安装步骤 进入软件安装包路径&#xff1b;2. 双击IDL83ENVI51win64.exe开始安装&…...

编程日记 2024/10/22 22:48:45

自己做网站卖产品怎么样/seo和sem的区别与联系

sql优化无止境&#xff0c;最近在写sql的时候&#xff0c;用到了mysql中排序&#xff0c;然后需要某个行业在排序排名&#xff0c;优化了很久&#xff0c;还是不能达到理想的效果&#xff0c;国内博客网站也搜了很多&#xff0c;最后从歪果仁那里发现了解决的方法&#xff0c;歪…...

编程日记 2024/10/22 22:32:56

wordpress密码对的登不不了/电商代运营十大公司排名

直接使用df.drop_duplicates()就可以获取去重复完毕的DataFrame了 df.drop_duplicates(inplaceTrue) 参考别人的经验&#xff1a;https://blog.csdn.net/qq_24499417/article/details/81126807...

编程日记 2024/10/22 19:34:45

飞虎队网站建设/百度服务中心人工客服

实验一 求整数和、切pizza和Hanoi塔等问题的求解 一&#xff0c;实验描述 用C语言编程实现求整数和&#xff0c;切pizza以及Hanoi塔等问题的求解&#xff0c;在程序中加入clock ()来计算求解时间&#xff0c;使用不同的输入值得到对应的时间值。分析算法的时间复杂度并与测量…...

编程日记 2024/10/22 17:59:02