DP:完全背包+多重背包问题

完全背包和01背包的区别就是:可以多次选
一、完全背包(模版)
【模板】完全背包_牛客题霸_牛客网
#include <iostream>
#include<string.h>
using namespace std;
const int N=1001;
int n,V,w[N],v[N],dp[N][N];
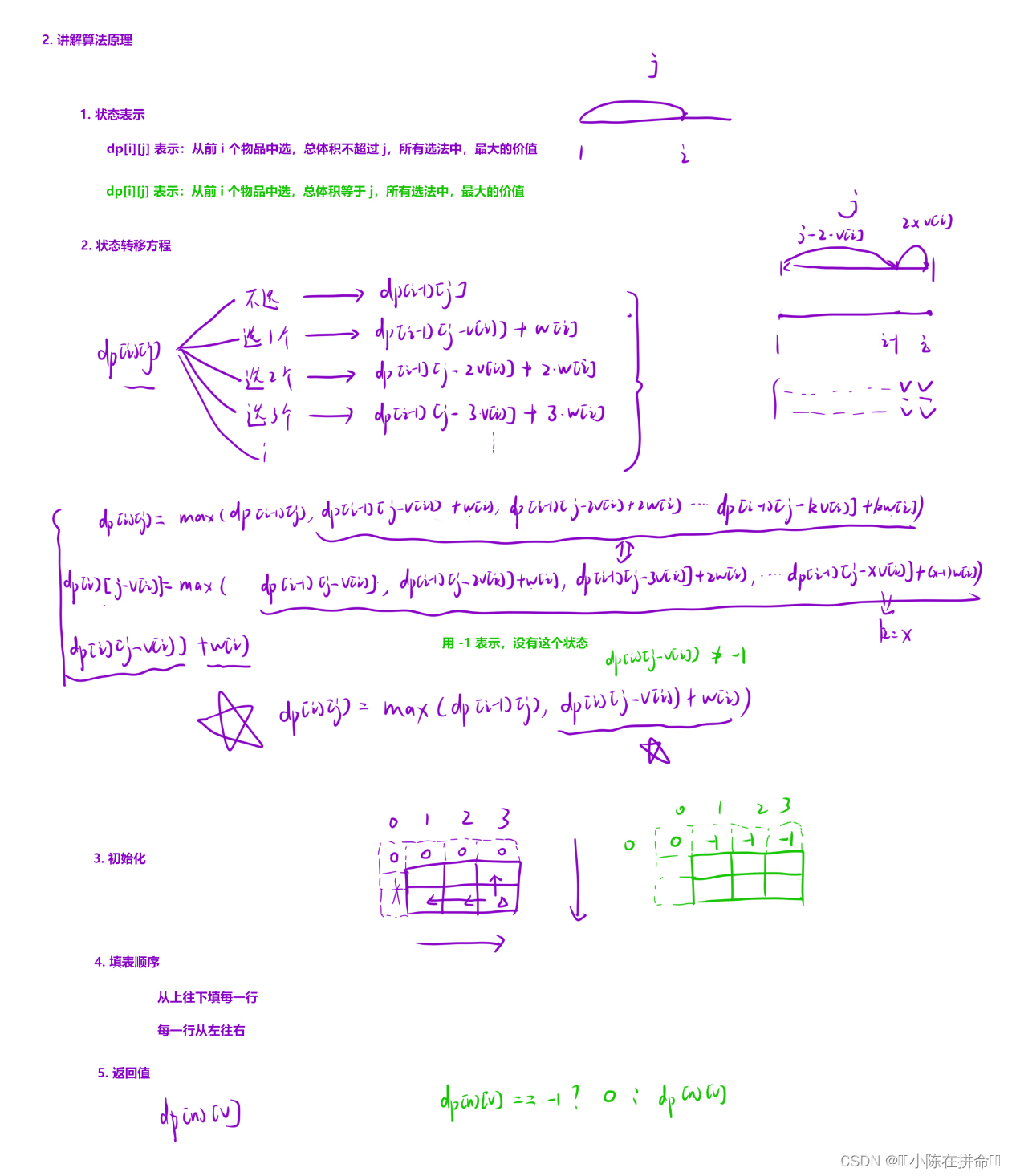
//dp[i][j]表示从前i个物品选,体积不超过j的最大价值
//dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i],dp[i-1][j-2v[i]]+2w[i]……)
//数学dp[i][j-v[i]]=max(dp[i-1][j-v[i]],dp[i-1][j-2v[i]]+w[i]……)
//dp[i][j]=max(dp[i-1][j],dp[i][j-v[i]])
int main()
{cin>>n>>V;for(int i=1;i<=n;++i) cin>>v[i]>>w[i];//解决第一问for(int i=1;i<=n;++i)for(int j=1;j<=V;++j){dp[i][j]=dp[i-1][j];if(j>=v[i]) dp[i][j]=max(dp[i][j],dp[i][j-v[i]]+w[i]);} cout<<dp[n][V]<<endl;//解决第二问 //dp[i][j]表示从前i个物品选,体积正好为j的最大价值memset(dp,0,sizeof dp);//约定-1表示状态选不到 当i=0时 j>=1时 必然是没有状态的for(int j=1;j<=V;++j) dp[0][j]=-1;for(int i=1;i<=n;++i)for(int j=1;j<=V;++j){dp[i][j]=dp[i-1][j];if(j>=v[i]&&dp[i][j-v[i]]!=-1) dp[i][j]=max(dp[i][j],dp[i][j-v[i]]+w[i]);} cout<<(dp[n][V]==-1?0:dp[n][V])<<endl;return 0;
}滚动数组的优化策略:
 区分:01背包的优化得是从右往左,而完全背包的优化得是从左往右
区分:01背包的优化得是从右往左,而完全背包的优化得是从左往右
#include <iostream>
#include<string.h>
using namespace std;
const int N=1001;
int n,V,w[N],v[N],dp[N];
//dp[i][j]表示从前i个物品选,体积不超过j的最大价值
//dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i],dp[i-1][j-2v[i]]+2w[i]……)
//数学dp[i][j-v[i]]=max(dp[i-1][j-v[i]],dp[i-1][j-2v[i]]+w[i]……)
//dp[i][j]=max(dp[i-1][j],dp[i][j-v[i]])
int main() //优化必须要从左往右
{cin>>n>>V;for(int i=1;i<=n;++i) cin>>v[i]>>w[i];//解决第一问for(int i=1;i<=n;++i)for(int j=v[i];j<=V;++j)dp[j]=max(dp[j],dp[j-v[i]]+w[i]);cout<<dp[V]<<endl;//解决第二问 //dp[i][j]表示从前i个物品选,体积正好为j的最大价值memset(dp,0,sizeof dp);//约定-1表示状态选不到 当i=0时 j>=1时 必然是没有状态的for(int j=1;j<=V;++j) dp[j]=-0x3f3f3f3f;for(int i=1;i<=n;++i)for(int j=v[i];j<=V;++j)dp[j]=max(dp[j],dp[j-v[i]]+w[i]);cout<<(dp[V]<0?0:dp[V])<<endl;return 0;
}二、零钱兑换
. - 力扣(LeetCode)


class Solution {
public:int coinChange(vector<int>& coins, int amount) {//dp[i][j]表示从前i个里面选 正好凑成j所需要的最少硬币个数//如果不选i dp[i-1][j]//选1个i dp[i-1][j-coins[i-1]]+1//dp[i][j]=min(dp[i-1][j],dp[i-1][j-coins[i-1]]+1,dp[i-1][j-2coins[i-1]]+2……)//dp[i][j-coins[i-1]]=min(dp[i-1][j-coins[i-1]],dp[i-1][j-2coins[i-1]]+1……)//dp[i][j]=min(dp[i-1][j],dp[i][j-coins[i-1]]+1)const int INF=0x3f3f3f3f;int n=coins.size();vector<vector<int>> dp(n+1,vector<int>(amount+1));for(int j=1;j<=amount;++j) dp[0][j]=INF;for(int i=1;i<=n;++i)for(int j=1;j<=amount;++j){dp[i][j]=dp[i-1][j];if(j>=coins[i-1]) dp[i][j]=min(dp[i][j],dp[i][j-coins[i-1]]+1);}return dp[n][amount]>=INF?-1:dp[n][amount];}
};滚动数组优化:
class Solution {
public:int coinChange(vector<int>& coins, int amount) {//dp[i][j]表示从前i个里面选 正好凑成j所需要的最少硬币个数//如果不选i dp[i-1][j]//选1个i dp[i-1][j-coins[i-1]]+1//dp[i][j]=min(dp[i-1][j],dp[i-1][j-coins[i-1]]+1,dp[i-1][j-2coins[i-1]]+2……)//dp[i][j-coins[i-1]]=min(dp[i-1][j-coins[i-1]],dp[i-1][j-2coins[i-1]]+1……)//dp[i][j]=min(dp[i-1][j],dp[i][j-coins[i-1]]+1)const int INF=0x3f3f3f3f;int n=coins.size();vector<int> dp(amount+1,INF);dp[0]=0;for(int i=1;i<=n;++i)for(int j=coins[i-1];j<=amount;++j)dp[j]=min(dp[j],dp[j-coins[i-1]]+1);return dp[amount]>=INF?-1:dp[amount];}
};三、零钱兑换II
. - 力扣(LeetCode)

class Solution {
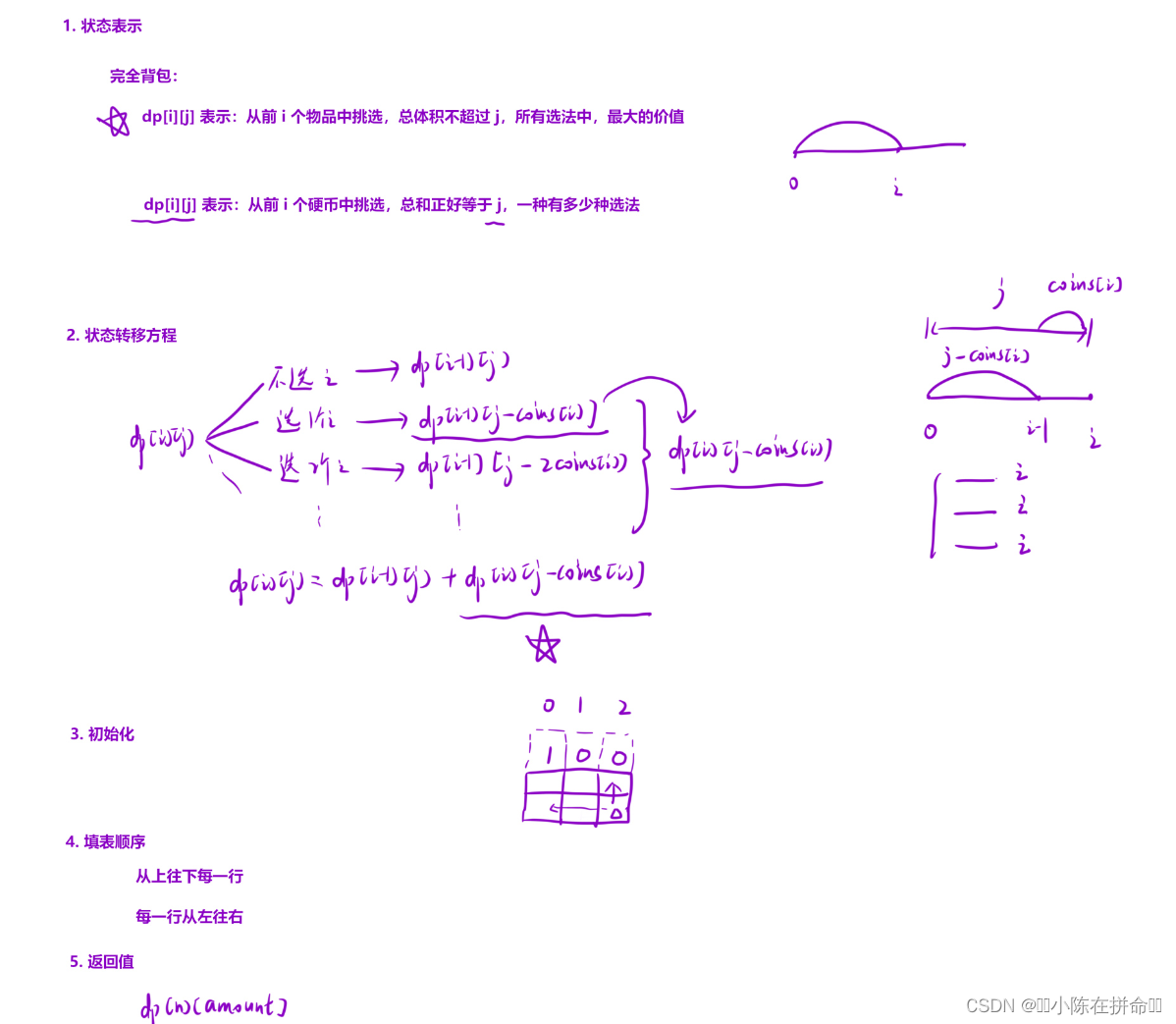
public:int change(int amount, vector<int>& coins) {//dp[i][j]表示从前i个硬币选,正好可以凑成总金额的硬币组合数//如果i不选 dp[i][j]+=dp[i-1][j]//如果i选1个 dp[i][j]+=dp[i-1][j-coins[i-1]]//dp[i][j]+=dp[i-1][j-coins[i-1]]+=dp[i-1][j-2coins[i-1]]……//dp[i][j]+=dp[i][j-coins[i-1]]int n=coins.size();//分析初始化 当j=0 都是一种选法 当i=0时 无论如何凑不出j 状态无效vector<vector<int>> dp(n+1,vector<int>(amount+1));dp[0][0]=1;for(int i=1;i<=n;++i)for(int j=0;j<=amount;++j) //不会越界,可以从0开始{dp[i][j]+=dp[i-1][j];if(j>=coins[i-1]) dp[i][j]+=dp[i][j-coins[i-1]];}return dp[n][amount];}
};滚动数组做优化:
class Solution {
public:int change(int amount, vector<int>& coins) {//dp[i][j]表示从前i个硬币选,正好可以凑成总金额的硬币组合数//如果i不选 dp[i][j]+=dp[i-1][j]//如果i选1个 dp[i][j]+=dp[i-1][j-coins[i-1]]//dp[i][j]+=dp[i-1][j-coins[i-1]]+=dp[i-1][j-2coins[i-1]]……//dp[i][j]+=dp[i][j-coins[i-1]]int n=coins.size();//分析初始化 当j=0 都是一种选法 当i=0时 无论如何凑不出j 状态无效vector<int> dp(amount+1);dp[0]=1;for(int i=1;i<=n;++i)for(int j=coins[i-1];j<=amount;++j) //不会越界,可以从0开始dp[j]+=dp[j-coins[i-1]]; //+= 0不会影响填表return dp[amount];}
};四、完全平方数
. - 力扣(LeetCode)

class Solution {
public:
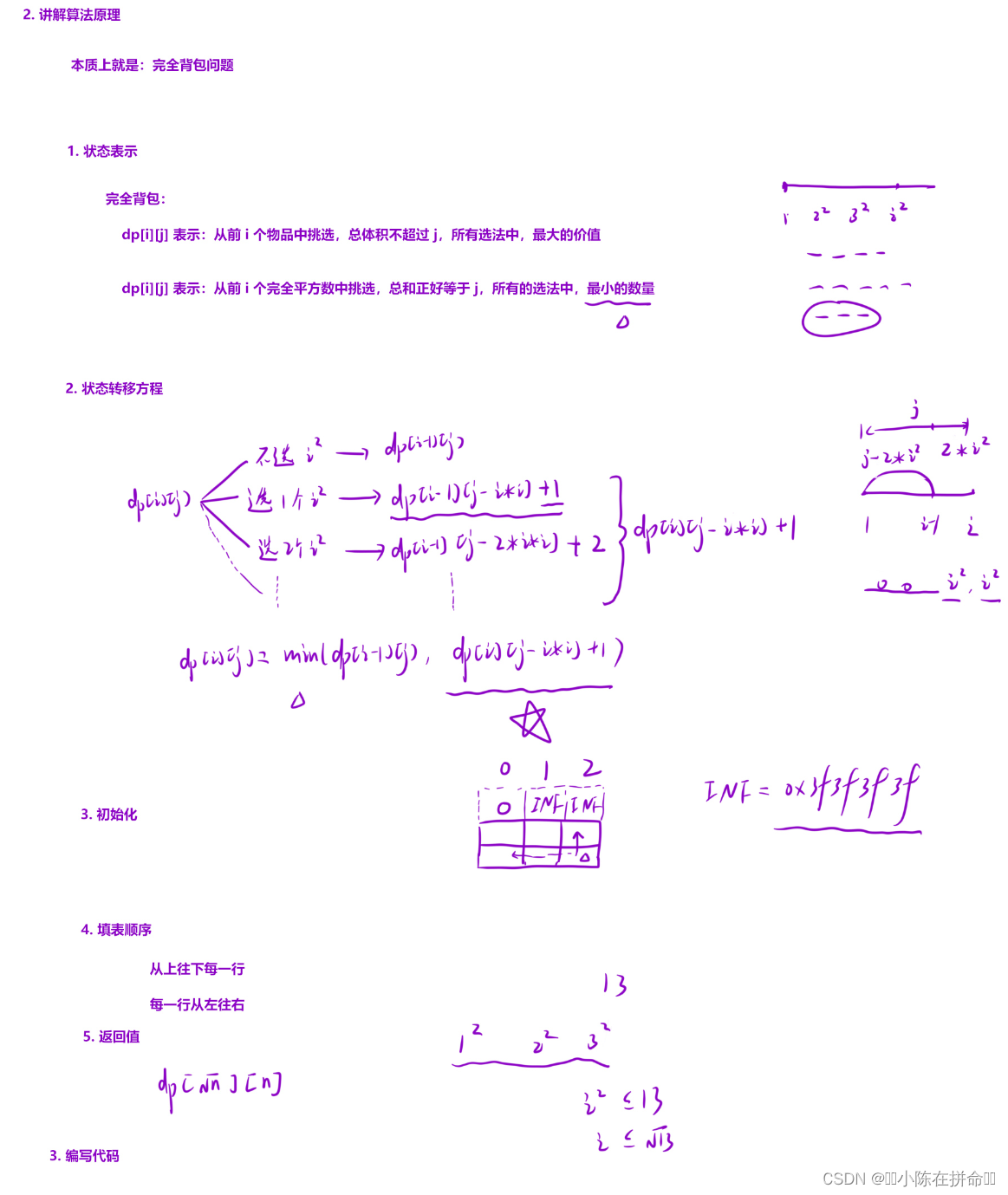
//不能用贪心策略 比如说1 4 9 组成12 444比9111好int numSquares(int n) {//1 4 9 16 25……//dp[i][j]表示从前i个数选,刚好为j的最少数量const int INF=0x3f3f3f3f;int m=sqrt(n);vector<int> dp(n+1,INF);//i=0的时候 不可能凑成j j=0时 i取1dp[0]=0;for(int i=1;i<=m;++i)for(int j=i*i;j<=n;++j)dp[j]=min(dp[j],dp[j-i*i]+1);return dp[n]; //一定能选得到,因为1是平方数 所以必然能凑出来}
};五、数位成本和为目标值的最大数字(经典dp还原)
. - 力扣(LeetCode)


class Solution {
public:string largestNumber(vector<int>& nums, int t) {//考虑数值长度问题,每个数字有相应成本,且长度均为1 //有若干物品,求给定费用下所能选择的最大价值 (完全背包)//得到的就是最大位数 然后从后往前想办法还原回来vector<int> dp(t+1,-0x3f3f3f3f);//会有不存在的状态//dp[i][j]表示前i个数选择 正好为j的最大选择数目dp[0]=1;for(int i=1;i<=9;++i)for(int j=nums[i-1];j<=t;++j)dp[j]=max(dp[j],dp[j-nums[i-1]]+1);//此时 dp[t]里存的就是选择的最大位数 然后要想办法进行还原if(dp[t]<0) return "0";string ret;//开始还原 从后往前还原for(int i=9;i>=1;--i){int u=nums[i-1];while(t>=u&&dp[t]==dp[t-u]+1)//说明选到这个数了{ret+=to_string(i);t-=u;}}return ret;}
};六、获得分数的方法数(多重背包)
. - 力扣(LeetCode)

该种类型题的具体分析请看第7题!!
class Solution {
public:const int MOD=1e9+7;int waysToReachTarget(int target, vector<vector<int>>& types) {//dp[i][j]表示从前i个数选 恰好分数为j的方案数 选择方式是types[1] //如果不选这个数 dp[i-1][j]//如果选 1个 dp[i-1][j-p[0]] //如果选2个 dp[i-1][j-2p[0]]int n=types.size();vector<vector<int>> dp(n+1,vector<int>(target+1));//初始化当i为0时 dp[0][0]=1;for(int i=1;i<=n;++i){int count=types[i-1][0],mark=types[i-1][1]; //count表示这道题的题数(选择次数) mark表示这道题的分数for(int j=0;j<=target;++j){dp[i][j]=dp[i-1][j];for(int k=1;k<=count;++k){if(j>=k*mark) dp[i][j]=(dp[i][j]+dp[i-1][j-k*mark])%MOD;}}}return dp[n][target];}
};滚动数组优化
class Solution {
public:const int MOD=1e9+7;int waysToReachTarget(int target, vector<vector<int>>& types) {//dp[i][j]表示从前i个数选 恰好分数为j的方案数 选择方式是types[1] //如果不选这个数 dp[i-1][j]//如果选 1个 dp[i-1][j-p[0]] //如果选2个 dp[i-1][j-2p[0]]vector<int> dp(target+1);//初始化当i为0时 dp[0]=1;for(auto&p:types){int count=p[0],mark=p[1]; //count表示这道题的题数(选择次数) mark表示这道题的分数 //会用到上一层的状态,所以滚动数组应该要从后往前for(int j=target;j>=0;--j){count=min(count,j/mark);for(int k=1;k<=count;++k)dp[j]=(dp[j]+dp[j-k*mark])%MOD;}}return dp[target];}
};
进阶优化:
class Solution {
public:const int MOD=1e9+7;int waysToReachTarget(int target, vector<vector<int>>& types) {//dp[i][j]表示从前i个数选 恰好分数为j的方案数 选择方式是types[1] //如果不选这个数 dp[i-1][j]//如果选 1个 dp[i-1][j-p[0]] //如果选2个 dp[i-1][j-2p[0]]//dp[i][j]+=dp[i-1][j-p[0]]……//dp[i][j-p[0]+=dp[i-1]][j-]vector<int> dp(target+1);//初始化当i为0时 dp[0]=1;for(auto&p:types){int count=p[0],mark=p[1]; //count表示这道题的题数(选择次数) mark表示这道题的分数 //会用到上一层的状态,所以滚动数组应该要从后往前for(int j=mark;j<=target;++j)dp[j]=(dp[j]+dp[j-mark])%MOD;for(int j=target;j>=(count+1)*mark;--j)dp[j] = (dp[j] - dp[j - mark*(count + 1)] + MOD) % MOD; // 两个同余前缀和的差//防止搞出负数}return dp[target];}
};
七、带和限制的子多重集合的数目(经典多重背包模版题)
. - 力扣(LeetCode)

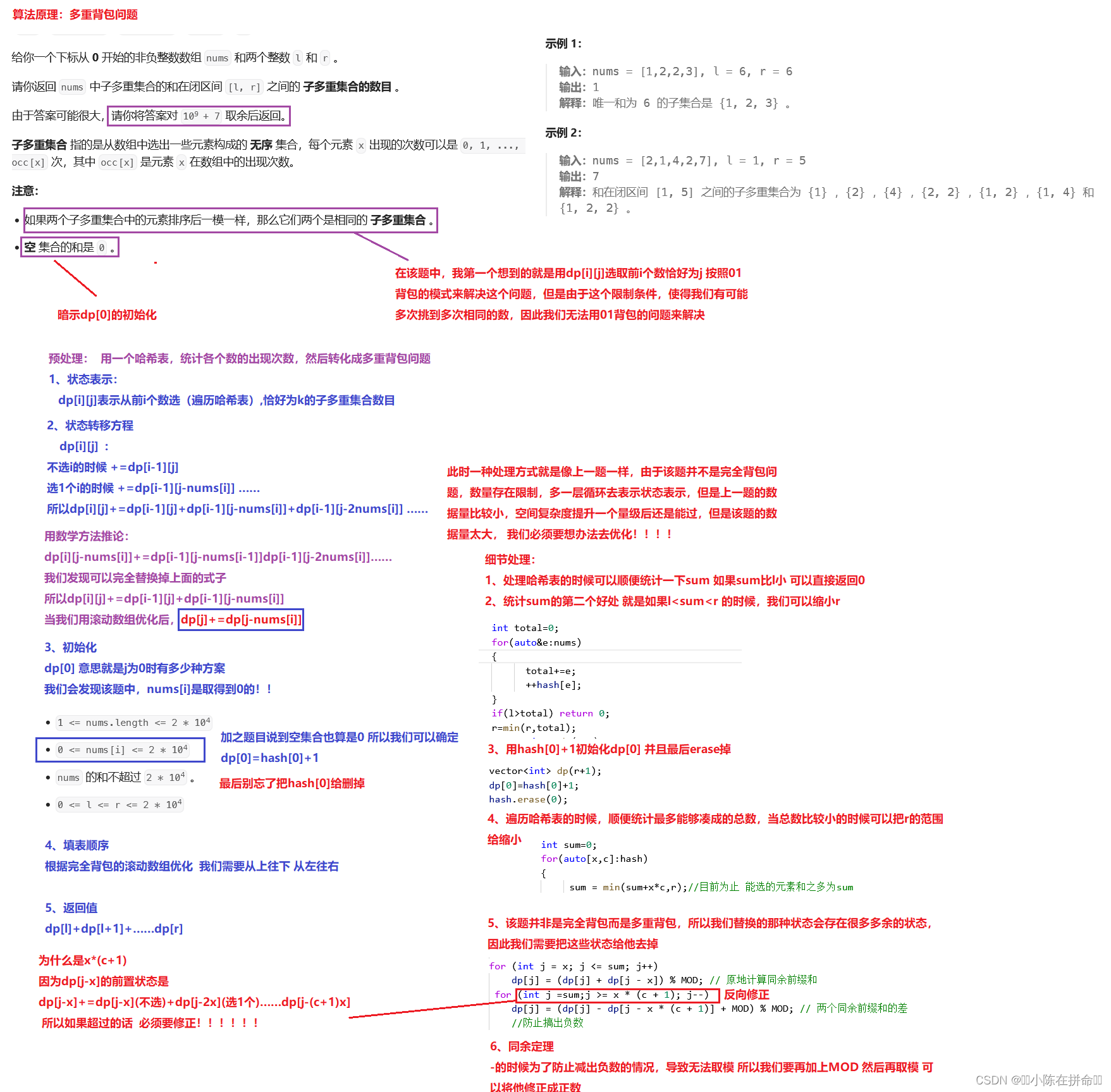
直接做滚动数组优化:
class Solution {
public:const int MOD=1e9+7;int countSubMultisets(vector<int>& nums, int l, int r) {//01背包 每个数选或者不选 限制范围是l-r//dp[i][j]表示从前i个数选 凑成和恰好为j//但是需要一个哈希表来帮助我们知道每个数究竟可以选多少次unordered_map<int,int> hash;int total=0;for(auto&e:nums) {total+=e;++hash[e];}if(l>total) return 0;r=min(r,total);vector<int> dp(r+1);//初始化 i=0时 无数可选dp[0]=hash[0]+1;hash.erase(0);int t=0;for(auto[x,c]:hash) //x是数 c是他的限制次数for(int j=r;j>=x;--j){c=min(c,j/x);for(int k=1;k<=c;++k) //费时间 想办法用新的状态dp[j]=(dp[j]+dp[j-k*x])%MOD; }int sum=0;for(int j=l;j<=r;++j)sum=(sum+dp[j])%MOD;return sum;}
};
我们会发现由于数据量太大,用循环会超时,因此我们在这里不能用k那一层循环!!得换个方式
class Solution {
public:const int MOD=1e9+7;int countSubMultisets(vector<int>& nums, int l, int r) {//01背包 每个数选或者不选 限制范围是l-r//dp[i][j]表示从前i个数选 凑成和恰好为j//但是需要一个哈希表来帮助我们知道每个数究竟可以选多少次//类比完全背包的状态 dp[]unordered_map<int,int> hash;int total=0;for(auto&e:nums) {total+=e;++hash[e];}if(l>total) return 0;r=min(r,total);vector<int> dp(r+1);dp[0]=hash[0]+1;hash.erase(0);// dp[i][j]+= dp[i-1][j-x]+dp[i-1][j-2*x]……// dp[i][j-x]+=dp[i-1][j-2x]+dp[i-1][j-3x]……int sum=0;for(auto[x,c]:hash){sum = min(sum+x*c,r);//目前为止 能选的元素和之多为sum for (int j = x; j <= sum; j++)dp[j] = (dp[j] + dp[j - x]) % MOD; // 原地计算同余前缀和for (int j =sum;j >= x * (c + 1); j--)dp[j] = (dp[j] - dp[j - x * (c + 1)] + MOD) % MOD; // 两个同余前缀和的差//防止搞出负数}int ret=0;for(int j=l;j<=r;++j)ret=(ret+dp[j])%MOD;return ret;}
};

相关文章:

DP:完全背包+多重背包问题
完全背包和01背包的区别就是:可以多次选 一、完全背包(模版) 【模板】完全背包_牛客题霸_牛客网 #include <iostream> #include<string.h> using namespace std; const int N1001; int n,V,w[N],v[N],dp[N][N]; //dp[i][j]表示…...

购物返利系统的安全性:防范欺诈与数据保护
购物返利系统的安全性:防范欺诈与数据保护 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 购物返利系统作为一种电子商务模式,通过向消…...
从WebM到MP3:利用Python和wxPython提取音乐的魔法
前言 有没有遇到过这样的问题:你有一个包含多首歌曲的WebM视频文件,但你只想提取其中的每一首歌曲,并将它们保存为单独的MP3文件?这听起来可能有些复杂,但借助Python和几个强大的库,这个任务变得异常简单。…...

图片转pdf,图片转pdf在线转换,在线图片转pdf
图片转PDF,听起来似乎是一个简单的操作,但实际上,它涉及到许多细节和技巧。有时候我们需要将图片转换为PDF格式,以便于分享、打印或保存。那么,如何将图片转换成PDF呢?接下来,我将为您详细介绍几…...

SpringBoot3使用Swagger3
SpringBoot3使用Swagger3 项目中的后端接口进行简单的前端展示一、依赖引入二、快速启动1.在application.yml中配置2.或者properties文件,则配置3.启动项目访问swagger 三、使用注解标注接口Swagger配置文件Swagger 注解迁移举例五种常用ApiApiOperationApiImplicitParamApiMod…...
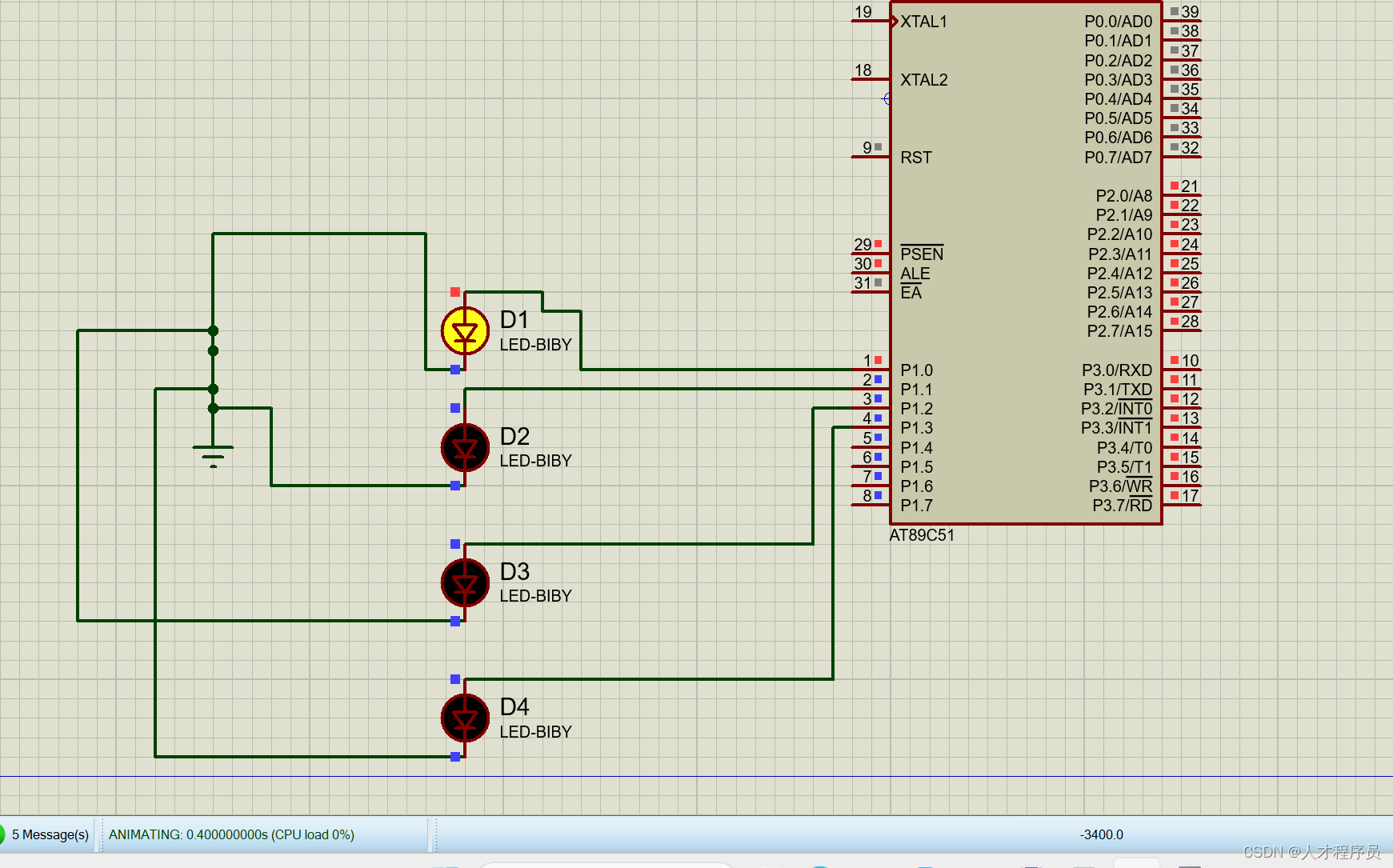
【51单片机基础教程】点亮led
文章目录 前言51单片机点亮LED的原理硬件部分软件部分51单片机的寄存器编程步骤proteus仿真点亮一个led 点亮多个ledproteus仿真代码 流水灯 总结 前言 单片机(Microcontroller Unit, MCU)是一种集成电路,广泛应用于各种电子产品中。作为嵌入…...

Docker之overlay2的迁移
原因 docker默认将文件及其容器放置在了系统盘的挂载区内,如果长期使用会发现系统挂载区被overlay2挤爆了,因此在一开始我们将其迁移在大容量外挂磁盘上,就可以避免系统盘被挤爆,放心使用. 具体操作 # 停止容器 systemctl stop docker# 修改容器配置,…...

CentOS中的rename命令
目录 CentOS中的rename命令基本语法使用示例注意事项安装prename CentOS中的rename命令 在CentOS系统中,rename命令通常是指util-linux包中提供的版本,它用于批量重命名文件,但与Perl版本的rename命令相比,功能较为简单ÿ…...
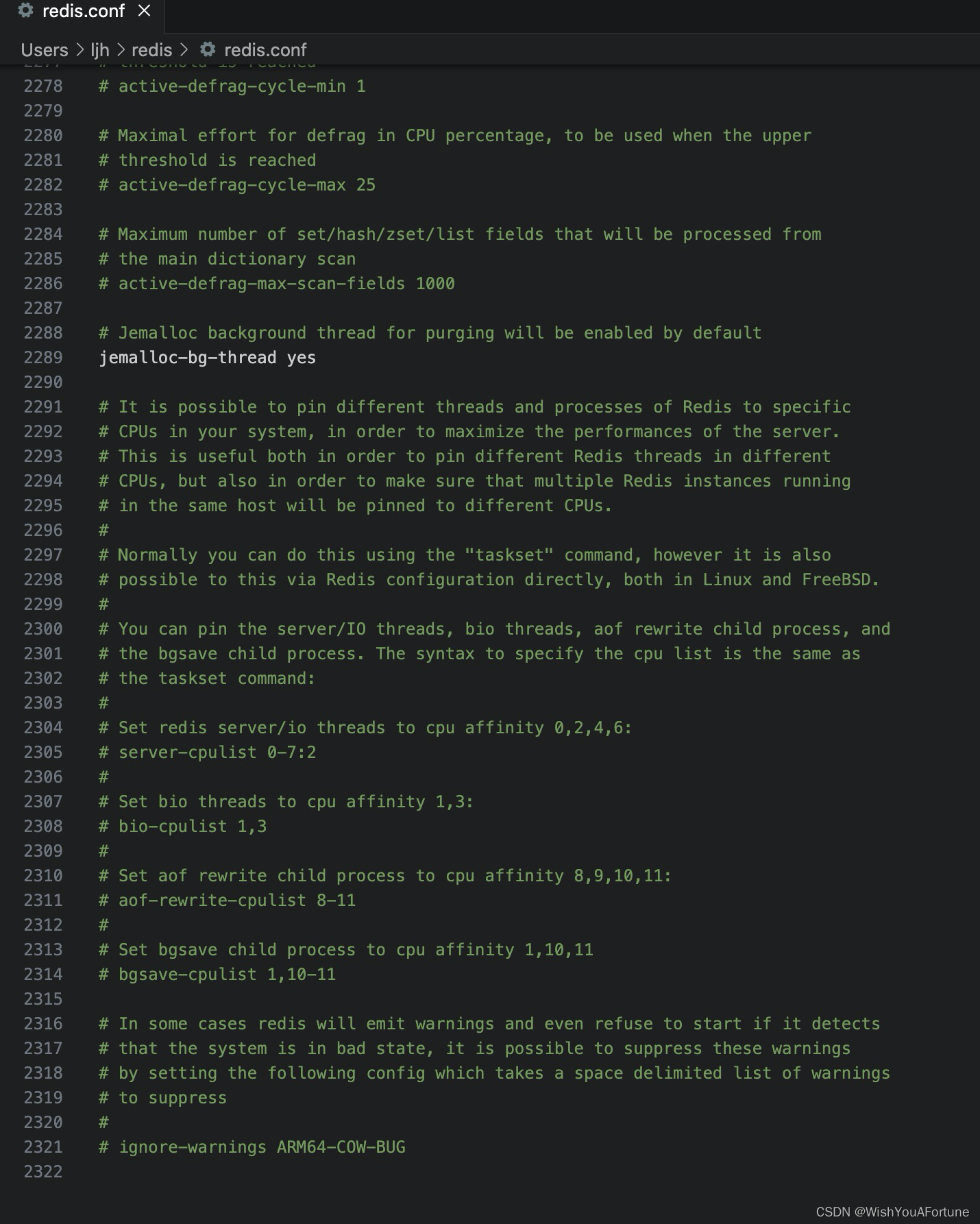
redis.conf 参数详解,方便进行性能优化配置
以下是redis.conf中一些常见参数的详细说明: daemonize:是否以后台进程运行,默认为no; pidfile:如以后台进程运行,则需指定一个pid,默认为/var/run/redis.pid;bind:绑定主…...

微信小程序登录流程详情及Java代码
一、流程图 说明: 调用 wx.login() 获取 临时登录凭证code ,并回传到开发者服务器。 调用 auth.code2Session 接口,换取 用户唯一标识 OpenID 和 会话密钥 session_key。 获取手机号,调用wx.getPhoneNumber() ,获取加密…...
c++qt合并两张灰度图像
需求:将两张尺寸相同的灰度图像进行合并,合并后的图像,每个像素点灰度值为两张原图对应像素点灰度值之和。若超过255,则最大为255。 方法一: 将图像读取为cv::Mat,再调用opencv的cv::add方法,进…...

Uniapp通过年月日时间转变星期格式
效果图 参靠微信小程序:日常记一记 代码 <view v-for"(d,index) in dataList" >{{getWeekDay(d.ctime)}} //时间格式:2024-06-21</view> js export default {data(){return {dataList:[],//时间数组}},onLoad() {this.loadList…...

如何编写和执行高效的测试计划
如何编写和执行高效的测试计划 1. 测试计划概述2. 测试阶段详解3. 测试计划模板4. 关键注意事项总结 1. 测试计划概述 测试计划是指导整个测试过程的重要文档,其中包含了测试策略、资源分配、进度安排以及风险评估等内容。 一个完善的测试计划应当包括以下几个主要…...

【MySQL连接器(Python)指南】03-MySQL连接器(Python)安装
文章目录 前言1. 从二进制发行版中安装连接器1.1 使用pip安装MySQL连接器1.2 使用MySQL Yum Repository安装1.3 使用Debian软件包安装连接器2. 从源代码发行版安装连接器2.1 在Windows上源码安装2.2 在类Unix系统上源码安装3. 验证连接器安装总结前言 MySQL连接器(Python),用于…...

Spring Boot组件化与参数校验
Spring Boot组件化与参数校验 Spring Boot版本选择 2.3.x版本 2.6.x版本 Spring Boot核心思想 约定大于配置,简化繁琐的配置 Spring Boot自动配置原理 SpringBootApplication: Spring Boot应用标注在某个类上说明这个类是SpringBoot的主配置类,Spr…...

实现可扩展的电商返利平台:技术选型与挑战
实现可扩展的电商返利平台:技术选型与挑战 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 在当今数字化和电商兴盛的时代,返利平台成为…...

从0开始C++(三):构造函数与析构函数详解
目录 构造函数 构造函数的基本使用 构造函数也支持函数重载 构造函数也支持函数参数默认值 构造初始化列表 拷贝构造函数 浅拷贝和深拷贝 析构函数 总结 练习一下ヽ( ̄▽ ̄)ノ 构造函数 构造函数的基本使用 构造函数是一种特殊的成…...

行车记录仪文件夹“0字节”现象解析与恢复策略
一、行车记录仪文件夹“0字节”现象描述 行车记录仪作为现代驾驶中的必备设备,其储存的视频数据对于事故记录和取证至关重要。然而,有时车主们可能会遇到这样一个问题:行车记录仪的某个文件夹内的文件突然变成了0字节大小,无法正…...

呼叫中心系统的功能都有哪些?okcc呼叫中心pscc磐石云呼叫系统部署
当前电话营销普及到各行各业,方便快捷成了大部分企业在宣传自己公司的产品时必用的一种营销方式,但是电话营销在管理上也存在许多问题。例如:销售员与客户沟通前,未能详细了解客户的资料;多名销售员重复拨打同一个客户…...

2024.06.08校招 实习 内推 面经
绿*泡*泡VX: neituijunsir 交流*裙 ,内推/实习/校招汇总表格 1、提前批 | 中电锦江2025届提前批招聘 提前批 | 中电锦江2025届提前批招聘 2、实习 | 国电电力2025届暑期实习生计划启动! 实习 | 国电电力2025届暑期实习生计划启动&#x…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...
