【2024最新华为OD-C/D卷试题汇总】[支持在线评测] 5G基站光纤连接问题(200分) - 三语言AC题解(Python/Java/Cpp)
🍭 大家好这里是清隆学长 ,一枚热爱算法的程序员
✨ 本系列打算持续跟新华为OD-C/D卷的三语言AC题解
💻 ACM银牌🥈| 多次AK大厂笔试 | 编程一对一辅导
👏 感谢大家的订阅➕ 和 喜欢💗
📎在线评测链接
https://app5938.acapp.acwing.com.cn/contest/2/problem/OD1072
🌍 评测功能需要 ⇒ 订阅专栏 ⇐ 后私信联系清隆解锁~
🍓OJ题目截图
文章目录
- 📎在线评测链接
- 🍓OJ题目截图
- 🍿 5G基站光纤连接问题
- 问题描述
- 输入格式
- 输出格式
- 样例输入
- 样例 1
- 样例 2
- 样例 3
- 样例输出
- 样例 1 输出
- 样例 2 输出
- 样例 3 输出
- 样例解释
- 样例 1 解释
- 样例 2 解释
- 样例 3 解释
- 数据范围
- 题解
- 参考代码
🍿 5G基站光纤连接问题
问题描述
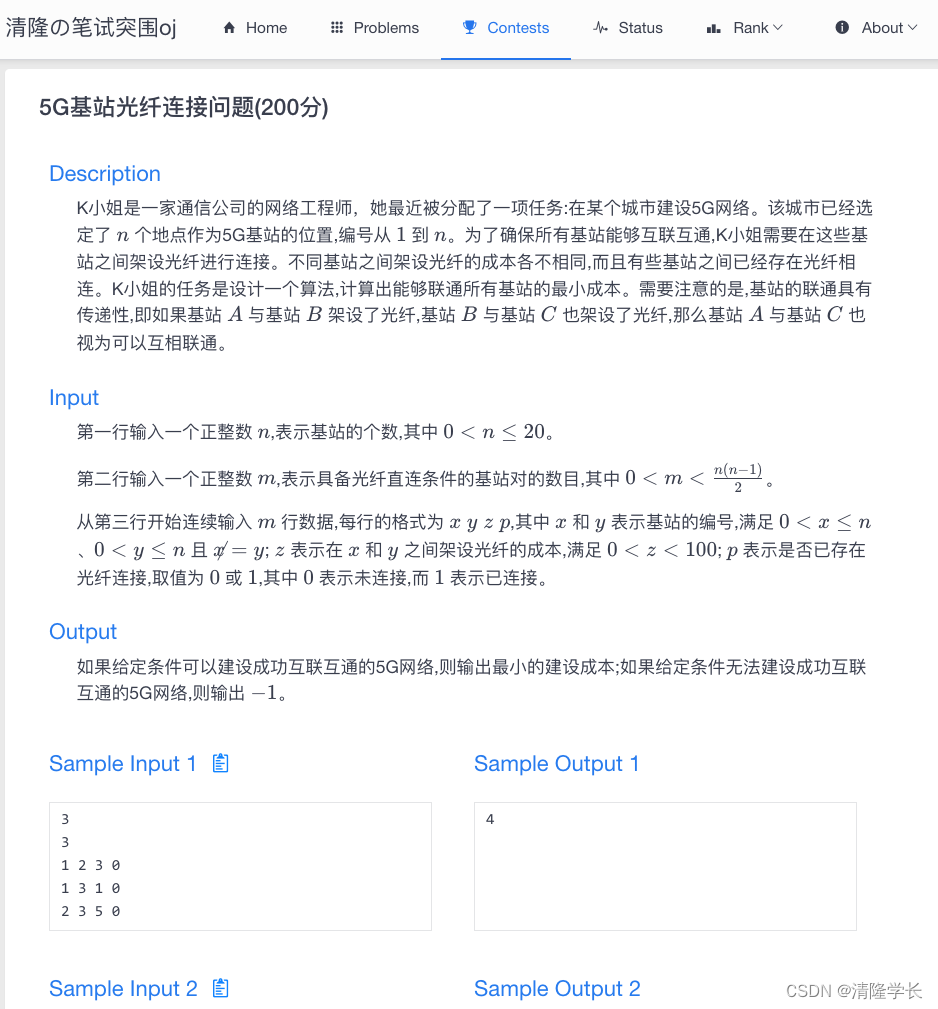
K小姐是一家通信公司的网络工程师,她最近被分配了一项任务:在某个城市建设5G网络。该城市已经选定了 n n n 个地点作为5G基站的位置,编号从 1 1 1 到 n n n。为了确保所有基站能够互联互通,K小姐需要在这些基站之间架设光纤进行连接。不同基站之间架设光纤的成本各不相同,而且有些基站之间已经存在光纤相连。K小姐的任务是设计一个算法,计算出能够联通所有基站的最小成本。需要注意的是,基站的联通具有传递性,即如果基站 A A A 与基站 B B B 架设了光纤,基站 B B B 与基站 C C C 也架设了光纤,那么基站 A A A 与基站 C C C 也视为可以互相联通。
输入格式
第一行输入一个正整数 n n n,表示基站的个数,其中 0 < n ≤ 20 0 < n \leq 20 0<n≤20。
第二行输入一个正整数 m m m,表示具备光纤直连条件的基站对的数目,其中 0 < m < n ( n − 1 ) 2 0 < m < \frac{n(n-1)}{2} 0<m<2n(n−1)。
从第三行开始连续输入 m m m 行数据,每行的格式为 x y z p x\ y\ z\ p x y z p,其中 x x x 和 y y y 表示基站的编号,满足 0 < x ≤ n 0 < x \leq n 0<x≤n、 0 < y ≤ n 0 < y \leq n 0<y≤n 且 x ≠ y x \neq y x=y; z z z 表示在 x x x 和 y y y 之间架设光纤的成本,满足 0 < z < 100 0 < z < 100 0<z<100; p p p 表示是否已存在光纤连接,取值为 0 0 0 或 1 1 1,其中 0 0 0 表示未连接,而 1 1 1 表示已连接。
输出格式
如果给定条件可以建设成功互联互通的5G网络,则输出最小的建设成本;如果给定条件无法建设成功互联互通的5G网络,则输出 − 1 -1 −1。
样例输入
样例 1
3
3
1 2 3 0
1 3 1 0
2 3 5 0
样例 2
3
1
1 2 5 0
样例 3
3
3
1 2 3 0
1 3 1 0
2 3 5 1
样例输出
样例 1 输出
4
样例 2 输出
-1
样例 3 输出
1
样例解释
样例 1 解释
只需要在基站 1 1 1 和基站 2 2 2 之间,以及基站 2 2 2 和基站 3 3 3 之间铺设光纤,其成本为 3 + 1 = 4 3 + 1 = 4 3+1=4。
样例 2 解释
基站 3 3 3 无法与其他基站连接,因此无法建设成功互联互通的5G网络,输出 − 1 -1 −1。
样例 3 解释
基站 2 2 2 和基站 3 3 3 已有光纤相连,只需要在基站 1 1 1 和基站 3 3 3 之间铺设光纤,其成本为 1 1 1。
数据范围
- 0 < n ≤ 20 0 < n \leq 20 0<n≤20
- 0 < m < n ( n − 1 ) 2 0 < m < \frac{n(n-1)}{2} 0<m<2n(n−1)
- 0 < x , y ≤ n 0 < x, y \leq n 0<x,y≤n, x ≠ y x \neq y x=y
- 0 < z < 100 0 < z < 100 0<z<100
- p ∈ { 0 , 1 } p \in \{0, 1\} p∈{0,1}
题解
这是一个经典的最小生成树问题,可以使用 Kruskal 算法或 Prim 算法求解。这里我们采用 Kruskal 来解决,首先将所有已经存在光纤连接的基站对进行合并,然后按照架设光纤的成本从小到大排序,依次尝试连接未连通的基站对。如果连接后不会形成环路,则将该条边加入最小生成树中。当所有基站都被连通后,最小生成树的边权之和就是最小的建设成本。
如果最终无法将所有基站连通,则输出 − 1 -1 −1。
参考代码
- Python
# 并查集
class UnionFind:def __init__(self, n):self.parent = list(range(n + 1))self.rank = [0] * (n + 1)def find(self, x):if self.parent[x] != x:self.parent[x] = self.find(self.parent[x])return self.parent[x]def union(self, x, y):px, py = self.find(x), self.find(y)if px == py:returnif self.rank[px] < self.rank[py]:self.parent[px] = pyelif self.rank[px] > self.rank[py]:self.parent[py] = pxelse:self.parent[py] = pxself.rank[px] += 1n = int(input())
m = int(input())
uf = UnionFind(n)
edges = []for _ in range(m):x, y, w, p = map(int, input().split())if p == 1:uf.union(x, y)else:edges.append((w, x, y))edges.sort()
cost = 0
for w, x, y in edges:if uf.find(x) != uf.find(y):uf.union(x, y)cost += wif len(set(uf.find(i) for i in range(1, n + 1))) == 1:print(cost)
else:print(-1)
- Java
import java.util.*;class UnionFind {int[] parent;int[] rank;public UnionFind(int n) {parent = new int[n + 1];rank = new int[n + 1];for (int i = 0; i <= n; i++) {parent[i] = i;}}public int find(int x) {if (parent[x] != x) {parent[x] = find(parent[x]);}return parent[x];}public void union(int x, int y) {int px = find(x);int py = find(y);if (px == py) {return;}if (rank[px] < rank[py]) {parent[px] = py;} else if (rank[px] > rank[py]) {parent[py] = px;} else {parent[py] = px;rank[px]++;}}
}public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();int m = sc.nextInt();UnionFind uf = new UnionFind(n);List<int[]> edges = new ArrayList<>();for (int i = 0; i < m; i++) {int x = sc.nextInt();int y = sc.nextInt();int w = sc.nextInt();int p = sc.nextInt();if (p == 1) {uf.union(x, y);} else {edges.add(new int[]{w, x, y});}}edges.sort((a, b) -> a[0] - b[0]);int cost = 0;for (int[] edge : edges) {int w = edge[0];int x = edge[1];int y = edge[2];if (uf.find(x) != uf.find(y)) {uf.union(x, y);cost += w;}}Set<Integer> roots = new HashSet<>();for (int i = 1; i <= n; i++) {roots.add(uf.find(i));}if (roots.size() == 1) {System.out.println(cost);} else {System.out.println(-1);}}
}
- Cpp
#include <iostream>
#include <vector>
#include <algorithm>using namespace std;class UnionFind {
private:vector<int> parent;vector<int> rank;public:UnionFind(int n) {parent.resize(n + 1);rank.resize(n + 1, 0);for (int i = 0; i <= n; i++) {parent[i] = i;}}int find(int x) {if (parent[x] != x) {parent[x] = find(parent[x]);}return parent[x];}void merge(int x, int y) {int px = find(x);int py = find(y);if (px == py) {return;}if (rank[px] < rank[py]) {parent[px] = py;} else if (rank[px] > rank[py]) {parent[py] = px;} else {parent[py] = px;rank[px]++;}}
};int main() {int n, m;cin >> n >> m;UnionFind uf(n);vector<vector<int>> edges;for (int i = 0; i < m; i++) {int x, y, w, p;cin >> x >> y >> w >> p;if (p == 1) {uf.merge(x, y);} else {edges.push_back({w, x, y});}}sort(edges.begin(), edges.end());int cost = 0;for (auto edge : edges) {int w = edge[0];int x = edge[1];int y = edge[2];if (uf.find(x) != uf.find(y)) {uf.merge(x, y);cost += w;}}bool success = true;int root = uf.find(1);for (int i = 2; i <= n; i++) {if (uf.find(i) != root) {success = false;break;}}if (success) {cout << cost << endl;} else {cout << -1 << endl;}return 0;
}
相关文章:

【2024最新华为OD-C/D卷试题汇总】[支持在线评测] 5G基站光纤连接问题(200分) - 三语言AC题解(Python/Java/Cpp)
🍭 大家好这里是清隆学长 ,一枚热爱算法的程序员 ✨ 本系列打算持续跟新华为OD-C/D卷的三语言AC题解 💻 ACM银牌🥈| 多次AK大厂笔试 | 编程一对一辅导 👏 感谢大家的订阅➕ 和 喜欢💗 …...
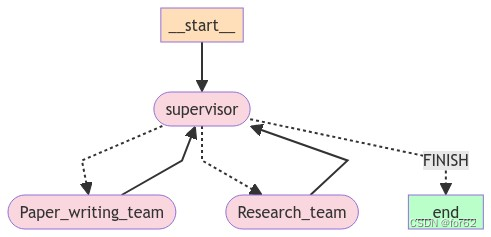
分层Agent
分层Teams 分层Agent创建tool研究团队工具文档编写团队工具 通用能力定义Agent团队研究团队文档编写团队 添加图层 分层Agent 在前面的示例(Agent管理)中,我们引入了单个管理节点的概念,用于在不同工作节点之间路由工作。 但是&a…...

OS复习笔记ch11-1
外围设备的管理和磁盘调度 外围设备 从CPU的角度来看,外设有几个比较重要的I/O接口(interfaces) 状态reg:向CPU报告设备的状态(忙碌/空闲)命令reg:接收CPU命令,存储 CPU 需要执行的…...

Docker Compose 使用
一、简介 Docker Compose 是一个工具,用于定义和运行多容器 Docker 应用程序。它允许用户使用 YAML 文件来配置应用程序需要的所有服务,然后使用一个命令来从 YAML 文件配置中创建并启动所有服务。其主要目的是为了简化了多容器 Docker 应用程序的部署和…...

KEIL5.39 5.40 fromelf 不能生成HEX bug
使用AC6 编译,只要勾选了生成HEX。 结果报如下错误 暂时没有好的解决办法 1.替换法 2.在编译完后用命令生成HEX...

mongosh 和mongo 命令行连接MongoDB
Mongoshell MongoDB的Shell工具mongosh是一个全功能的JavaScript和Node.js的14.x REPL与MongoDB的部署交互环境。我们通过它可以直接对数据库进行查询和操作。这个工具是需要在安装玩MongoDB后单独安装的。 与传统的mongo方式连接MongoDB更加丰富。 官网 https://www.mongodb.…...

DOM 改变节点
DOM 改变节点 文档对象模型(DOM)是 HTML 和 XML 文档的编程接口。它提供了对文档的结构化表示,并定义了一种方式,允许程序和脚本动态地访问和更新文档的内容、结构和样式。在网页开发中,DOM 操作是核心技能之一&#…...

【面试题分享】重现 string.h 库常用的函数
文章目录 【面试题分享】重现 string.h 库常用的函数一、字符串复制1. strcpy(复制字符串直到遇到 null 终止符)2. strncpy(复制固定长度的字符串) 二、字符串连接1. strcat(将一个字符串连接到另一个字符串的末尾&…...
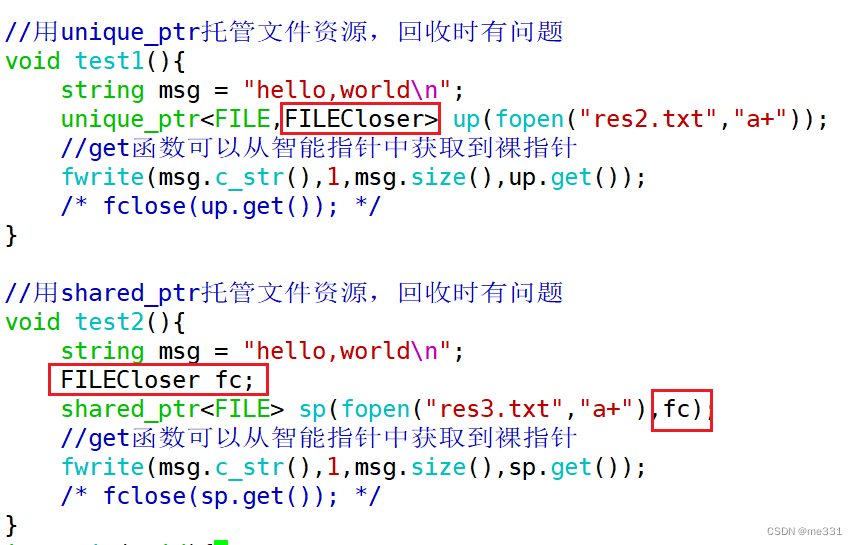
6.21 移动语义与智能指针
//先构造,再拷贝构造//利用"hello"这个字符串创建了一个临时对象//并复制给了s3//这一步实际上new了两次String s3 "hello"; 背景需求: 这个隐式创建的字符串出了该行就直接销毁掉,效率比较低 可以让_pstr指向这个空间…...

Kimi还能对学术论文进行润色?我来教你!
学境思源,一键生成论文初稿: AcademicIdeas - 学境思源AI论文写作 一、引言 在学术界,论文的质量往往决定了研究的可信度和影响力。Kimi作为一款人工智能助手,可以为学术论文的润色提供有效的帮助。本文将详细介绍如何利用Kimi进…...

智汇云舟成为中煤集团中煤智能创新联盟成员单位
6月21日,第八届世界智能产业博览会平行会议暨中煤智能创新联盟交流会在天津水游城丽筠酒店顺利举行。智汇云舟受邀参与,并由中国中煤能源集团授予荣誉证书,正式成为中煤智能创新联盟成员单位。会议上,清华大学、中国矿业大学&…...
【文心智能体大赛】迎接属于你的休闲娱乐导师!
迎接属于你的休闲娱乐导师! 前言创建智能体发布智能体最后结语 前言 文心智能体平台AgentBuilder 是百度推出的基于文心大模型的智能体(Agent)平台,支持广大开发者根据自身行业领域、应用场景,选取不同类型的开发方式&…...

AI:音乐创作的未来还是毁灭的序曲?
AI:音乐创作的未来还是毁灭的序曲? 随着人工智能(AI)技术的飞速发展,它已经渗透到了我们生活的方方面面,包括音乐领域。然而,AI在音乐创作中的角色引发了广泛的讨论和争议。一些人认为AI为音乐…...

如何通过AI进行智能日志异常检测
智能日志异常检测是一种利用人工智能(AI)技术来自动识别日志数据中异常模式或行为的方法。传统日志监控依赖于预定义规则,而智能日志异常检测可以适应不同的日志模式和异常类型,提高检测准确性和效率。下面是一个完整的步骤指南&a…...

C++ GPU编程(英伟达CUDA)
安装编译环境 https://developer.download.nvidia.com/compute/cuda/12.5.0/local_installers/cuda_12.5.0_555.85_windows.exe CMakeLists.txt cmake_minimum_required(VERSION 3.10)set(CMAKE_CXX_STANDARD 17) set(CMAKE_BUILD_TYPE Release) #set(CMAKE_CUDA_ARCHITECTUR…...
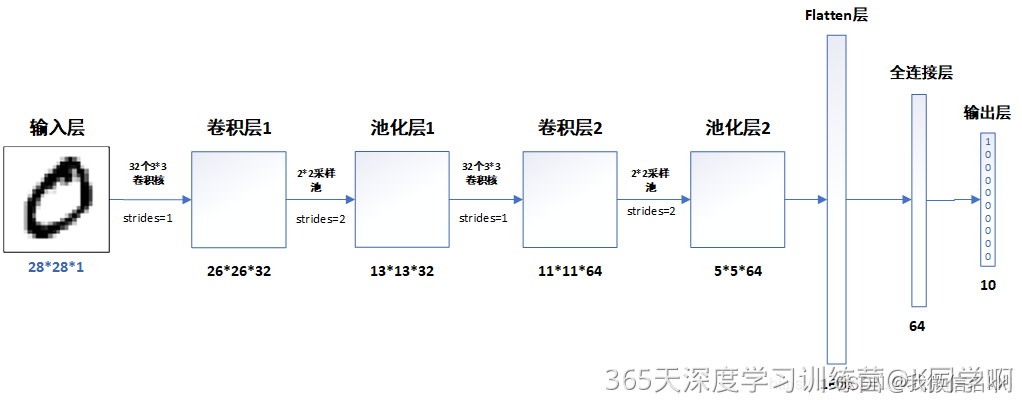
肾虚学习实验第T1周:实现mnist手写数字识别
>- **🍨 本文为[🔗365天深度学习训练营](https://mp.weixin.qq.com/s/0dvHCaOoFnW8SCp3JpzKxg) 中的学习记录博客** >- **🍖 原作者:[K同学啊](https://mtyjkh.blog.csdn.net/)** 目录 一、前言 作为一名研究牲࿰…...

Python | Leetcode Python题解之第162题寻找峰值
题目: 题解: class Solution:def findPeakElement(self, nums: List[int]) -> int:n len(nums)# 辅助函数,输入下标 i,返回 nums[i] 的值# 方便处理 nums[-1] 以及 nums[n] 的边界情况def get(i: int) -> int:if i -1 or…...
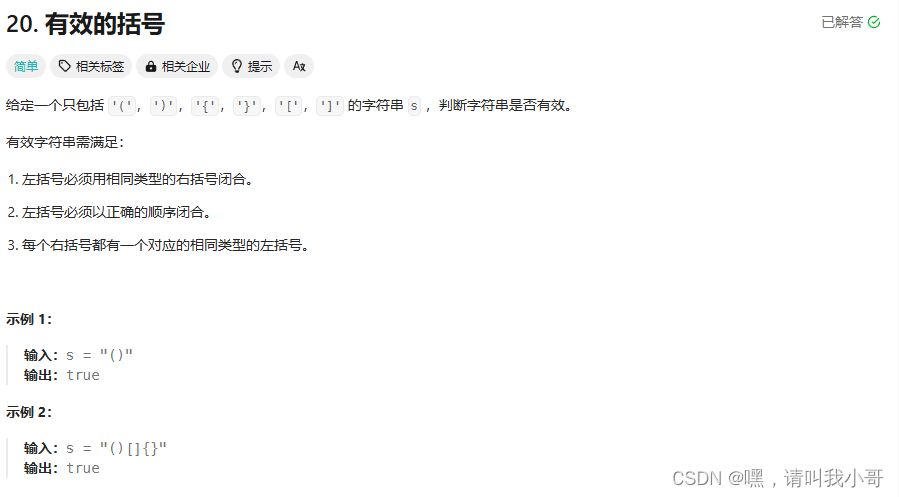
定个小目标之刷LeetCode热题(26)
这道题属于一道简单题,可以使用辅助栈法,代码如下所示 class Solution {public boolean isValid(String s) {if (s.isEmpty())return false;// 创建字符栈Stack<Character> stack new Stack<Character>();// 遍历字符串数组for (char c : …...
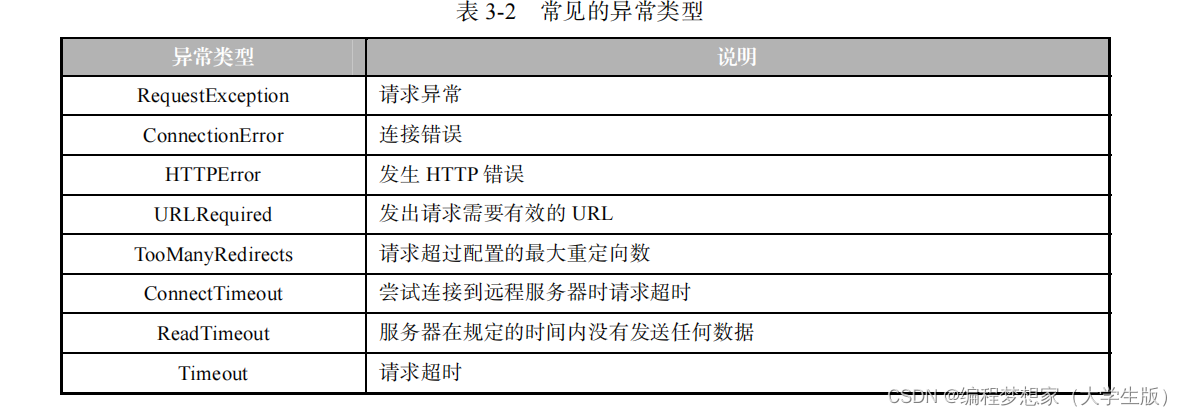
网络爬虫设置代理服务器
目录 1.获取代理 IP 2.设置代理 IP 3. 检测代理 IP 的有效性 4. 处理异常 如果希望在网络爬虫程序中使用代理服务器,就需要为网络爬虫程序设置代理服务器。 设置代理服务器一般分为获取代理 IP 、设置代理 IP 两步。接下来,分…...

3、matlab单目相机标定原理、流程及实验
1、单目相机标定流程及步骤 单目相机标定是通过确定相机的内部和外部参数,以便准确地在图像空间和物体空间之间建立映射关系。下面是单目相机标定的流程及步骤: 搜集标定图像:使用不同角度、距离和姿态拍摄一组标定图像,并确保标…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...
