202109-3 CCF 脉冲神经网络 66分题解 + 解题思路 + 解题过程
解题思路
根据题意,脉冲源的阈值大于随机数时,会向其所有出点发送脉冲
神经元当v>=30时,会向其所有出点发送脉冲,unordered_map <int, vector > ne; //存储神经元/脉冲源的所有出点集合vector
所有脉冲会有一定的延迟,所以使用unordered_map <int, unordered_map <int, double>> I; //存储神经元i的j时刻收到的所有脉冲和
暴力做法就是遍历每一时刻,每一时刻更新神经元和脉冲源,最后统计答案
解题过程
- 一开始用结构体实现,并且没有考虑到一个神经元/脉冲源可能会对多个神经元发出脉冲这个问题,直接按照题意纯模拟,得了16分。。
- 发现了一对多的情况,在结构体中加入了一个vector存储所有的出点,爆内存了,得了33分。。

- 由于每个神经元也不是每一时刻都会收到脉冲,所以稍微改了下,不采用数组存储,采用unorder_map存储,不爆内存了,TLE了。。66分。。

66分暴力版本代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#include <unordered_map>using namespace std;const int N = 1010;static unsigned long nt = 1;/* RAND_MAX assumed to be 32767 */
int myrand(void) {nt = nt * 1103515245 + 12345;return((unsigned)(nt/65536) % 32768);
}struct node
{int id;double w;int D;
};double v[N], u[N], a[N], b[N], c[N], d[N];
unordered_map <int, vector <node>> ne;
unordered_map <int, unordered_map <int, double>> I;
int sum[N];
int r[2 * N];int main()
{int n, s, p, t;cin >> n >> s >> p >> t;double dt;cin >> dt;int rn;for (int i = 0; i < n; i += rn) //0 ~ n - 1神经元{cin >> rn;double vv, uu, aa, bb, cc, dd;cin >> vv >> uu >> aa >> bb >> cc >> dd;for (int j = i; j < i + rn; j ++){v[j] = vv;u[j] = uu;a[j] = aa;b[j] = bb;c[j] = cc;d[j] = dd;}}for (int i = n; i < n + p; i ++) //n ~ n + p - 1脉冲源{cin >> r[i];}for (int i = 0; i < s; i ++) //突触{int bn, ed;double w;int D;cin >> bn >> ed >> w >> D;struct node t = {ed, w, D};ne[bn].push_back(t);}for (int i = 1; i <= t; i ++) //遍历每一时刻{for (int j = 0; j < n; j ++) //更新神经元{double pv = v[j], pu = u[j];v[j] = pv + dt * (0.04 * pv * pv + 5.0 * pv + 140.0 - pu) + I[j][i];u[j] = pu + dt * a[j] * (b[j] * pv - pu);if (v[j] >= 30.0){v[j] = c[j];u[j] += d[j];sum[j] ++;for (auto x : ne[j]) //向所有出点释放脉冲{int id = x.id;double w = x.w;int D = x.D;I[id][i + D] += w;}}}for (int j = n; j < n + p; j ++) //脉冲源释放脉冲{int x = myrand();if (r[j] > x) //r大于随机值{for (auto x : ne[j]) //向所有出点释放脉冲{int id = x.id;double w = x.w;int D = x.D;I[id][i + D] += w;}}}}double r1 = v[0], r2 = v[0];int s1 = sum[0], s2 = sum[0];for (int i = 1; i < n; i ++) //得到答案{r1 = min(r1, v[i]);r2 = max(r2, v[i]);s1 = min(s1, sum[i]);s2 = max(s2, sum[i]);}printf("%.3lf %.3lf\n", r1, r2);cout << s1 << " " << s2;return 0;
}
相关文章:

202109-3 CCF 脉冲神经网络 66分题解 + 解题思路 + 解题过程
解题思路 根据题意,脉冲源的阈值大于随机数时,会向其所有出点发送脉冲 神经元当v>30时,会向其所有出点发送脉冲,unordered_map <int, vector > ne; //存储神经元/脉冲源的所有出点集合vector 所有脉冲会有一定的延迟&am…...

Aurora简介
Amazon Aurora是一种兼容MySQL和PostgreSQL的商用级别关系数据库,它既有商用数据库的性能和可用性(比如Oracle数据库),又具有开源数据库的成本效益(比如MySQL数据库)。 Aurora的速度可以达到MySQL数据库的…...

【python实操】用python写软件弹窗
文章目录前言组件label 与 多行文本复选框组件Radiobutton单选组件Frame框架组件labelframe标签框架列表框Listboxscrollbar滚动条组件scale刻度条组件spinbox组件Toplevel子窗体组件PanedWindow组件Menu下拉菜单弹出菜单总结针对组件前言 python学习之路任重而道远࿰…...

Ubuntu 常用操作
版本22.04 1、开启 root # 输入新密码 sudo passwd rootUbuntu以root账号登录桌面 默认情况是不允许用root帐号直接登录图形界面的。 Ubuntu 默认使用 GNOME,GNOME 使用 GDM 显示管理器。 为了允许以 root 身份登录到 GNOME,你需要对位于 /etc/…...

井字棋--课后程序(Python程序开发案例教程-黑马程序员编著-第7章-课后作业)
实例2:井字棋 井字棋是一种在3 * 3格子上进行的连珠游戏,又称井字游戏。井字棋的游戏有两名玩家,其中一个玩家画圈,另一个玩家画叉,轮流在3 * 3格子上画上自己的符号,最先在横向、纵向、或斜线方向连成一条…...
谷粒学院开发(三):统一日志、异常及前端准备工作
特定异常处理 ControllerAdvice public class GlobalExceptionHandler {ExceptionHandler(Exception.class) // 指定出现什么异常会被处理ResponseBody // 为了能够返回数据public R error(Exception e) {e.printStackTrace();return R.error().message("执行了全局异常…...
| 机考必刷)
华为OD机试题 - 招聘(JavaScript)| 机考必刷
更多题库,搜索引擎搜 梦想橡皮擦华为OD 👑👑👑 更多华为OD题库,搜 梦想橡皮擦 华为OD 👑👑👑 更多华为机考题库,搜 梦想橡皮擦华为OD 👑👑👑 华为OD机试题 最近更新的博客使用说明本篇题解:招聘题目输入输出示例一输入输出说明示例二输入输出说明示例三输…...

关于SQL优化的几点说明
1. ORACLE DBA是如何进行SQL优化的 作为一个Oracle数据库管理员(DBA),SQL优化是他们的日常工作之一,主要目标是优化查询性能,减少查询时间,并提高数据库的整体性能。 以下是Oracle DBA如何进行SQL优化的一般流程: 监控…...
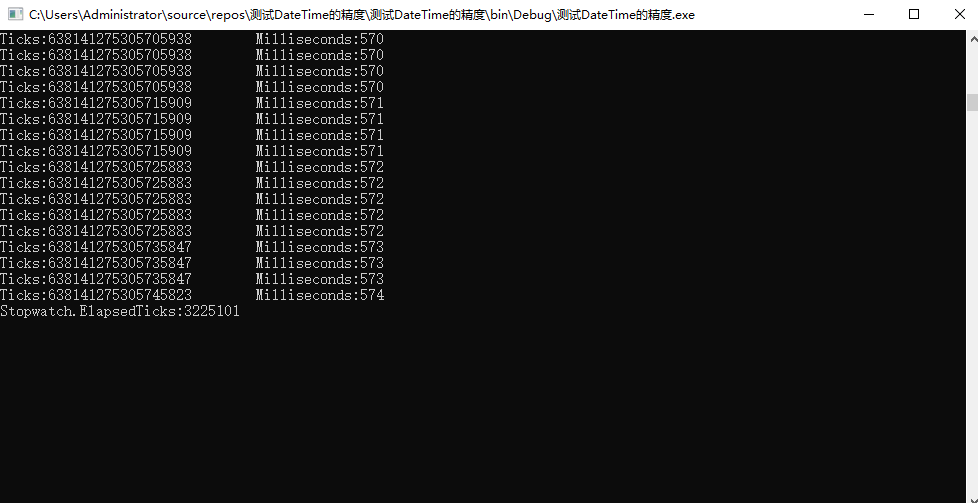
使用高精度秒表StopWatch测试DateTime.Now的精度
StopWatch使用的命名空间:using System.Diagnostics;StopWatch的使用方法:创建Stopwatch对象:stopwatch;stopwatch计时表开启:stopwatch.Start();stopwatch计时表关闭:stopwatch.Stop();计算stopwatch.Stop…...
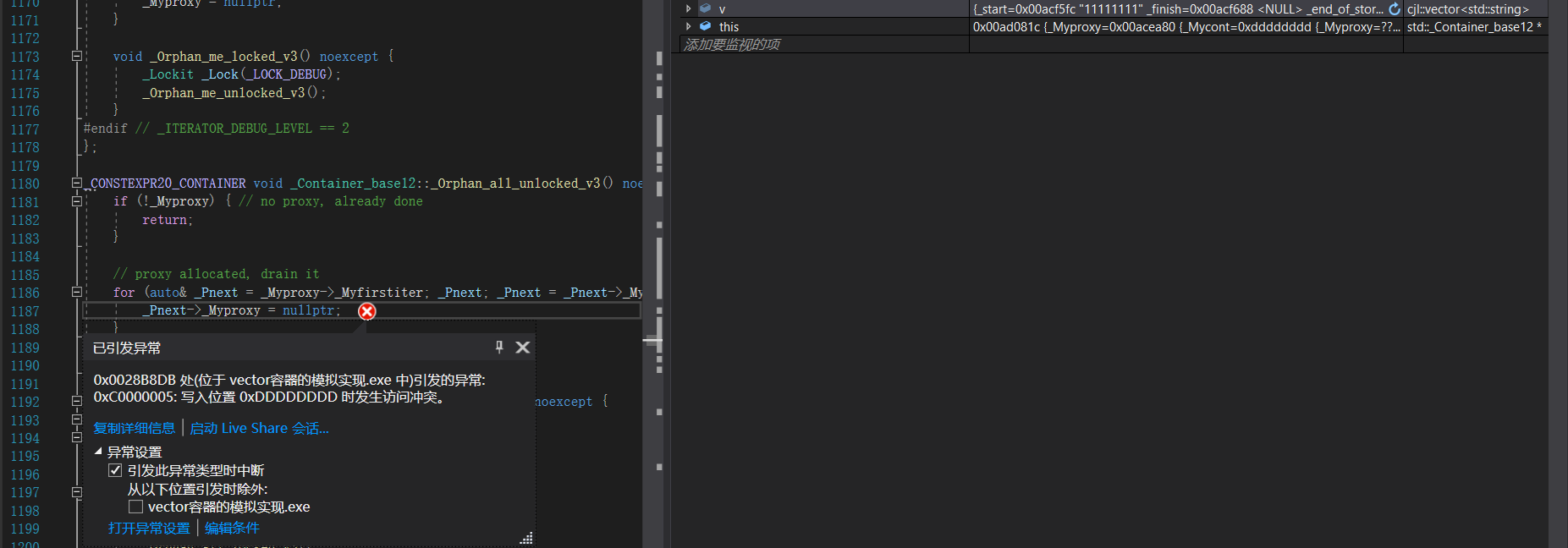
【C++】vector的使用及其模拟实现
这里写目录标题一、vector的介绍及使用1. vector的介绍2. 构造函数3. 遍历方式4. 容量操作及空间增长问题5. 增删查改6. vector二维数组二、vector的模拟实现1. 构造函数2. 迭代器和基本接口3. reserve和resize4. push_back和pop_back5. insert和erase5. 迭代器失效问题5. 浅拷…...
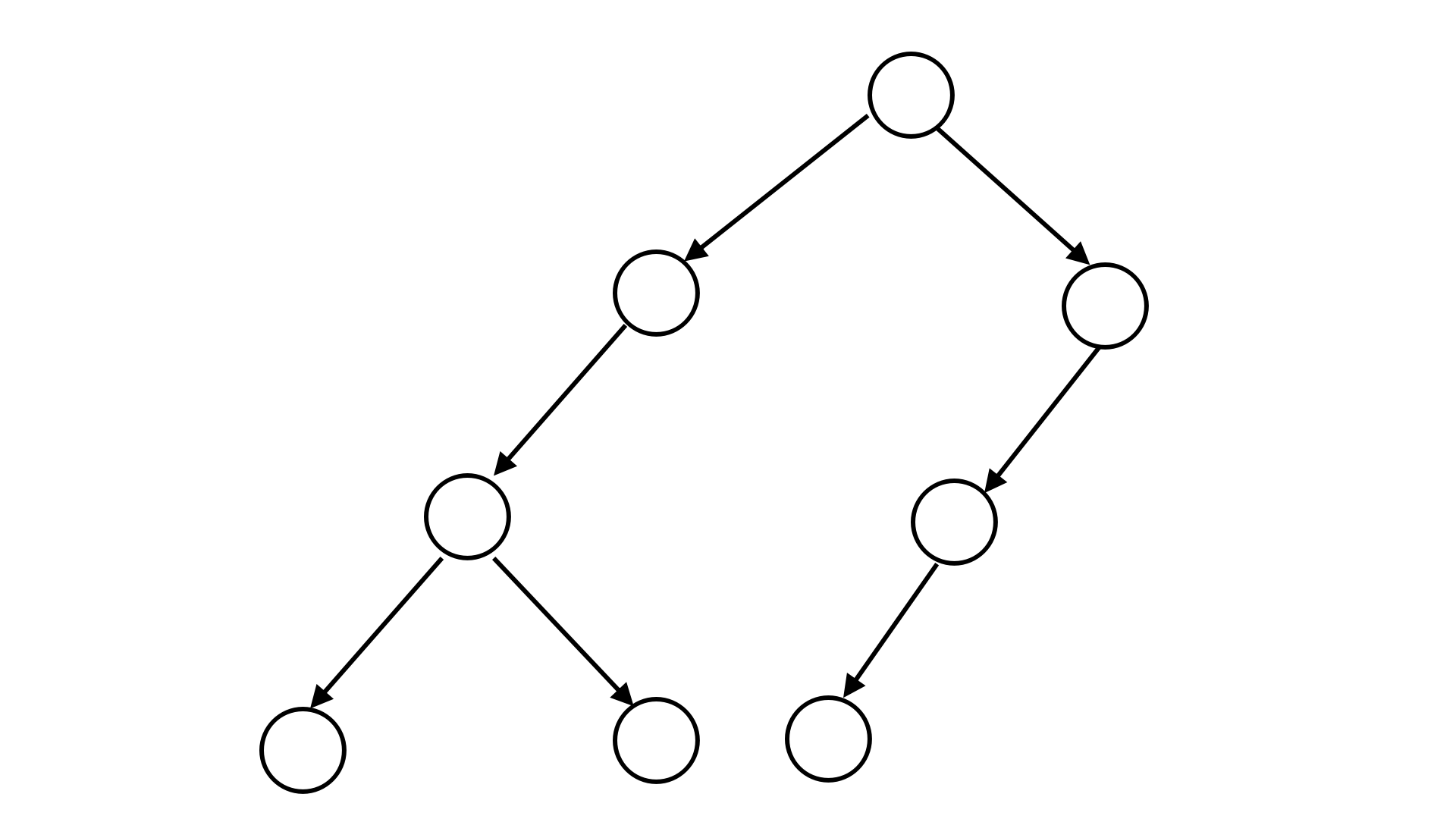
[洛谷-P2585][ZJOI2006]三色二叉树(树形DP+状态机DP)
[洛谷-P2585][ZJOI2006]三色二叉树(树形DP状态机DP)一、题目题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示数据规模与约定二、分析1、递归建树2、树形DP 状态机DP(1)状态表示(2)状态转移三、…...

BI技巧丨计算组
PowerBI有三大工具,分别是DAX Studio,Tabular Editor和Bravo。 DAX Studio通常我们会用来进行性能分析和DAX调优使用,Bravo一般用来批量格式化DAX,而Tabular Editor主要的功能就是计算组。 计算组这个名词,相信很多小伙…...
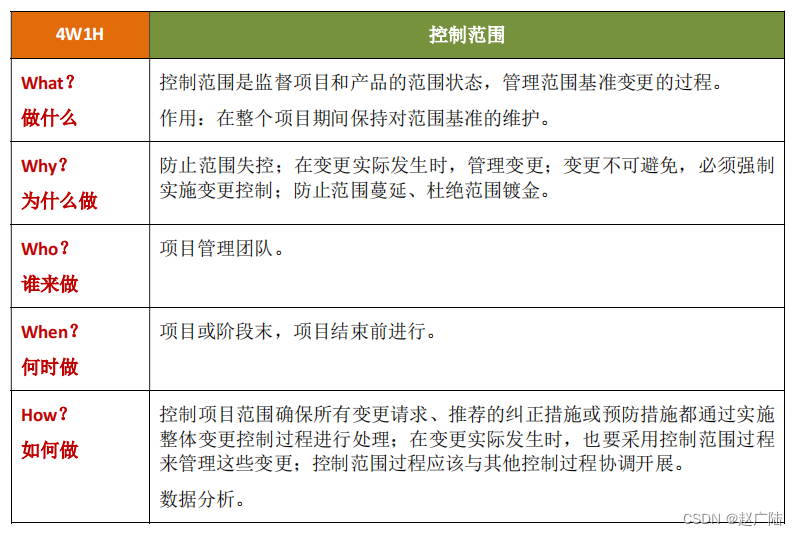
PMP项目管理项目范围管理
目录1 项目范围管理概述2 规划范围管理3 收集需求4 定义范围5 创建 WBS6 确认范围7 控制范围1 项目范围管理概述 项目范围管理包括确保项目做且只做所需的全部工作,以成功完成项目的各 个过程。管理项目范围主要在于定义和控制哪些工作应在项目内,哪些工…...

Flink 定时加载数据源
一、简介 flink 自定义实时数据源使用流处理比较简单,比如 Kafka、MQ 等,如果使用 MySQL、redis 批处理也比较简单 如果需要定时加载数据作为 flink 数据源使用流处理,比如定时从 mysql 或者 redis 获取一批数据,传入 flink 做处…...

ChatGPT、人工智能、人类和一些酒桌闲聊
© 2023 Conmajia Initiated 10th March, 2023 昨天跟某化学家喝酒,期间提到了 ChatGPT。他的评价是:这鬼东西大量输出毫无意义、错漏百出甚至是虚假的信息,“in a confident accent”。例如某次 GPT 针对“描述某某记者”这一问题&#…...

WebRTC开源库内部调用abort函数引发程序发生闪退问题的排查
目录 1、初始问题描述 2、使用Process Explorer工具查看到处理音视频业务的rtcmpdll.dll模块没有加载起来 3、使用Dependency Walker工具查看到rtcmpdll.dll依赖的库有问题 4、更新库之后Debug程序启动时就发生异常,程序闪退 5、VS调试时看不到有效的函数调用堆…...

Golang并发编程
Golang并发编程 文章目录Golang并发编程1. 协程2. channel2.1 channel的创建2.2 使用waitGroup实现同步3. 并发编程3.1 并发编程之runtime包3.2 mutex互斥锁3.3 channel遍历3.3.1 for if遍历3.3.2 for range3.4 select switch3.5 Timer3.5.1 time.NewTimer()3.5.2 Stop、reset…...
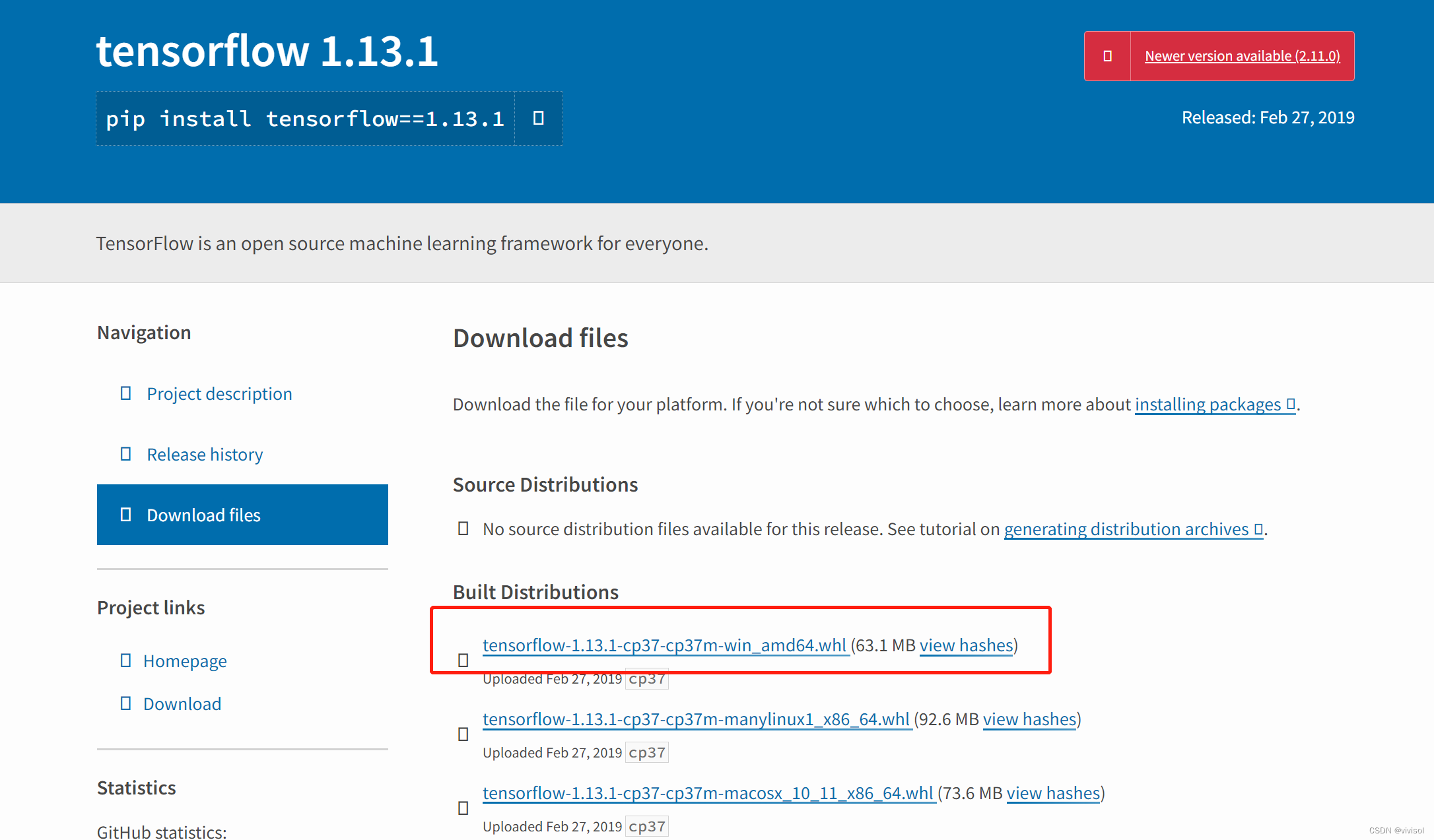
windows+Anaconda环境下安装BERT成功安装方法及问题汇总
前言 在WindowsAnaconda环境下安装BERT,遇到各种问题,几经磨难,最终成功。接下来,先介绍成功的安装方法,再附上遇到的问题汇总 成功的安装方法 1、创建虚拟环境 注意:必须加上python3.7.12以创建环境&a…...
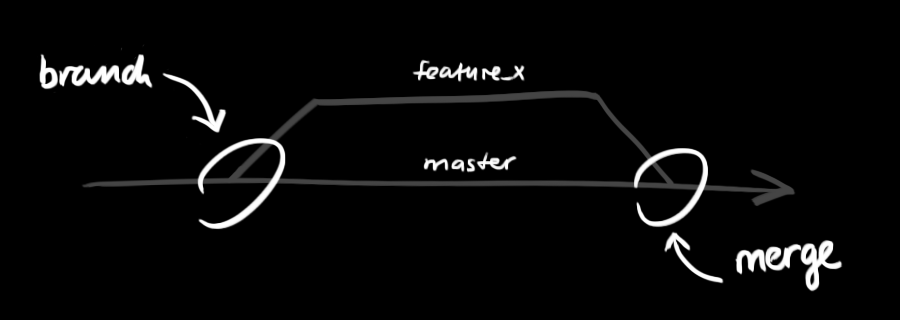
git - 简易指南
git - 简易指南 创建新仓库 创建新文件夹,打开,然后执行 git init 以创建新的 git 仓库。 检出仓库 执行如下命令以创建一个本地仓库的克隆版本: git clone /path/to/repository 如果是远端服务器上的仓库,你的命令会是这个样…...

[论文笔记]Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context
引言 我们知道Transformer很好用,但它设定的最长长度是512。像一篇文章超过512个token是很容易的,那么我们在处理这种长文本的情况下也想利用Transformer的强大表达能力需要怎么做呢? 本文就带来一种处理长文本的Transformer变种——Transf…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

鸿蒙Navigation路由导航-基本使用介绍
1. Navigation介绍 Navigation组件是路由导航的根视图容器,一般作为Page页面的根容器使用,其内部默认包含了标题栏、内容区和工具栏,其中内容区默认首页显示导航内容(Navigation的子组件)或非首页显示(Nav…...

【汇编逆向系列】六、函数调用包含多个参数之多个整型-参数压栈顺序,rcx,rdx,r8,r9寄存器
从本章节开始,进入到函数有多个参数的情况,前面几个章节中介绍了整型和浮点型使用了不同的寄存器在进行函数传参,ECX是整型的第一个参数的寄存器,那么多个参数的情况下函数如何传参,下面展开介绍参数为整型时候的几种情…...
