黑神话悟空-吉吉国王版本【抢先版】

在中国的游戏市场中,一款名为“黑神话悟空”的游戏引起了广泛的关注。这款游戏以中国传统的神话故事“西游记”为背景,创造了一个令人震撼的虚拟世界。今天,我们要来介绍的是这款游戏的一种特殊版本,那就是吉吉国王版本。
在吉吉国王版本中,主角悟空将面临全新的挑战和冒险。他将进入神秘的吉吉国,与那里的国王进行一场生死对决。这个版本的故事设置和角色设定都非常独特,为玩家提供了全新的游戏体验。
在吉吉国王版本中,悟空的形象和能力也有所改变。他不再是我们熟悉的那个戏谑的猴子,而是变成了一个充满威严和力量的国王。他的能力也更加强大,能够使用各种神奇的武器和技能。
同时,吉吉国王版本的故事线也非常吸引人。在这个版本中,悟空将面临来自吉吉国王的各种挑战和试炼。他需要通过智谋和勇气,才能够打败吉吉国王,解救被他囚禁的百姓。
此外,吉吉国王版本的画面和音效也非常出色。游戏的画面细腻且富有想象力,将吉吉国的神秘和奇幻完美地展现出来。而游戏的音效则栩栩如生,为玩家提供了极致的视听享受。
总的来说,黑神话悟空的吉吉国王版本是一款非常值得尝试的游戏。无论你是喜欢中国神话,还是喜欢角色扮演游戏,都可以在这款游戏中找到乐趣。所以,如果你还没有尝试过这款游戏,那么现在就是最好的时机。让我们一起踏上这场奇幻的冒险之旅吧!

相关文章:

黑神话悟空-吉吉国王版本【抢先版】
在中国的游戏市场中,一款名为“黑神话悟空”的游戏引起了广泛的关注。这款游戏以中国传统的神话故事“西游记”为背景,创造了一个令人震撼的虚拟世界。今天,我们要来介绍的是这款游戏的一种特殊版本,那就是吉吉国王版本。 在吉吉国…...
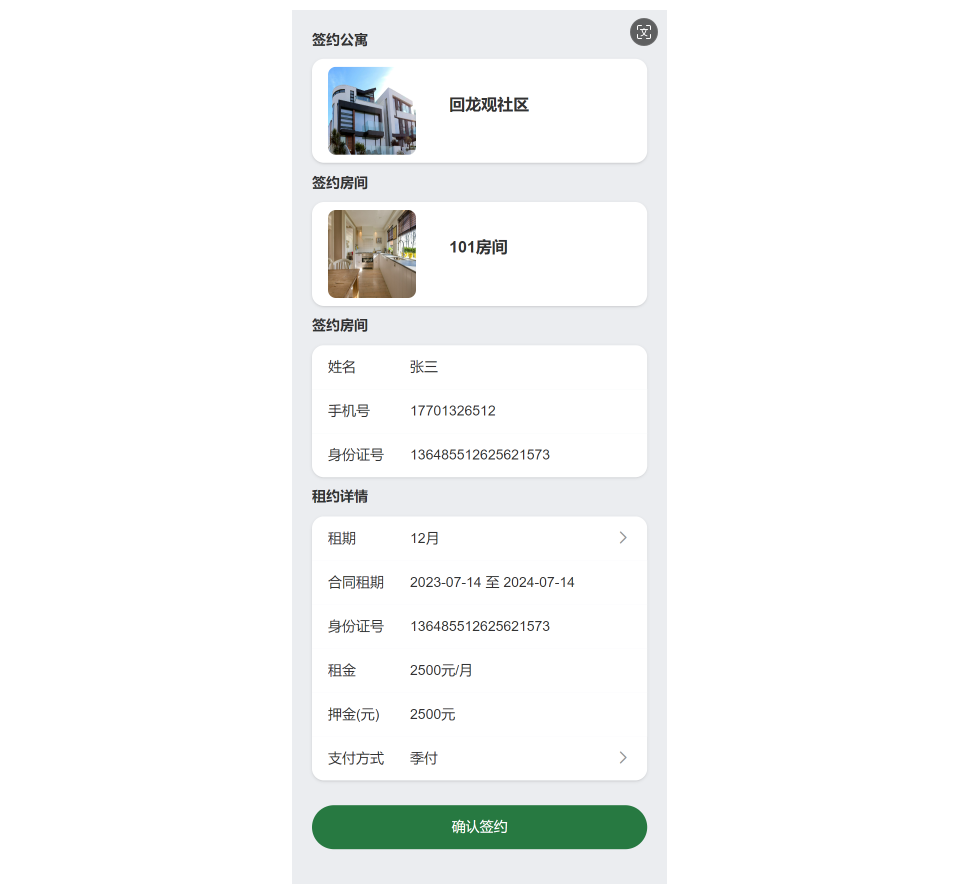
【尚庭公寓SpringBoot + Vue 项目实战】预约看房与租约管理(完结)
【尚庭公寓SpringBoot Vue 项目实战】预约看房与租约管理(完结) 文章目录 【尚庭公寓SpringBoot Vue 项目实战】预约看房与租约管理(完结)1、业务说明2、接口开发2.1、预约看房管理2.1.1.保存或更新看房预约2.1.2. 查询个人预约…...

java拼图小游戏项目
创建一个Java拼图小游戏是一个有趣且富有教育意义的项目,可以锻炼你的编程技能。以下是开发一个基本拼图游戏可能需要考虑的几个步骤: 项目规划: 确定游戏的基本规则和玩法。设计游戏的界面和用户交互。 环境搭建: 确保你的开发环…...
[C++][数据结构][跳表]详细讲解
目录 0.什么是跳表?1.SkipList的优化思路2.SkipList的效率如何保证?3.SkipList实现4.SkipList VS 平衡搜索树 && Hash 0.什么是跳表? SkipList本质上也是一种查找结构,用于解决算法中的查找问题,跟平衡搜索树…...

tinyxml
github下载相关的软件包,其中有四个文件需要主要需要关注就是分别是tinyxml12.cpp,tinyxml12.h,rss网页xml文件,还有就是官方给的test文件tinyxmltest.cpp。 example1就是提供一个打开文件的方式 int example_1() {XMLDocument …...
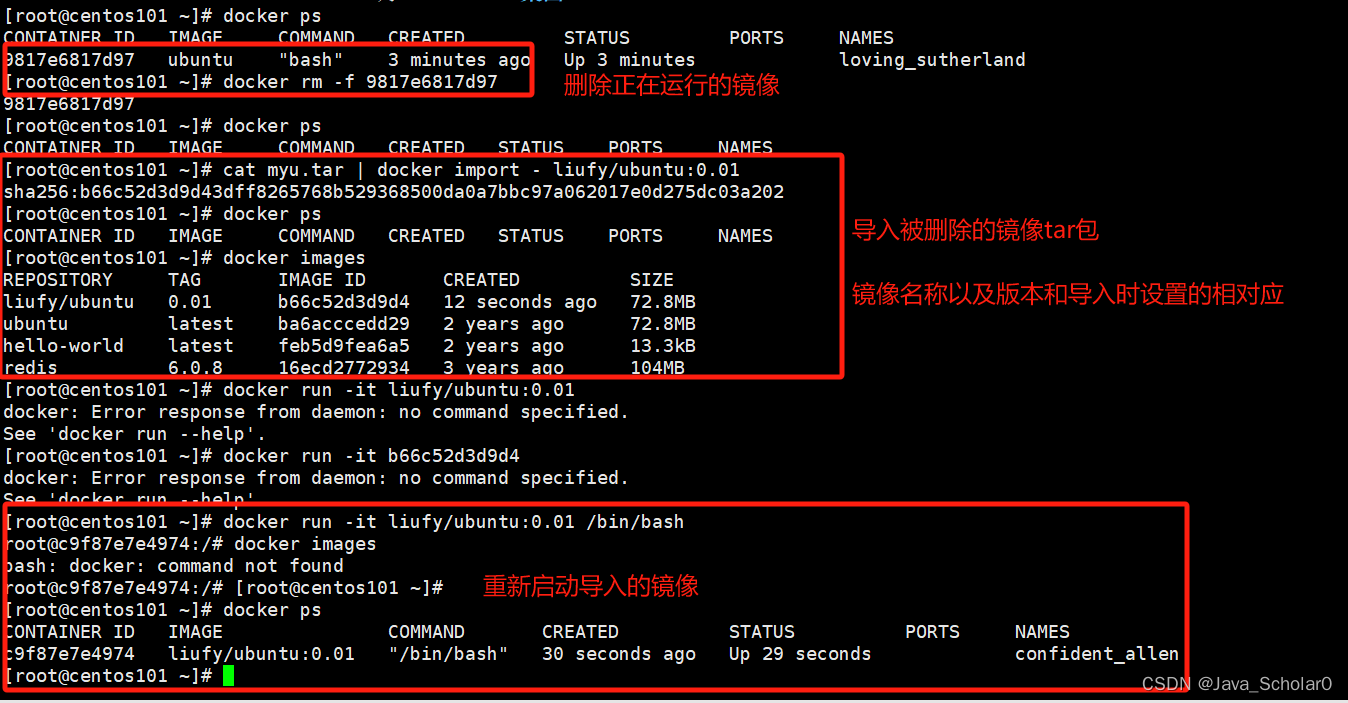
Docker(三)-Docker常用命令
1.run run命令执行流程:2.帮助启动类命令 2.1 启动docker systemctl start docker2.2 停止docker systemctl stop docker2.3 重启docker systemctl restart docker2.4查看docker状态 systemctl status docker2.5开机启动 systemctl enable docker2.6查看docker概要信息 …...
[MRCTF2020]PixelShooter
一个apk文件 jeb打开发现是apk文件 apk游戏逆向必须知道的知识: 一般关键数据在 Assets/bin/data/managed/assembly-csharp.dll这个文件里面 我不知道jeb为什么这里我没有 apk是个压缩包 直接解压 这个文件解压也可以发现flag {Unity_1S_Fun_233}...

vue实现的商品列表网页
一、商品列表效果如下 二、代码; vue实现的商品列表网页 , 图片在vue项目的Public文件夹里的 imgs中 <template><div class"common-layout"><!-- el-container:外层容器。 当子元素中包含 <el-header> 或 <el-foo…...

【泛微系统】e-cology非标配功能概览
关于泛微非标功能的功能编号、功能名称及支持版本 编号名称支持版本001考勤功能4.500.0124-9.00+KB900190206002短信通用接口5.000.0327+KB50001003 及以上版本004计划任务接口5.0+KB50001003及以上版本005集成登录接口6.0及以上版本006流程中自定义浏览框5.0+KB50001003及以上…...

Python基础教程(二十八):pip模块
💝💝💝首先,欢迎各位来到我的博客,很高兴能够在这里和您见面!希望您在这里不仅可以有所收获,同时也能感受到一份轻松欢乐的氛围,祝你生活愉快! 💝Ὁ…...

通信系统概述
1.定义 通信系统(也称为通信网络)是利用各种通信线路将地理上分散的、具有独立功能的计算机系统和通信设备按不同的形式连接起来,依靠网络软件及通信协议实现资源共享和信息传递的系统。 2.概述 随着通信技术和网络技术的不断发展ÿ…...
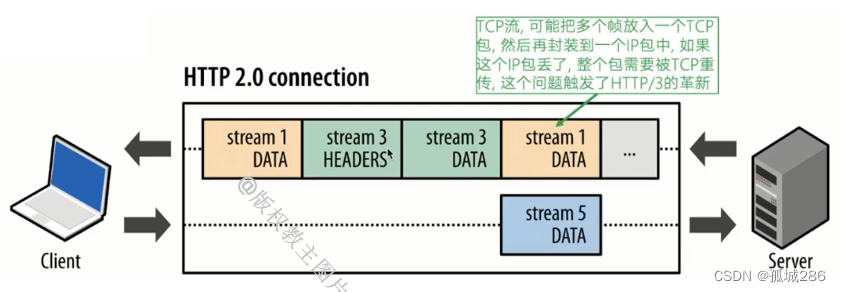
http发展史(http0.9、http1.0、http1.1、http/2、http/3)详解
文章目录 HTTP/0.9HTTP/1.0HTTP/1.1队头阻塞(Head-of-Line Blocking)1. TCP 层的队头阻塞2. HTTP/1.1 的队头阻塞 HTTP/2HTTP/3 HTTP/0.9 发布时间:1991年 特点: 只支持 GET 方法没有 HTTP 头部响应中只有 HTML 内容࿰…...
)
Hadoop 面试题(四)
1. 简述Hadoop节点的动态上线下线的大概操作 ? 在Hadoop集群中,节点的动态上下线指的是在不停止整个集群服务的情况下,添加或移除节点。这种能力对于维护和扩展集群非常重要。以下是Hadoop节点动态上线下线的大概操作步骤: 动态…...

绽放光彩的小程序 UI 风格
绽放光彩的小程序 UI 风格...
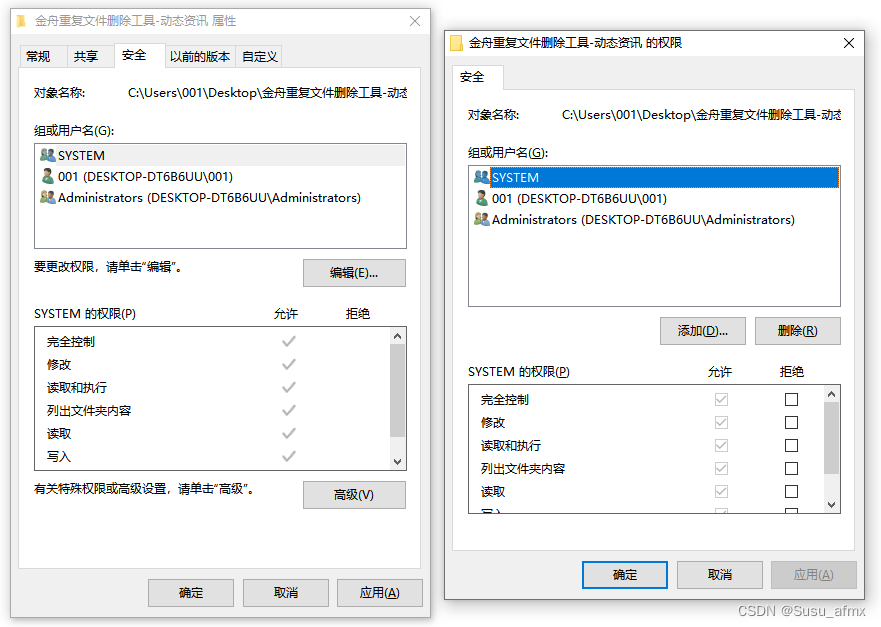
电脑文件夹怎么加密?文件夹加密的5种方法
在数字化时代,信息安全显得尤为重要。对于个人电脑用户来说,文件夹加密是一种有效保护隐私和数据安全的方法。本文将介绍五种文件夹加密的方法,帮助您更好地保护自己的重要文件。 如何设置文件夹密码方法一:利用Windows系统自带的…...

异步复位同步释放
目录 描述 输入描述: 输出描述: 参考代码 描述 题目描述: 请使用异步复位同步释放来将输入数据a存储到寄存器中,并画图说明异步复位同步释放的机制原理 信号示意图: clk为时钟 rst_n为低电平复位 d信号输入…...

JupyterLab使用指南(七):JupyterLab使用 LaTeX 生成数学公式
在 JupyterLab 中,可以使用 LaTeX 语法生成复杂的数学公式。JupyterLab 内置对 LaTeX 的支持,使得我们可以方便地在 notebook 中编写和展示数学公式。以下是详细的步骤和示例。 1. 使用 LaTeX 生成数学公式 LaTeX 是一种专门用于排版数学公式的语言。J…...
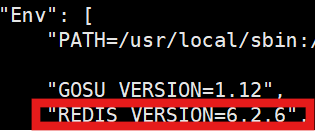
docker 环境部署
1.Redis部署 用docker拉取redis镜像 docker pull redis 用docker查看拉取的镜像版本号,这里查到的是 6.2.6 版本 docker inspect redis 通过wget指令下载对应版本的tar包,下载完成后解压 wget https://download.redis.io/releases/redis-6.2.6.tar.gz …...

Spring中的ContextPath总结
Spring中的ContextPath总结 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 1. ContextPath的概念 在Spring中,ContextPath是指Web应用程序的上下文…...

C++设计模式——Composite组合模式
一,组合模式简介 真实世界中,像企业组织、文档、图形软件界面等案例,它们在结构上都是分层次的。将系统分层次的方式使得统一管理和添加不同子模块变得容易,在软件开发中,组合模式的设计思想和它们类似。 组合模式是…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...
