模拟退火算法
模拟退火算法(Simulated Annealing, SA)是一种用于全局优化问题的概率搜索算法,其灵感来自于金属退火过程。在金属退火中,材料被加热到高温,然后缓慢冷却,以减少其晶格中的缺陷并达到最小能量状态。模拟退火算法通过模拟这一过程来寻找全局最优解,避免陷入局部最优解。
算法原理
模拟退火算法的基本思想是通过引入随机扰动和逐步降低温度,逐渐收敛到全局最优解。算法的主要步骤如下:
1. **初始化**:
- 设定初始温度 \( T_0 \)。
- 选择一个初始解 \( x_0 \)。
2. **迭代过程**:
- 在当前温度 \( T \) 下,生成一个新的解 \( x_{\text{new}} \)。
- 计算新解和当前解的目标函数值之差 \( \Delta E = E(x_{\text{new}}) - E(x) \)。
- 如果 \( \Delta E < 0 \),接受新解(即新解优于当前解)。
- 如果 \( \Delta E \geq 0 \),以概率 \( P = \exp(-\Delta E / T) \) 接受新解(即有一定概率接受劣解,避免陷入局部最优)。
3. **温度更新**:
- 根据冷却计划逐步降低温度 \( T \)。
- 常用的冷却计划包括线性降温、指数降温和对数降温。
4. **终止条件**:
- 当温度降至一定值或达到最大迭代次数时,停止算法。
数学表示
模拟退火算法的数学表示如下:
1. **初始温度**: \( T_0 \)
2. **初始解**: \( x_0 \)
3. **目标函数**: \( E(x) \)
4. **新解生成**: \( x_{\text{new}} = \text{neighbor}(x) \)
5. **接受概率**:
\[
P(\Delta E) = \begin{cases}
1 & \text{if } \Delta E < 0 \\
\exp(-\Delta E / T) & \text{if } \Delta E \geq 0
\end{cases}
\]
6. **温度更新**: \( T_{k+1} = \alpha T_k \)
算法步骤
以下是模拟退火算法的具体步骤:
1. **初始化**:
```python
import random
import math
def initial_solution():
# 定义初始解生成方法
pass
def objective_function(x):
# 定义目标函数
pass
T = T0 # 初始温度
x = initial_solution() # 初始解
```
2. **迭代过程**:
```python
while T > Tmin and iter < max_iter:
x_new = generate_neighbor(x) # 生成新解
delta_E = objective_function(x_new) - objective_function(x) # 计算目标函数值之差
if delta_E < 0 or random.random() < math.exp(-delta_E / T):
x = x_new # 接受新解
T = alpha * T # 更新温度
iter += 1
```
3. **结果输出**:
```python
print("Optimal solution:", x)
print("Optimal value:", objective_function(x))
```
示例应用
以下是一个TSP(旅行商问题)示例,展示如何使用模拟退火算法求解:
1. **定义问题**:
- 给定一组城市及其之间的距离,寻找访问每个城市一次并返回起始城市的最短路径。
2. **实现模拟退火算法**:
```python
import random
import math
def distance(cities, tour):
# 计算旅行商路径的总距离
dist = 0
for i in range(len(tour)):
dist += cities[tour[i-1]][tour[i]]
return dist
def initial_solution(n):
# 生成初始解:一个随机的城市序列
tour = list(range(n))
random.shuffle(tour)
return tour
def generate_neighbor(tour):
# 生成新解:随机交换两个城市的位置
new_tour = tour[:]
i, j = random.sample(range(len(tour)), 2)
new_tour[i], new_tour[j] = new_tour[j], new_tour[i]
return new_tour
# 初始化参数
T0 = 100
Tmin = 1e-6
alpha = 0.99
max_iter = 1000
cities = [...] # 定义城市距离矩阵
n = len(cities)
T = T0
iter = 0
tour = initial_solution(n)
while T > Tmin and iter < max_iter:
new_tour = generate_neighbor(tour)
delta_E = distance(cities, new_tour) - distance(cities, tour)
if delta_E < 0 or random.random() < math.exp(-delta_E / T):
tour = new_tour
T *= alpha
iter += 1
print("Optimal tour:", tour)
print("Optimal distance:", distance(cities, tour))
```
优点与缺点
**优点**:
- **全局优化**:可以跳出局部最优,找到全局最优解。
- **简单灵活**:易于实现,适用于各种优化问题。
**缺点**:
- **参数调节**:性能依赖于初始温度、冷却计划等参数的选择。
- **收敛速度**:可能收敛较慢,尤其是在高维空间中。
参考文献
- **Kirkpatrick, S., Gelatt, C. D., and Vecchi, M. P. (1983)**. Optimization by Simulated Annealing. Science, 220(4598), 671-680.
- **Aarts, E., Korst, J., and Michiels, W. (2005)**. Simulated Annealing. In Search Methodologies (pp. 187-210). Springer, Boston, MA.
- **Eglese, R. W. (1990)**. Simulated Annealing: A Tool for Operational Research. European Journal of Operational Research, 46(3), 271-281.
通过对模拟退火算法的详细介绍及其在TSP中的应用,可以看出该算法在解决全局优化问题中的重要性。理解其原理和实现方法,有助于在各种实际问题中灵活应用。
相关文章:

模拟退火算法
模拟退火算法(Simulated Annealing, SA)是一种用于全局优化问题的概率搜索算法,其灵感来自于金属退火过程。在金属退火中,材料被加热到高温,然后缓慢冷却,以减少其晶格中的缺陷并达到最小能量状态。模拟退火…...

Java匿名类
Java 匿名类是一种特殊的内部类,它没有名字,并且通常用来简化代码实现,尤其是在实现接口或者抽象类的实例时。匿名类可以在实例化时定义其行为,而不需要创建单独的类文件。 匿名类的特点 没有名字:匿名类是没有名字的…...

G7易流赋能化工物流,实现安全、环保与效率的共赢
近日,中国物流与采购联合会在古都西安举办了备受瞩目的第七届化工物流安全环保发展论坛。以"坚守安全底线,追求绿色发展,智能规划化工物流未来"为主题,该论坛吸引了众多政府部门、行业专家和企业代表的参与。G7易流作为…...
)
y=sin(2x)
函数 \( y \sin(2x) \) 是一个正弦函数,其中 \( x \) 是自变量,\( y \) 是因变量。这个函数描述了一个周期性波动的波形,其特点是: 1. **振幅**:正弦函数的振幅是 1,这意味着波形在 \( y \) 轴上的最大值…...

快捷方式(lnk)--加载HTA-CS上线
免责声明:本文仅做技术交流与学习... 目录 CS: HTA文档 文件托管 借助mshta.exe突破 本地生成lnk快捷方式: 非系统图标路径不同问题: 关于lnk的上线问题: CS: HTA文档 配置监听器 有效载荷---->HTA文档--->选择监听器--->选择powershell模式----> 默认生成一…...

从同—视角理解扩散模型(Understanding Diffusion Models A Unified Perspective)
从同—视角理解扩散模型 Understanding Diffusion Models A Unified Perspective【全公式推导】【免费视频讲解】 B站视频讲解 视频的论文笔记 从同一视角理解扩散模型【视频讲解笔记】 配合视频讲解的同步笔记。 整个系列完整的论文笔记内容如下,仅为了不用—一回复…...
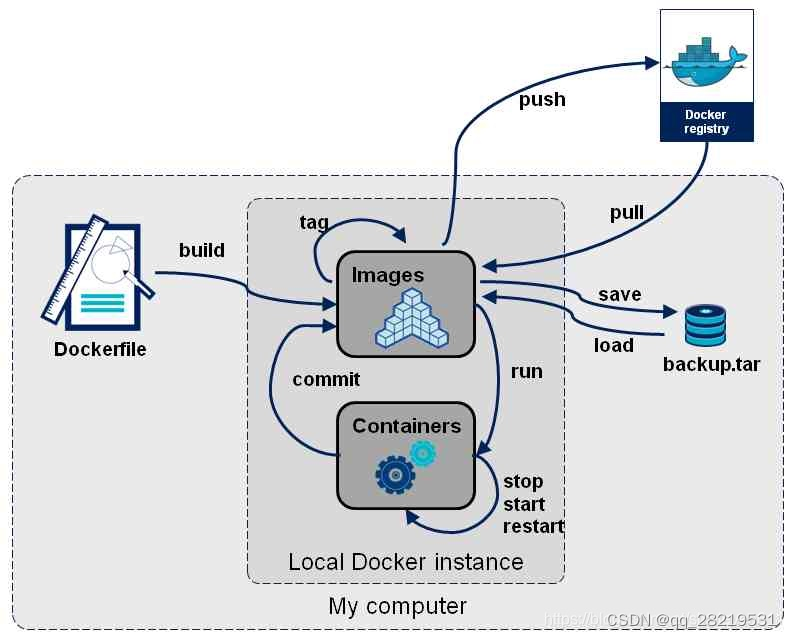
docker 基本用法及跨平台使用
一、Docker的优点 docker 主要解决的问题就是程序开发过程中编译和部署中遇到的环境配置的问题。 1.1 Docker与其他虚拟机层次结构的区别** 运行程序重点关注点在于环境。 VM虚拟机是基于Hypervisor虚拟化服务运行的。 Docker是基于内核的虚拟化技术实现的。 1.2 Docker的技…...
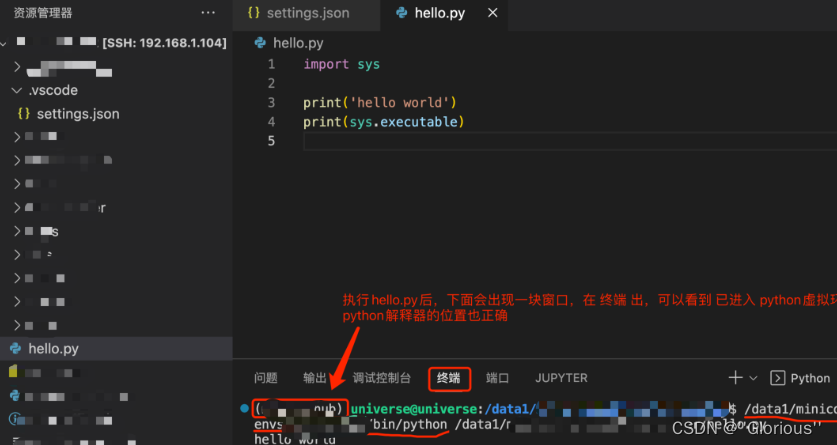
Vscode远程ubuntu
远程连接 到这里vscode远程到ubuntu和关闭远程连接,已完成 配置python环境 在远程目录下新建.vscode隐藏文件夹,文件夹里新建一个 settings.json 文件, 先远程服务器看下conda下的python虚拟环境位置 settings.json位置及内容如下 测试pyt…...
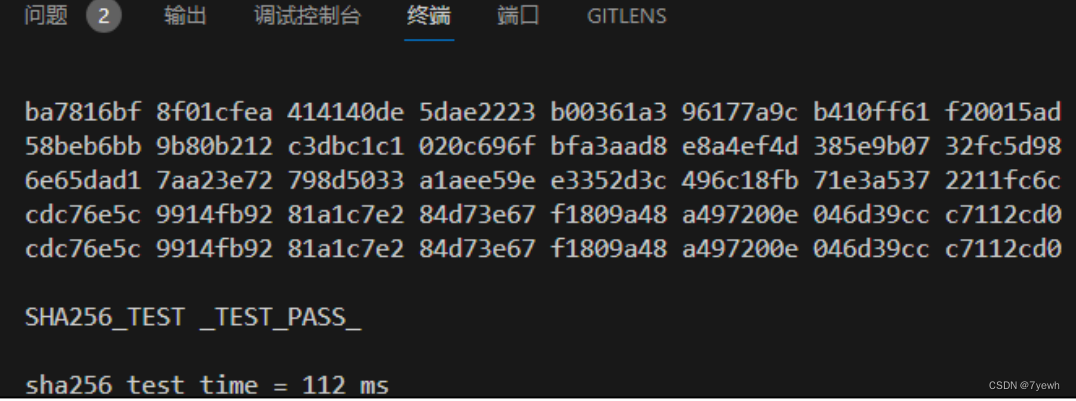
SHA256 安全散列算法加速器实验
1、SHA256 介绍 SHA256 加速器是用来计算 SHA-256 的计算单元, SHA256 是 SHA-2 下细分出的一种算法。 SHA-2 名称来自于安全散列算法 2 (英语: Secure Hash Algorithm 2 )的缩写,一种密码散列函 数算法标准…...

Elasticsearch-ES查询单字段去重
ES 语句 整体数据 GET wkl_test/_search {"query": {"match_all": {}} }结果: {"took" : 123,"timed_out" : false,"_shards" : {"total" : 1,"successful" : 1,"skipped" : 0…...

【Apache Doris】周FAQ集锦:第 7 期
【Apache Doris】周FAQ集锦:第 7 期 SQL问题数据操作问题运维常见问题其它问题关于社区 欢迎查阅本周的 Apache Doris 社区 FAQ 栏目! 在这个栏目中,每周将筛选社区反馈的热门问题和话题,重点回答并进行深入探讨。旨在为广大用户和…...

EE trade:炒伦敦金的注意事项及交易指南
在贵金属市场中,伦敦金因其高流动性和全球认可度,成为广大投资者的首选。然而,在炒伦敦金的过程中,投资者需要注意一些关键点。南华金业小编带您一起来看看。 国际黄金报价 一般国际黄金报价会提供三个价格: 买价(B…...
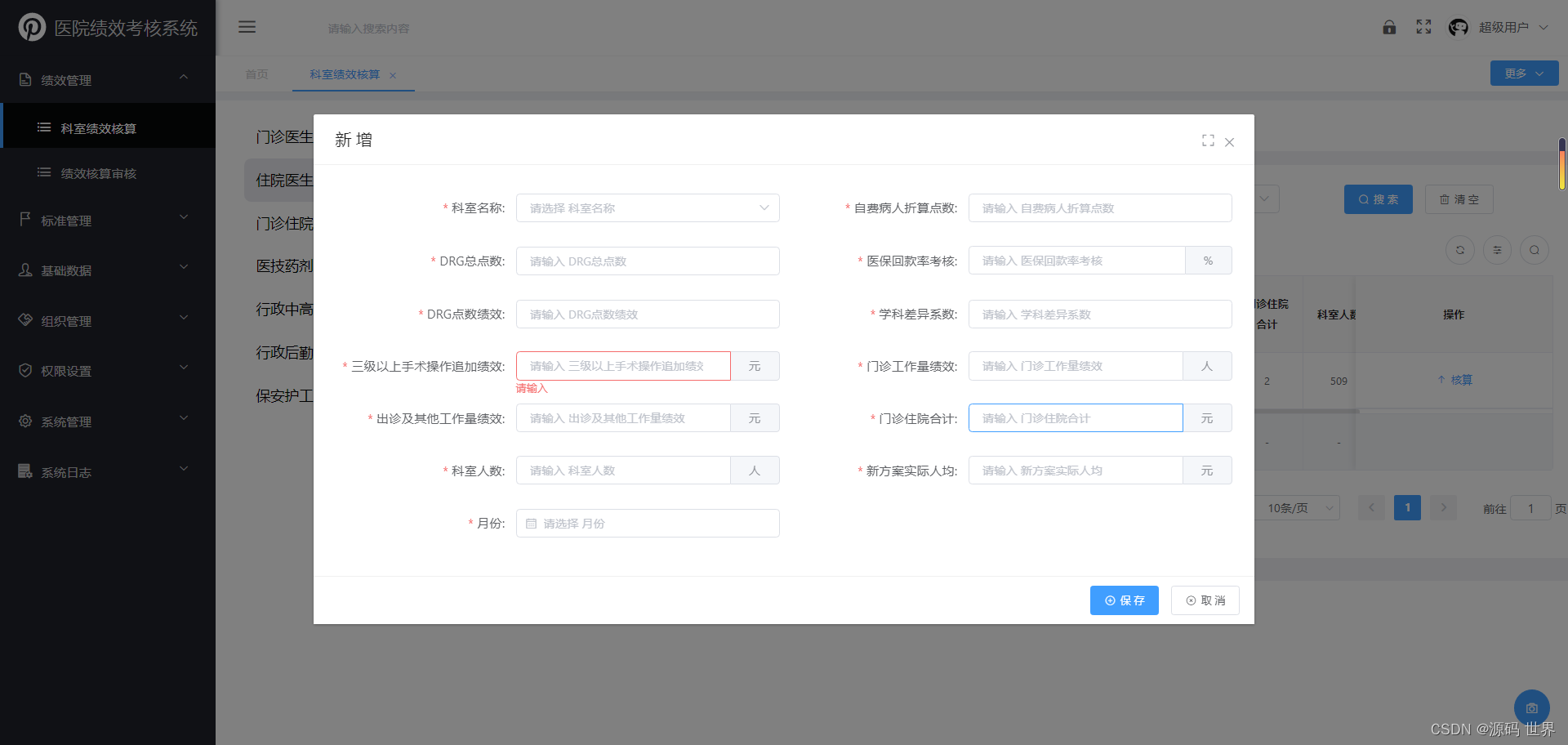
JAVA医院绩效考核系统源码 功能特点:大型医院绩效考核系统源码
JAVA医院绩效考核系统源码 功能特点:大型医院绩效考核系统源码 医院绩效管理系统主要用于对科室和岗位的工作量、工作质量、服务质量进行全面考核,并对科室绩效工资和岗位绩效工资进行核算的系统。医院绩效管理系统开发主要用到的管理工具有RBRVS、DRGS…...

Python神经影像数据的处理和分析库之nipy使用详解
概要 神经影像学(Neuroimaging)是神经科学中一个重要的分支,主要研究通过影像技术获取和分析大脑结构和功能的信息。nipy(Neuroimaging in Python)是一个强大的 Python 库,专门用于神经影像数据的处理和分析。nipy 提供了一系列工具和方法,帮助研究人员高效地处理神经影…...

非关系型数据库NoSQL数据层解决方案 之 Mongodb 简介 下载安装 springboot整合与读写操作
MongoDB 简介 MongoDB是一个开源的面向文档的NoSQL数据库,它采用了分布式文件存储的数据结构,是当前非常流行的数据库之一。 以下是MongoDB的主要特点和优势: 面向文档的存储: MongoDB是一个面向文档的数据库管理系统࿰…...

使用Redis优化Java应用的性能
使用Redis优化Java应用的性能 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们来探讨如何使用Redis优化Java应用的性能。Redis是一种开源的内存数据结构…...

基于Python的数据可视化大屏的设计与实现
基于Python的数据可视化大屏的设计与实现 Design and Implementation of Python-based Data Visualization Dashboard 完整下载链接:基于Python的数据可视化大屏的设计与实现 文章目录 基于Python的数据可视化大屏的设计与实现摘要第一章 导论1.1 研究背景1.2 研究目的1.3 研…...

什么是N卡和A卡?有什么区别?
名人说:莫听穿林打叶声,何妨吟啸且徐行。—— 苏轼《定风波莫听穿林打叶声》 本篇笔记整理:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 目录 一、什么是N卡和A卡?有什么区别?…...
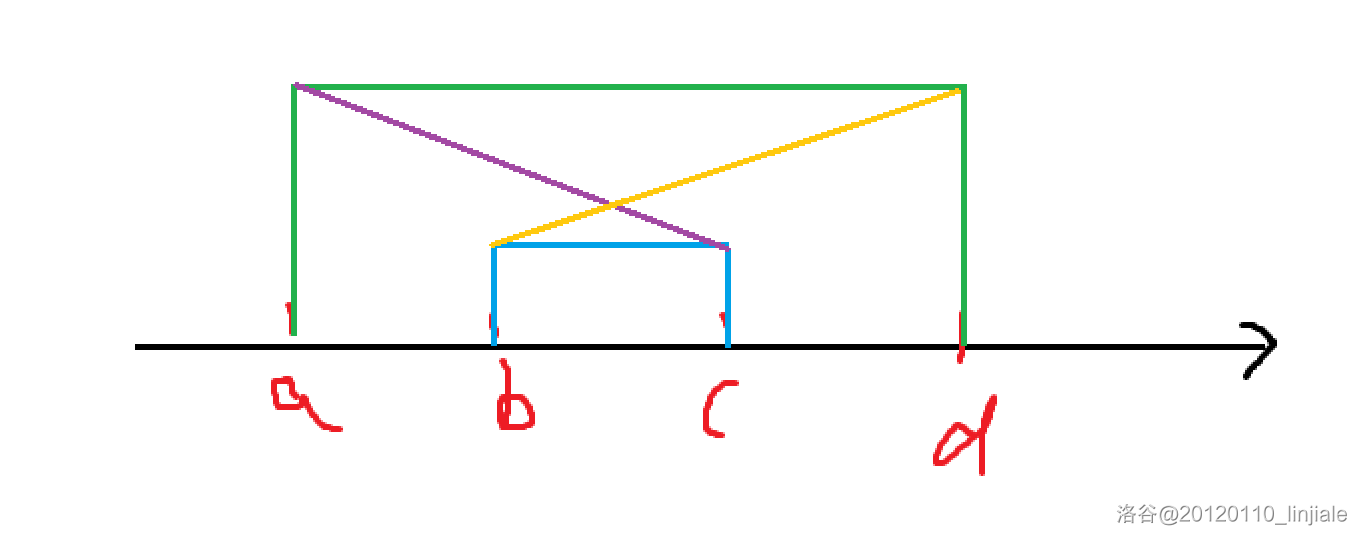
四边形不等式优化
四边形不等式优化 应用于类似以下dp转移方程。 f i min 1 ≤ j ≤ i ( w i , j , f i ) f_{i}\min_{1\le j\le i}(w_{i,j},f_{i}) fi1≤j≤imin(wi,j,fi) 假设 w i , j w_{i,j} wi,j 可以在 O ( 1 ) O(1) O(1) 的时间内进行计算。 在正常情况下,…...

这家民营银行起诉担保公司?暴露担保增信兜底隐患
来源 | 镭射财经(leishecaijing) 助贷领域中,各路资方依赖担保增信业务扩张数年,其风险积压也不容忽视。一旦助贷平台或担保公司兜不住底,资方就将陷入被动。 最近,一则民营银行起诉合作担保公司的消息引…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
