【Linux】基础IO_3
文章目录
- 六、基础I/O
- 3. 软硬链接
- 4. 动静态库
- 未完待续
六、基础I/O
3. 软硬链接
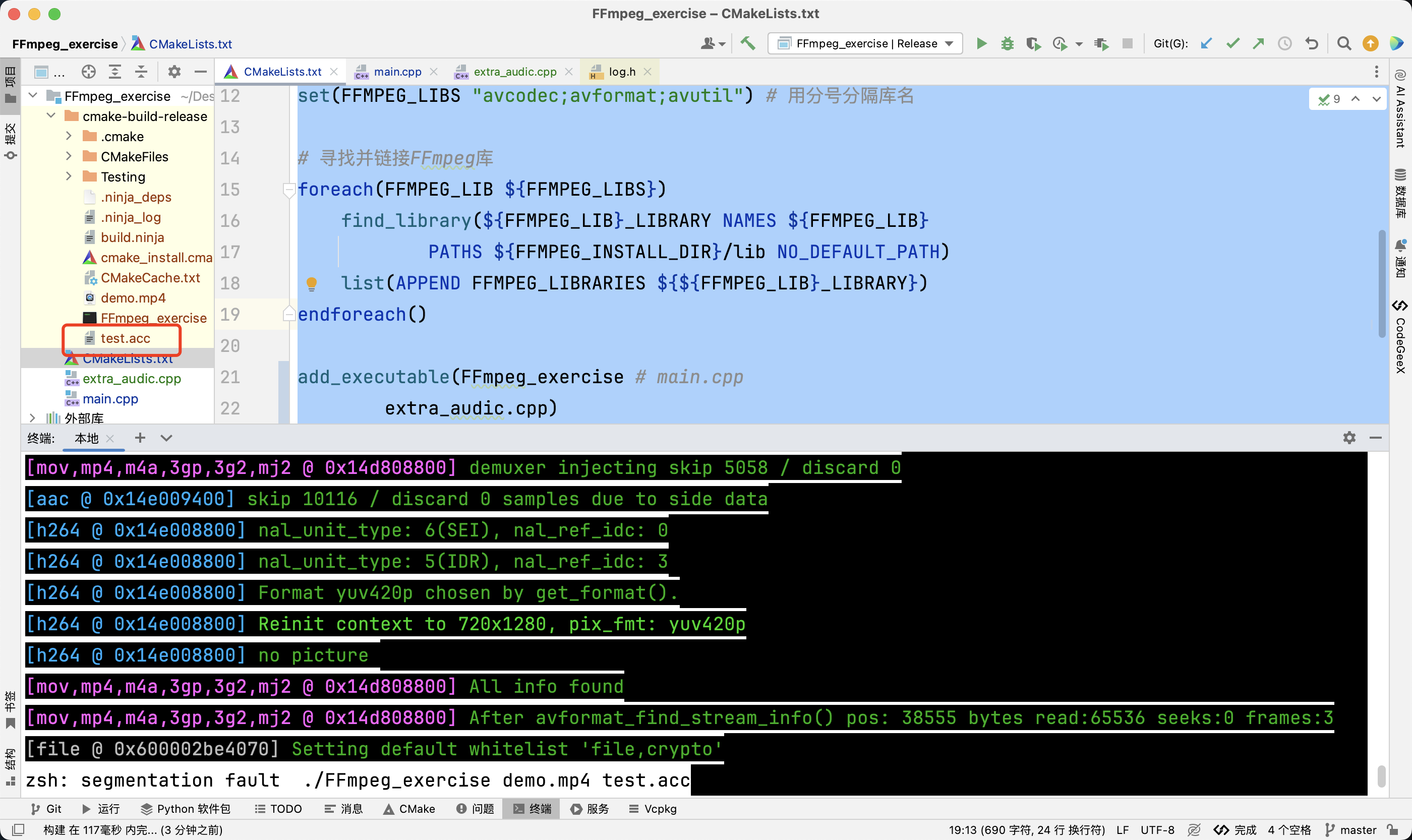
使用 ln 就可以创建链接,使用 ln -s 可以创建软链接,直接使用 ln 则是硬链接。
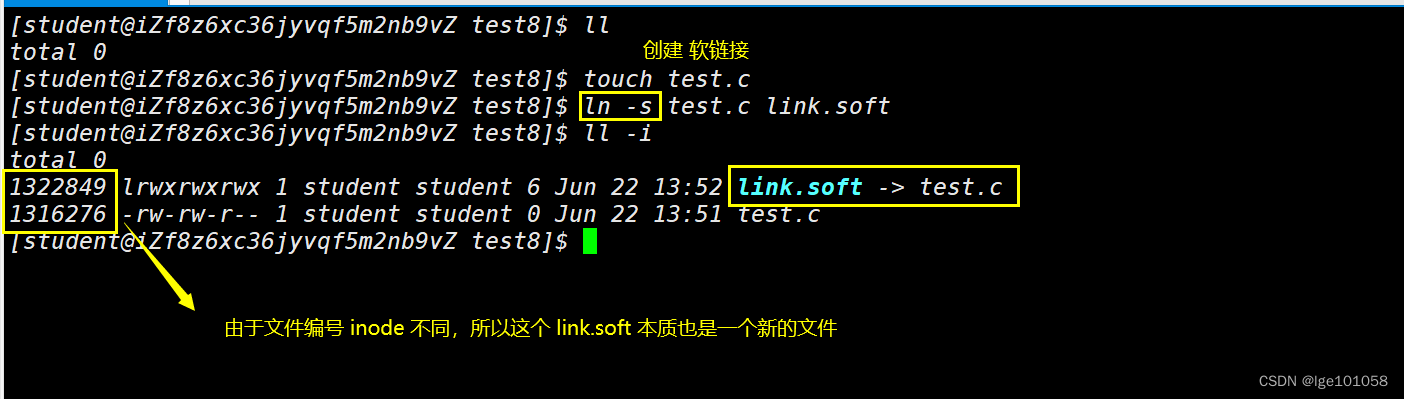
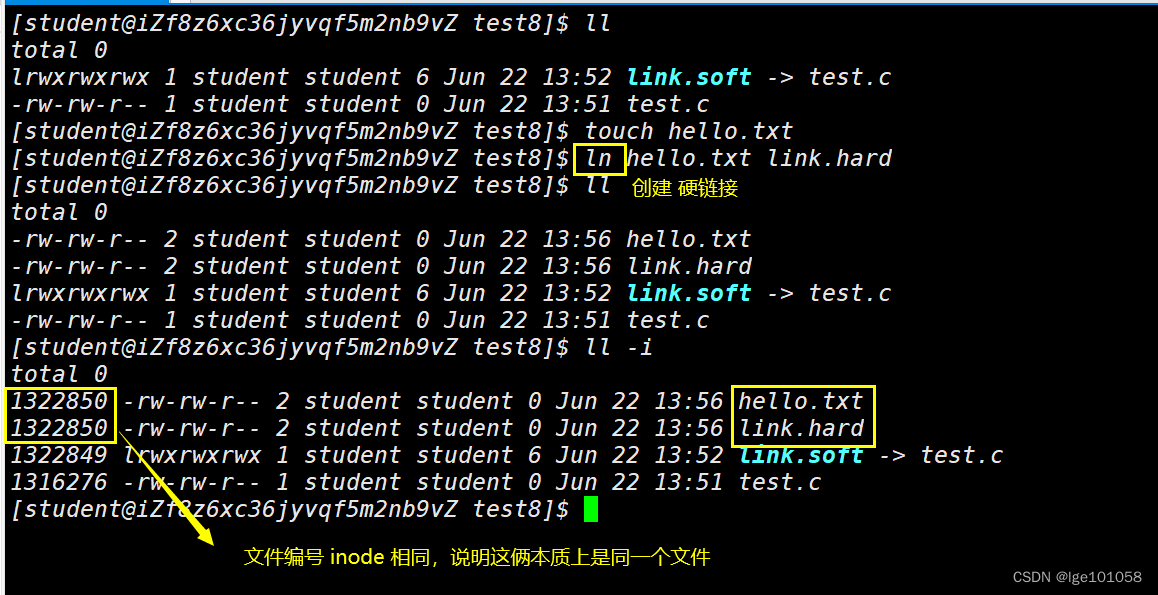
我们对硬链接进行测试一下:
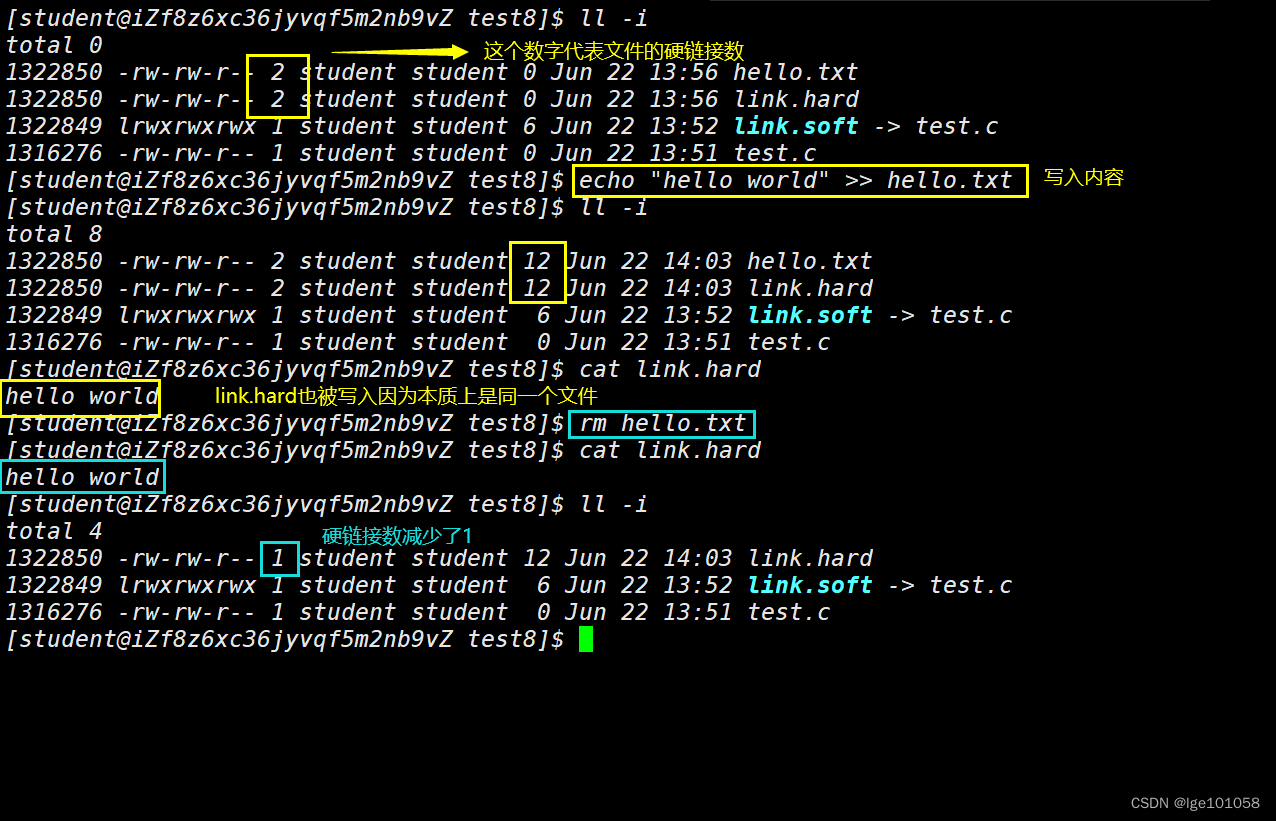
根据测试,我们知道了 硬链接就像一个重命名一样,向其中一个文件里面写,另一个也会改变 。但是删除后只会删除一个,这说明 文件的删除本质上是减少硬链接数。硬链接数从 1 变成 0 后才会清空文件的信息。
硬链接的本质就是在指定的目录下,插入新的文件名和目标文件的映射关系,并让inode的引用计数++。
软链接的本质就是一个独立文件,软链接内容里面放的是 目标文件的路径 。类似于 Windows 下的快捷方式。
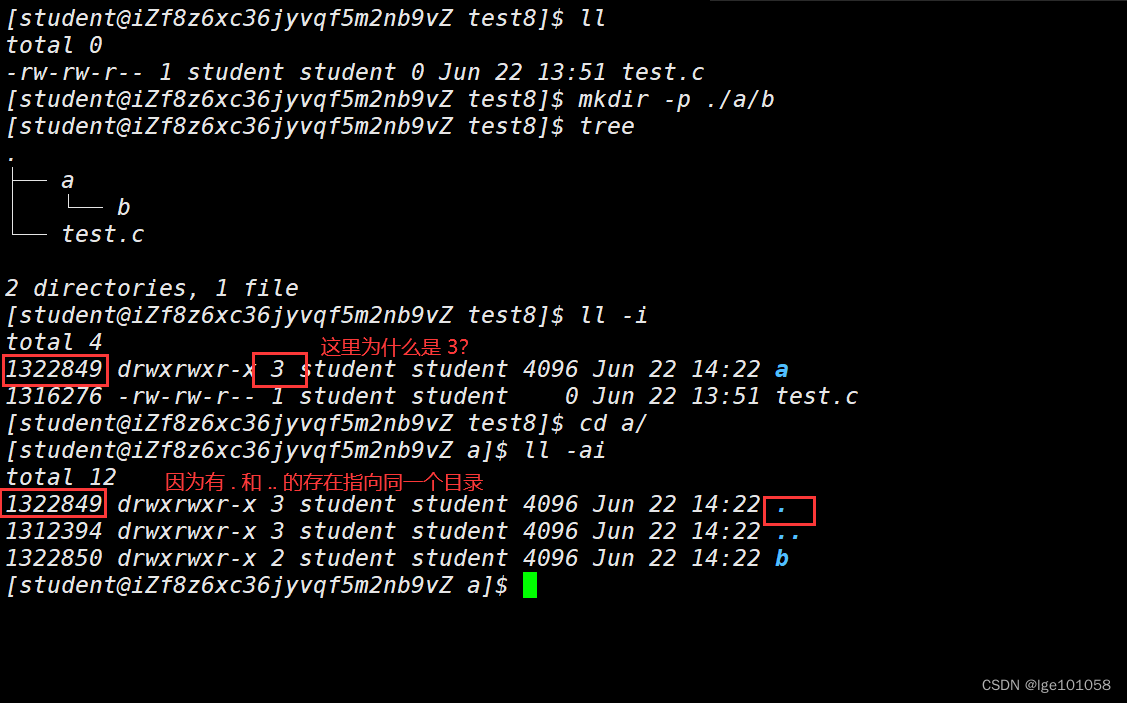
可以通过目录的硬链接数 -2 计算得到目录有多少个子目录。

可以给目录建立软链接,但是不能建立硬链接(除非系统建立的)。
4. 动静态库
我们之前使用过库,也对库有一定的了解,这里我们将对库进行更深入的理解。我们来自己创建一个库:
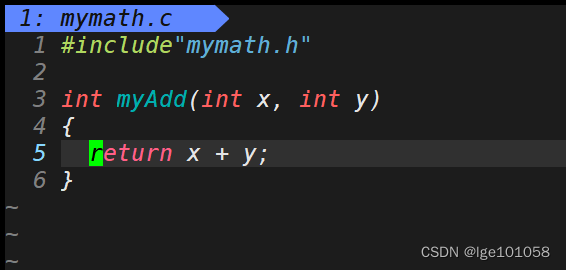
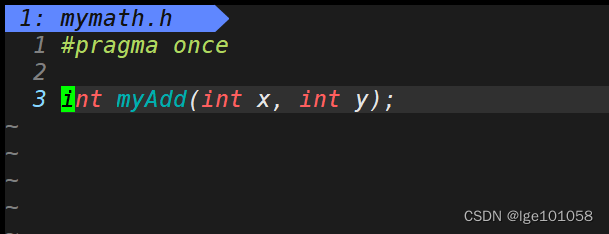
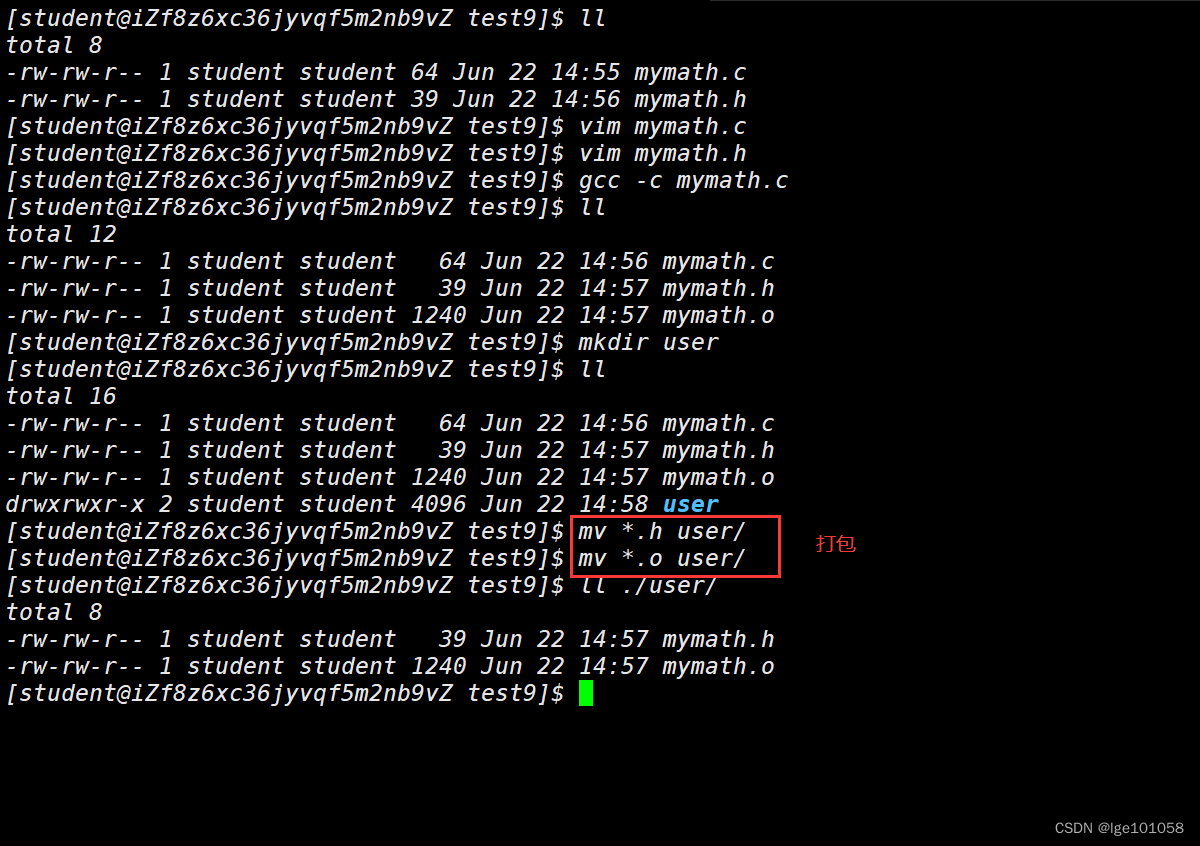
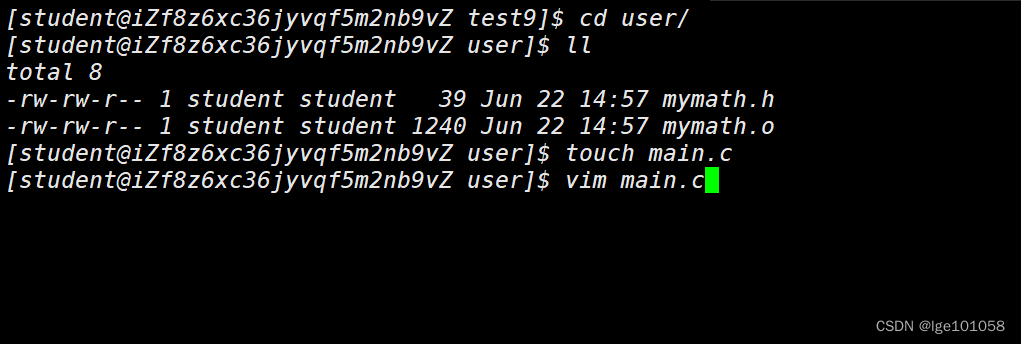
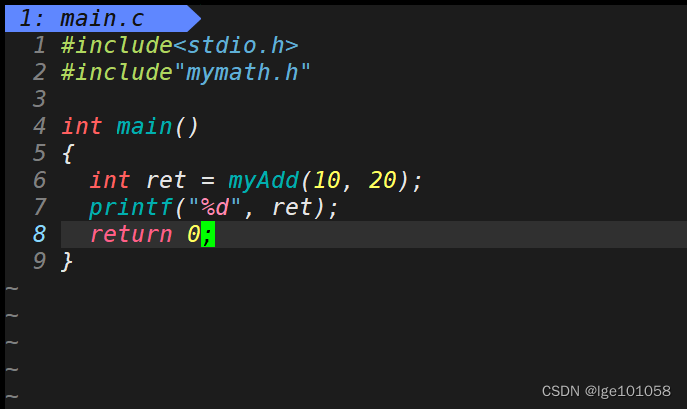
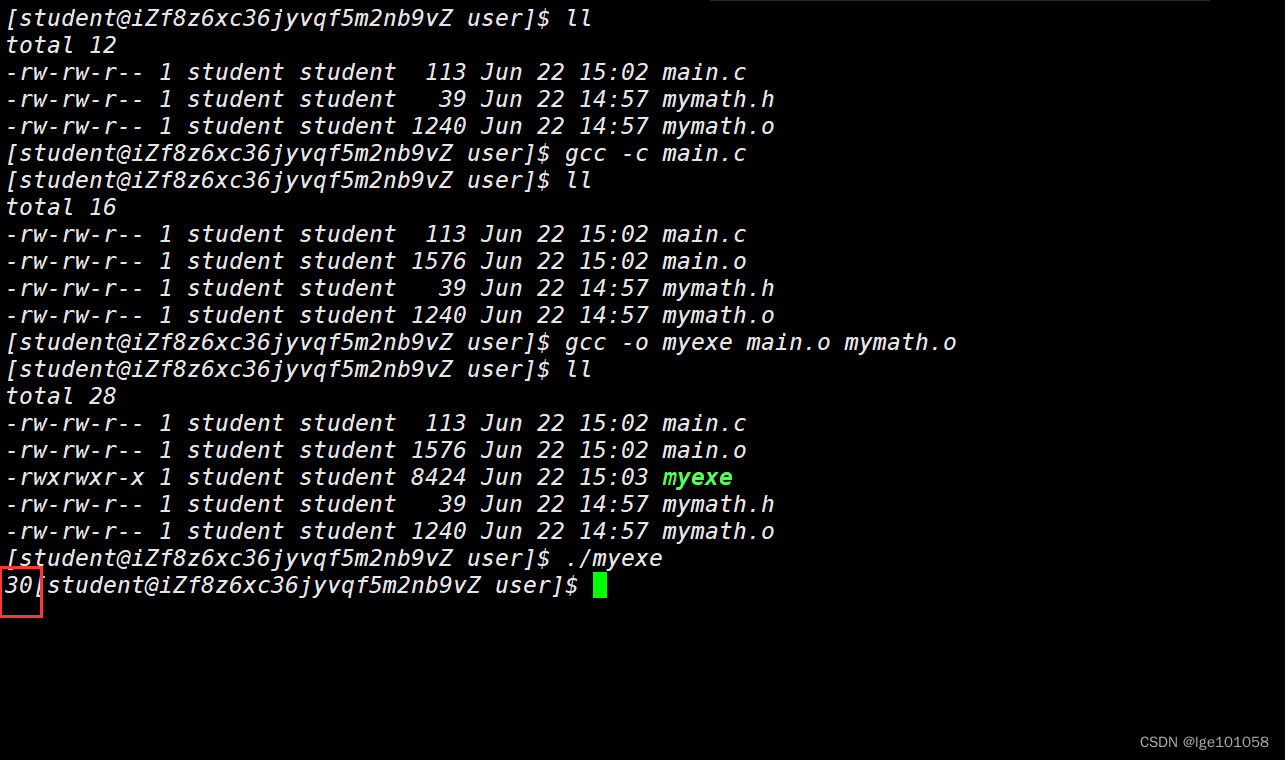
即便是我们没有实现 mymath 库中函数,我们同样可以用。
但是这里我们只是形式上打包了,并不是真正意义上的打包,这里我们来真正的创建一个库:
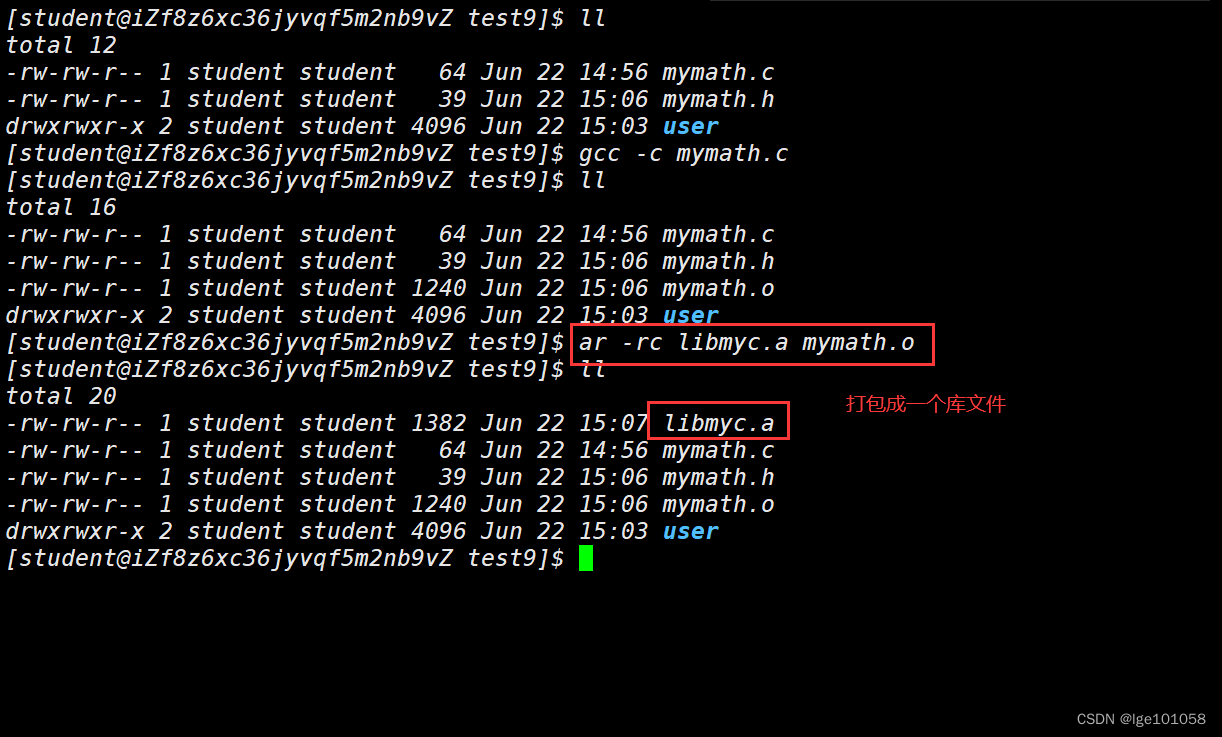
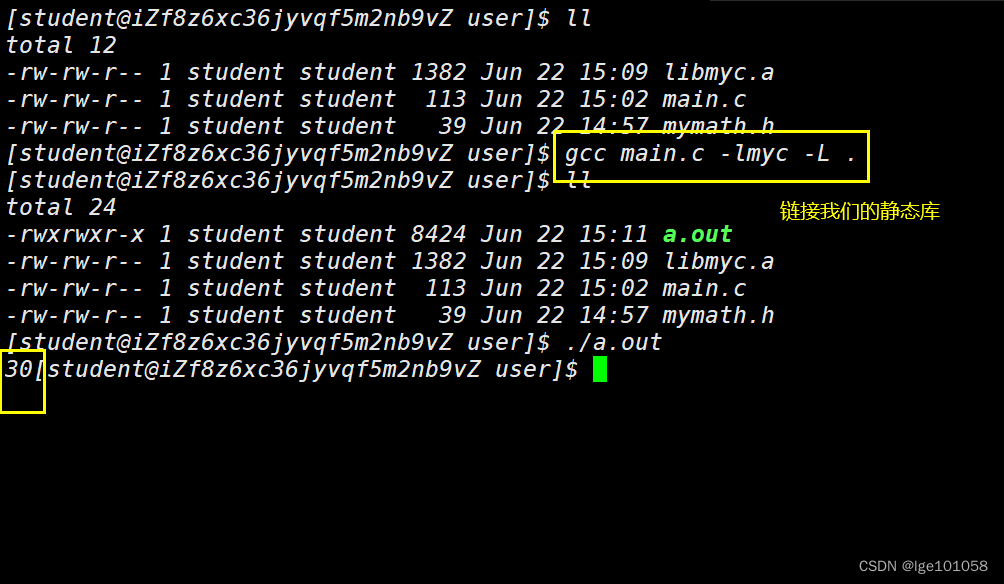
未完待续
相关文章:

【Linux】基础IO_3
文章目录 六、基础I/O3. 软硬链接4. 动静态库 未完待续 六、基础I/O 3. 软硬链接 使用 ln 就可以创建链接,使用 ln -s 可以创建软链接,直接使用 ln 则是硬链接。 我们对硬链接进行测试一下: 根据测试,我们知道了 硬链接就像一…...
ffmpeg音视频开发从入门到精通——ffmpeg实现音频抽取
文章目录 FFmpeg 实现音频流抽取1. 包含FFmpeg头文件与命名空间声明2. 主函数与参数处理3. 打开输入文件4. 获取文件信息5. 查找音频流6. 分配输出文件上下文7. 猜测输出文件格式8. 创建新的音频流9. 打开输出文件10. 写入文件头信息11. 读取并写入音频数据12. 写入文件尾部信息…...

计算机系统基础实训七-MallocLab实验
实验目的与要求 1、让学生理解动态内存分配的工作原理; 2、让学生应用指针、系统级编程的相关知识; 3、让学生应用各种动态内存分配器的实现方法; 实验原理与内容 (1)动态内存分配器基本原理 动态内存分配器维护…...
)
周末总结(2024/06/22)
工作 人际关系核心实践: 要学会随时回应别人的善意,执行时间控制在5分钟以内 坚持每天早会打招呼 遇到接不住的话题时拉低自己,抬高别人(无阴阳气息) 工作上的要点 现状(接受破烂现状,改变状态) - 这周没…...
【AI测试版】)
2024.06.22【读书笔记】丨生物信息学与功能基因组学(第十七章 人类基因组 第二部分)【AI测试版】
第二部分:人类基因组的主要结论与网络资源 摘要: 第二部分深入总结了人类基因组计划的关键发现,并介绍了用于探索人类基因组的网络资源。这些结论不仅为我们理解人类生物学提供了新的视角,而且揭示了人类基因组的复杂性和动态性。 学习目标: 掌握人类基因组计划的主要科…...

SpringCloud-nacos基础
SpringCloud-nacos nacos在微服务种有两大作用: 配置中心服务注册中心 配置中心 维度管理 nacos配置中心可以在三个维度进行管理: spring.profiles.active dev/prod/test,通过这个属性可以配置不同环境下的配置文件。 配置的文件名应该为${spring…...
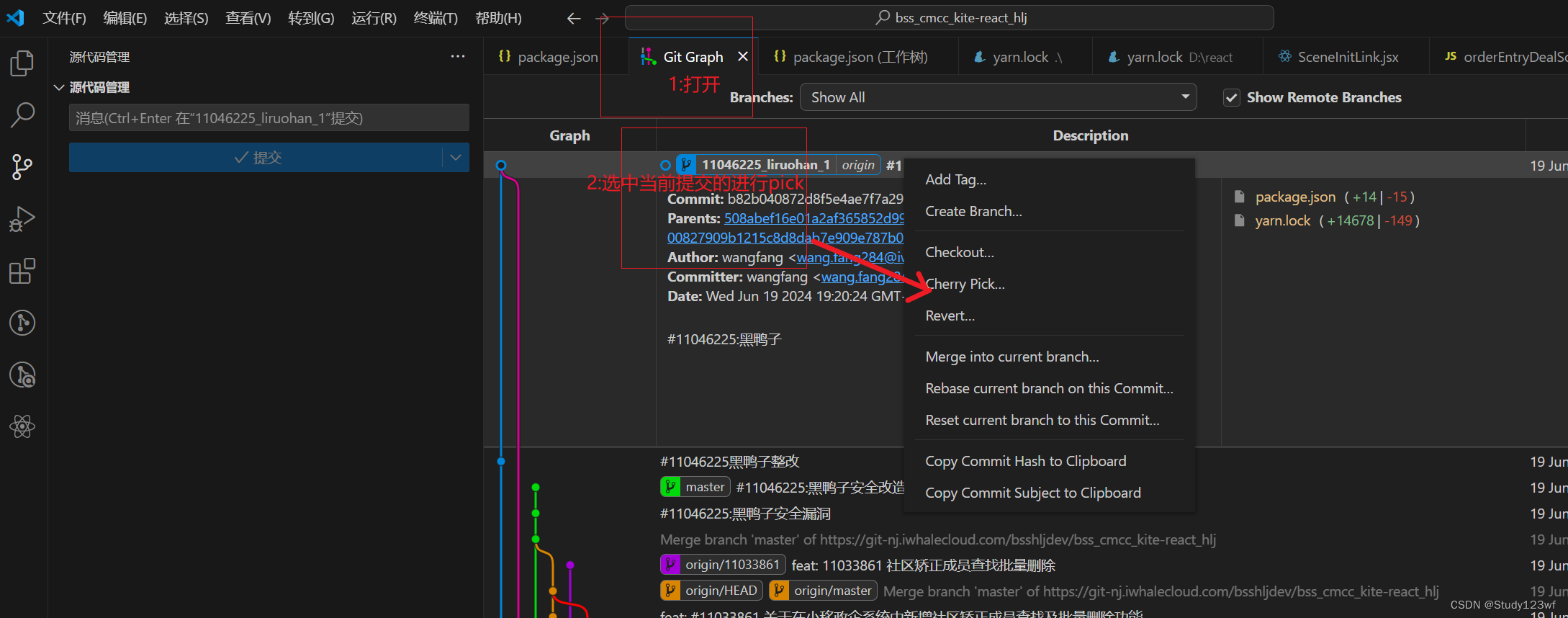
git的Cherry pick
Cherry pick Git Cherry Pick详解 https://blog.csdn.net/jam_yin/article/details/131594716 目标: 将开发分支A中提交的部分内容合并到B分支(可能是测试分支) 步骤: vscode安装 点击下图标进入graph...
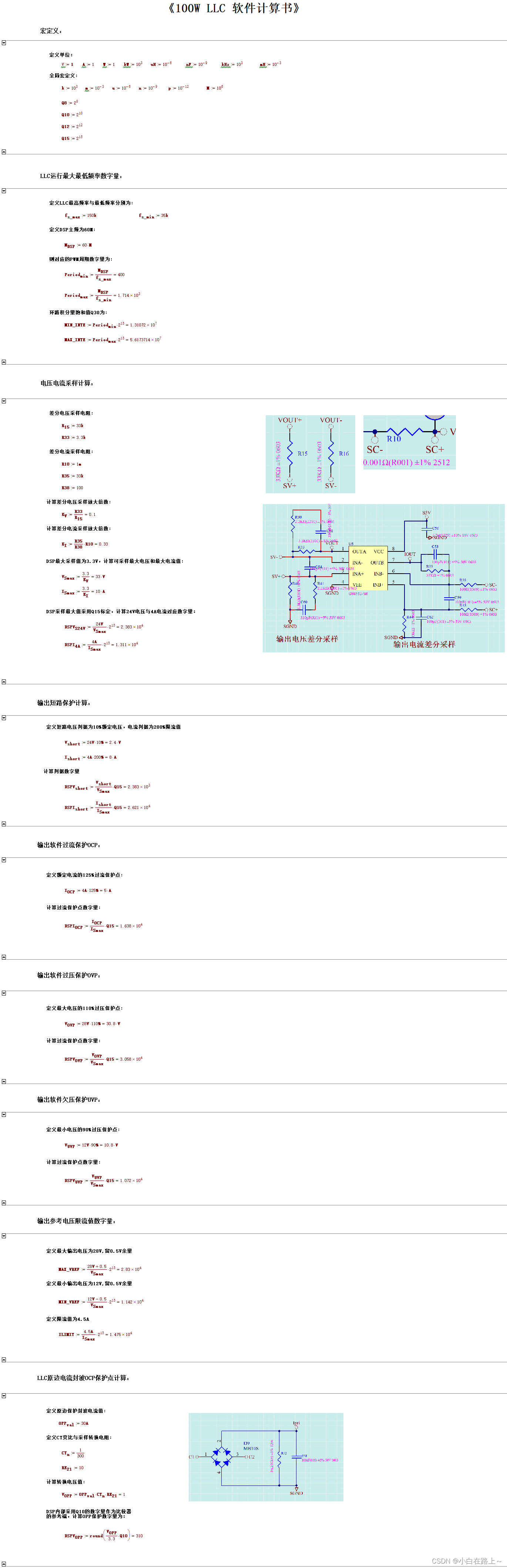
LLC开关电源开发:第四节,LLC软件设计报告
LLC源代码链接 数控全桥LLC开发板软件设计报告 1. LLC硬件及软件框架2. LLC软件设计2.1 工程文件说明2.2 LLC中断设计2.2.1 20us中断2.2.2 5ms中断 2.3 LLC状态机设计2.3.1 初始化状态2.3.2 空闲状态2.3.3 软启动状态2.3.4 正常运行状态2.3.5 故障状态 2.4 环路设计2.4.1 环路…...

力扣85.最大矩形
力扣85.最大矩形 遍历所有行作为底边 做求矩形面积(84. class Solution {public:int maximalRectangle(vector<vector<char>>& matrix) {if (matrix.empty()) return 0;int n matrix.size(),m matrix[0].size();int res0;vector<int> li…...

和琪宝的厦门之旅~
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 本作品 (李兆龙 博文, 由 李兆龙 创作),由 李兆龙 确认,转载请注明版权。 引言 承接去年国庆的遗憾,我们将这次的旅行城市定为厦门。 琪宝是下午四点左右到…...
4、MFC:菜单栏、工具栏与状态栏
菜单栏、工具栏与状态栏 1、菜单栏1.1 简介1.2 创建属性设置菜单消息成员函数 1.3 实例 2、工具栏2.1 简介工具栏属性2.2 创建消息CToolBar类的主要成员函数 2.3 实例 3、状态栏3.1 简介3.2 创建CStatusBar类状态栏创建 3.3 实例 1、菜单栏 1.1 简介 菜单在界面设计中是经常使…...

Java中的动态代理:原理与应用
Java中的动态代理:原理与应用 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 在Java开发中,动态代理是一种强大且灵活的技术ÿ…...

DataWhale - 吃瓜教程学习笔记(二)
学习视频:第3章-一元线性回归_哔哩哔哩_bilibili 西瓜书对应章节: 3.1 - 3.2 一元线性回归 - 最小二乘法 - 极大似然估计 - 梯度 多元函数的一阶导数 - 海塞矩阵 多元函数的二阶导数 - 机器学习三要素...
[保姆级教程]uniapp自定义标签页切换组件
文章目录 导文样式改成动态列表切换点击效果加上点击自动滑动scroll-view加上切换组件效果 导文 unaipp自带的标签页和ui设计相差太大,直接修改组件比手写一个还麻烦,下面手写一个。 样式 先用scroll-view做一个滑动,不然多的话滑动不了。 &l…...

4种典型家庭教育方式,无论开始是哪一种,都会过渡到最后一种
家庭教育,是孩子教育的一个重要组成部分,事实上是对孩子影响最大的一种教育方式,绝大部分家庭教育都是由孩子的父母来完成的。 家庭教育的特点 家庭教育具有很明显的启蒙性、长期性、全面性。 1.启蒙性。我们的孩子对外部世界的认识和了解&am…...
)
[Django学习]查询过滤器(lookup types)
1.exact exact用于精确匹配字段的值。适用于需要精确查找某个字段值的场景。 Book.objects.filter(title__exactHarry Potter) 上面的查询会查找标题完全为“Harry Potter”的书籍。 2.iexact iexact忽略大小写地精确匹配字段的值。适用于需要忽略大小写进行精确匹配的场…...
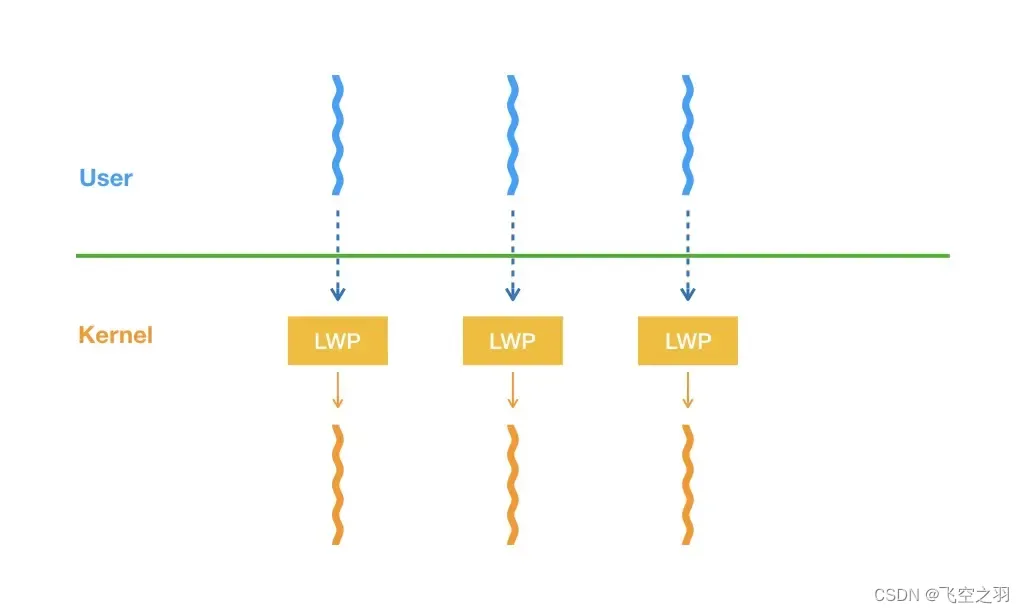
异步开发的终极答案—协程
我们在之前的文章中讲过,在并发场景下,传统的基于多线程的命令式开发模型虽然比较简单,但并发数高了之后资源占用较高,大量线程会阻塞;而响应式编程模式我们可以通过异步化处理提升系统资源的利用效率,但异步开发有违人的直觉,门槛比较高。作为成年人,我们肯定希望全都…...

构建高效的大数据量延迟任务调度平台
目录 引言系统需求分析系统架构设计 总体架构任务调度模块任务存储模块任务执行模块 任务调度算法 时间轮算法优先级队列分布式锁 数据存储方案 关系型数据库NoSQL数据库混合存储方案 容错和高可用性 主从复制数据备份与恢复故障转移 性能优化 水平扩展缓存机制异步处理 监控与…...
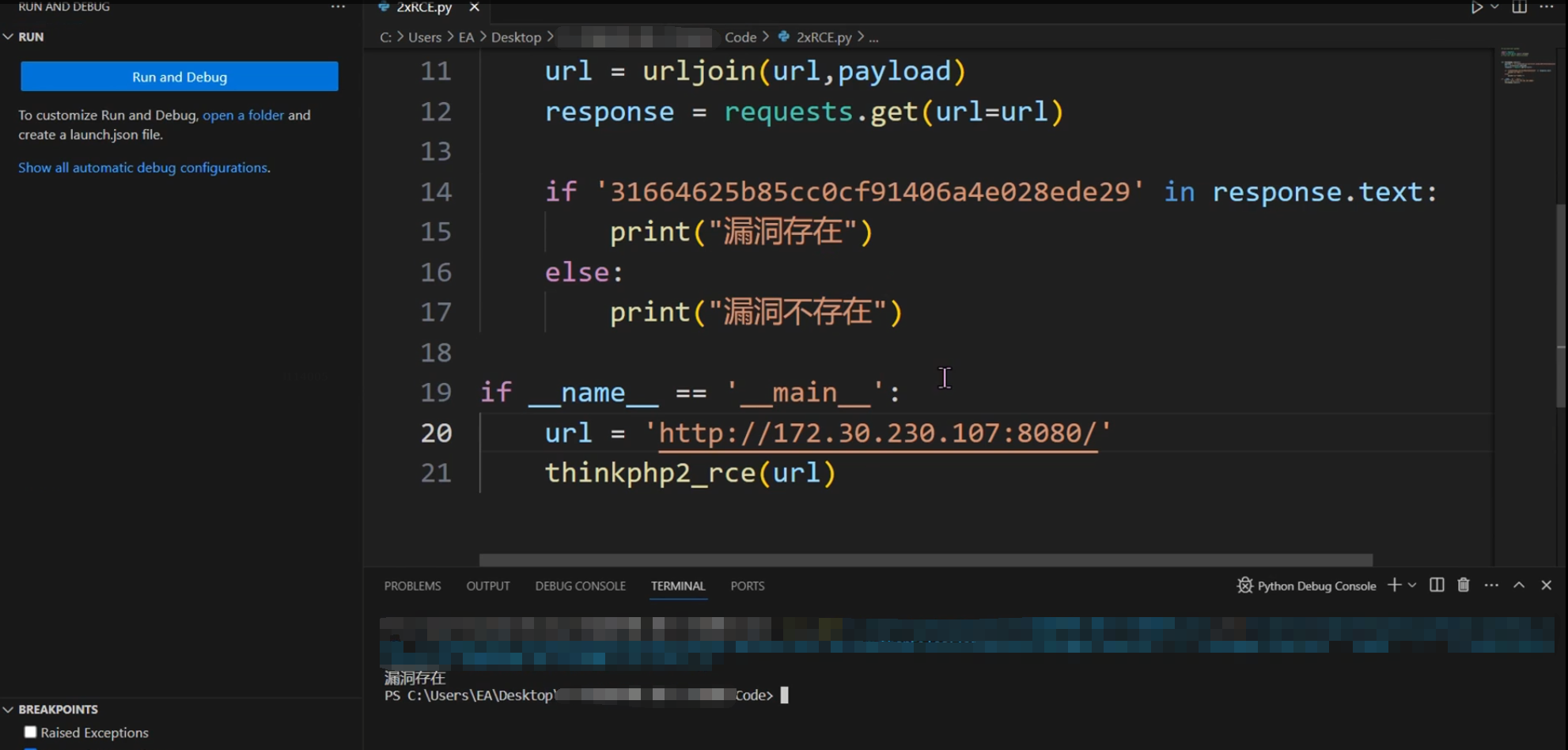
Python武器库开发-武器库篇之ThinkPHP 2.x 任意代码执行漏洞(六十三)
Python武器库开发-武器库篇之ThinkPHP 2.x 任意代码执行漏洞(六十三) PHP代码审计简介 PHP代码审计是指对PHP程序进行安全审计,以发现潜在的安全漏洞和风险。PHP是一种流行的服务器端脚本语言,广泛用于开发网站和Web应用程序。由…...

SQLite数据库(数据库和链表双向转换)
文章目录 SQLite数据库一、SQLite简介1、SQLite和MySQL2、基于嵌入式的数据库 二、SQLite数据库安装三、SQLite的常用命令四、SQLite的编程操作1、SQLite数据库相关API(1)头文件(2)sqlite3_open()(3)sqlite…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
