MATLAB复习
MATLAB常用的标点符号
| 空格 | 变量分隔符 矩阵一行中各元素间的分隔符 | |
| 逗号 | ， | 分隔显示计算结果的各语句 变量分隔符 矩阵中一行各元素的分隔符 |
| 点号 | . | 数值中的小数点 结构数组的域访问符 |
| 分号 | ； | 分隔不想显示计算结果的各语句 矩阵行与行的分隔符 |
| 冒号 | ： | 用于生成一维数值数组 表示一维数组的全部元素或多维数组某一维的全部元素 |
| 百分号 | % | 注释语句说明符，凡在其后的字符均视为注释性内容而不被执行 |
| 单引号 | ' ' | 字符串标识符 |
| 圆括号 | () | 用于矩阵元素引用 用于函数输入变量列表 确定运算的先后次序 |
| 方括号 | [ ] | 向量和矩阵标识符 用于函数输出列表 |
| 花括号 | {} | 标识细胞数组 |
| 续行符 | ... | 长命令行需分行时连接下行用 |
| 赋值号 | = | 表达式赋值给一个变量6 |
逗号
显示计算结果的指令与其后指令的分隔
用作输入量与输入量的分隔符
用作数组元素分隔符号
命令行窗口清屏 clc 清除指令窗中显示的内容
清除MATLAB工作空间的所有变量clear
清除图形窗clf
whos
变量命名规则
（1）变量名称和函数名称有大小写之分
（2）变量名称的第一个字符必须是英文字符
5xf、_mat等都是不合法的变量名称
（3）变量名称中不可以包含空格或者标点符号，但是可以包含下划线
xf_mat是合法的
MATLAB文件存取的命令
save Filename
load Filename
MATLAB中的预定义变量
| ans | 计算结果的默认名称 |
| eps | 计算机的零阈值 |
| Inf(inf) | A无穷大 |
| pi | 圆周率 |
| NaN（nan） | 表示结果或者变量不是数值 0/0 0*∞ ∞/∞ |
MATLAB中的取整函数
| round(a) | 向最接近的整数取整，小数 部分是0.5时向绝对值大的方向取整 |
| fix(a) | 向0方向取整 |
| floor(a) | 向不大于a的最接近整数取整 |
| ceil(a) | 向不小于a的最接近整数取整 |
复数相关运算函数
| real(z) | 返回复数z的实部 |
| imag(z) | 虚部 |
| abs(z) | 幅度 |
| angle(z) | 幅角 |
| conj(z) | 共轭复数 |
| complex(a,b) | 以a为实部、b为虚部创建复数 |
A=[2,3,4,5,6]
A=1:2:10 %1 3 5 7 9
A=linspace(1,30,5)
%1.0000 8.2500 15.5000 22.7500 30.0000
向量的点积运算：对应位置上的元素相乘然后再相加
dot(A)
叉积运算：A、B的叉积C，C的方向垂直于A与B所确定的平面
cross(A)
矩阵元素的下标表示法
（1）全下标A(i,j)
（2）单下标A(s) s=(j-1)*m+i
A(2,3) A(6)
A(1:2,3) 矩阵A第1、2行第3列的元素值
A(6,8) 矩阵A单下标第6-8号元素的值
A(:)=1:9
A=
1 4 7
2 5 8
3 6 9
A(2,:)=[ ] %删除第二行
矩阵的创建
- 直接输入法
- 抽取法
A=[1 2 3 4;5 6 7 8;9 10 11 12;13 14 15 16]
A=
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
（1）全下标
B=A(1:3,2:3) %取矩阵A行数为1~3、列数为2~3的元素构成子矩阵B
B=
2 3
6 7
10 11
C=A([1,3],[2,4]) %取矩阵A行数为1、3，列数为2、4的元素构成子矩阵C
C=
2 4
10 12
D=A(4,:) %取矩阵A的第4行、所有列
D=
13 14 15 16
（2）单下标
B=A([4:6;3 5 7;12:14])
B=
13 2 6
9 2 10
15 4 8
- 拼接法
F=[A;C]
- 函数法
矩阵生成函数
| zeros(m,n) | 生成m*n阶的全0矩阵 |
| ones(m,n) | 全1矩阵 |
| rand(m,n) | 生成取值在0~1之间满足均匀分布的随机矩阵 |
| randn(m,n) | 生成满足正态分布的随机矩阵 |
| eye(m,n) | 生成m*n阶的单位矩阵 |
相关文章：
MATLAB复习
MATLAB常用的标点符号 空格 变量分隔符 矩阵一行中各元素间的分隔符 程序语句关键词分隔符 逗号，分隔显示计算结果的各语句 变量分隔符 矩阵中一行各元素的分隔符点号.数值中的小数点 结构数组的域访问符分号；分隔不想显示计算结果的各语句 矩阵行与行的…...
Android11 动态权限申请
1、单个权限检查及申请 private void checkSinglePermission(){// 在需要的地方，如Activity中if (ContextCompat.checkSelfPermission(this, Manifest.permission.READ_PHONE_STATE)! PackageManager.PERMISSION_GRANTED) {ActivityCompat.requestPermissions(this,…...
线性卷积（相关）和圆周卷积（相关）以及FFT之间的关系(AEC举例)
时域自适应滤波算法中的线性卷积和线性相关运算量较大，导致计算复杂度升高，我们更愿意把这两个信号变换到频域，通过频域相乘的方式来取代时域复杂度相当高的卷积或相关运算。 预备知识：线性卷积（相关）和圆…...
AMD平台，5600X+6650XT，虚拟机安装macOS 14(2024年6月)
AMD平台安装macOS 14的麻烦，要比Intel平台多的多，由于macOS从13开始，对CPU寄存器的读取进行了改变，导致AMD平台只要安装完macOS 13及以后版本，开机后就报五国语言错误，不断重启。改vmx文件，被证…...
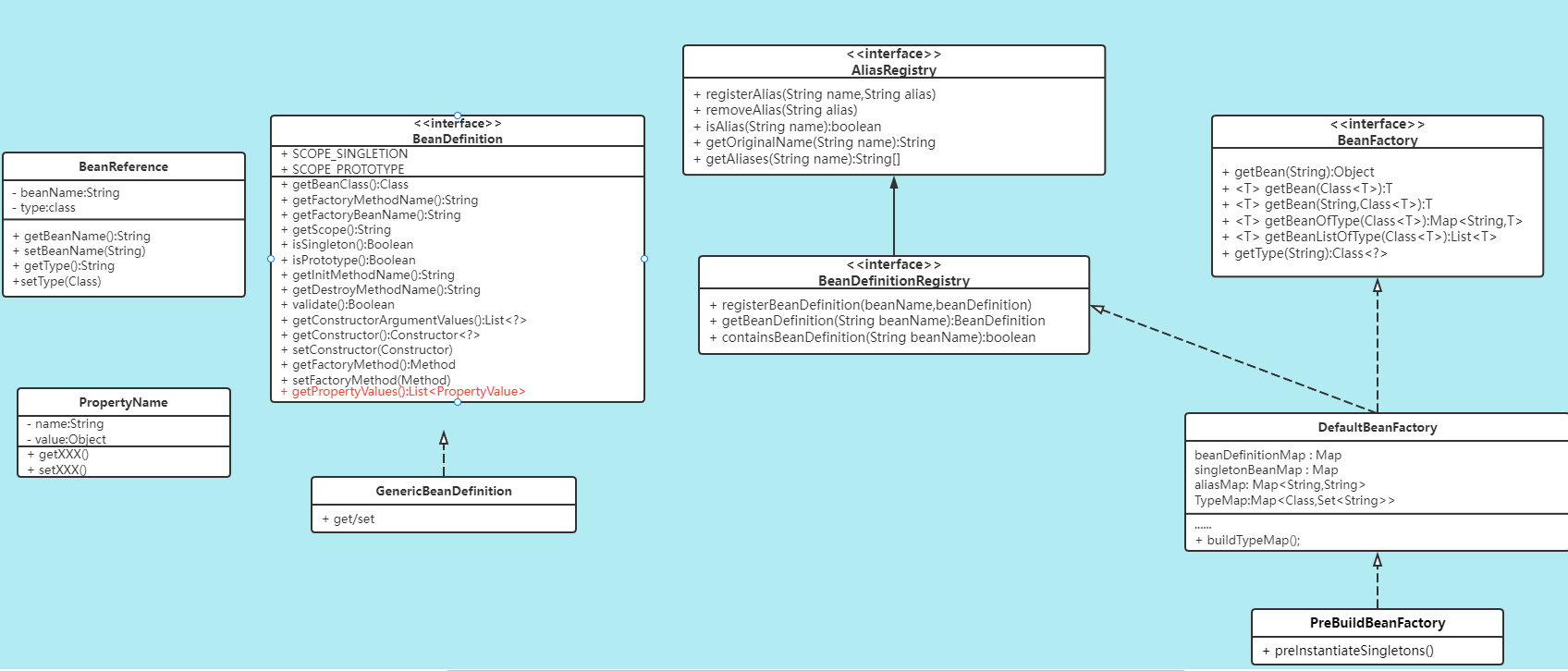
Spring源码之手写DI
Spring源码之手写DI 我们来回顾一下前面手写IOC的内容。 一、DI介绍 DI(Dependency injection)依赖注入。对象之间的依赖由容器在运行期决定，即容器动态的将某个依赖注入到对象之中。说直白点就是给Bean对象的成员变量赋值。 在这里我们就需要明白几个问题。 1.…...
从零入手人工智能（5）—— 决策树
1.前言 在上一篇文章《从零入手人工智能（4）—— 逻辑回归》中讲述了逻辑回归这个分类算法，今天我们的主角是决策树。决策树和逻辑回归这两种算法都属于分类算法，以下是决策树和逻辑回归的相同点： 分类任务࿱…...
go语言：两协程并发交替打印数字和字母（代码逐行注释）
要求： 并发两协程交替打印数字和字母。一个协程打印数字，一个协程打印字母。 输出： 12AB34CD56EF78GH910IJ1112KL1314MN1516OP1718QR1920ST2122UV2324WX2526YZ2728 思路： 两个 channel 控制两个协程进行交替打印。sync.WaitG…...
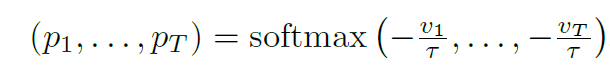
TWM论文阅读笔记
这是ICLR2023的一篇world model论文，用transformer来做世界模型的sequence prediction。文章贡献是transformer-based world model（不同于以往的如transdreamer的world model，本文的transformer-based world model在inference 的时候可以丢掉…...
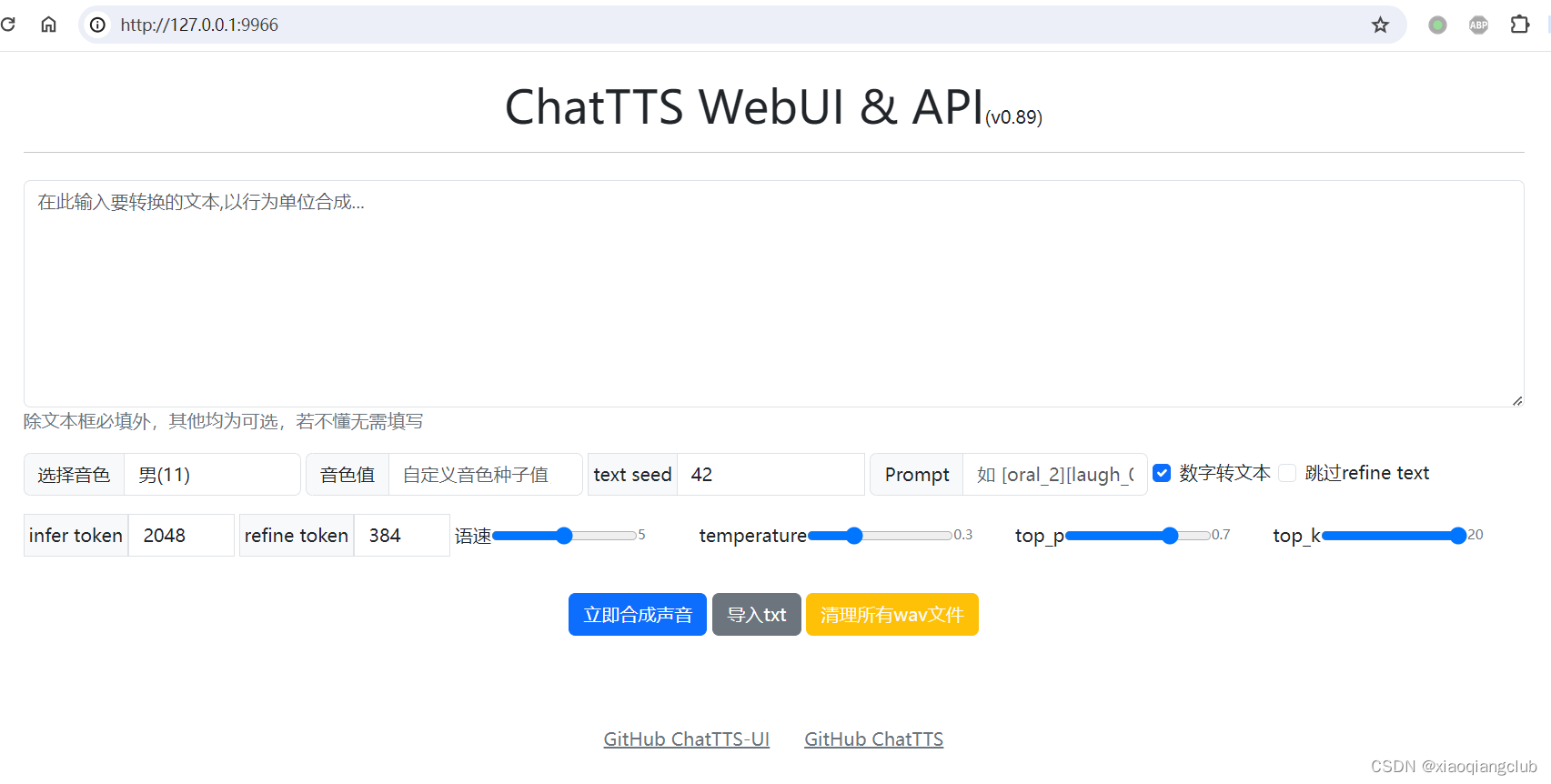
探索ChatTTS项目：高效的文字转语音解决方案
文章目录 📖 介绍 📖📒 ChatTTS 📒📝 项目介绍📝 项目亮点📝 UI 🎈 项目地址 🎈 📖 介绍 📖 在AI技术迅速发展的今天，文本到语音&…...
[Django学习]Q对象实现多字段模糊搜索
一、应用场景 假设我们现在有一个客房系统,前端界面上展示出来了所有客房的所有信息。用户通过客房的价格、面积、人数等对客房进行模糊搜索，如检索出价格在50到100元之间的客房，同时检索面积在20平方米到30平方米之间的客房，此时后端可以借助…...
transdreamer 论文阅读笔记
这篇文章是对dreamer系列的改进，是一篇world model 的论文改进点在于，dreamer用的是循环神经网络，本文想把它改成transformer，并且希望能利用transformer实现并行训练。改成transformer的话有个地方要改掉，dreamer用ht…...
AIGC技术的发展现状与未来趋势探讨
AIGC技术的发展现状与未来趋势探讨 随着人工智能（AI）技术的迅猛发展，AI生成内容（AI-Generated Content，AIGC）成为了一项颠覆性的技术，它能够自动生成文本、图像、音频和视频等多种内容。本文将…...
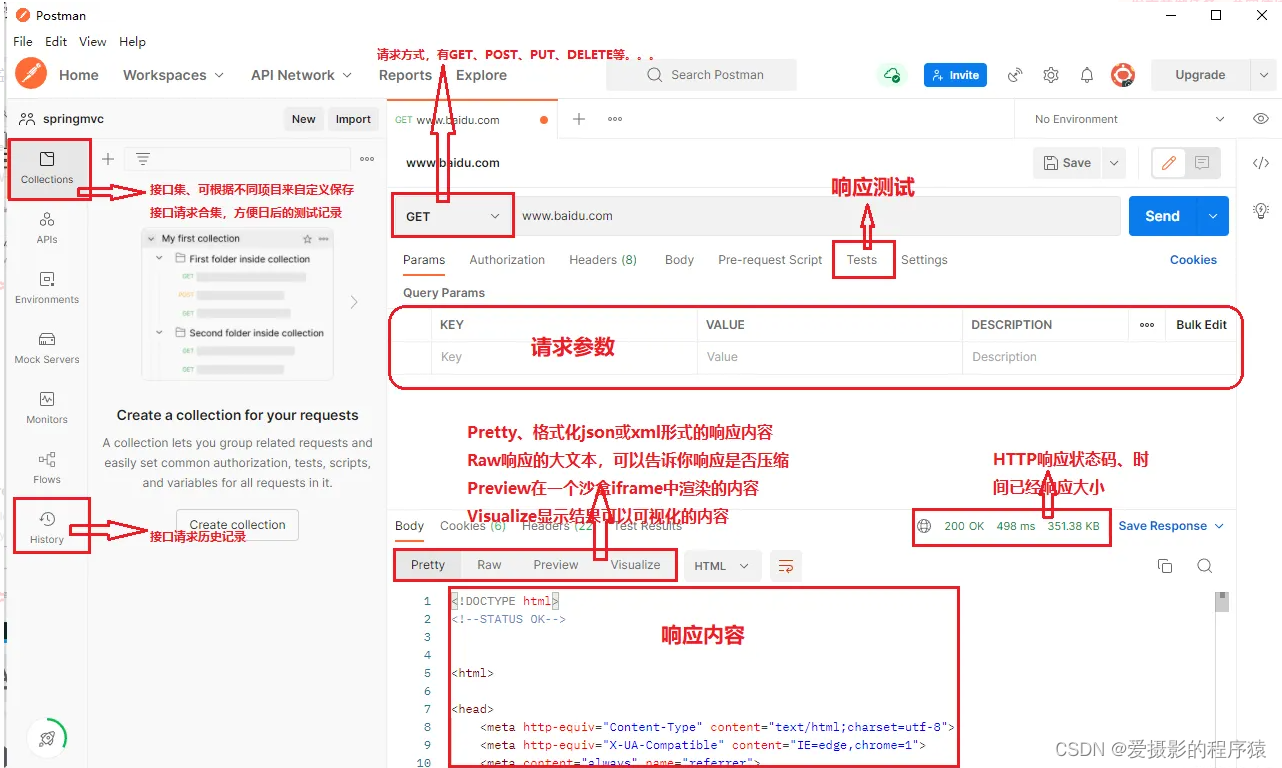
Postman Postman接口测试工具使用简介
Postman这个接口测试工具的使用做个简单的介绍，仅供参考。 插件安装 1）下载并安装chrome浏览器 2）如下 软件使用说明...
Java开发笔记Ⅱ（Jsoup爬虫）
Jsoup 爬虫 Java 也能写爬虫！！！ Jsoup重要对象如下： Document：文档对象，每个html页面都是一个Document对象 Element：元素对象，一个Document对象里有多个Element对象 Node&#…...
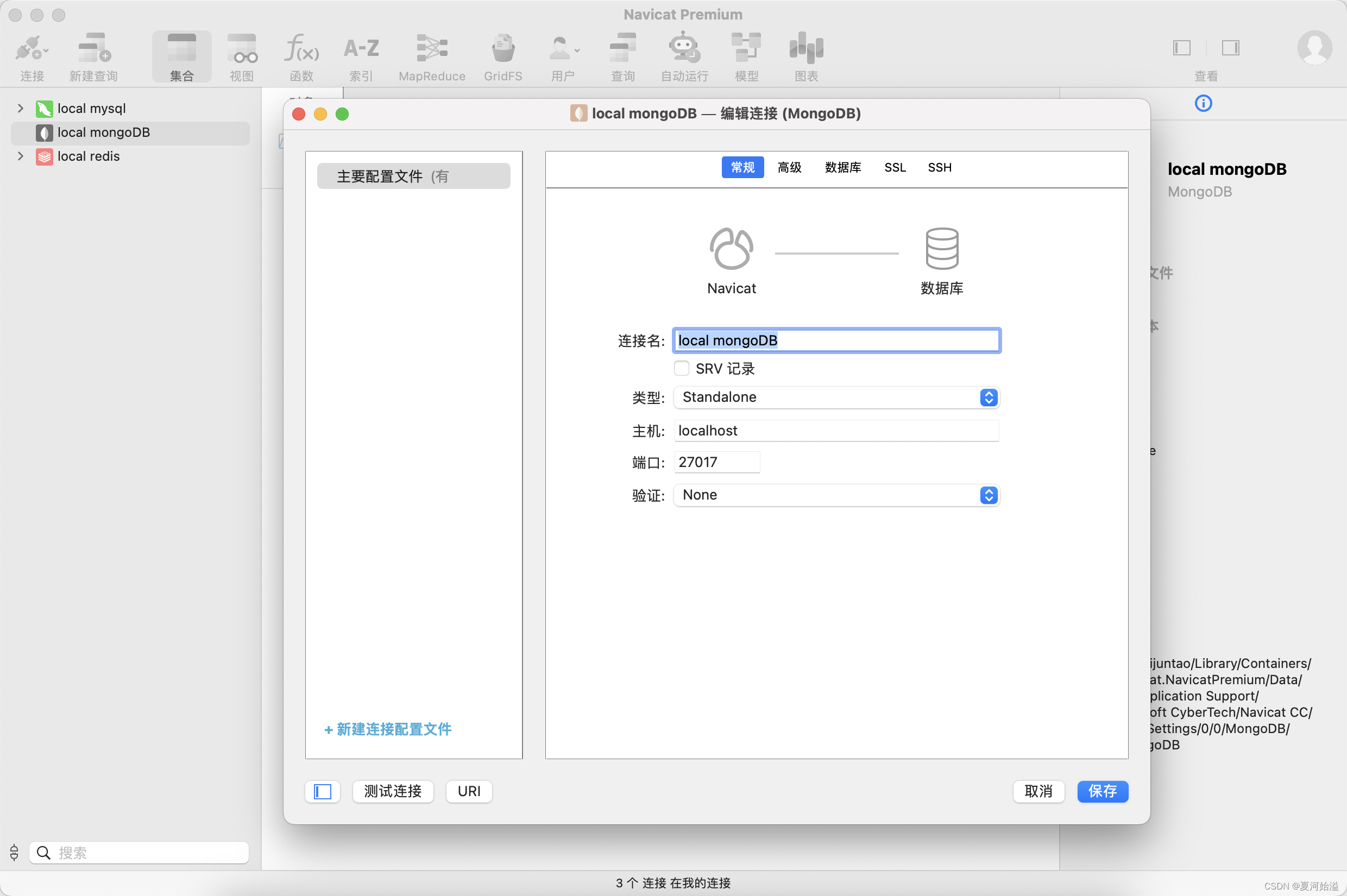
一五三、MAC 安装MongoDB可视化工具连接
若没有安装brew包管理工具，在命令行输入安装命令 /bin/bash -c “$(curl -fsSL https://gitee.com/cunkai/HomebrewCN/raw/master/Homebrew.sh)”上面步骤安装完成后，开始安装MongoDB，输入安装命令： brew tap mongodb/brewbrew u…...
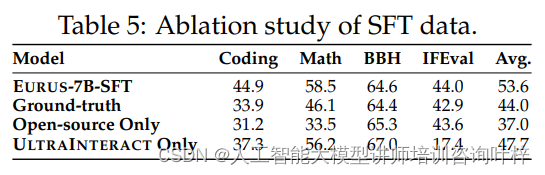
ULTRAINTERACT 数据集与 EURUS 模型：推动开源大型语言模型在推理领域的新进展
在人工智能的浪潮中，大型语言模型（LLMs）已经成为推动自然语言处理技术发展的关键力量。它们在理解、生成语言以及执行复杂任务方面展现出了巨大的潜力。然而，尽管在特定领域内取得了显著进展，现有的开源LLMs在处理多样…...
【leetcode刷题】面试经典150题 , 27. 移除元素
leetcode刷题 面试经典150 27. 移除元素 难度：简单 文章目录 一、题目内容二、自己实现代码2.1 方法一：直接硬找2.1.1 实现思路2.1.2 实现代码2.1.3 结果分析 2.2 方法二：排序整体删除再补充2.1.1 实现思路2.1.2 实现代码2.1.3 结果分析 三、…...
红队内网攻防渗透：内网渗透之内网对抗：横向移动篇PTH哈希PTT票据PTK密匙Kerberoast攻击点TGTNTLM爆破
红队内网攻防渗透 1. 内网横向移动1.1 首要知识点1.2 PTH1.2.1 利用思路第1种：利用直接的Hash传递1.2.1.1、Mimikatz1.2.2 利用思路第2种：利用hash转成ptt传递1.2.3 利用思路第3种：利用hash进行暴力猜解明文1.2.4 利用思路第4种：修改注册表重启进行获取明文1.3 PTT1.3.1、漏…...
springBoot不同module之间互相依赖
在 Spring Boot 多模块项目中，不同模块之间的依赖通常是通过 Maven 或 Gradle 来管理的。以下是一个示例结构和如何设置这些依赖的示例。 项目结构 假设我们有一个多模块的 Spring Boot 项目，结构如下： my-springboot-project │ ├── p…...
[modern c++] 类型萃取 type_traits
前言： #include <type_traits> type_traits 又叫类型萃取，是一个在编译阶段用于进行 类型判断/类型变更 的库，在c11中引入。因为其工作阶段是在编译阶段，因此被大量应用在模板编程中，同时也可以结合 constexpr…...
C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中，我们已经大致实现了rpc服务端的各项功能代…...
Auto-Coder使用GPT-4o完成：在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库，获取股票数据，并生成TabPFN这个模型 可以识别、处理的格式，写一个完整的预处理示例，并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务，进行预测并输…...
2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...
《用户共鸣指数（E）驱动品牌大模型种草：如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代，情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现，消费者对内容的“有感”程度，正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...
UR 协作机器人「三剑客」：精密轻量担当（UR7e）、全能协作主力（UR12e）、重型任务专家（UR15）
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中，UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...
Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章，二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑： 🔄 一、起源与初创期：Swagger的诞生（2010-2014） 核心…...
保姆级教程：在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama（有网络的电脑）2.2.3 安装Ollama（无网络的电脑）2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...
LangChain知识库管理后端接口：数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块，用于对本地知识库系统中的知识库进行增删改查（CRUD）操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...
go 里面的指针
指针 在 Go 中，指针（pointer）是一个变量的内存地址，就像 C 语言那样： a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10，通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...
ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件，可以展示文件夹，支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项，适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...