如何利用AopContext.currentProxy()解决事务管理中的方法调用问题
在Spring应用开发中,使用AOP(面向切面编程)来管理事务是非常常见的做法。然而,在某些场景下,尤其是在同一个类的方法内部,一个非事务方法直接调用另一个带有事务注解的方法时,可能会遇到事务不生效的问题。本文将深入探讨这一问题的原因,并介绍如何通过AopContext.currentProxy()方法来有效解决这一问题。
问题背景
想象一下,你有一个服务类UserService,其中包含两个方法:saveUser()需要事务支持来保证数据的一致性,而processUser()作为一个业务处理逻辑,它直接调用了saveUser()方法,但未被标记为事务方法。
引入AspectJ依赖:
<!--aspecj-->
<dependency><groupId>org.aspectj</groupId><artifactId>aspectjweaver</artifactId>
</dependency>
@Service
public class UserService {@Transactionalpublic void saveUser(User user) {// 保存用户逻辑}public void processUser(User user) {// 预处理逻辑saveUser(user); // 直接调用,期望saveUser的事务生效// 后处理逻辑}
}
== 在这种情况下==,你会发现当saveUser()方法中抛出异常时,事务并未回滚,这是因为Spring AOP的代理机制仅对外部调用生效。直接在类内部方法间调用时,事务注解并不会被Spring的代理所识别,导致事务失效。
解决方案:使用AopContext.currentProxy()
为了解决上述问题,可以利用Spring提供的AopContext.currentProxy()方法来获取当前类的代理对象,并通过该代理对象来调用事务方法,从而确保事务的正常工作。
首先,确保你的类是Spring管理的bean,并且运行在Spring的代理模式下(默认是基于JDK动态代理的)。接着,修改processUser()方法,使用AopContext.currentProxy()来间接调用saveUser()。
@Service
public class UserService {private UserService userService;@Transactionalpublic void saveUser(User user) {// 保存用户逻辑}public void processUser(User user) {try {((UserService) AopContext.currentProxy()).saveUser(user);} catch (Exception e) {// 异常处理}// 后处理逻辑}
}
注意
@EnableAspectJAutoProxy(exposeProxy = true)
@SpringBootApplication
public class Application {
}
关键步骤解析。
使用代理对象调用事务方法:在processUser()方法中,使用(UserService) AopContext.currentProxy()获取当前线程的代理对象,并通过这个代理对象调用saveUser()。这样,事务管理器就能识别到事务边界,确保事务正常生效。
通过上述方法,我们有效地解决了Spring AOP中因内部方法调用导致事务失效的问题,保证了业务逻辑的正确性和数据的一致性。
相关文章:
解决事务管理中的方法调用问题)
如何利用AopContext.currentProxy()解决事务管理中的方法调用问题
在Spring应用开发中,使用AOP(面向切面编程)来管理事务是非常常见的做法。然而,在某些场景下,尤其是在同一个类的方法内部,一个非事务方法直接调用另一个带有事务注解的方法时,可能会遇到事务不生…...
VMware虚拟机下载安装Windows Server 2016
「作者简介」:2022年北京冬奥会网络安全中国代表队,CSDN Top100,就职奇安信多年,以实战工作为基础对安全知识体系进行总结与归纳,著作适用于快速入门的 《网络安全自学教程》,内容涵盖系统安全、信息收集等…...
springboot vue 开源 会员收银系统 (7) 收银台的完善 新增开卡 结算
前言 完整版演示 开发版演示 在前面的开发中,我们成功完成了商品分类和商品信息的搭建,开发了收银台基础。现在,我们将进一步完善收银台的功能,添加开卡和结算功能,并在后台实现会员卡的创建和订单保存。同时ÿ…...
虚拟现实环境下的远程教育和智能评估系统(十三)
管理/教师端前端工作汇总education-admin: 首先是登录注册页面的展示 管理员 首页 管理员登录后的首页如下图所示 管理员拥有所有的权限 课程管理 1、可以查看、修改、增添、删除课程列表内容 2、可以对课程资源进行操作 3、可以对课程的类别信息进行管理&…...

深入了解软件设计模式:创新应用与优化代码结构
前言 在软件开发中,设计模式被广泛应用,通常分为三大类:创建型、结构型和行为型。这些模式经过时间验证,在解决特定问题和优化代码结构方面发挥了重要作用。本文将详细介绍每一类设计模式,并通过具体实例展示它们的应…...
android studio 模拟器文件查找
android studio 模拟器文件查找 使用安卓模拟器下载文件后通常无法在系统硬盘上找到下载的文件,安卓 studio studio 其实提供了文件浏览工具,找到后可以直接使用 Android studio 打开 打开 Android studioview 菜单view > Tool Windows > Device…...
【科普】半导体制造过程的步骤、技术、流程
在这篇文章中,我们将学习基本的半导体制造过程。为了将晶圆转化为半导体芯片,它需要经历一系列复杂的制造过程,包括氧化、光刻、刻蚀、沉积、离子注入、金属布线、电气检测和封装等。 基本的半导体制造过程 1.晶圆(Wafer…...

c89、c99、c11
C99 标准开始引入了 // 单行注释。在此之前,C语言只支持 /* ... */ 多行注释。 具体说明: // 单行注释:在C99标准(ISO/IEC 9899:1999)引入之前,C语言中没有单行注释。C99标准借鉴了C的注释风格࿰…...
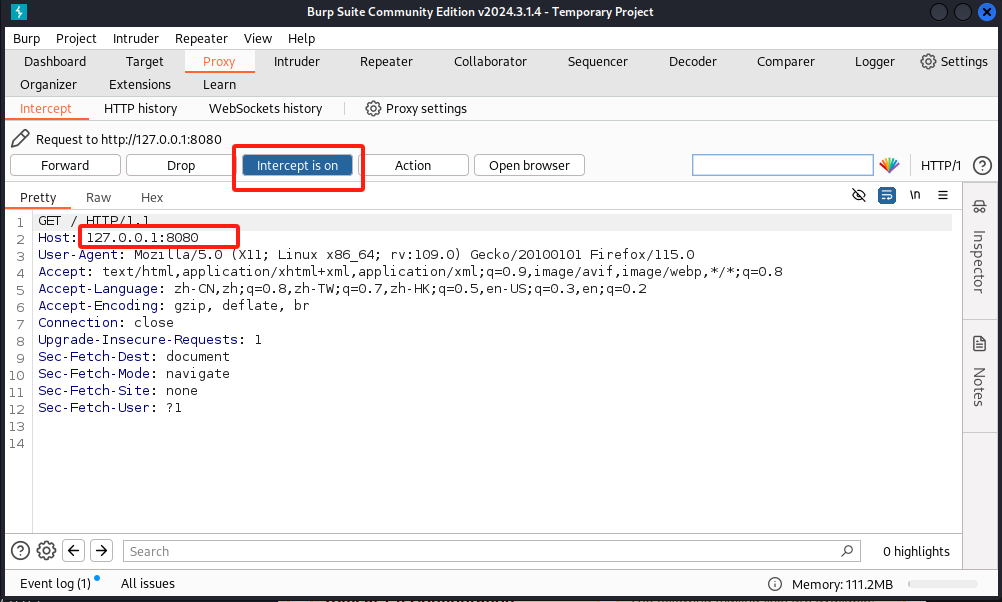
【网络安全的神秘世界】已解决burpsuite报错Failed to start proxy service on 127.0.0.1:8080
🌝博客主页:泥菩萨 💖专栏:Linux探索之旅 | 网络安全的神秘世界 | 专接本 | 每天学会一个渗透测试工具 解决burpsuite无法在 127.0.0.1:8080 上启动代理服务端口被占用以及抓不到本地包的问题 Burpsuite无法启动proxy…...

【C#】使用数字和时间方法ToString()格式化输出字符串显示
在C#编程项目开发中,几乎所有对象都有格式化字符串方法,其中常见的是数字和时间的格式化输出多少不一样,按实际需要而定吧,现记录如下,以后会用得上。 文章目录 数字格式化时间格式化 数字格式化 例如,保留…...

Mac系统主机名变为bogon的解决方案
如题 在使用Mac操作系统时,您可能会遇到一个有趣且略显困扰的问题:终端中显示的主机名突然变成了“bogon”。这不仅让人困惑,还可能给日常操作带来不便。本文旨在提供一种简便的解决方法,帮助您将主机名恢复为正常状态。 什么是…...

行列式和矩阵的区别
目录 一、行列式 1. 行列式的定义 2. (全)排列 3. 逆序数 二、矩阵 1. 矩阵的定义 三、行列式和矩阵的区别 四、参考书目 一、行列式 1. 行列式的定义 2. (全)排列 3. 逆序数 二、矩阵 1. 矩阵的定义 三、行列式和矩阵的区别 四、参考书目 同济大学数学系. 工程数学…...

MATLAB复习
MATLAB常用的标点符号 空格 变量分隔符 矩阵一行中各元素间的分隔符 程序语句关键词分隔符 逗号,分隔显示计算结果的各语句 变量分隔符 矩阵中一行各元素的分隔符点号.数值中的小数点 结构数组的域访问符分号;分隔不想显示计算结果的各语句 矩阵行与行的…...

Android11 动态权限申请
1、单个权限检查及申请 private void checkSinglePermission(){// 在需要的地方,如Activity中if (ContextCompat.checkSelfPermission(this, Manifest.permission.READ_PHONE_STATE)! PackageManager.PERMISSION_GRANTED) {ActivityCompat.requestPermissions(this,…...

线性卷积(相关)和圆周卷积(相关)以及FFT之间的关系(AEC举例)
时域自适应滤波算法中的线性卷积和线性相关运算量较大,导致计算复杂度升高,我们更愿意把这两个信号变换到频域,通过频域相乘的方式来取代时域复杂度相当高的卷积或相关运算。 预备知识:线性卷积(相关)和圆…...
AMD平台,5600X+6650XT,虚拟机安装macOS 14(2024年6月)
AMD平台安装macOS 14的麻烦,要比Intel平台多的多,由于macOS从13开始,对CPU寄存器的读取进行了改变,导致AMD平台只要安装完macOS 13及以后版本,开机后就报五国语言错误,不断重启。改vmx文件,被证…...
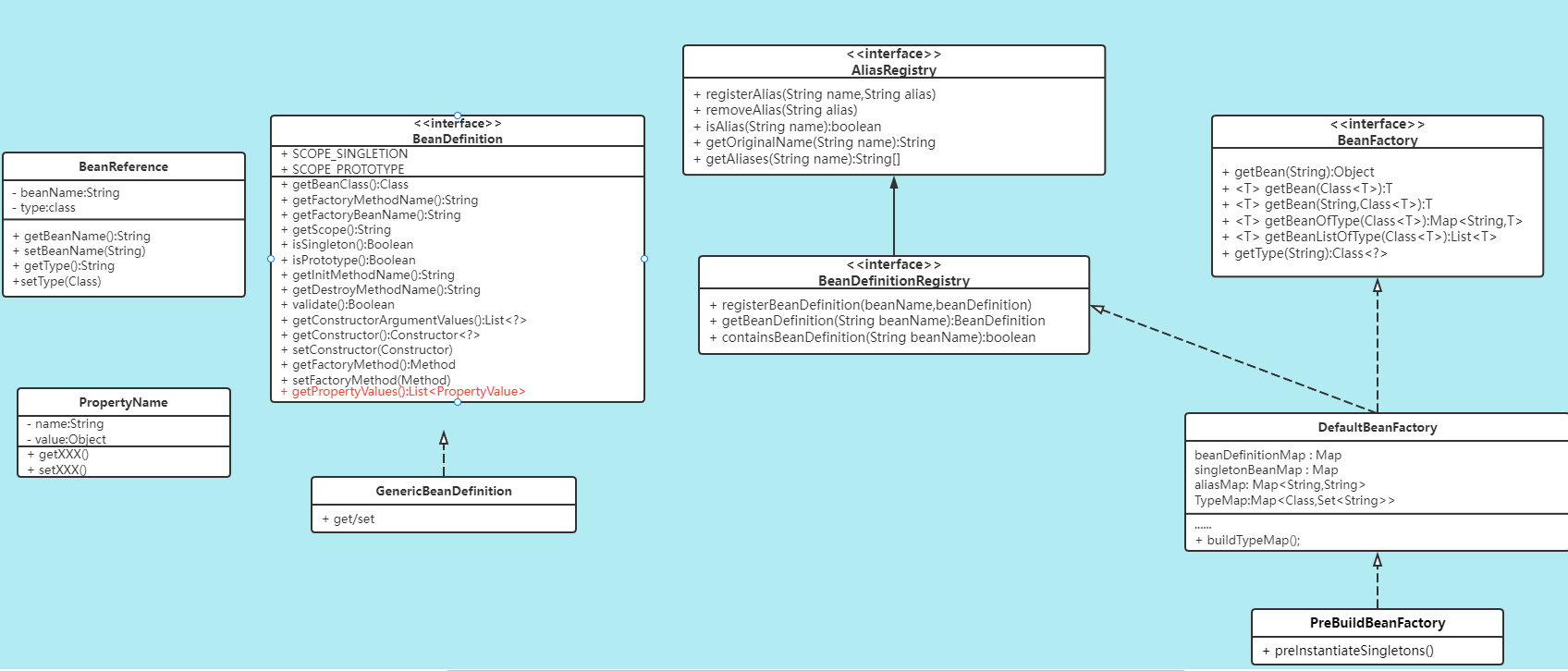
Spring源码之手写DI
Spring源码之手写DI 我们来回顾一下前面手写IOC的内容。 一、DI介绍 DI(Dependency injection)依赖注入。对象之间的依赖由容器在运行期决定,即容器动态的将某个依赖注入到对象之中。说直白点就是给Bean对象的成员变量赋值。 在这里我们就需要明白几个问题。 1.…...
从零入手人工智能(5)—— 决策树
1.前言 在上一篇文章《从零入手人工智能(4)—— 逻辑回归》中讲述了逻辑回归这个分类算法,今天我们的主角是决策树。决策树和逻辑回归这两种算法都属于分类算法,以下是决策树和逻辑回归的相同点: 分类任务࿱…...
)
go语言:两协程并发交替打印数字和字母(代码逐行注释)
要求: 并发两协程交替打印数字和字母。一个协程打印数字,一个协程打印字母。 输出: 12AB34CD56EF78GH910IJ1112KL1314MN1516OP1718QR1920ST2122UV2324WX2526YZ2728 思路: 两个 channel 控制两个协程进行交替打印。sync.WaitG…...
TWM论文阅读笔记
这是ICLR2023的一篇world model论文,用transformer来做世界模型的sequence prediction。文章贡献是transformer-based world model(不同于以往的如transdreamer的world model,本文的transformer-based world model在inference 的时候可以丢掉…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...
