[信号与系统]关于双线性变换
前言
本文还是前置知识
双线性变换法
双线性变换法(Bilinear Transform)是一种用于将模拟滤波器转换为数字滤波器的方法。它通过将模拟域中的s平面上的传递函数映射到数字域中的z平面上的传递函数来实现这一转换。双线性变换法保证了频率响应在转换过程中不会产生混叠,并且在设计IIR滤波器时非常常用。
双线性变换的基本原理
双线性变换通过以下关系将s平面的传递函数转换为z平面的传递函数:
s = 2 T ⋅ 1 − z − 1 1 + z − 1 s = \frac{2}{T} \cdot \frac{1 - z^{-1}}{1 + z^{-1}} s=T2⋅1+z−11−z−1
其中:
- s s s 是模拟域的复数频率变量。
- z z z 是数字域的复数频率变量。
- T T T 是采样周期。
这个公式将s平面的每一点双线性映射到z平面的一个点上,并且这种映射是保角的,即保持了角度关系。
双线性变换是一种用于将连续时间系统的频域表示(通常用拉普拉斯变换表示)转换为离散时间系统频域表示(通常用Z变换表示)的方法。这种转换特别有用,因为它允许我们将连续时间滤波器的设计(模拟滤波器)转化为离散时间滤波器的设计(数字滤波器),以便在数字信号处理(DSP)系统中实现。
作用:
双线性变换是将连续时间系统(模拟信号)的频域表示转换为离散时间系统(数字信号)频域表示的一种方法。通过这种变换,我们可以设计数字滤波器,使其频率响应与对应的模拟滤波器尽可能匹配。
转换过程
-
模拟传递函数:
首先,从模拟滤波器的设计得到其传递函数 H ( s ) H(s) H(s)。 -
应用双线性变换:
使用双线性变换公式,将 s s s 替换为 2 T ⋅ 1 − z − 1 1 + z − 1 \frac{2}{T} \cdot \frac{1 - z^{-1}}{1 + z^{-1}} T2⋅1+z−11−z−1,得到数字域的传递函数 H ( z ) H(z) H(z)。 -
化简传递函数:
将得到的 H ( z ) H(z) H(z) 化简为标准形式,通常表示为两个多项式的比值。
例子
假设我们有一个一阶低通模拟滤波器,其传递函数为:
H ( s ) = ω c s + ω c H(s) = \frac{\omega_c}{s + \omega_c} H(s)=s+ωcωc
其中, ω c \omega_c ωc 是截止角频率。
步骤1:应用双线性变换
使用双线性变换公式,将 s s s 替换为 2 T ⋅ 1 − z − 1 1 + z − 1 \frac{2}{T} \cdot \frac{1 - z^{-1}}{1 + z^{-1}} T2⋅1+z−11−z−1:
H ( z ) = ω c 2 T ⋅ 1 − z − 1 1 + z − 1 + ω c H(z) = \frac{\omega_c}{\frac{2}{T} \cdot \frac{1 - z^{-1}}{1 + z^{-1}} + \omega_c} H(z)=T2⋅1+z−11−z−1+ωcωc
步骤2:化简传递函数
进行化简:
H ( z ) = ω c ( 1 + z − 1 ) 2 T ( 1 − z − 1 ) + ω c ( 1 + z − 1 ) H(z) = \frac{\omega_c (1 + z^{-1})}{\frac{2}{T} (1 - z^{-1}) + \omega_c (1 + z^{-1})} H(z)=T2(1−z−1)+ωc(1+z−1)ωc(1+z−1)
H ( z ) = ω c ( 1 + z − 1 ) 2 T − 2 T z − 1 + ω c + ω c z − 1 H(z) = \frac{\omega_c (1 + z^{-1})}{\frac{2}{T} - \frac{2}{T} z^{-1} + \omega_c + \omega_c z^{-1}} H(z)=T2−T2z−1+ωc+ωcz−1ωc(1+z−1)
H ( z ) = ω c ( 1 + z − 1 ) ( 2 T + ω c ) + ( ω c − 2 T ) z − 1 H(z) = \frac{\omega_c (1 + z^{-1})}{\left( \frac{2}{T} + \omega_c \right) + \left( \omega_c - \frac{2}{T} \right) z^{-1}} H(z)=(T2+ωc)+(ωc−T2)z−1ωc(1+z−1)
最后将分子和分母乘以 T / 2 T/2 T/2 进行化简:
H ( z ) = ω c T 2 ( 1 + z − 1 ) 1 + ( ω c T − 2 ω c T + 2 ) z − 1 H(z) = \frac{\frac{\omega_c T}{2} (1 + z^{-1})}{1 + \left( \frac{\omega_c T - 2}{\omega_c T + 2} \right) z^{-1}} H(z)=1+(ωcT+2ωcT−2)z−12ωcT(1+z−1)
这就是数字滤波器的传递函数。
相关文章:

[信号与系统]关于双线性变换
前言 本文还是前置知识 双线性变换法 双线性变换法(Bilinear Transform)是一种用于将模拟滤波器转换为数字滤波器的方法。它通过将模拟域中的s平面上的传递函数映射到数字域中的z平面上的传递函数来实现这一转换。双线性变换法保证了频率响应在转换过…...
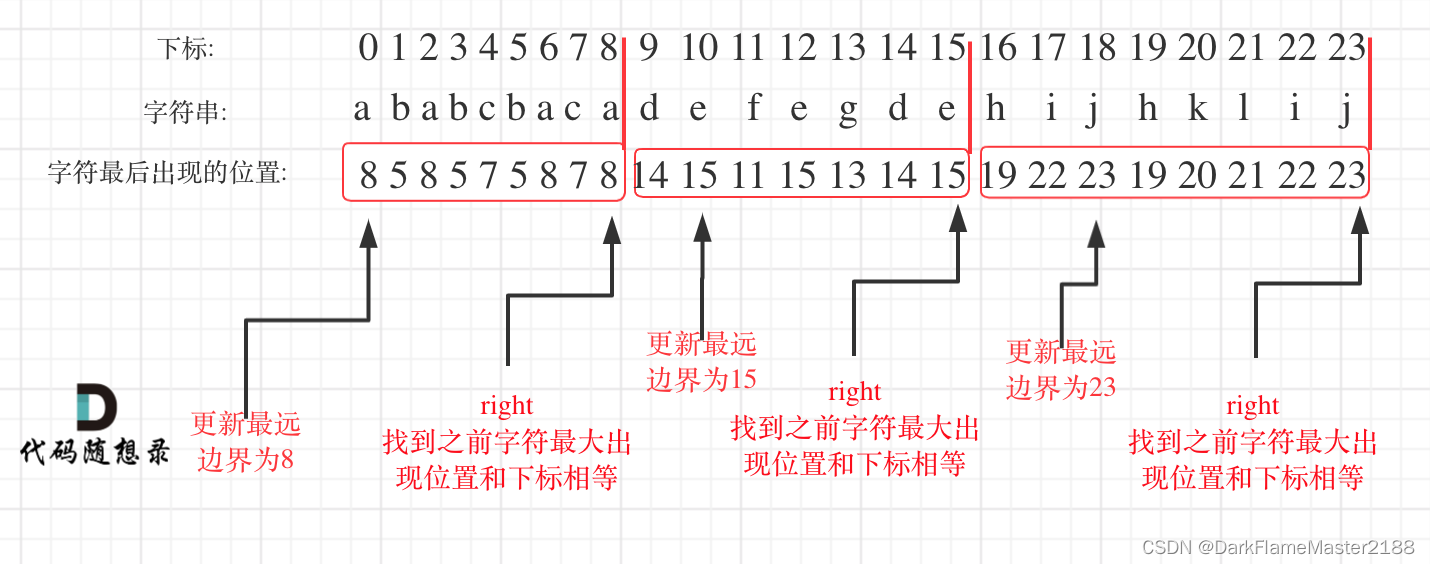
763. 划分字母区间
题目:给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。注意,划分结果需要满足:将所有划分结果按顺序连接,得到的字符串仍然是 s 。返回一个表示每个字符串片段的长度的列表…...

【PostgreSQL】AUTO_EXPLAIN - 慢速查询的日志执行计划
本文为云贝教育 刘峰 原创,请尊重知识产权,转发请注明出处,不接受任何抄袭、演绎和未经注明出处的转载。 一、介绍 在本文中,我们将了解 PostgreSQL AUTO_EXPLAIN功能的工作原理,以及为什么应该使用它来收集在生产系统…...

讯飞星火超自然语言合成的完整Demo
依赖文件和功能 requirements.txt 该文件列出了所需的依赖包。 data.py 定义了应用的配置信息,如APPId,APIKey,APISecret等。包含请求数据和请求URL。 main.py 主程序,设置了WebSocket连接,定义了处理消息的各个回调函…...
)
封装一个上拉加载的组件(无限滚动)
一、封装 1.这个是在vue3环境下的封装 2.整体思路: 2.1传入一个elRef,其实就是一个使用页面的ref。 2.2也可以不传elRef,则默认滚动的是window。 import { onMounted, onUnmounted, ref } from vue; import { throttle } from underscore;ex…...
)
WHAT - 高性能和内存安全的 Rust(二)
目录 1. 所有权(Ownership)2. 借用(Borrowing)不可变借用可变借用 3. 可变性(Mutability)4. 作用域(Scope)综合示例 了解 Rust 的所有权(ownership)、借用&am…...

办理河南建筑工程乙级设计资质的流程与要点
办理河南建筑工程乙级设计资质的流程与要点 办理河南建筑工程乙级设计资质的流程与要点主要包括以下几个方面: 流程: 工商注册与资质规划:确保企业具有独立法人资格,完成工商注册,并明确乙级设计资质的具体要求&…...

分类算法和回归算法区别
分类算法和回归算法在机器学习中扮演着不同的角色,它们的主要区别体现在输出类型、应用场景以及算法目标上。以下是对两者区别和使用场景的详细分析: 一、区别 1.输出类型: 分类算法:输出是离散的类别标签,通常表示为…...
利用Frp实现内网穿透(docker实现)
文章目录 1、WSL子系统配置2、腾讯云服务器安装frps2.1、创建配置文件2.2 、创建frps容器 3、WSL2子系统Centos服务器安装frpc服务3.1、安装docker3.2、创建配置文件3.3 、创建frpc容器 4、WSL2子系统Centos服务器安装nginx服务 环境配置:一台公网服务器(…...

怎么用Excel生成标签打印模板,自动生成二维码
环境: EXCEL2021 16.0 问题描述: 怎么用excel生成标签打印模板自动生成二维码 解决方案: 在Excel中生成标签打印模板并自动生成二维码,可以通过以下几个步骤完成: 1. 准备数据 首先,确保你的Excel表…...
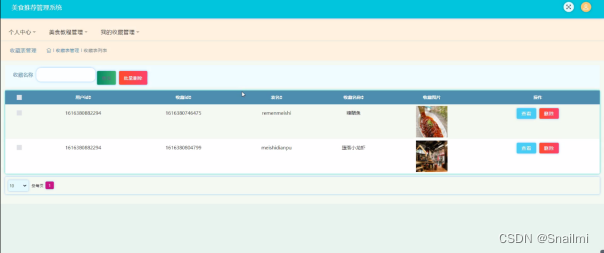
java基于ssm+jsp 美食推荐管理系统
1前台首页功能模块 美食推荐管理系统,在系统首页可以查看首页、热门美食、美食教程、美食店铺、美食社区、美食资讯、我的、跳转到后台等内容,如图1所示。 图1前台首页功能界面图 用户注册,在注册页面可以填写用户名、密码、姓名、联系电话等…...
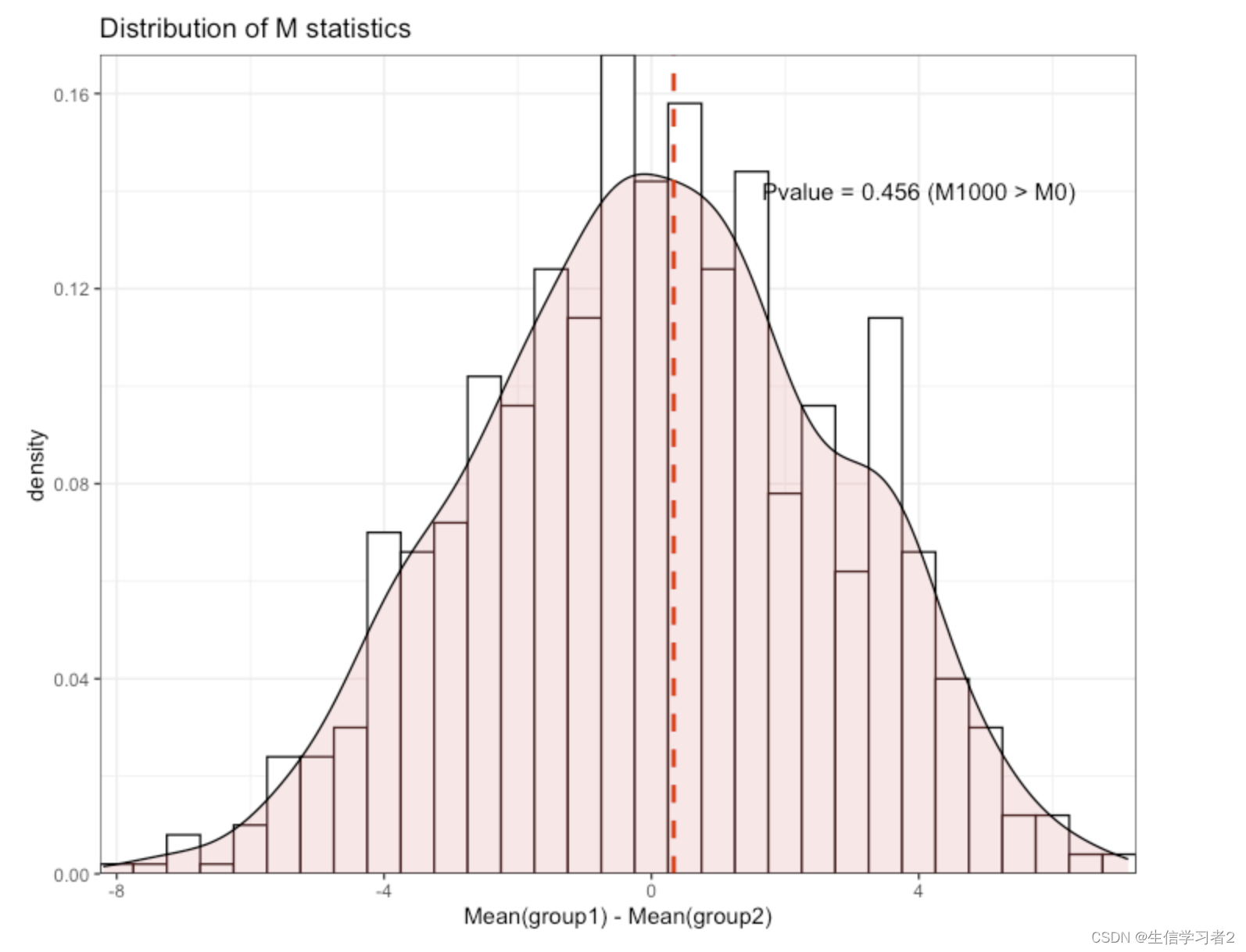
数据分析:置换检验Permutation Test
欢迎大家关注全网生信学习者系列: WX公zhong号:生信学习者Xiao hong书:生信学习者知hu:生信学习者CDSN:生信学习者2 介绍 置换检验是一种非参数统计方法,它不依赖于数据的分布形态,因此特别适…...
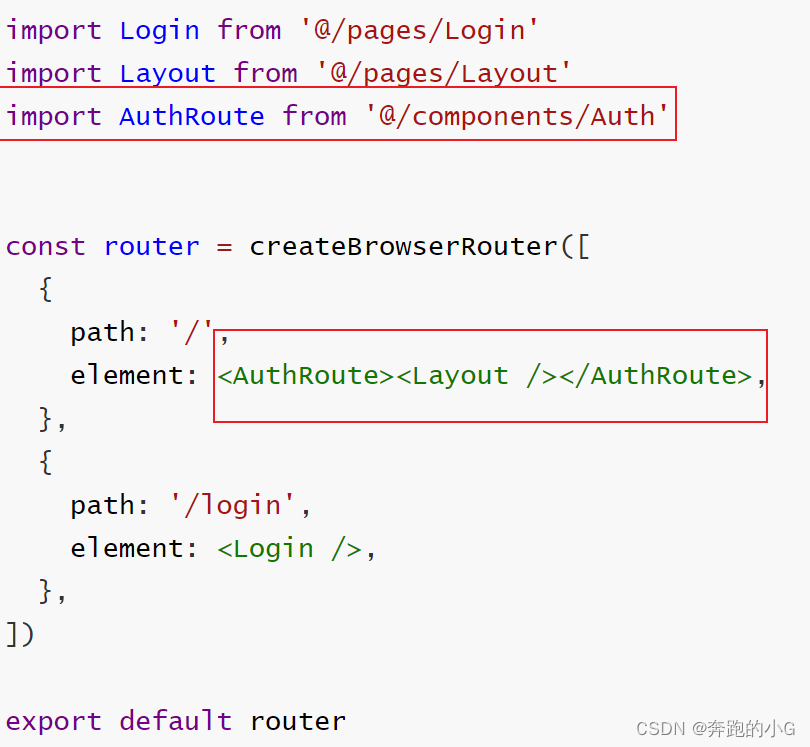
【React】使用Token做路由权限控制
在components/AuthRoute/index.js中 import { getToken } from /utils import { Navigate } from react-router-domconst AuthRoute ({ children }) > {const isToken getToken()if (isToken) {return <>{children}</>} else {return <Navigate to"/…...

机器学习周记(第四十四周:Robformer)2024.6.17~2024.6.23
目录 摘要ABSTRACT1 论文信息1.1 论文标题1.2 论文摘要1.3 论文引言1.4 论文贡献 2 论文模型2.1 问题描述2.2 Robformer2.2.1 Encoder2.2.2 Decoder 2.3 鲁棒序列分解模块2.4 季节性成分调整模块 摘要 本周阅读了一篇利用改进 Transformer 进行长时间序列预测的论文。论文模型…...

JAVA学习笔记DAY10——SpringBoot基础
文章目录 SpringBoot3 介绍SpringBoot 快速入门SpringBootApplication SpringBoot 配置文件统一配置管理Yaml 配置优势tips SpringBoot 整合 SpringMVC静态资源拦截器 interceptor SpringBoot 整合 DruidSpringBoot 整合 MybatisSpringBoot 整合 tx aopSpringBoot 打包 SpringB…...

如何在Android中实现多线程与线程池?
目录 一、Android介绍二、什么是多线程三、什么是线程池四、如何在Android中实现多线程与线程池 一、Android介绍 Android是一种基于Linux内核的开源操作系统,由Google公司领导开发。它最初于2007年发布,旨在为移动设备提供一种统一、可扩展的操作系统。…...

SCI绘图【1】-不同颜色表示密度和差异--密度图
参考资料:密度图(Density Plot) - 数据可视化图表 - 数字孪生百科 密度图是快速观察变量数值分布的有效方法之一。通常情况下,会根据两个变量将平面绘图区域分为非常多的子区域,之后以不同颜色表示落在该区域上样本的…...

C语言 while循环1
在C语言里有3种循环:while循环 do while 循环 for循环 while语句 //while语法结构 while(表达式)循环语句; 比如在屏幕上打印1-10 在while循环中 break用于永久的终止循环 在while循环中,continue的作用是跳过本次循环 …...
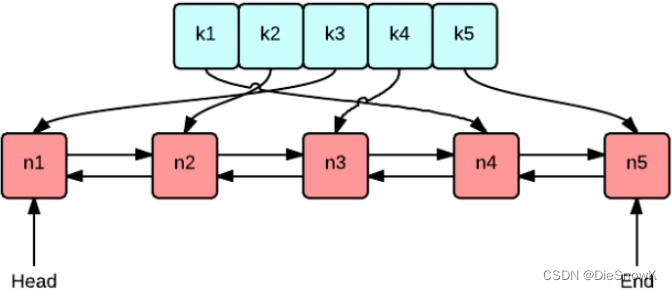
[C++][数据结构][LRU Cache]详细讲解
目录 1.什么是LRU Cache?2.LRU Cache实现 1.什么是LRU Cache? LRU是Least Recently Used的缩写,意思是最近最少使用,它是一种Cache替换算法。什么是 Cache? 狭义的Cache指的是位于CPU和主存间的快速RAM 通常它不像系统…...

怎样激励员工积极应用新版FMEA培训后的知识?
在快节奏的职场环境中,新版FMEA(失效模式与影响分析)的培训无疑是提升员工技能、优化工作流程的重要一环。然而,如何让员工积极地将所学知识应用于实际工作中,却是一个值得深入探讨的问题。下面,深圳天行健…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...
