P7771 【模板】欧拉路径
网址如下:
P7771 【模板】欧拉路径 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
忘掉了输出欧拉回路的方法,搞了我好久
关于欧拉回路的知识可以看我之前的博客:
一点关于欧拉回路的总结-CSDN博客
代码如下:
#include<queue>
#include<stack>
#include<cstdio>
#include<cmath>
using namespace std;const int maxn = 100001;struct Node{priority_queue<int, vector<int>, greater<int>> q;int indegree, outdegree;Node():indegree(0), outdegree(0){}
}node[maxn];int n;
stack<int> st;int judge(void){int cnt = 0, u = 1;for(int i = 1; i <= n; i++){if(node[i].outdegree != node[i].indegree){cnt++;if(cnt > 2 || abs(node[i].outdegree - node[i].indegree) >= 2) return -1;if(node[i].outdegree - node[i].indegree == 1) u = i;}}return u;
}
void dfs(int u){while(!node[u].q.empty()){int v = node[u].q.top();node[u].q.pop();dfs(v);}st.push(u);
}int main(void)
{int m;//输入scanf("%d%d", &n, &m);while(m--){int u, v;scanf("%d%d", &u, &v);node[u].outdegree++; node[v].indegree++;node[u].q.push(v);}//处理int u = judge();if(u == -1) printf("No");else{dfs(u);while(!st.empty()) printf("%d ",st.top()),st.pop();}return 0;
}可以看看一开始我写的错误代码(对欧拉回路理解不够深造成的):
#include<queue>
#include<cstdio>
#include<cmath>
using namespace std;const int maxn = 100001;struct Node{priority_queue<int, vector<int>, greater<int>> q;int indegree, outdegree;Node():indegree(0), outdegree(0){}
}node[maxn];int n;int judge(void){int cnt = 0, u = 1;for(int i = 1; i <= n; i++){if(node[i].outdegree != node[i].indegree){cnt++;if(cnt > 2 || abs(node[i].outdegree - node[i].indegree) >= 2) return -1;if(node[i].outdegree - node[i].indegree == 1) u = i;}}return u;
}int main(void)
{int m;//输入scanf("%d%d", &n, &m);while(m--){int u, v;scanf("%d%d", &u, &v);node[u].outdegree++; node[v].indegree++;node[u].q.push(v);}//处理int u = judge();if(u == -1) printf("No");else{printf("%d", u);while(!node[u].q.empty()){int v = node[u].q.top(); node[u].q.pop();printf(" %d", v);u = v; }}return 0;
}相关文章:

P7771 【模板】欧拉路径
网址如下: P7771 【模板】欧拉路径 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 忘掉了输出欧拉回路的方法,搞了我好久 关于欧拉回路的知识可以看我之前的博客: 一点关于欧拉回路的总结-CSDN博客 代码如下: #include<q…...
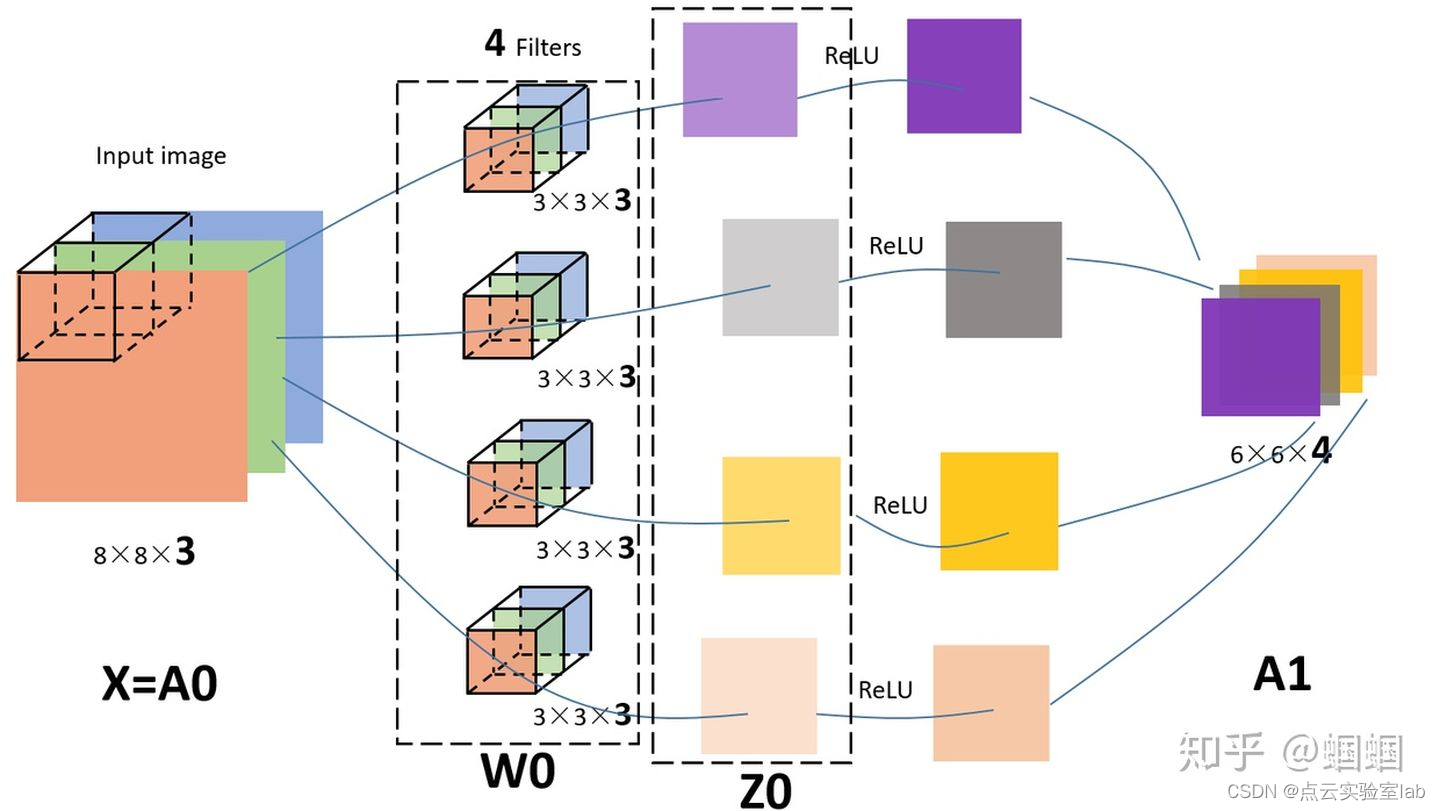
卷积神经网络(CNN)理解
1、引言(卷积概念) 在介绍CNN中卷积概念之前,先介绍一个数字图像中“边缘检测edge detection”案例,以加深对卷积的认识。图中为大小8X8的灰度图片,图片中数值表示该像素的灰度值。像素值越大,颜色越亮&…...

Databend 开源周报第 149 期
Databend 是一款现代云数仓。专为弹性和高效设计,为您的大规模分析需求保驾护航。自由且开源。即刻体验云服务:https://app.databend.cn 。 Whats On In Databend 探索 Databend 本周新进展,遇到更贴近你心意的 Databend 。 支持递归公共表…...
Hue Hadoop 图形化用户界面 BYD
软件简介 Hue 是运营和开发 Hadoop 应用的图形化用户界面。Hue 程序被整合到一个类似桌面的环境,以 web 程序的形式发布,对于单独的用户来说不需要额外的安装。...
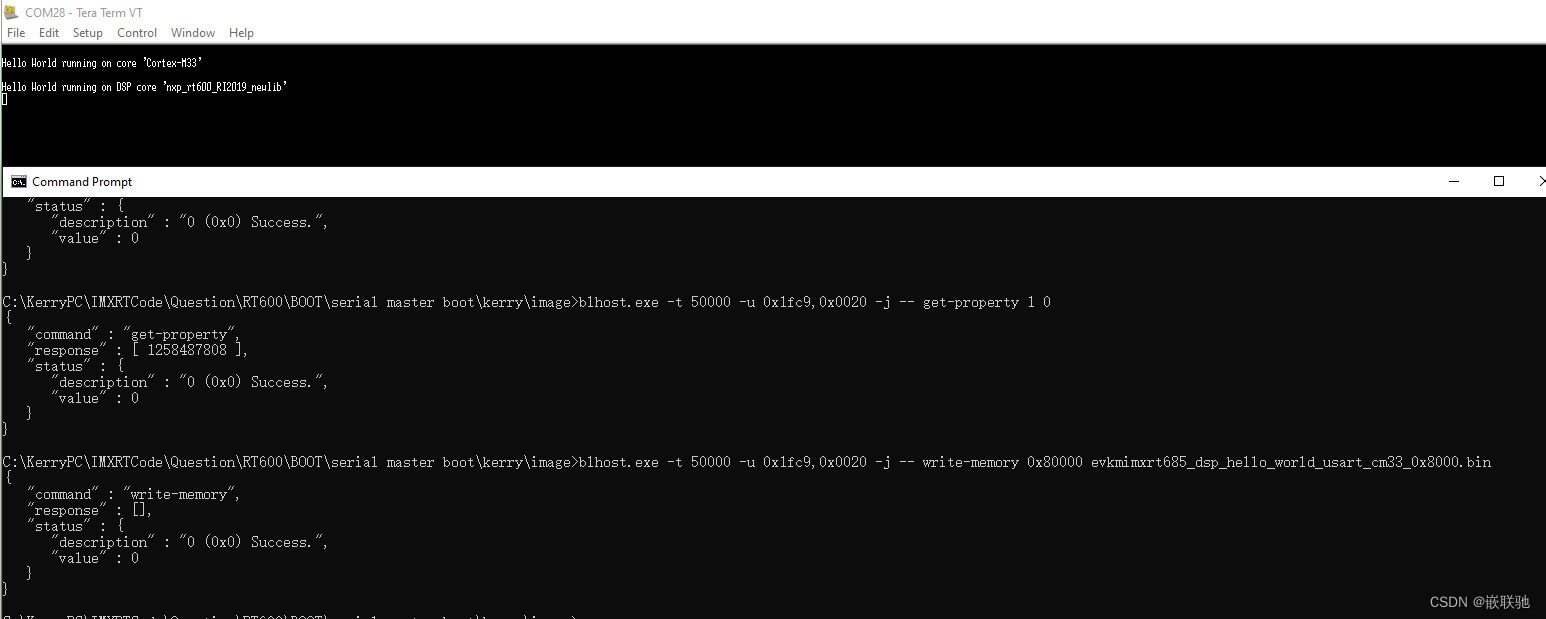
【经验分享】RT600 serial boot mode测试
【经验分享】RT600 serial boot mode测试 一, 文档描述二, Serial boot mode测试2.1 evkmimxrt685_gpio_led_output 工程测试2.2 evkmimxrt685_dsp_hello_world_usart_cm33工程测试 一, 文档描述 RT600的启动模式共支持4种: 1&am…...

七种不同类型测宽仪技术参数 看看哪种能用于您的产线?
在线测宽仪种类众多,原理不同,产品不同,型号不同,其技术参数也各不相同。不同的测量范围与测量精度,适用于不同规格的板材,看看您的板材能适用于哪种范围。 1、单测头平行光测宽仪 点光源发射的光经过发射…...

【GO】rotatelogs库和sirupsen/logrus库实现日志功能的实践用例
“github.com/sirupsen/logrus” 是一个 Go 语言的日志库,它提供了一种简单、灵活的方式来记录日志。该库的主要特点包括: 支持多种日志输出目标,如控制台、文件等。 支持日志轮转,可以按照时间或文件大小进行轮转。 支持日志格式…...

Arc2Face - 一张图生成逼真的多风格人脸,本地一键整合包下载
Arc2Face是用于人脸的基础模型训练,可批量生成超高质量主题的AI人脸艺术风格照,完美复制人脸。只需一张照片,几秒钟,即可批量生成超高质量主题的AI人脸艺术风格照,完美复制人脸。 Arc2Face 是一个创新的开源项目&…...
swiper 幻灯片
index.html <!DOCTYPE html> <html lang"en"> <head> <meta charset"utf-8"> <title>swiper全屏响应式幻灯片代码</title> <meta name"viewport" content"widthdevice-width, initial-scale1, min…...

Ubuntu 使用Vscode的一些技巧 ROS
Ubuntu VSCode的一些设置(ROS) 导入工作空间 推荐只导入工作空间下的src目录 如果将整个工作空间导入VSCode,那么这个src就变成了次级目录,容易在写程序的时候把本应该添加到具体工程src目录里的代码文件给误添加到这个catkin_w…...

JS中的三种事件模型
JavaScript 中的事件模型主要有三种: 传统事件模型(DOM Level 0)标准事件模型(DOM Level 2)IE 事件模型(非标准,仅限于旧版本的 Internet Explorer) 下面分别介绍这三种事件模型&…...

南京邮电大学计算机网络实验二(网络路由器配置RIP协议)
文章目录 一、 实验目的和要求二、 实验环境(实验设备)三、 实验步骤四、实验小结(包括问题和解决方法、心得体会、意见与建议等)五、报告资源 一、 实验目的和要求 掌握思科路由器的运行过程,掌握思科路由器的硬件连线与接口,掌…...

仓颉语言的编译和构建
一、cjc 使用 cjc是仓颉编程语言的编译命令,其提供了丰富的功能及对应的编译选项,本章将对基本使用方法进行介绍。 cjc-frontend (仓颉前端编译器)会随 cjc 一起通过 Cangjie SDK 提供,cjc-frontend 能够将仓颉源码编…...

网络基础-协议
一、ARP 通过IP得到Mac 首先会查看缓存的arp表中是否有相应的IP和Mac对应关系,如果有直接进行包封装。如果没有则进行广播当对应的地址就收到广播包后会根据arp中的源地址进行单播返回相应的IP和Mac对应关系。 arp -a 查看现有的arp缓存 二、RARP反向地址解析 通过…...
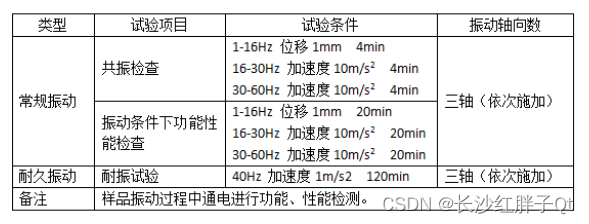
电子设备抗震等级与电子设备震动实验
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/139923445 红胖子(红模仿)的博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV、OpenGL、ffmpeg、OSG、单片机、软…...
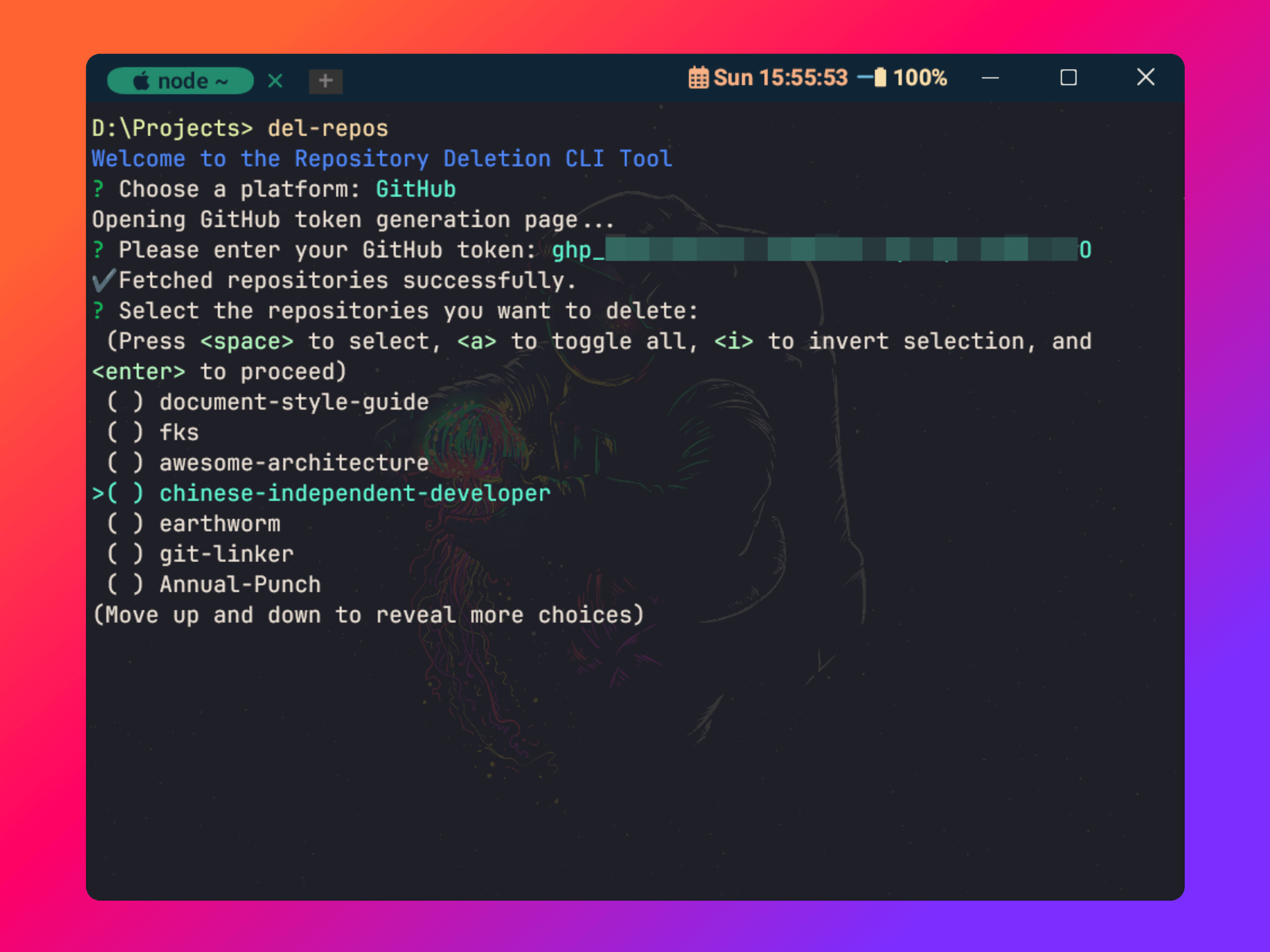
你还在手动操作仓库?这款 CLI 工具让你效率飙升300%!
前言 作为一名开发者,我经常会在 GitHub 和 Gitee 上 fork 各种项目。时间一长,这些仓库就会堆积如山,变成了“垃圾仓库”。每次打开代码托管平台,看到那些不再需要的仓库,我的强迫症就会发作。手动一个一个删除这些仓…...

未来已来!GPT-5震撼登场,工作与生活面临新变革!
随着科技界领袖对AI系统发展之快的惊叹,新一代大语言模型GPT-5即将登场,引发了我们对工作和日常生活的新一轮思考。微软CTO Kevin Scott和阿里巴巴董事长蔡崇信等人的言论为我们描绘了一幅生动的未来图景,即AI将在我们的生活中扮演越来越重要…...

洗地机选购指南,什么品牌最值得购买?2024四大口碑品牌推荐
随着炎炎夏日的到来,家里的地板清洁会成为人们“沉重”的负担,而拥有一台能够高效又轻松完成地板深度清洁的洗地机是一件非常幸福的事儿。但是,面对市场上琳琅满目的洗地机品牌和型号,如何找到一款综合性能都不错的洗地机成为了许…...

住宅IP与普通IP的区别
在互联网连接中,IP地址是识别每个网络节点的关键。在众多类型的IP地址中,住宅IP和普通IP是两种常见的分类。本文将深入探讨住宅IP与普通IP之间的主要区别。 一、定义与来源 住宅IP指的是由互联网服务提供商(ISP)直接分配给家庭或…...
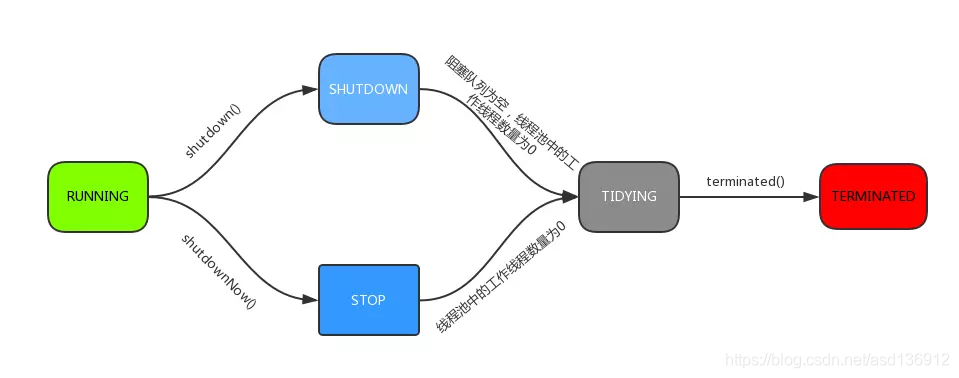
【Java】线程池技术(三)ThreadPoolExecutor 状态与运行源码解析
ThreadPoolExecutor 状态 ThreadPoolExecutor 继承了 AbstractExecutorService,并实现了 ExecutorService 接口,用于管理线程。内部使用了原子整型 AtomicInteger ctl 来表示线程池状态和 Worker 数量。前 3 位表示线程池状态,后 29 位表示 …...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...
