信息学奥赛初赛天天练-34-CSP-J2021完善程序-按位异或、模拟算法、数组模拟环、约瑟夫问题应用
PDF文档公众号回复关键字:20240624

2021 CSP-J 完善程序3
1 完善程序 (单选题 ,每小题3分,共30分)
(Josephus问题)有n个人围成一个圈,依次标号0至n-1。从0号开始,依次 0,1,0,1…交替报数,报到1的人会离开,直至只剩下一个人。求最后剩下人的编号
#include<stdio.h>const int MAXN=1000000;
int F[MAXN];int main(){int n;scanf("%d",&n);int i=0,p=0,c=0;while(①){if(F[i]==0){if(②){F[i]=1;③;}④}⑤;}int ans=-1;for(i=0;i<n;i++)if(F[i]==0)ans=i;printf("%d\n",ans);return 0;
}
34.①处应填( )
A. i<n
B. c<n
C. i<n-1
D. c<n-1
35.②处应该填( )
A. i%2==0
B. i%2==1
C. p
D. !p
36.③处应该填( )
A. i++
B. i=(i+1)%n
C. c++
D. p^=1
37.④处应该填( )
A. i++
B. i=(i+1)%n
C. c++
D. p^=1
38.⑤处应该填( )
A. i++
B. i=(i+1)%n
C. c++
D. p^=1
2 相关知识点
1) 异或运算
异或运算(XOR)是一种基本的数学运算符,应用于逻辑运算,其数学符号为“⊕”,计算机符号为“xor”
异或运算的运算法则为:如果两个值不相同,则异或结果为1;如果两个值相同,则异或结果为0
//示例
2 xor 3 = 1
具体过程如下
2 对应二进制 0010
3 对应二进制 001100100011
xor
----------0001
C++语言中 异或符号为 ^
p^=1等价p=p^1p为0时 p^1=0^1=1
具体过程如下
0对应二进制为 0000
1对应二进制为 000100000001
xor
----------0001p为1时 p^1=1^1=0
具体过程如下
1对应二进制为 000100010001
xor
----------0000
2) 约瑟夫问题
约瑟夫问题特征是有环,到最大人数后重新数,因此使用数组模拟约瑟夫问题时,达到最大需要从头开始
一轮需要有一人出去,需要一个变量标识一轮的开始结束
需要保留1人,需要一个变量统计出去的人数,进而和总人数比较
3 思路分析
34.①处应填( D )
A. i<n
B. c<n
C. i<n-1
D. c<n-1
分析
/*模拟每个人的位置,到达最大位置,重新开始p表示2人出去1人的一轮对应的值,即0 1,由于只有2次,所以当前人p为0时,下一个人p就为1c出去的人数
*/
int i=0,p=0,c=0;while(①){if(F[i]==0){if(②){F[i]=1;③;}④}⑤;}
/*由于c的初始值为0,即c为0时可以出去1人,接着c为1时继续判定可以出去1人,加上前面c为0时出去1人,总共可以出去2人c为n-2时可以出去n-1人,c为n-1时可以出去n人目标需要出去n-1人,c最大为n-2,所以判定条件为c<n-1
*/
35.②处应该填( C )
A. i%2==0
B. i%2==1
C. p
D. !p
分析
/*模拟每个人的位置,到达最大位置,重新开始p表示2人出去1人的一轮对应的值,即0 1,由于只有2次,所以当前人p为0时,下一个人p就为1c出去的人数
*/
int i=0,p=0,c=0;while(①){if(F[i]==0){if(②){F[i]=1;③;}④}⑤;}
/*for(i=0;i<n;i++)if(F[i]==0)ans=i;根据上面代码可知,输出ans是剩余的人的编号,判定是F[i]==0,所以出去的人是F[i]==1F[i]==0 改为 F[i]=1; 说明是F[i]=1时标记为出去此处是判定出去条件成立,由于是0 1 中,1出去,p初始为0,所以只有p为true或为1时才出去因此选C
*/
36.③处应该填( C )
A. i++
B. i=(i+1)%n
C. c++
D. p^=1
分析
/*模拟每个人的位置,到达最大位置,重新开始p表示2人出去1人的一轮对应的值,即0 1,由于只有2次,所以当前人p为0时,下一个人p就为1c出去的人数
*/
int i=0,p=0,c=0;while(①){if(F[i]==0){if(②){F[i]=1;③;}④}⑤;}
/*c为出去的人数,符号出去的条件c累加所以选C
*/
37.④处应该填( D )
A. i++
B. i=(i+1)%n
C. c++
D. p^=1
分析
/*模拟每个人的位置,到达最大位置,重新开始p表示2人出去1人的一轮对应的值,即0 1,由于只有2次,所以当前人p为0时,下一个人p就为1c出去的人数
*/
int i=0,p=0,c=0;while(①){if(F[i]==0){if(②){F[i]=1;③;}④}⑤;}
/*p变量模拟01变化值,下1个为0,再下1个为1,只要数数,就会变化:0变1,1变0p^=1 等价 p = p^1; -- 0通过p^1可以变为1,1通过p^1可以变为0所以选D
*/
38.⑤处应该填( B )
A. i++
B. i=(i+1)%n
C. c++
D. p^=1
分析
/*模拟每个人的位置,到达最大位置,重新开始p表示2人出去1人的一轮对应的值,即0 1,由于只有2次,所以当前人p为0时,下一个人p就为1c出去的人数
*/
int i=0,p=0,c=0;while(①){if(F[i]==0){if(②){F[i]=1;③;}④}⑤;}
/*通过对n取余,保证出去下标不会超过n,用数组模拟环所以选B
*/
相关文章:

信息学奥赛初赛天天练-34-CSP-J2021完善程序-按位异或、模拟算法、数组模拟环、约瑟夫问题应用
PDF文档公众号回复关键字:20240624 2021 CSP-J 完善程序3 1 完善程序 (单选题 ,每小题3分,共30分) (Josephus问题)有n个人围成一个圈,依次标号0至n-1。从0号开始,依次 0,1,0&#…...
【计算机视觉】人脸算法之图像处理基础知识(六)
图像直方图 图像直方图是描述图像中像素强度分布的一种统计图表,它是图像处理和计算机视觉领域中一个非常基础且重要的概念。图像直方图通常用于分析图像的亮度、对比度特性,以及在图像增强、阈值分割、特征提取等多种图像处理任务。 import cv2 impor…...
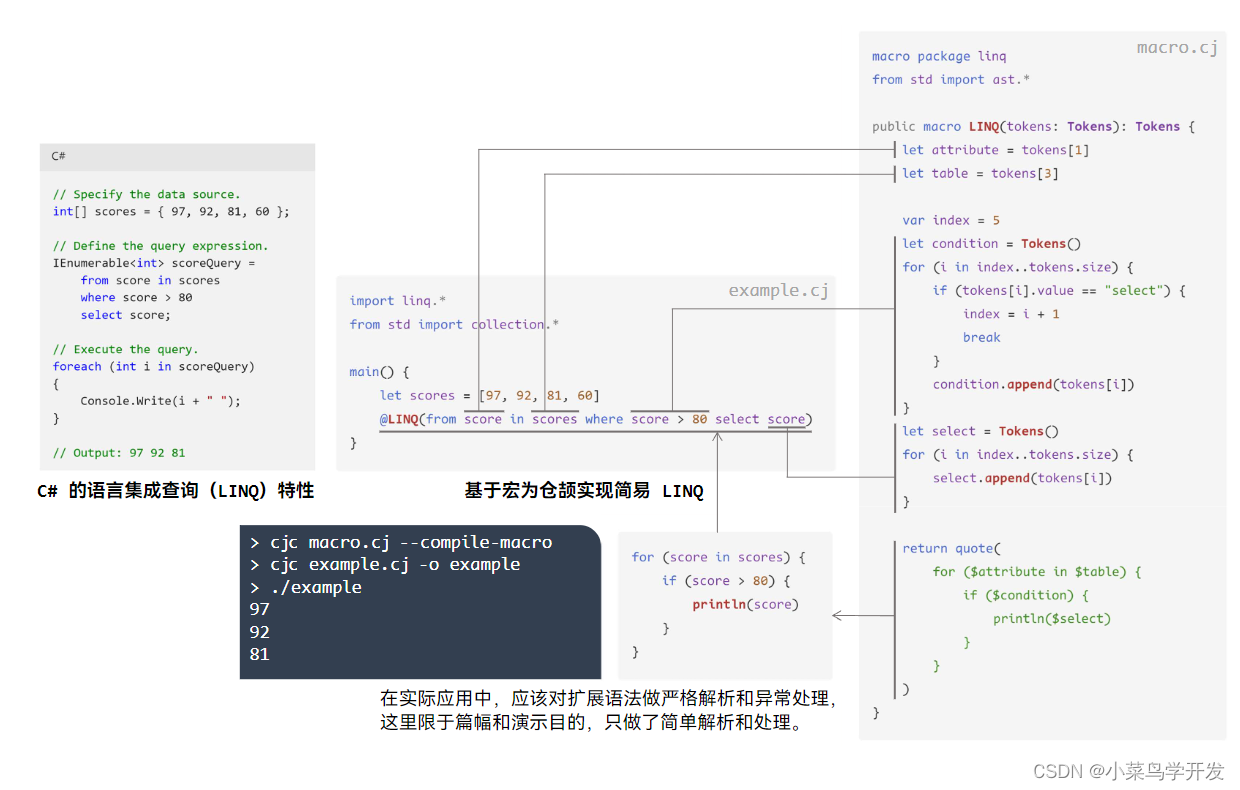
仓颉编程语言入门
华为在 2024 年 6 月 21 日的华为开发者大会上,华为终端 BG 软件部总裁龚体正式官宣了华为自研仓颉编程语言,并发布了 HarmonyOS NEXT 仓颉语言开发者预览版。 仓颉编程语言文件后缀名为 .cj, 以下是第一个入门代码输出:你好,仓颉…...

在前端项目中,如何处理错误和异常?
在前端项目中,如何处理错误和异常? 在前端项目中,处理错误和异常是至关重要的,它能确保应用程序的稳定性和用户体验。以下是一些常见的方法: try-catch-finally结构:使用JavaScript的try/catch块来捕获并…...
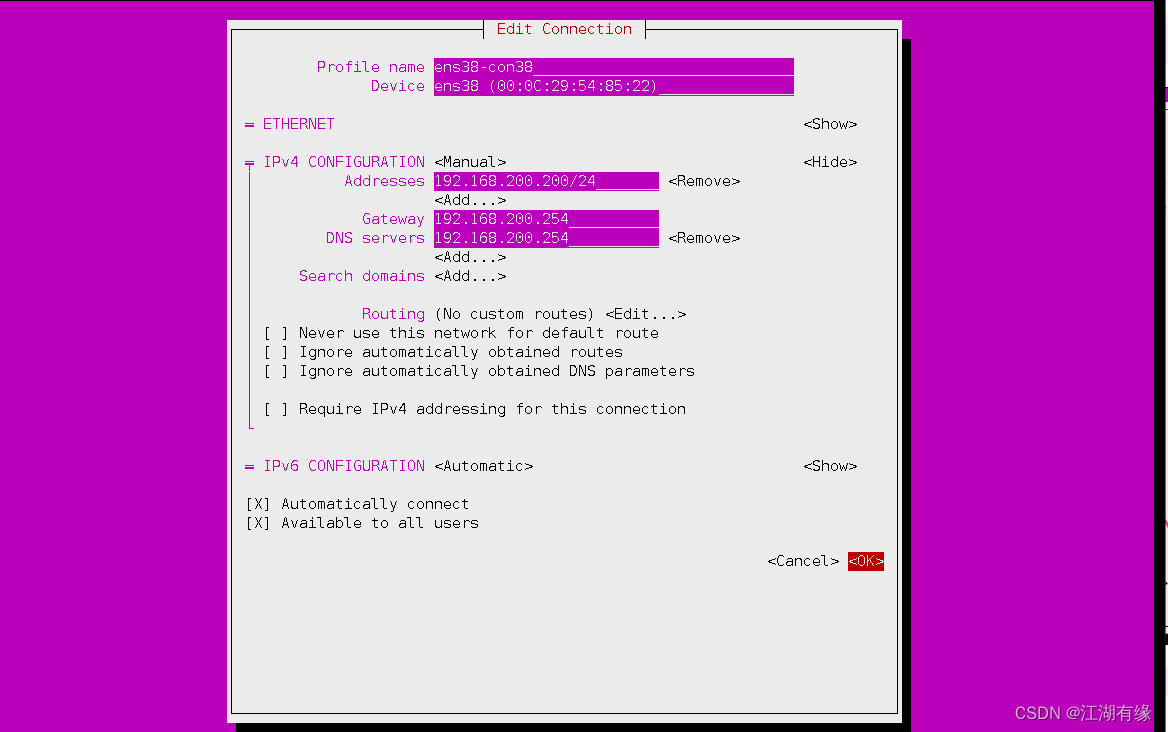
Ubuntu系统下修改网卡IP地址
Ubuntu系统下修改网卡IP地址 一、Ubuntu系统介绍1.1 Ubuntu简介1.2 Ubuntu网络配置方式 二、本地环境介绍2.1 本地环境规划2.2 本次实践介绍 三、检查本地环境3.1 检查本地操作系统版本3.2 检查系统内核版本 四、配置网卡IP地址4.1 备份网卡配置文件4.2 查看当前IP地址4.3 修改…...

Scrapy如何对爬虫数据进行清洗和处理?
爬虫数据处理是数据采集应用中至关重要的一步。scrapy是一种流行的python爬虫框架,可以帮助我们快速高效地从网页中提取所需信息。但是,我们经常面临的一个问题是数据的质量低劣,存在各种噪声和错误,这使得它们难以用于后续分析和…...
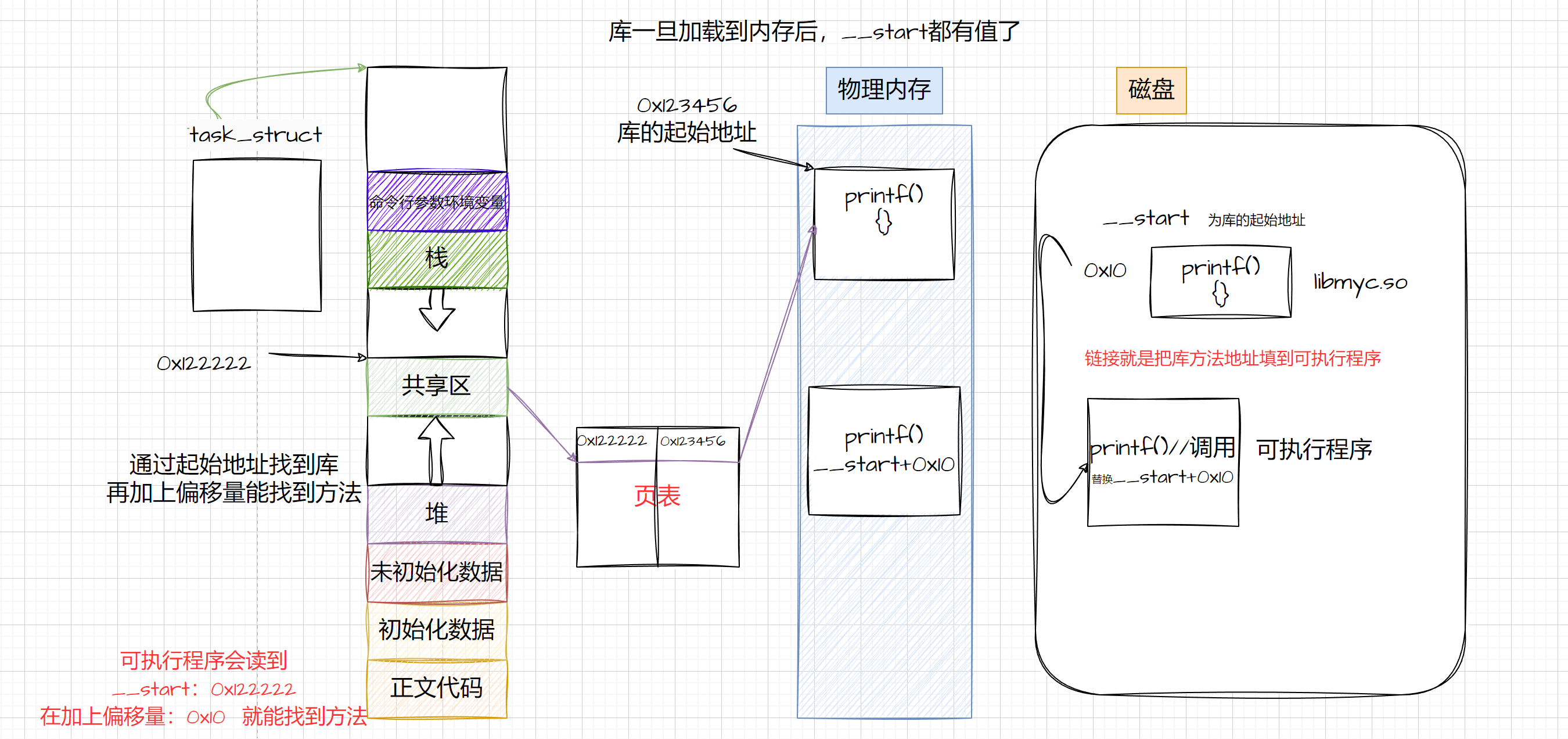
Linux:基础IO(三.软硬链接、动态库和静态库、动精态库的制作和加载)
上次介绍了基础IO(二):Linux:基础IO(二.缓冲区、模拟一下缓冲区、详细讲解文件系统) 文章目录 1.软硬链接1.1硬链接1.2软链接使用场景 2.动态库和静态库1.1回顾1.2静态库的制作和使用为什么要有库制作者角度…...
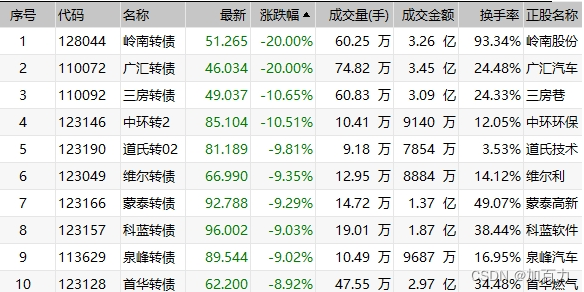
低价可转债崩盘,发生了什么?
下跌不在于“出库”,甚至不在于“风险”。问题更多在于交易层面,何时能积聚更多的左侧资金并成功过渡至右侧。 低价券怎么了? 如果说6月初主要是小微盘品种的退市风险,后来是一些评级下调的品种,到本周,已…...

【面试题】马上金九银十了,简历该准备起来了,面试题你准备好了吗 ?浅谈 JS 浅拷贝和深拷贝
代码展示 let obj_old {name: Tom,age: 15,favorite: {food: bread,drink: milk} } let obj_new {...obj_old} console.log(obj_old obj_new) // false console.log(obj_old.name obj_new.name) // true console.log(obj_old.favorite obj_new.favorite) // true3. Ar…...
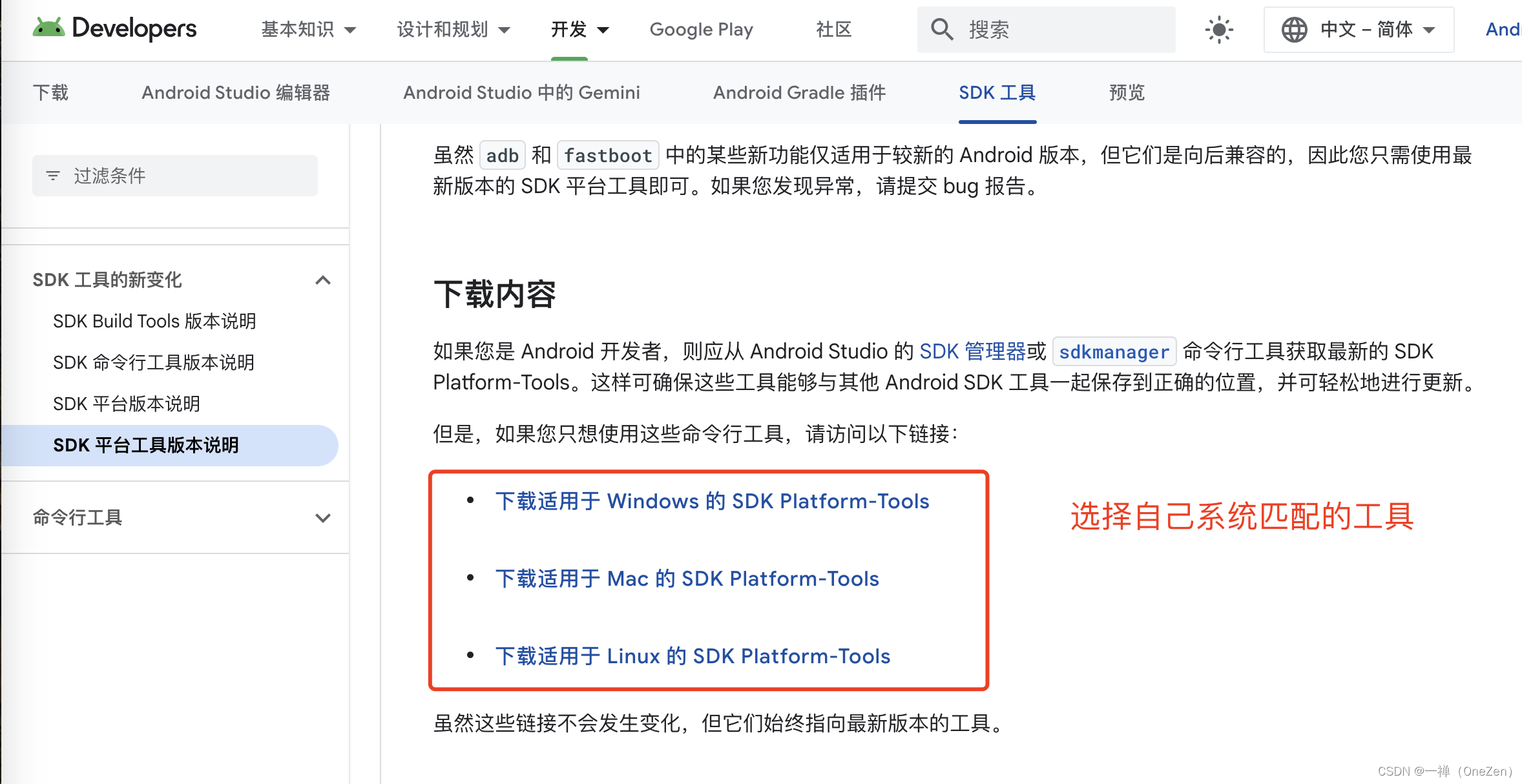
最新OPPO 真我手机 一加手机 使用adb命令永久关闭系统更新教程
使用adb命令永久关闭系统更新 一、先了解手机系统二、Android 11 以下使用adb 命令永久关闭系统更新1、adb 官方下载2、小白开启 USB 调试模式教程(熟手跳过)三、Android 12 以上使用adb 命令永久关闭系统更新什么您还是不会弄!赞赏我&#x…...

OnlyOffice:现代办公的最佳选择
目录 安装 使用 评价 对比(与WPS) 总结 在当今的数字化办公时代,选择一款功能全面且易于使用的办公软件至关重要。OnlyOffice作为一款现代化的办公软件,凭借其强大的功能和友好的用户体验,逐渐成为了众多企业和个…...
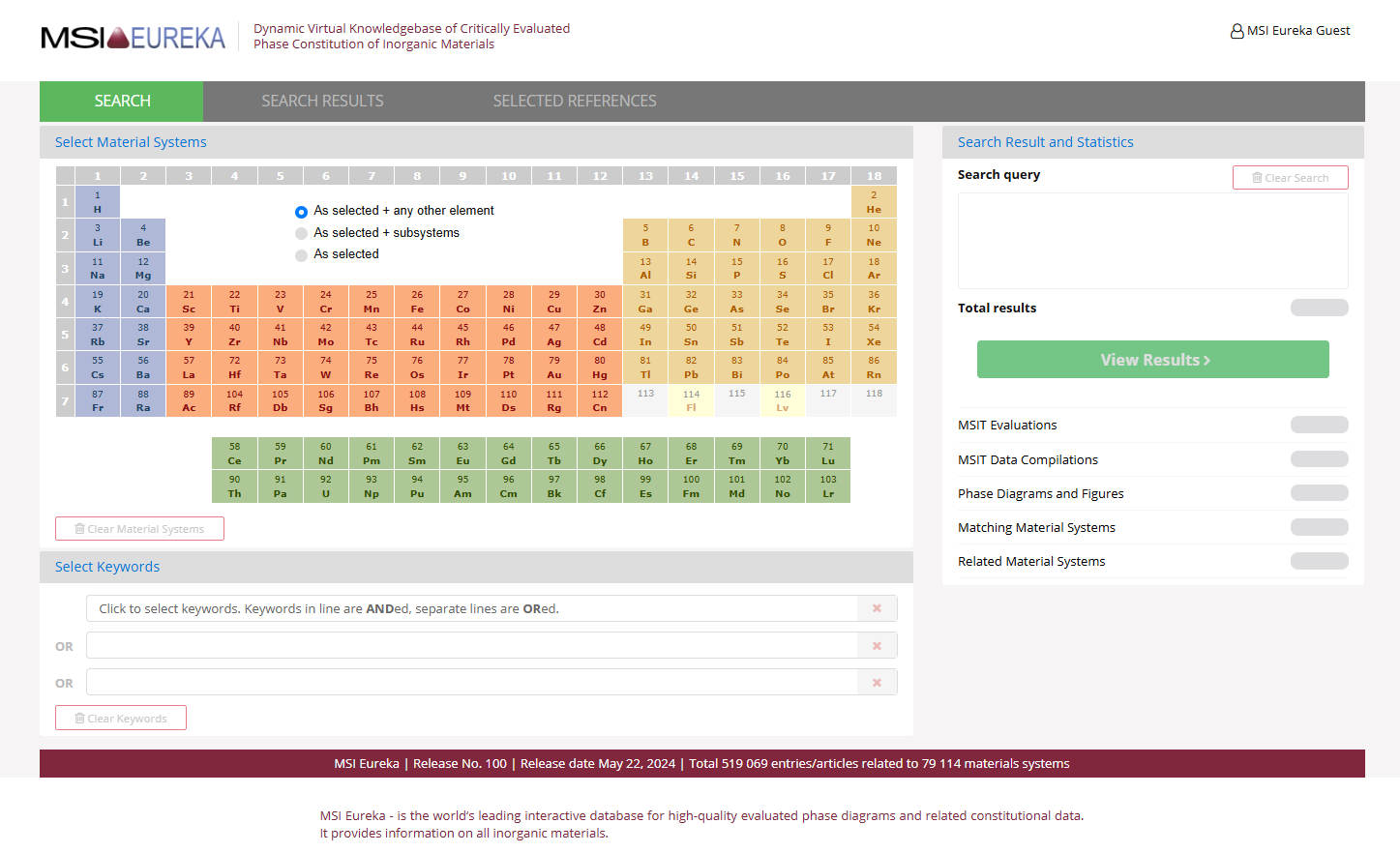
【收藏】2024年必备相图数据库资源集锦!
在材料化工领域,相图不仅仅是一个简单的图表,它是一个强大的工具,为材料科学家和工程师提供了深入理解材料行为的窗口。从选择合金元素及其比例的初步阶段,到后续的加工方法选择和热处理工艺的确定,相图都扮演着至关重…...

Zookeeper 二、Zookeeper环境搭建
Zookeeper安装方式有三种,单机模式和集群模式以及伪集群模式 单机模式:Zookeeper只运行在一台服务器上,适合测试环境集群模式:Zookeeper运行于一个集群上,适合生产环境,这个计算机集群被称为一个“集合体”…...
Web3 学习
之前学习 web3,走了不少弯路,最近看到了 hackquest,重新刷了一遍以太坊基础,感觉非常nice,而且完全免费,有需要的可以试试,链接hackquest.io。...

Grafana+Prometheus(InfluxDB)+Jmeter使用Nginx代理搭建可视化性能测试监控平台
前言 在这篇博客文章中,将分享JMeter > Prometheus(InfluxDB) > Grafana的集成,以及Nginx端口反向代理各服务的端口。 背景 在JMeter插件库中,有一些后端监听器可供Kafka、ElasticSearch和Azure使用。默认情况下,JMeter支…...
项目总结)
web学习笔记(六十六)项目总结
目录 1. Suspense标签 2.发布订阅者模式 3.pinia的使用 4.在请求过来的数据添数据 5.设置token和取token 6. 实现触底加载 7.导航守卫判断登录状态。 1. Suspense标签 Suspense主要用于用于处理异步组件加载和数据获取。,使用这个标签可以允许你在组件等待数…...
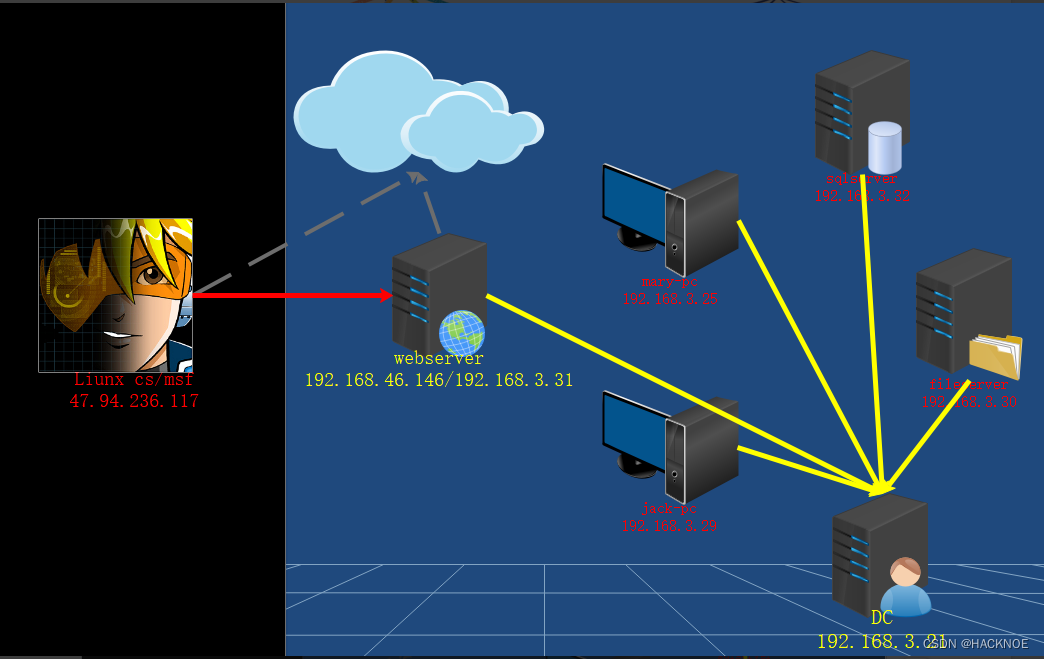
红队内网攻防渗透:内网渗透之内网对抗:横向移动篇域控系统提权NetLogonADCSPACKDC永恒之蓝CVE漏洞
红队内网攻防渗透 1. 内网横向移动1.1 横向移动-域控提权-CVE-2020-1472 NetLogon1.2 横向移动-域控提权-CVE-2021-422871.3 横向移动-域控提权-CVE-2022-269231.4 横向移动-系统漏洞-CVE-2017-01461.5 横向移动-域控提权-CVE-2014-63241. 内网横向移动 1、横向移动-域控提权-…...

VMware Workstation安装Windows Server2019系统详细操作步骤
虚拟机版本 VMware Workstation 16 Prp 16.2.5 build-20904516 实现操作 创建虚拟机 创建新的虚拟机 自定义->下一步 默认即可,下一步 稍后安装操作系统->下一步 按照图下所示选择好系统->下一步 设置好虚拟机名称和位置->下一步 默认即可࿰…...
HTML5【新特性总结】
HTML5【新特性总结】 HTML5 的新增特性主要是针对于以前的不足,增加了一些新的标签、新的表单和新的表单属性等。 这些新特性都有兼容性问题,基本是 IE9 以上版本的浏览器才支持,如果不考虑兼容性问题,可以大量使用这些新特性。…...

【面试题】面试官:判断图是否有环?_数据结构复试问题 有向图是否有环
type: NODE;name: string;[x: string]: any; }; [x: string]: any;}; export type Data Node | Edge; 复制代码 * 测试数据如下const data: Data[] [ { id: ‘1’, data: { type: ‘NODE’, name: ‘节点1’ } }, { id: ‘2’, data: { type: ‘NODE’, name: ‘节点2’ } },…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...
