C/C++每日一练(20230311)

目录
1. 计算阶乘的和 ★
2. 基本计算器 ★★★
3. N皇后 II ★★★
🌟 每日一练刷题专栏
C/C++ 每日一练 专栏
Python 每日一练 专栏
1. 计算阶乘的和
计算:1!-2!+3!-4!+5!-6!+7!-8!+9!-10!,并输出计算结果。
注意:不全是加法,而是 ∑ n! * (-1)^(n-1),加减混合的“代数和”。
代码:
#include "stdio.h"
double fun(int n)
{double sum=1.0;int i;for(i=1;i<=n;i++)sum*=i;return sum;
}int main()
{int i,mark=1;double sum=0,item=0;for(i=1;i<=10;i++){item=mark*fun(i);sum+=item;mark=-mark;}printf("1!-2!+3!-4!+5!-6!+7!-8!+9!-10! = %.0lf\n",sum);return 0;
}输出:
1!-2!+3!-4!+5!-6!+7!-8!+9!-10! = -3301819
也可以不用像上面原题附带的代码一样自定义阶乘函数,其实只用一个循环就能搞定,非常简洁:
#include "stdio.h"
int main()
{
long sum=0, fac=-1;
for(int i=1;i<=10;i++)
{
fac *= -i;
sum += fac;
}
printf("1!-2!+3!-4!+5!-6!+7!-8!+9!-10! = %ld\n", sum);
return 0;
}
2. 基本计算器
给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。
示例 1:
输入:s = "1 + 1" 输出:2
示例 2:
输入:s = " 2-1 + 2 " 输出:3
示例 3:
输入:s = "(1+(4+5+2)-3)+(6+8)" 输出:23
提示:
1 <= s.length <= 3 * 10^5s由数字、'+'、'-'、'('、')'、和' '组成s表示一个有效的表达式
代码:
#include <bits/stdc++.h>
using namespace std;class Solution
{
public:int calculate(string s){stack<int> myStack;stack<char> myOperator;int i;for (i = 0; i < s.length(); i++){while (i < s.length() && s[i] == ' ')i++;if (i == s.length())break;if (s[i] == '+' || s[i] == '-' || s[i] == '(')myOperator.push(s[i]);else if (s[i] == ')'){while (myOperator.top() != '('){int element1 = myStack.top();myStack.pop();int element2 = myStack.top();myStack.pop();char op = myOperator.top();myOperator.pop();if (op == '+')myStack.push(element1 + element2);else if (op == '-')myStack.push(element2 - element1);}if (!myOperator.empty())myOperator.pop();while (!myOperator.empty() && (myOperator.top() != '(')){int element1 = myStack.top();myStack.pop();int element2 = myStack.top();myStack.pop();char op = myOperator.top();myOperator.pop();if (op == '+')myStack.push(element1 + element2);else if (op == '-')myStack.push(element2 - element1);}}else{long long int number = 0;int j = i;while (j < s.length() && (s[j] - '0' <= 9) && (s[j] - '0' >= 0)){number = number * 10 + (s[j] - '0');j++;}i = j - 1;myStack.push(number);while (!myOperator.empty() && (myOperator.top() != '(')){int element1 = myStack.top();myStack.pop();int element2 = myStack.top();myStack.pop();char op = myOperator.top();myOperator.pop();if (op == '+')myStack.push(element1 + element2);else if (op == '-')myStack.push(element2 - element1);}}}return myStack.top();}
};int main()
{Solution sol;string s = "1 + 1";cout << sol.calculate(s) << endl;s = "2-1 + 2";cout << sol.calculate(s) << endl;s = "(1+(4+5+2)-3)+(6+8)";cout << sol.calculate(s) << endl;return 0;
}输出:
2
3
23
3. N皇后 II
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回 n 皇后问题 不同的解决方案的数量。
示例 1:
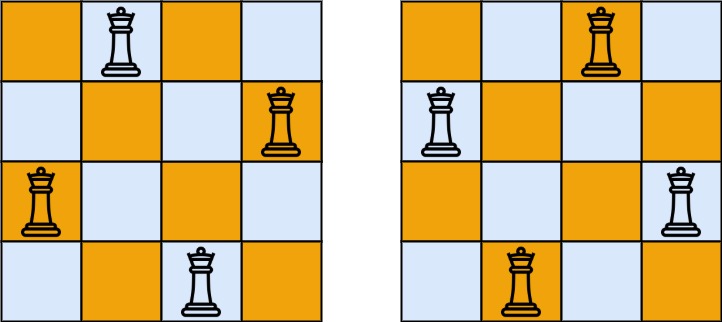
输入:n = 4 输出:2 解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1 输出:1
提示:
1 <= n <= 9- 皇后彼此不能相互攻击,也就是说:任何两个皇后都不能处于同一条横行、纵行或斜线上。
代码:
#include <bits/stdc++.h>
using namespace std;class Solution
{
public:int totalNQueens(int n){vector<int> stack(n);return dfs(n, 0, stack);}
private:int dfs(int n, int row, vector<int> &stack){int count = 0;if (row == n){return count + 1;}else{for (int i = 0; i < n; i++){if (row == 0 || !conflict(stack, row, i)){stack[row] = i;count += dfs(n, row + 1, stack);}}return count;}}bool conflict(vector<int> &stack, int row, int col){for (int i = 0; i < row; i++){if (col == stack[i] || abs(row - i) == abs(col - stack[i])){return true;}}return false;}
};int main()
{Solution sol;cout << sol.totalNQueens(4) << endl;cout << sol.totalNQueens(1) << endl;return 0;
}输出:
2
1
附录
贪心算法
又称贪婪算法, greedy algorithm
是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,算法得到的是在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择。
一般步骤
①建立数学模型来描述问题 。
②把求解的问题分成若干个子问题 。
③对每个子问题求解,得到子问题的局部最优解 。
④把子问题的解局部最优解合成原来解问题的一个解 。
贪心算法是一种对某些求最优解问题的更简单、更迅速的设计技术。贪心算法的特点是一步一步地进行,常以当前情况为基础根据某个优化测度作最优选择,而不考虑各种可能的整体情况,省去了为找最优解要穷尽所有可能而必须耗费的大量时间。贪心算法采用自顶向下,以迭代的方法做出相继的贪心选择,每做一次贪心选择,就将所求问题简化为一个规模更小的子问题,通过每一步贪心选择,可得到问题的一个最优解。虽然每一步上都要保证能获得局部最优解,但由此产生的全局解有时不一定是最优的,所以贪心算法不要回溯 。
使用条件
利用贪心法求解的问题应具备如下2个特征:
1、贪心选择性质
一个问题的整体最优解可通过一系列局部的最优解的选择达到,并且每次的选择可以依赖以前作出的选择,但不依赖于后面要作出的选择。这就是贪心选择性质。对于一个具体问题,要确定它是否具有贪心选择性质,必须证明每一步所作的贪心选择最终导致问题的整体最优解。
2、最优子结构性质
当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。问题的最优子结构性质是该问题可用贪心法求解的关键所在。在实际应用中,至于什么问题具有什么样的贪心选择性质是不确定的,需要具体问题具体分析。
存在问题
贪心算法也存在如下问题:
1、不能保证解是最佳的。因为贪心算法总是从局部出发,并没从整体考虑 ;
2、贪心算法一般用来解决求最大或最小解 ;
3、贪心算法只能确定某些问题的可行性范围 。
应用实例
例如,平时购物找零钱时,为使找回的零钱的硬币数最少,不要求找零钱的所有方案,而是从最大面值的币种开始,按递减的顺序考虑各面额,先尽量用大面值的面额,当不足大面值时才去考虑下一个较小面值,这就是贪心算法。
有很多经典的应用,比如霍夫曼编码,普利姆和克鲁斯卡尔最小生成树算法,还有迪杰斯特拉单源最短路径算法,都是使用了这种思维。
(附录部分摘自百度百科)
🌟 每日一练刷题专栏
✨ 持续,努力奋斗做强刷题搬运工!
👍 点赞,你的认可是我坚持的动力!
★ 收藏,你的青睐是我努力的方向!
✏️ 评论,你的意见是我进步的财富!
 | C/C++ 每日一练 专栏 |
 | Python 每日一练 专栏 |
相关文章:

C/C++每日一练(20230311)
目录 1. 计算阶乘的和 ★ 2. 基本计算器 ★★★ 3. N皇后 II ★★★ 🌟 每日一练刷题专栏 C/C 每日一练 专栏 Python 每日一练 专栏 1. 计算阶乘的和 计算:1!-2!3!-4!5!-6!7!-8!9!-10!,并输出计算结果。 注意:不全是…...

哪个牌子的洗地机耐用?耐用的洗地机推荐
作为当下非常热销的洗地机,它不仅解放了双手,使用也非常的便捷。是生活品质提高的最好代表,但是面对市面上让人眼花缭乱的洗地机,挑选几个来回都决定不了到底入手哪个好!为了能帮助大家选购到合适的洗地机,…...

搭建一个中心化的定时服务
1. 背景 在物联网络,很多设备之间都在进行交互,其中云端在远程交流中起到了很重要的作用。比如,一台设备想进行调温,但是需要知道此时房间的温度,那就需要定时去查询传感器测出来的房间温度,如果温度过高&a…...
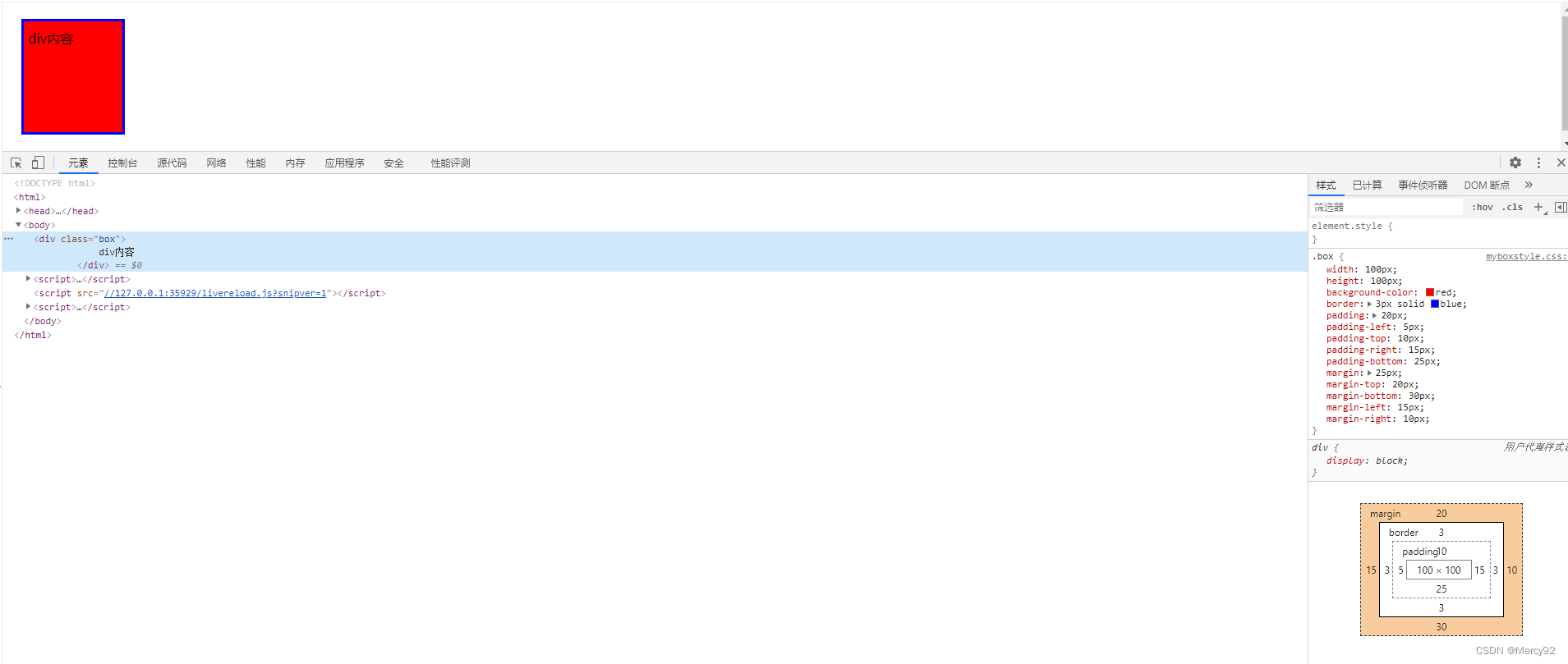
【CSS】快速入门笔记
视频链接:https://www.bilibili.com/video/BV1mS4y1Z7Ga/?spm_id_from333.999.0.0&vd_source1ad00d913eae8281cbadad6ae66fb06c 文章目录一、CSS语法1.结构2.样式类型1)内联样式 Inline Style2)内部样式 Internal Style3)外部…...
第161篇 笔记-去中心化的含义
本文主要内容来自Vitalik Buterin的文章。“去中心化”这个词是在加密经济学领域用得最多的一个词,通常也作为辨别区块链的依据。然而,这个词也可能是被定义得最不恰当的一个词。数千小时的研究和价值数十亿美元哈希算力的投入都旨在实现去中心化&#x…...

「计算机组成原理」数据的表示和运算(二)
文章目录五、奇偶校验码六、算术逻辑单元ALU6.1 电路的基本原理6.2 加法器的设计6.2.1 一位全加器6.2.2 串行加法器6.2.3 串行进位的并行加法器6.2.4 并行进位的并行加法器七、补码加减运算器八、标志位的生成九、定点数的移位运算9.1 算数移位9.2 逻辑移位9.3 循环移位五、奇偶…...
建立自己的博客
环境安装: w10系统安装 第一步:安装git Git 官网: https://git-scm.com/ 第二步:安装Node.js Node.js官网:https://nodejs.org/zh-cn/ 使用cmd检测: node -v 第三步:安装Hexo Hexo官网:htt…...
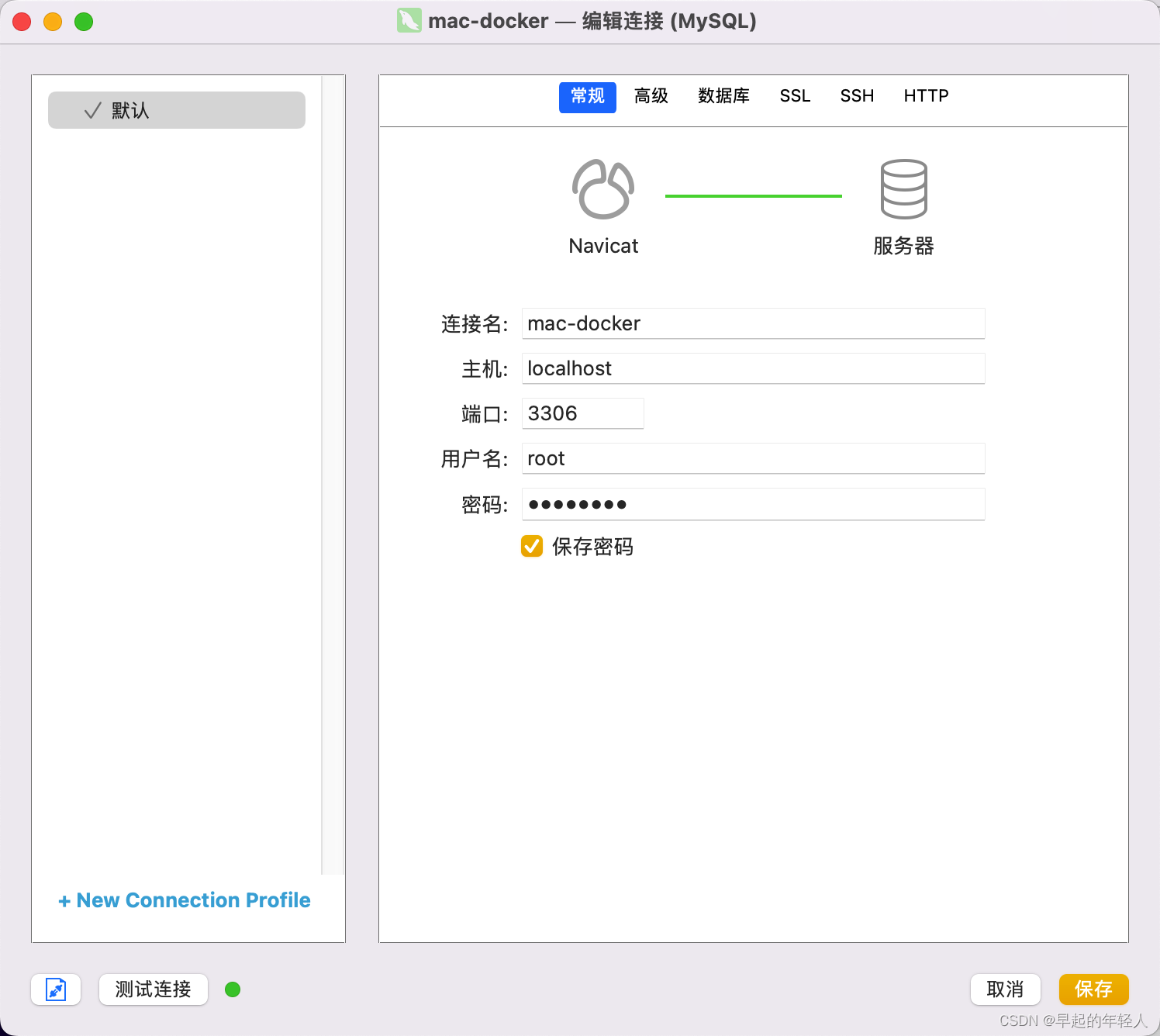
Docker 安装mysql Mac 环境下
已安装桌面端 Docker (Mac安装Docker) 安装方式一 打开链接 https://www.docker.com/products/docker-desktop 选择平台下载 安装方式二 安装homebrew /usr/bin/ruby -e "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/m…...
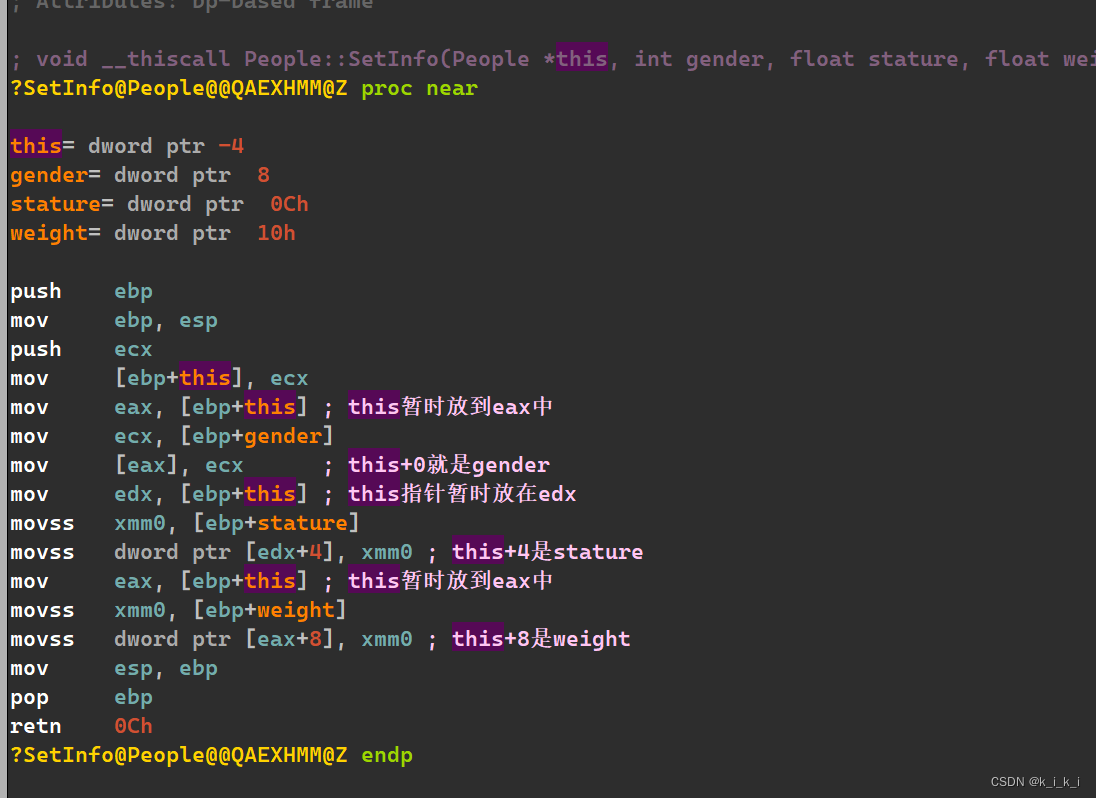
《C++代码分析》第三回:类成员函数覆盖父类函数的调用(分析this指针的变化)
一、前言 在C的学习中我们知道,子类是可以覆盖父类的方法,这里我们探讨一下子类方法调用父类方法时this指针时如何变化的。 二、示例代码 #include "windows.h" #include "windef.h" #include <iostream> #include <tch…...

Altium designer--软件简介及安装教程(Altium designer16)
一、软件介绍(完整安装包资源见文末链接,含破解license) Altium Designer 是一款简单易用、原生3D设计增强的一体化设计环境,结合了原理图、ECAD库、规则和限制条件、BoM、供应链管理、ECO流程和世界一流的PCB设计工具。通过原理…...

Windows系统下基于开源软件的多物理场仿真
Windows系统下基于开源软件的多物理场仿真实践技术应用随着计算机技术的发展,计算机仿真技术日益成为继实验和理论之后的第三种重要研究和设计手段。真实世界中遇到的问题往往是固体力学,流体力学,热,电磁等多种现象耦合而成&…...

【STL】list剖析及模拟实现
✍作者:阿润菜菜 📖专栏:C 初识list 1. list基本概况 list是可以在常数范围内在任意位置进行插入和删除的序列式容器,并且该容器可以前后双向迭代。list的底层是双向链表结构,双向链表中每个元素存储在互不相关的独立…...

Go打包附件内容到执行文件
前言 如果我们的应用在启动的时候需要对数据库进行初始化(比如建表等), 可以通过读取.sql文件内容直接执行. 但是, 这样会带出一个问题: 在发送可执行文件的时候, 需要连带着附件文件, 并且相对路径还不能出错. 这样太麻烦了有时我们并不希望附件的内容被使用者看到 处于种种…...

Spring的配置属性
介绍 以前都是用XML来设置属性值,SpringBoot的自动配置可以简化Spring应用的开发。配置属性只是配置Spring应用上下文中bean的属性而已,可以通过多个源来配置,包括JVM系统属性、环境变量等。 Spring中有两种不同(但相关)的配置 bean装配&…...

132.《render-props, Hoc,自定义hooks 详解》
文章目录render-props 模式props 方式children 方式(推荐)Hoc(高阶组件)使用步骤示例props 丢失解决方案自定义 hook1.只执行一次2.防抖hook高阶组件与自定义hook有什么区别相同点不同点React 中代码逻辑复用有三种方式,render-props, Hoc&am…...

通过Session共享数据验证码进行用户登录
通过Session共享数据验证码进行用户登录 需求: 访问带有验证码的登录页面login.jsp。用户输入用户名,密码以及验证码。 ①。如果用户名和密码输入有误,跳转登陆页面,提示:用户名或密码错误。 ②。如果验证码输入有误…...
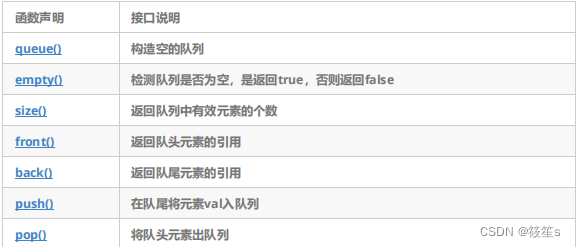
C++STL详解(六)——stack和queue
文章目录空间适配器stackstack的定义方式stack的使用stack的模拟实现queuequeue的定义方式queue的使用queue的模拟实现空间适配器 适配器是一种设计模式(设计模式是一套被反复使用的,多数人知晓的,经过分类编目的,代码设计经验的…...

javaEE 初阶 — CSS 的 基本语法 与 引入方式
文章目录1. 基本语法规范2. 三种引入方式1. 基本语法规范 CSS 的基本语法规范是由 选择器 和 若干个声明 组成的。 选择器选中一个元素之后,这些属性都是针对于这个元素展开的。 先来看一个没有 CSS 的效果。 <body><p>这是一个段落</p> </bo…...
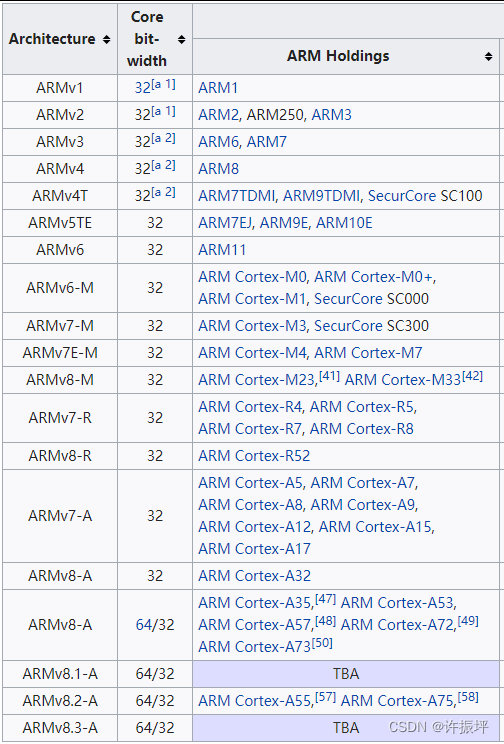
QEMU启动ARM32 Linux内核
目录前言前置知识ARM Versatile Express开发板简介ARM处理器家族简介安装qemu-system-arm安装交叉编译工具交叉编译ARM32 Linux内核交叉编译ARM32 Busybox使用busybox制作initramfs使用QEMU启动ARM32 Linux内核模拟vexpress-a9开发板模拟vexpress-a15开发板参考前言 本文介绍采…...

than的用法合集
首先需要了解一下than的词性,其有两个词性,一个是介词,一个是连词。 介词后面一定要接上名词性的词语,比如 i am taller then him 我比我的老师高 连词就比较自由,一般用来连接两个句子;但是使用than连词词…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...
