当前位置： 首页 > news >正文

浅谈Tomcat

news 2026/2/8 14:56:21

文章目录

  • 一、什么是Tomcat？
  • 二、Tomcat的下载安装
  • 三、使用tomcat访问资源

一、什么是Tomcat？

Tomcat 就是一个 HTTP 服务器。

前面我们聊了HTTP服务器，像我们在网页输入URL，其实就是在给人家的HTTP服务器发送请求，既然有HTTP服务器，那就肯定有HTTP客户端。

HTTP客户端，就是我们日常使用的浏览器。

我们自己也可以搭建一个HTTP服务器，其实就是搭建网站的 ”后端部分“，本质上就是写个 TCP socket 服务器。但是会比较麻烦，有许多重复性的工作。

因此就可以使用别人已经实现了的现成 HTTP 服务器进行网站开发，此时就不用自己从头到尾开发一个服务器了，只需要基于这些HTTP服务器进行二次开发即可。

学习了Tomcat之后，需要能够熟练运用Tomcat的api，并且基于Tomcat开发网站后端程序。

二、Tomcat的下载安装

1）、打开官网下载：官网链接
在这里插入图片描述
(上面的 Apache 是一个开源组织，开发了很多程序)
安装好tomcat后，可以将其文件夹解压缩，看看文件夹里的目录：
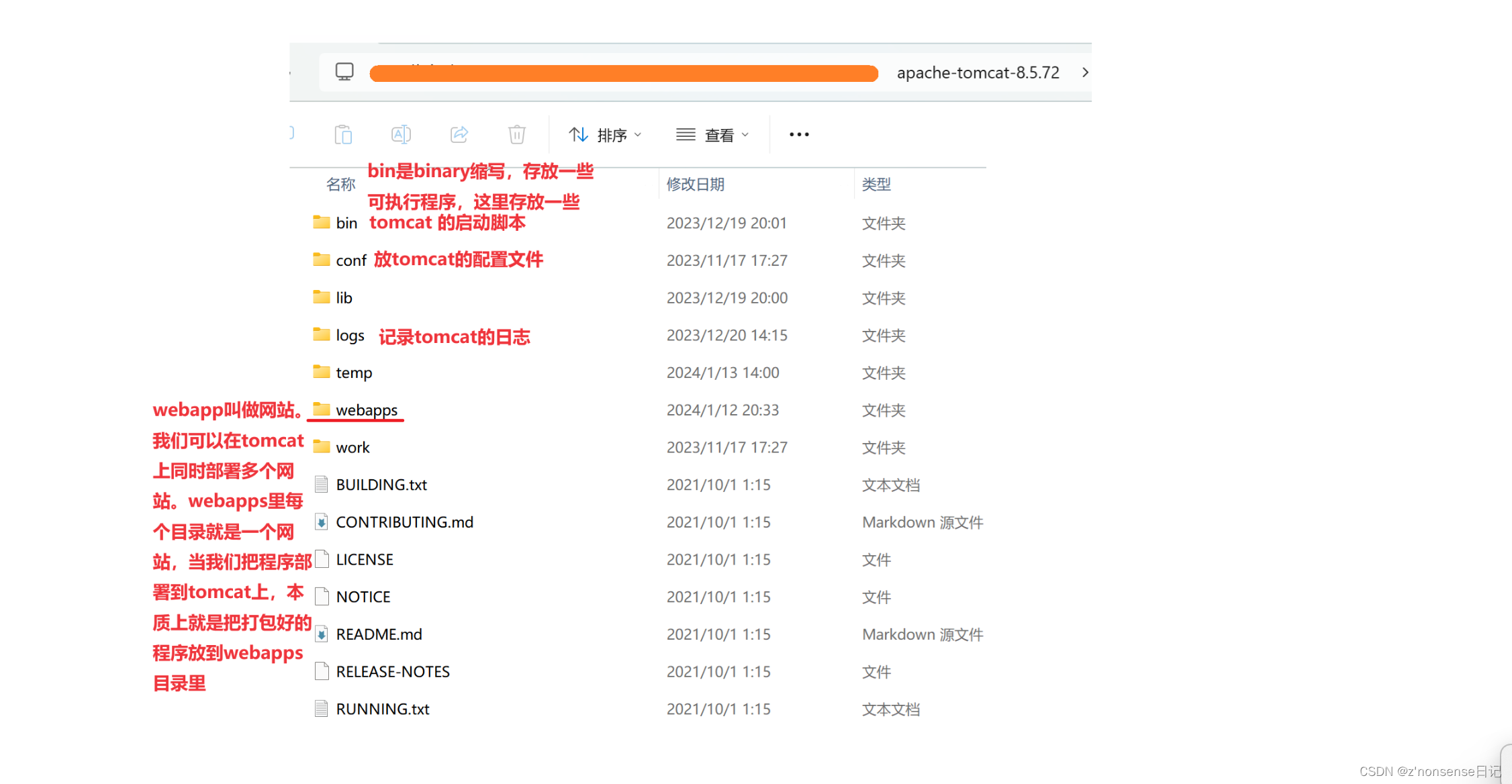
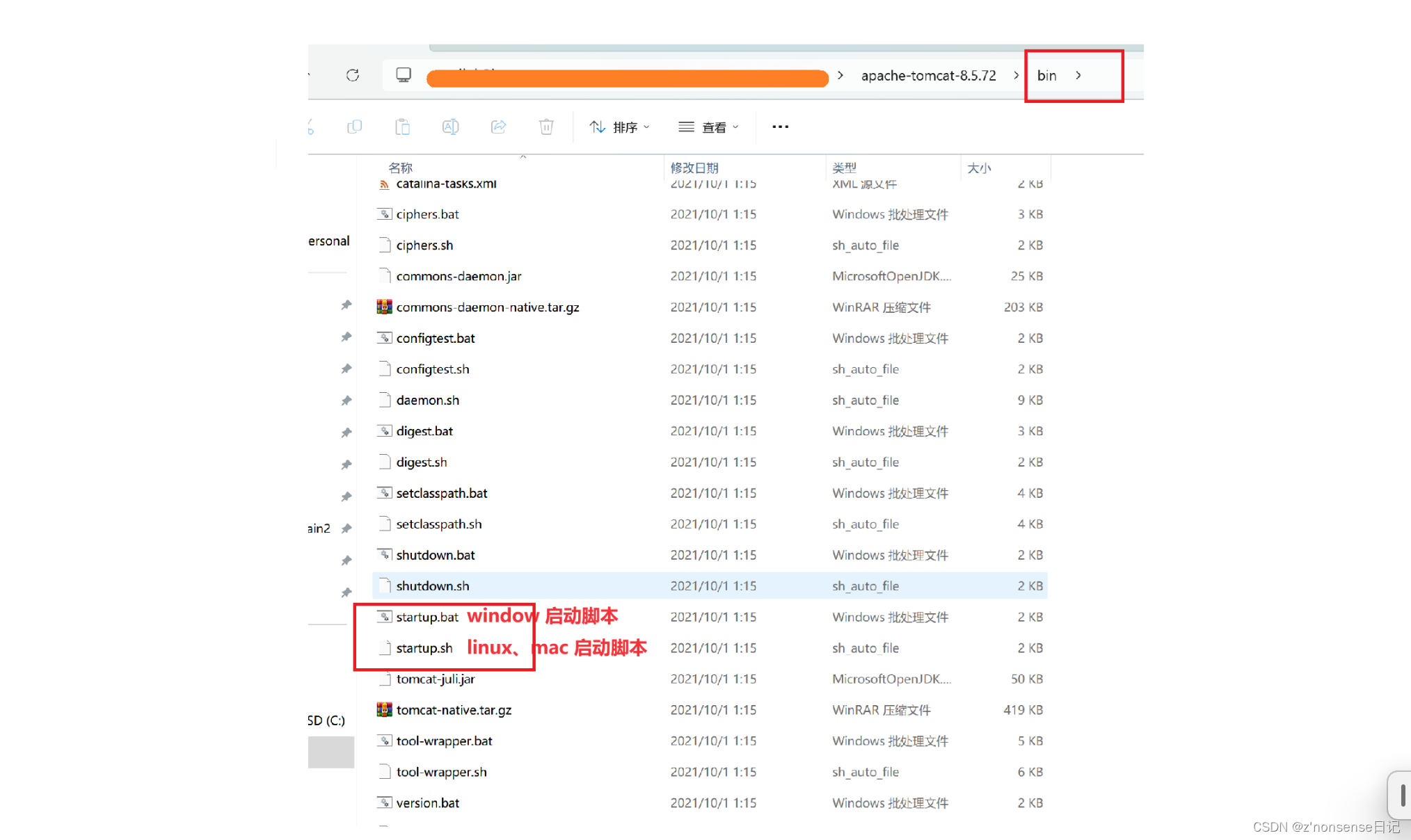
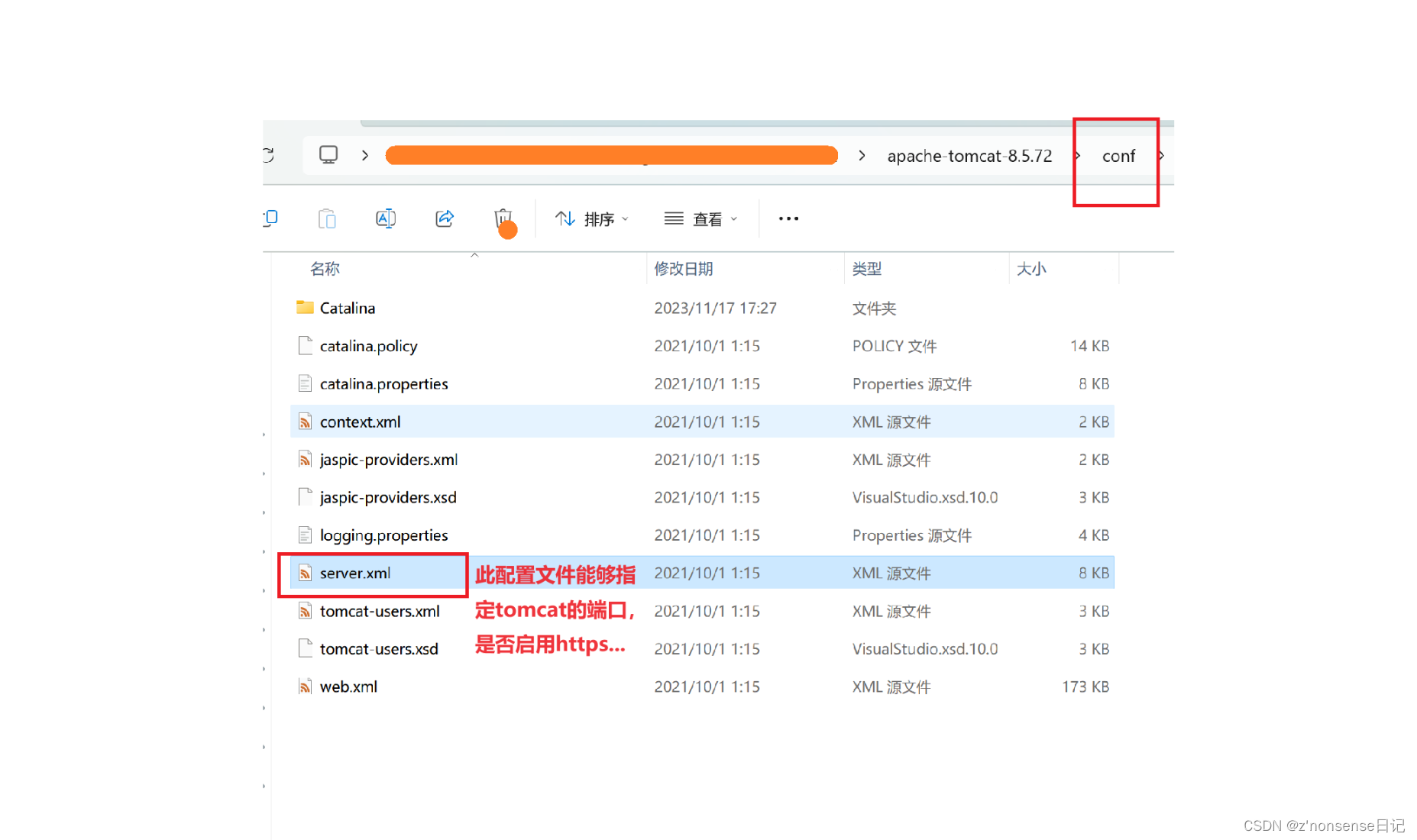
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

2）、双击 start.bat ，启动 tomcat
在这里插入图片描述
启动成功。

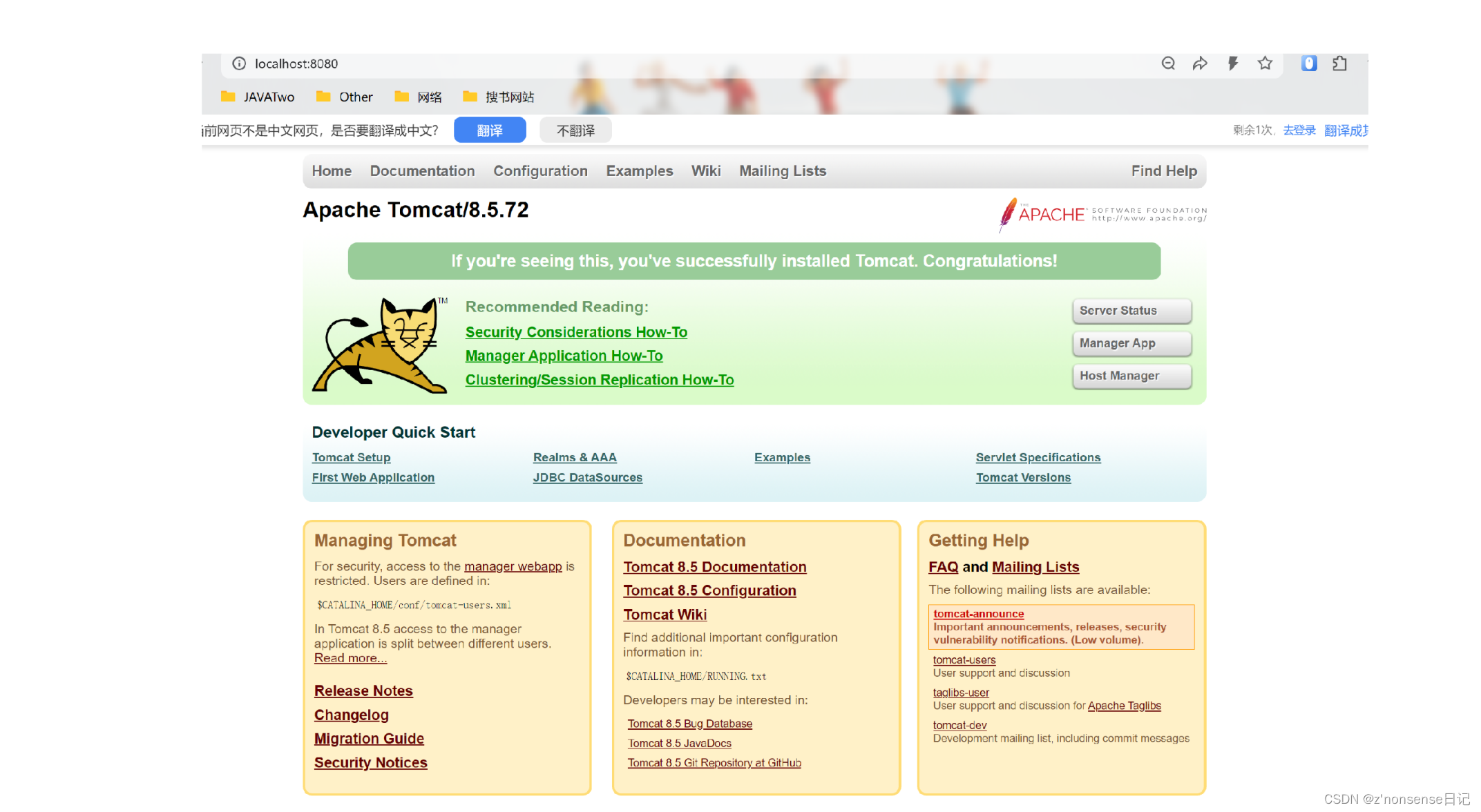
然后在浏览器中输入 127.0.0.1:8080 就可以看到 tomcat 这个欢迎界面了。
在这里插入图片描述

三、使用tomcat访问资源

test.html：

<!DOCTYPE html>
<html lang="en">
<head><meta charset="UTF-8"><meta name="viewport" content="width=device-width, initial-scale=1.0"><title>testhtml</title>
</head>
<body><h1 style="font-weight: 90%; font-size: 90px; color: aquamarine;">hello world!</h1>
</body>
</html>

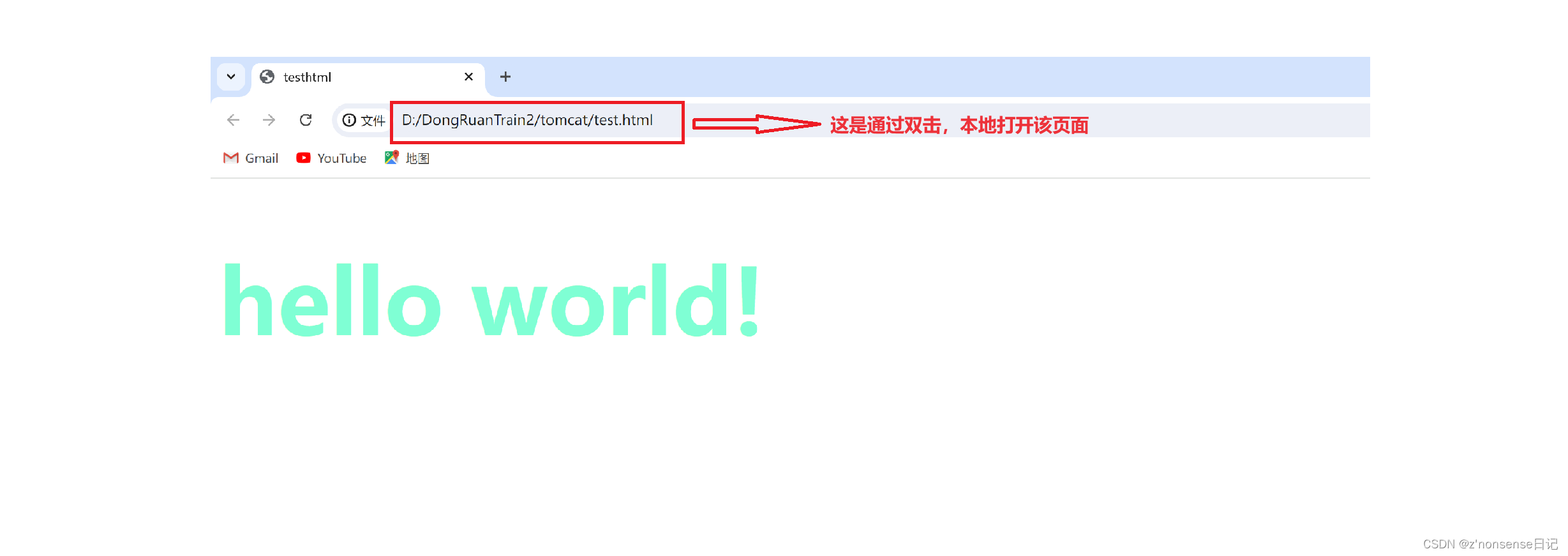
在这里插入图片描述
那我们如何通过 tomcat 的 http 服务器获取到这个页面，而不是直接双击本地打开呢？？

我们需要将这个页面 test.html 放到 tomcat 的 目录webapps 下的 ROOT 目录：
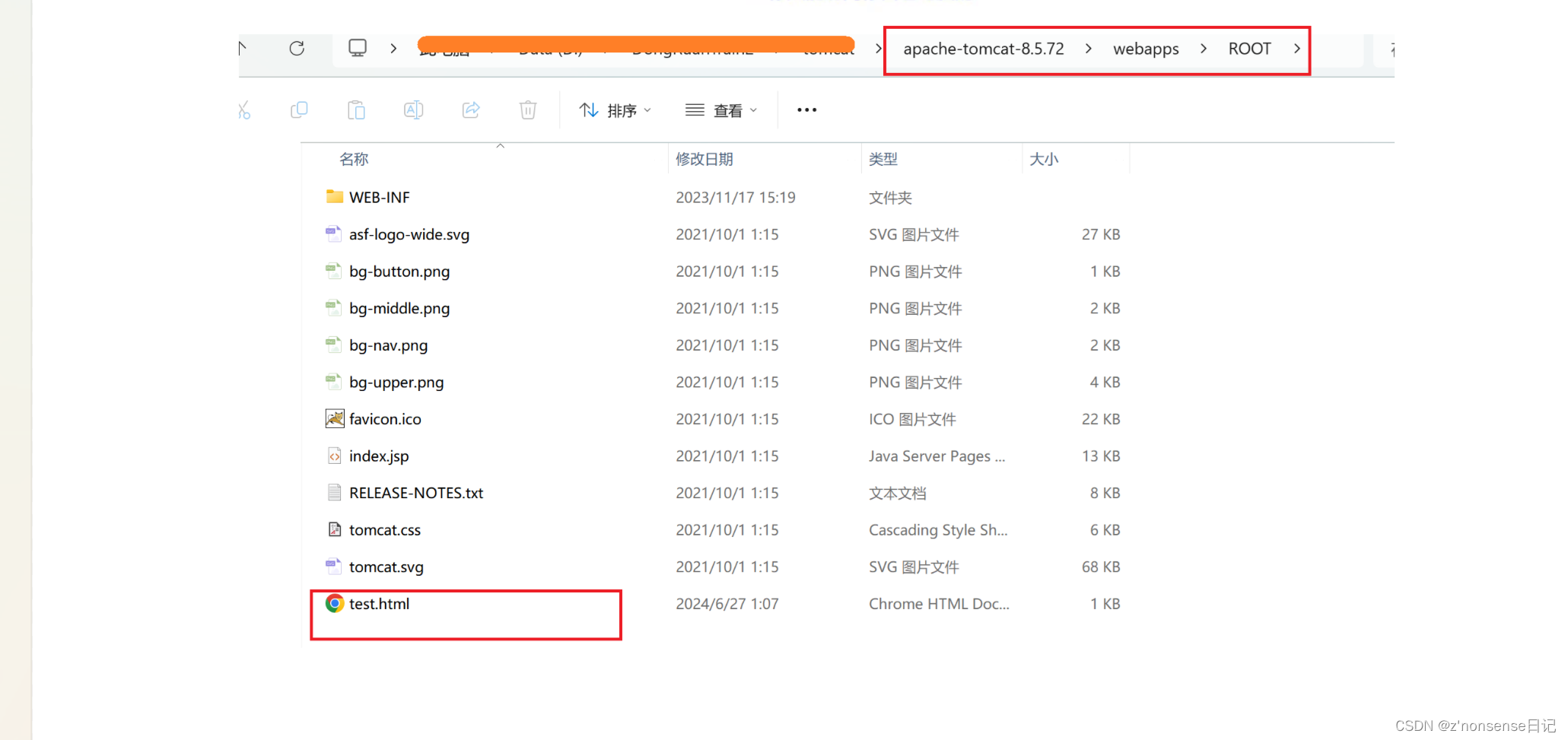
在这里插入图片描述
此时就可以通过 tomcat 的 http服务器访问本机电脑的资源了，而不再是通过
双击打开的方式。
在这里插入图片描述
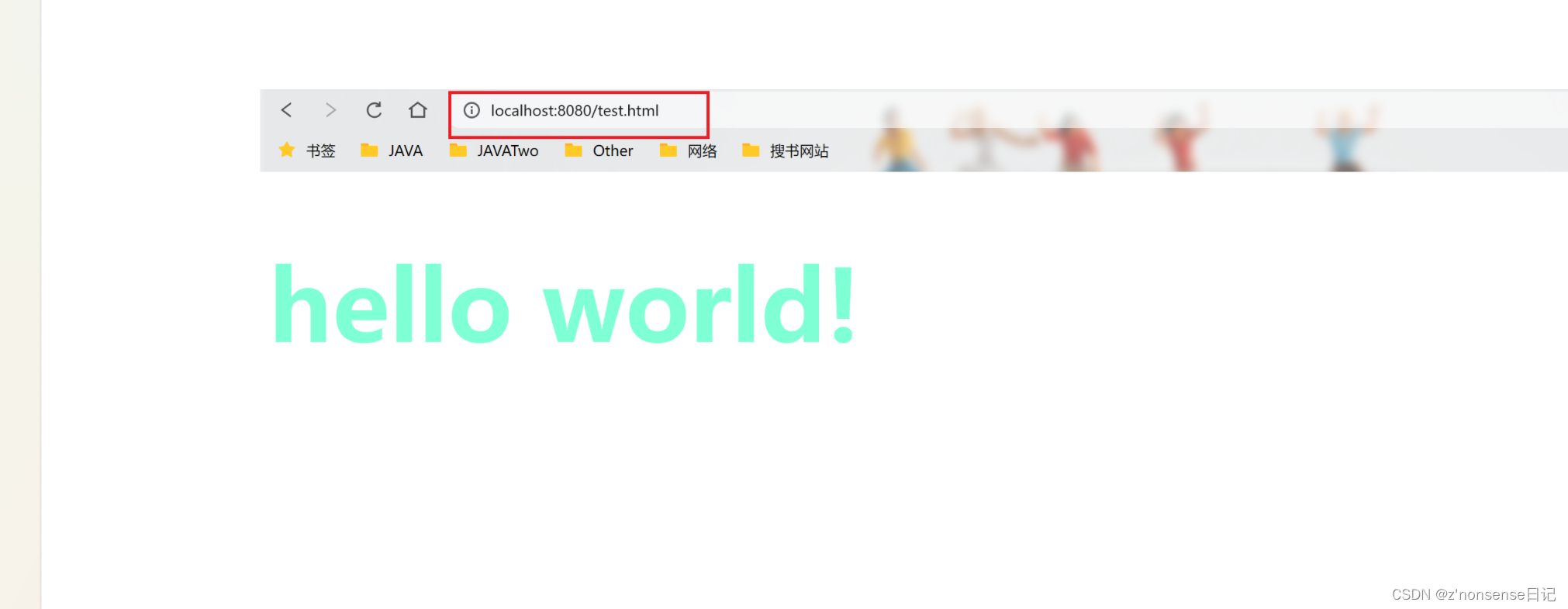
但是既然可以通过双击就能打开此网站，为啥还要通过http服务器访问呢？双击打开时，显示的资源只有你自己能看到，因为此资源只存在你的主机上，但是通过 tomcat ，别人就可以通过这个URL，在他自己的电脑上访问我们主机上的资源，我们也可以访问别人主机上的资源。

但是现在如果你访问我上面这个URL ：localhost:8080/test.html ，你是没办法访问到我的这个网页资源的，这是因为NAT机制，由于在不同的局域网里，ip地址能够重复，因此你没办法访问。当我将tomcat放到云服务器上时，云服务器就会提供一个公网ip，此时才能访问到。

如果资源比较多，可以不用将文件放到 ROOT 目录下，而是在 webapps 目录下创建一个新目录，将文件放在新目录下即可。

相关文章：

浅谈Tomcat

文章目录 一、什么是Tomcat&#xff1f;二、Tomcat的下载安装三、使用tomcat访问资源 一、什么是Tomcat&#xff1f; Tomcat 就是一个 HTTP 服务器。 前面我们聊了HTTP服务器&#xff0c;像我们在网页输入URL&#xff0c;其实就是在给人家的HTTP服务器发送请求&#xff0c;既…...

编程日记 2024/6/27 12:16:00

C++精解【7】

文章目录 eigen矩阵初始化多维矩阵矩阵和向量size固定大小or 动态大小Matrix类六个模板参数初始化向量元素类型 参考文献 eigen 矩阵初始化 多维矩阵 数组 MatrixXi a { // construct a 2x2 matrix{1, 2}, // first row{3, 4} // second row }; Matrix<do…...

编程日记 2024/6/27 12:14:59

堆箱子00

题目链接 堆箱子 题目描述 注意点 将箱子堆起来时&#xff0c;下面箱子的宽度、高度和深度必须大于上面的箱子 解答思路 初始想到深度优先遍历&#xff0c;最后超时了参照题解使用动态规划&#xff0c;先将盒子从小到大进行排序&#xff0c;dp[i]存储的是到第i个箱子时堆箱…...

编程日记 2024/6/27 12:13:58

Linux 命令：iftop

1. 写在前面 本文主要介绍 Linux iftop&#xff08;Interface TOP&#xff09; 命令&#xff1a;iftop 是一款小巧、免费且功能强大的网卡实时流量监控工具。监控指定网卡的实时流量、端口连接信息、反向解析 IP 等&#xff0c;还可以精确显示本机网络流量及网络内各主机和本机…...

编程日记 2024/6/27 12:12:57

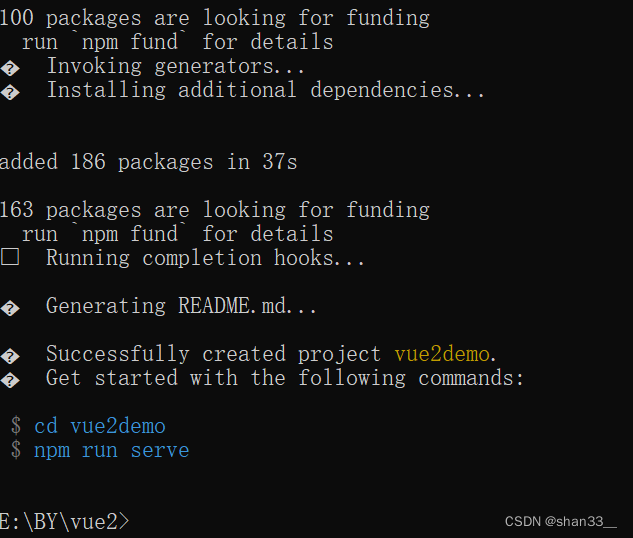
web学习笔记（六十九）vue2

目录 1. vue2创建脚手架项目 2.vue2如何关闭eslint 1. vue2创建脚手架项目 &#xff08;1&#xff09;在cmd窗口输入npm install -g vue/cli命令行&#xff0c;快速搭建脚手架。 &#xff08;2&#xff09; 创建vue2项目 &#xff08;3&#xff09; 选择配置项目&#xff0c…...

编程日记 2024/6/27 12:10:54

JavaScript全解：从基础到高级，掌握每一个知识点

引言&#xff1a; JavaScript是一种广泛使用的脚本语言&#xff0c;主要用于Web浏览器&#xff0c;但近年来也扩展到了服务器端&#xff08;Node.js&#xff09;和其他领域。它允许开发者创建交互式的网页&#xff0c;处理数据&#xff0c;控制用户界面&#xff0c;甚至构建完…...

编程日记 2024/6/27 12:09:53

RabbitMQ的Direct交换机

Direct交换机 BindingKey 在Fanout模式中&#xff0c;一条消息&#xff0c;会被所有订阅的队列都消费。但是&#xff0c;在某些场景下&#xff0c;我们希望不同的消息被不同的队列消费。这时就要用到Direct类型的Exchange。 在Direct模型下&#xff1a; 队列与交换机的绑定&a…...

编程日记 2024/6/27 12:08:52

2024.6.26 待学习知识点

OOALV https://www.cnblogs.com/BruceKing/p/11447499.html " 取工单的组件 lt_aufnr CORRESPONDING #( lt_out MAPPING aufnr aufnr EXCEPT * ). ABAP POPUP_TO_CONFIRM 弹出框函数 CLASS-EVENTS CLASS-METHODS main. CLASS-METHODS raise_event_EXIT_COMMAND IMPOR…...

编程日记 2024/6/27 12:07:50

【LeetCode】每日一题：相交链表

给你两个单链表的头节点 headA 和 headB &#xff0c;请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点&#xff0c;返回 null 。 图示两个链表在节点 c1 开始相交&#xff1a; 题目数据 保证 整个链式结构中不存在环。 注意&#xff0c;函数返回结果后&am…...

编程日记 2024/6/27 12:04:47

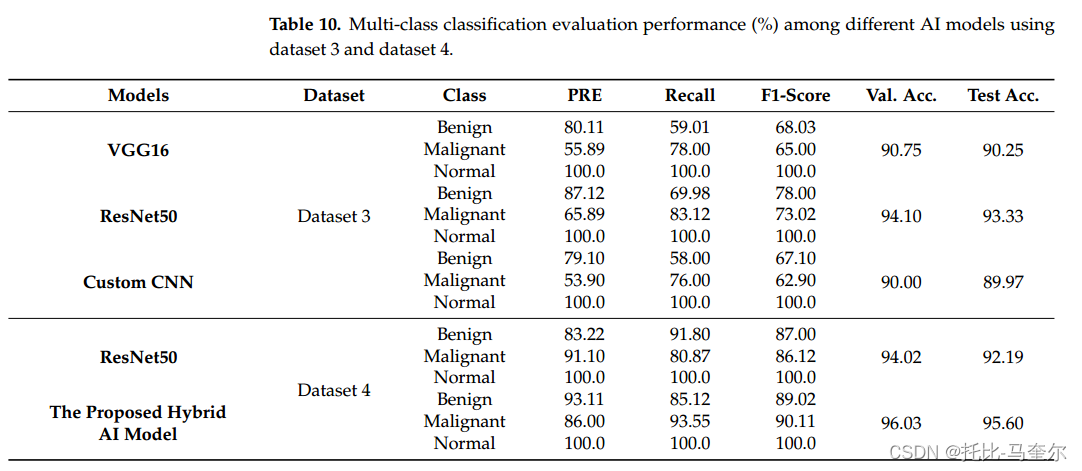
6.26.1 残差卷积变压器编码器的混合工作流程用于数字x线乳房x光片乳腺癌分类

基于残差卷积网络和多层感知器变压器编码器(MLP)的优势&#xff0c;提出了一种新型的混合深度学习乳腺病变计算机辅助诊断(CAD)系统。利用骨干残差深度学习网络创建深度特征&#xff0c;利用Transformer根据自注意力机制对乳腺癌进行分类。所提出的CAD系统具有识别两种情况乳腺…...

编程日记 2024/6/27 12:02:45

[leetcode]avoid-flood-in-the-city 避免洪水泛滥

. - 力扣&#xff08;LeetCode&#xff09; class Solution { public:vector<int> avoidFlood(vector<int>& rains) {vector<int> ans(rains.size(), 1);set<int> st;unordered_map<int, int> mp;for (int i 0; i < rains.size(); i) {i…...

编程日记 2024/6/27 12:01:44

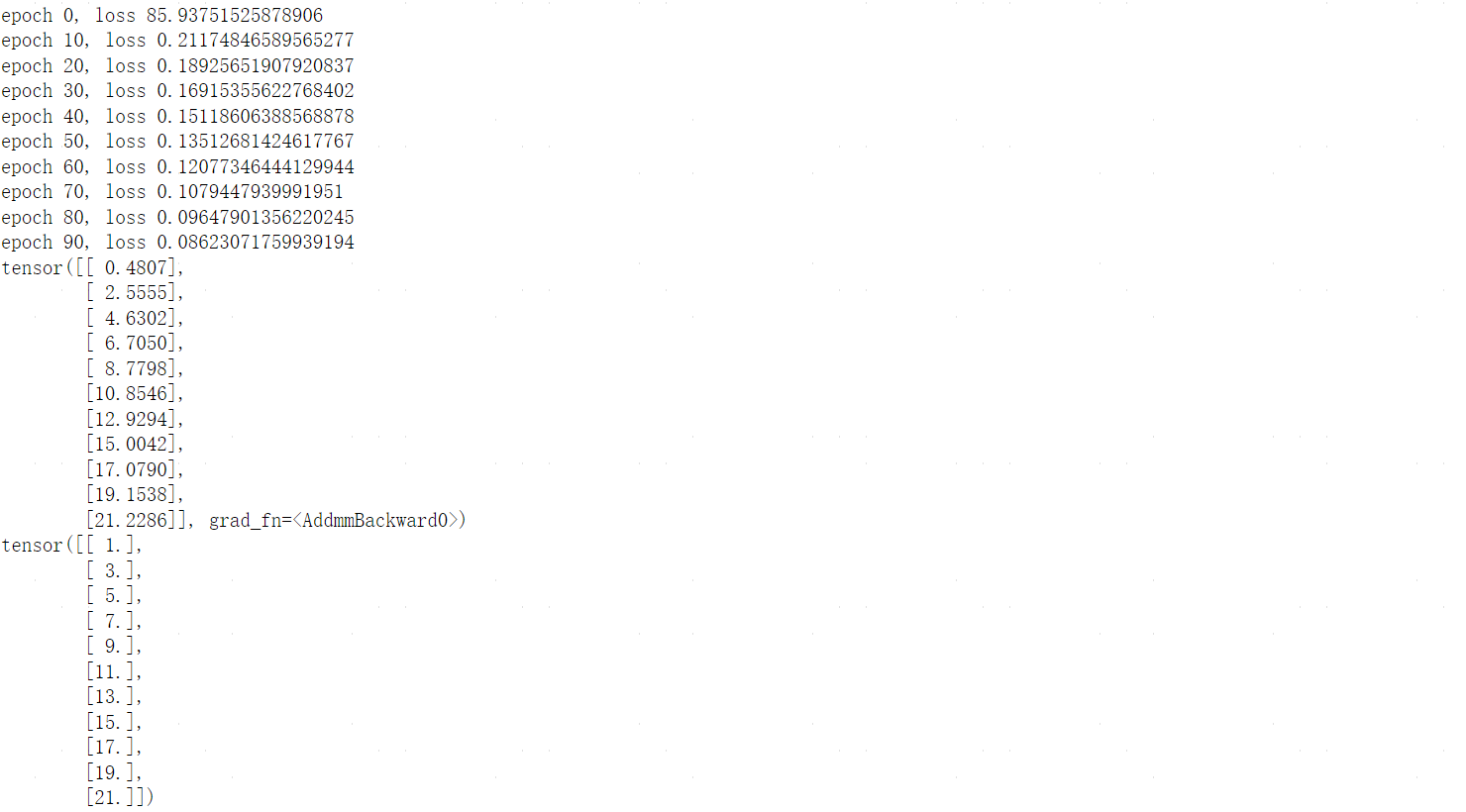
Pytorch基础

文章目录 零、tensorboard0.1基本使用案例 一、数据结构&#xff1a;Tensor1.1数据类型1.2Tensor的创建方式1.3张量的基本运算1.4张量的属性 二、数据集加载器DataLoaders2.0前置知识2.0.1torch.scatter()、torch.scatter_() 2.1官方案例2.1.1从TorchVision加载数据集2.1.2迭代…...

编程日记 2024/6/27 12:00:43

嵌入技术Embedding

嵌入&#xff08;Embedding&#xff09;是一种将高维数据映射到低维空间的技术&#xff0c;广泛应用于自然语言处理&#xff08;NLP&#xff09;、计算机视觉和推荐系统等领域。嵌入技术的核心思想是将复杂的数据表示为低维向量&#xff0c;使其在这个低维空间中保留尽可能多的…...

编程日记 2024/6/27 11:59:41

Pandas中的数据转换[细节]

今天我们看一下Pandas中的数据转换&#xff0c;话不多说直接开始&#x1f387; 目录 一、⭐️apply函数应用 apply是一个自由度很高的函数 对于Series&#xff0c;它可以迭代每一列的值操作&#xff1a; 二、⭐️矢量化字符串 为什么要用str属性 替换和分割 提取子串 …...

编程日记 2024/6/27 11:58:40

vue2面试题——路由

1. 路由的模式和区别 路由的模式&#xff1a;history&#xff0c;hash 区别&#xff1a; 1. 表象不同 history路由&#xff1a;以/为结尾&#xff0c;localhost:8080——>localhost:8080/about hash路由&#xff1a;会多个#&#xff0c;localhost:8080/#/——>localhost:…...

编程日记 2024/6/27 11:56:38

【AI应用探讨】—朴素贝叶斯应用场景

目录 文本分类 推荐系统 信息检索 生物信息学 金融领域 医疗诊断 其他领域 文本分类 垃圾邮件过滤&#xff1a;朴素贝叶斯被广泛用于垃圾邮件过滤任务&#xff0c;通过邮件中的文本内容来识别是否为垃圾邮件。例如&#xff0c;它可以基于邮件中出现的单词或短语的概率来…...

编程日记 2024/6/27 11:55:37

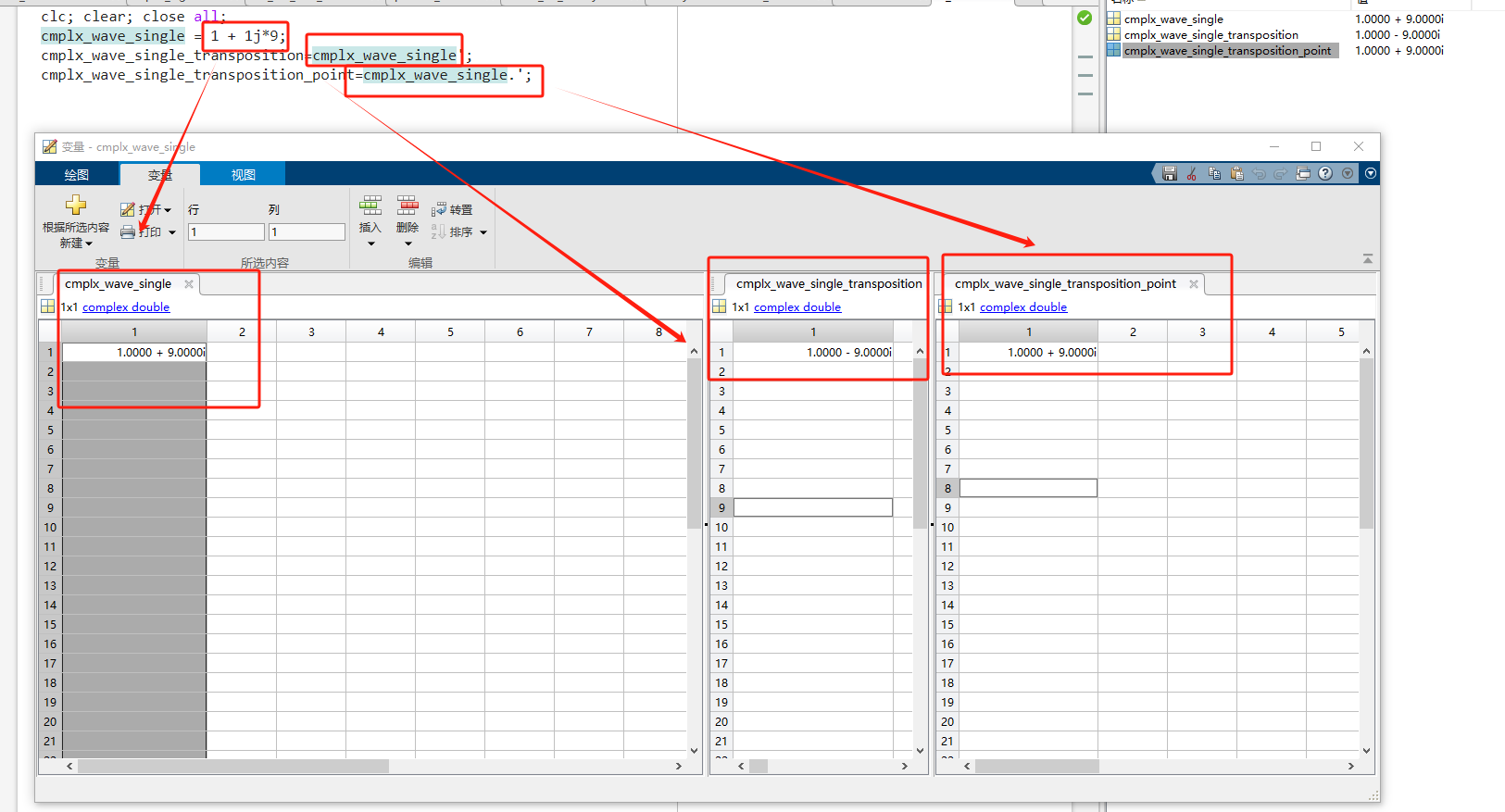
使用matlab的大坑，复数向量转置！！！！！变量区“转置变量“功能（共轭转置）、矩阵转置（默认也是共轭转置）、点转置

近期用verilog去做FFT相关的项目&#xff0c;需要用到matlab进行仿真然后和verilog出来的结果来做对比&#xff0c;然后计算误差。近期使用matlab犯了一个错误&#xff0c;极大的拖慢了项目进展&#xff0c;给我人都整emo了&#xff0c;因为怎么做仿真结果都不对&#xff0c;还…...

编程日记 2024/6/27 11:53:34

昇思25天学习打卡营第8天|保存与加载

1. 学习内容复盘 1.1 保存与加载 上一章节主要介绍了如何调整超参数&#xff0c;并进行网络模型训练。在训练网络模型的过程中&#xff0c;实际上我们希望保存中间和最后的结果&#xff0c;用于微调&#xff08;fine-tune&#xff09;和后续的模型推理与部署&#xff0c;本章…...

编程日记 2024/6/27 11:51:32

【vueUse库Animation模块各函数简介及使用方法】

vueUse库是一个专门为Vue打造的工具库，提供了丰富的功能，包括监听页面元素的各种行为以及调用浏览器提供的各种能力等。其中的Browser模块包含了一些实用的函数，以下是这些函数的简介和使用方法： vueUse库Sensors模块各函数简介及使用方法 vueUseAnimation函数1. useInter…...

编程日记 2024/6/27 11:49:30

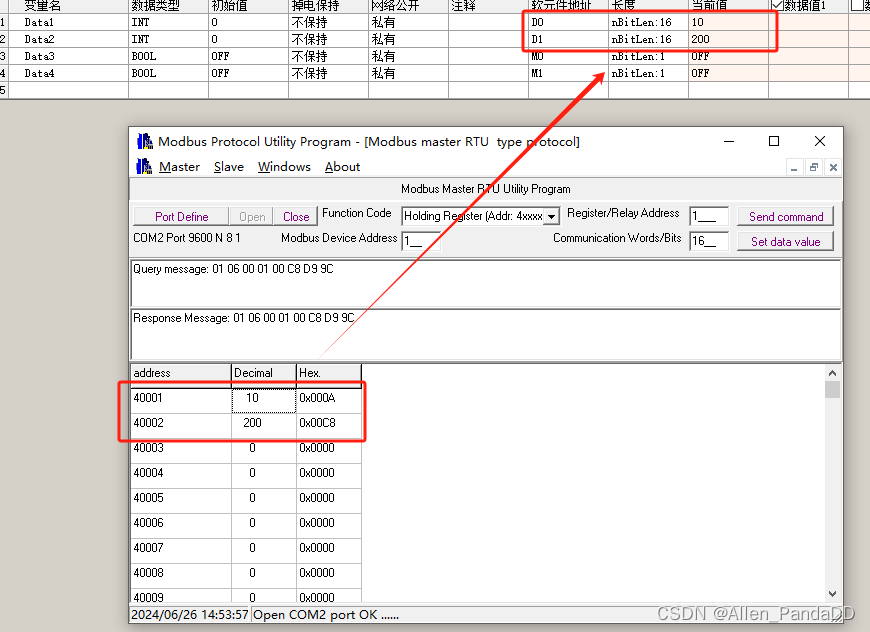
汇川H5u小型PLC作modbusRTU从站设置及测试

目录 新建工程COM通讯参数配置协议选择协议配置 查看手册Modbus地址对应关系仿真测试 新建工程 新建一个H5U工程&#xff0c;不使用临时工程 系列选择H5U即可 COM通讯参数配置 协议选择 选择ModbusRTU从站 协议配置 端口号默认不可选择 波特率这里使用9600 数据长度&…...

编程日记 2024/6/27 11:48:29

MPNet：旋转机械轻量化故障诊断模型详解python代码复现

目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块（MBFM） 2.2 残差注意力金字塔模块（RAPM） 2.2.1 空间金字塔注意力（SPA） 2.2.2 金字塔残差块（PRBlock） 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

编程新知 2026/2/7 5:16:28

React Native 开发环境搭建（全平台详解）

React Native 开发环境搭建&#xff08;全平台详解&#xff09; 在开始使用 React Native 开发移动应用之前&#xff0c;正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南&#xff0c;涵盖 macOS 和 Windows 平台的配置步骤&#xff0c;如何在 Android 和 iOS…...

编程新知 2025/10/7 2:47:54

苍穹外卖--缓存菜品

1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得&#xff0c;如果用户端访问量比较大&#xff0c;数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据&#xff0c;减少数据库查询操作。 缓存逻辑分析&#xff1a; ①每个分类下的菜品保持一份缓存数据…...

编程新知 2026/2/7 15:39:49

【Zephyr 系列 10】实战项目：打造一个蓝牙传感器终端 + 网关系统（完整架构与全栈实现）

🧠关键词：Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者：希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数：约 5200 字 ✨ 项目总览 在物联网实际项目中，**“终端 + 网关”**是…...

编程新知 2026/1/31 6:12:22

【Redis】笔记｜第8节｜大厂高并发缓存架构实战与优化

缓存架构 代码结构 代码详情 功能点&#xff1a; 多级缓存&#xff0c;先查本地缓存&#xff0c;再查Redis&#xff0c;最后才查数据库热点数据重建逻辑使用分布式锁&#xff0c;二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

编程新知 2026/1/26 3:45:28

RabbitMQ入门4.1.0版本（基于java、SpringBoot操作）

RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发&#xff0c;后来由Pivotal Software Inc.&#xff08;现为VMware子公司&#xff09;接管。RabbitMQ 是一个开源的消息代理和队列服务器&#xff0c;用 Erlang 语言编写。广泛应用于各种分布…...

编程新知 2026/1/31 3:52:49

9-Oracle 23 ai Vector Search 特性 知识准备

很多小伙伴是不是参加了 免费认证课程&#xff08;限时至2025/5/15&#xff09; Oracle AI Vector Search 1Z0-184-25考试&#xff0c;都顺利拿到certified了没。 各行各业的AI 大模型的到来&#xff0c;传统的数据库中的SQL还能不能打&#xff0c;结构化和非结构的话数据如何和…...

编程新知 2026/2/7 23:29:43

GraphQL 实战篇：Apollo Client 配置与缓存

GraphQL 实战篇&#xff1a;Apollo Client 配置与缓存 上一篇&#xff1a;GraphQL 入门篇&#xff1a;基础查询语法 依旧和上一篇的笔记一样&#xff0c;主实操&#xff0c;没啥过多的细节讲解&#xff0c;代码具体在&#xff1a; https://github.com/GoldenaArcher/graphql…...

编程新知 2026/2/6 5:45:36

Vue3中的computer和watch

computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...

编程新知 2025/11/8 20:34:42

文件上传漏洞防御全攻略

要全面防范文件上传漏洞&#xff0c;需构建多层防御体系&#xff0c;结合技术验证、存储隔离与权限控制&#xff1a; &#x1f512; 一、基础防护层 前端校验&#xff08;仅辅助&#xff09; 通过JavaScript限制文件后缀名&#xff08;白名单&#xff09;和大小&#xff0c;提…...

编程新知 2025/8/18 19:05:00