似然 与 概率

似然与概率分别是针对不同内容的估计和近似

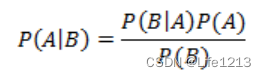
概率

概率：概率表达给定参数 $\theta$下样本随机向量$\text{X}=x$的可能性。

概率密度函数的定义形式是 $f(x|\theta )$，即概率密度函数是在"已知" θ 的情况下,去估计样本随机变量 x 出现的可能性.

似然

似然：给定样本$\text{X}=x$下，参数$\theta ={\theta }_1$（相对于另外的参数取值）为真实值的可能性。
单独的似然值没有意义，似然值L是用来对比在各种θi下，哪种θi更接近与引发事件x的真实的“θ”

似然函数的形式是$L(\theta \mid x)$，其中"|"代表的是条件概率或者条件分布。似然函数是在已知 样本随机变量 $\text{X}=x$的情况下，估计 参数θ 的值，是参数 θ 的函数。即改变θ，选择到 X=x 的可能性在改变。

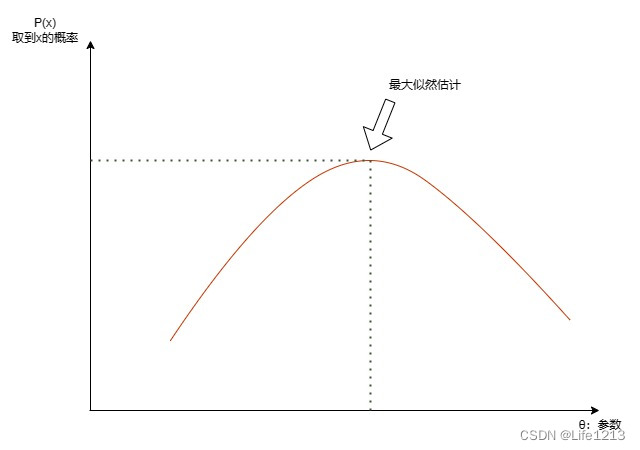
$L(\theta 1\mid x)>L(\theta 2\mid x)$：在参数θ1下取到 X=x 的可能性大于 在参数θ2下取到 X=x 的可能性，即参数θ1为真实参数的可能性大于参数θ2为真实参数的可能性。

注意一些概念的理解：

1. 样本随机变量的出现是基于某个分布的.例如$f(x|\theta )$代表x服从f 分布,而f 的分布是由参数 θ 决定的。参数θ刻画了随机变量 X 在概率空间中服从什么分布。
2. 在概率统计学中$\text{X}$代表的是随机变量,而小写形式x通常代表其具体取值.

概率函数与似然函数的关系

在函数的结构上，概率函数与似然函数长的是一样的，只是固定的值与自变量不同

$f(x|\theta )=L(\theta |x)$=由 x与θ 所构成的式子。

若X为离散的随机样本，可以将函数改写为：
$f(x|\theta )=L(\theta |x)=P_{\theta }(X=x)$

似然与机器学习的关系

在机器学习中，之所以需要似然函数函数的概念，是因为我们往往是想要机器根据已有的数据学到相应的分布。即在训练阶段, 是根据已有的数据 X 来估计其真实的数据分布服从什么样的分布θ
而在测试阶段, 就是已知参数θ, 来估计该分布下, X应该是什么.

最大似然估计

在模型训练时，我希望找到参数θ，在这个参数下得到样本X的可能性达到最大，即参数θ为真实值的可能性达到最大，把这个参数作为估计的真实值。

而这个参数是通过似然函数得到的。