当前位置： 首页 > news >正文

【监控】3.配置 Grafana 以使用 Prometheus 数据源

news 2026/2/8 0:52:14

1 访问 Grafana

打开浏览器，访问 http://localhost:3000（默认端口）。使用默认的用户名和密码 admin/admin 登录。

2 添加 Prometheus 数据源

  • 进入 Grafana 仪表板，点击左侧菜单中的“Configuration” -> “Data Sources”。
  • 点击 “Add data source” 按钮。
  • 选择 “Prometheus” 作为数据源类型。
  • 在 “URL” 字段中输入 Prometheus 服务器地址，例如 http://localhost:9090。
  • 点击 “Save & Test” 按钮以保存配置并测试连接。

3 创建仪表板

  • 在 Grafana 中点击左侧菜单中的 “Create” -> “Dashboard”。
  • 添加新面板（Panel），选择你的 Prometheus 数据源并输入 PromQL 查询来获取 Java 服务的指标。
  • 配置图表的显示方式，然后保存仪表板。

相关文章：

【监控】3.配置 Grafana 以使用 Prometheus 数据源

1 访问 Grafana 打开浏览器，访问 http://localhost:3000（默认端口）。使用默认的用户名和密码 admin/admin 登录。 2 添加 Prometheus 数据源 进入 Grafana 仪表板，点击左侧菜单中的“Configuration” -> “Data Sources”。…...

编程日记 2024/6/28 3:54:04

【LinuxC语言】网络编程中粘包问题

文章目录 前言什么叫做粘包问题粘包问题如何解决？总结前言 在进行网络编程时，我们经常会遇到一个非常常见但又往往被忽视的问题，那就是"粘包"问题。粘包是指在基于TCP/IP协议的数据传输过程中，由于TCP/IP协议是基于字节流的，这就可能会导致多个数据包被一起接收…...

编程日记 2024/6/28 3:53:03

Docker之jekins的安装

jekins官网地址：Jenkins Plugins （https://plugins.jenkins.io/） jekins 的docker 官方地址：https://hub.docker.com/r/jenkins/jenkins jekins 的docker 允许命令文档地址： docker/README.md at master jenkinsci…...

编程日记 2024/6/28 3:51:01

# bash: chkconfig: command not found 解决方法

bash: chkconfig: command not found 解决方法 一、chkconfig 错误描述： 这个错误表明在 Bash 环境下，尝试执行 chkconfig 命令，但是系统找不到这个命令。chkconfig 命令是一个用于管理 Linux 系统中服务的启动和停止的工具，通常…...

编程日记 2024/6/28 3:50:00

Linux线程互斥锁

目录 🚩看现象，说原因 🚩解决方案 🚩互斥锁 🚀关于互斥锁的理解 🚀关于原子性的理解 🚀如何理解加锁和解锁是原子的 🚩对互斥锁的简单封装 引言 大家有任何疑问，可…...

编程日记 2024/6/28 3:48:59

展开说说：Android列表之RecyclerView

RecyclerView 它是从Android5.0出现的全新列表组件，更加强大和灵活。用于显示列表形式 (list) 或者网格形式 (grid) 的数据，替代ListView和GridView成为Android主流的列表组件。可以说Android客户端只要有表格的地方就有RecyclerView。 RecyclerView 内…...

编程日记 2024/6/28 3:47:58

等保2.0时，最常见的挑战是什么？

等保2.0的常见挑战 等保2.0（网络安全等级保护2.0）是中国网络安全领域的基本制度，它对信息系统进行分级分类、安全保护和安全测评，以提高信息系统的安全性和可信性。在等保2.0的实施过程中，企业和组织面临多方面的挑战&…...

编程日记 2024/6/28 3:46:56

基于Vue 3.x与TypeScript的PPTIST本地部署与无公网IP远程演示文稿

文章目录 前言1. 本地安装PPTist2. PPTist 使用介绍3. 安装Cpolar内网穿透4. 配置公网地址5. 配置固定公网地址 前言 本文主要介绍如何在Windows系统环境本地部署开源在线演示文稿应用PPTist，并结合cpolar内网穿透工具实现随时随地远程访问与使用该项目。 PPTist …...

编程日记 2024/6/28 3:45:55

PHP的基本语法有哪些？

PHP的基本语法包括以下几个方面&#xff1a; PHP标记&#xff1a;PHP脚本以<?php开始&#xff0c;以?>结束。这是PHP文件的默认文件扩展名是.php。 变量和常量&#xff1a;变量以$符号开头&#xff0c;其后是变量的名称。常量使用define()函数定义&#xff0c;例如def…...

编程日记 2024/6/28 3:43:52

CSS的媒体查询：响应式布局的利器

关于CSS的媒体查询 CSS媒体查询是CSS层叠样式表(Cascading Style Sheets)中的一个核心功能&#xff0c;它使得开发者能够根据不同的设备特性和环境条件来应用不同的样式规则。这是实现响应式网页设计的关键技术&#xff0c;确保网站或应用能够在多种设备上&#xff0c;包括桌面…...

编程日记 2024/6/28 3:42:51

汇聚荣做拼多多运营第一步是什么？

汇聚荣做拼多多运营第一步是什么?在众多电商平台中&#xff0c;拼多多凭借其独特的社交电商模式迅速崛起&#xff0c;吸引了大量消费者和商家的目光。对于希望在拼多多上开店的商家而言&#xff0c;了解如何进行有效运营是成功的关键。那么&#xff0c;汇聚荣做拼多多运营的第…...

编程日记 2024/6/28 3:41:51

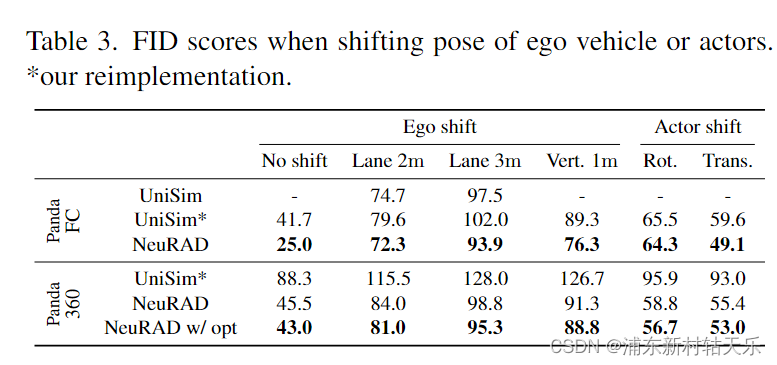
NeRF从入门到放弃4: NeuRAD-针对自动驾驶场景的优化

NeuRAD: Neural Rendering for Autonomous Driving 非常值得学习的一篇文章&#xff0c;几乎把自动驾驶场景下所有的优化都加上了&#xff0c;并且也开源了。 和Unisim做了对比&#xff0c;指出Unisim使用lidar指导采样的问题是lidar的垂直FOV有限&#xff0c;高处的东西打不…...

编程日记 2024/6/28 3:39:49

docker环境部署ruoyi系统前后端分离项目

创建局域网 docker network create net-ry 安装Redis 1 安装 创建两个目录 mkdir -p /data/redis/{conf,data} 上传redis.conf文件到/data/redis/conf文件夹中 cd /data/redis/conf 3.2 配置redis.conf文件 配置redis.conf文件&#xff1a; redis.conf文件配置注意&…...

编程日记 2024/6/28 3:38:48

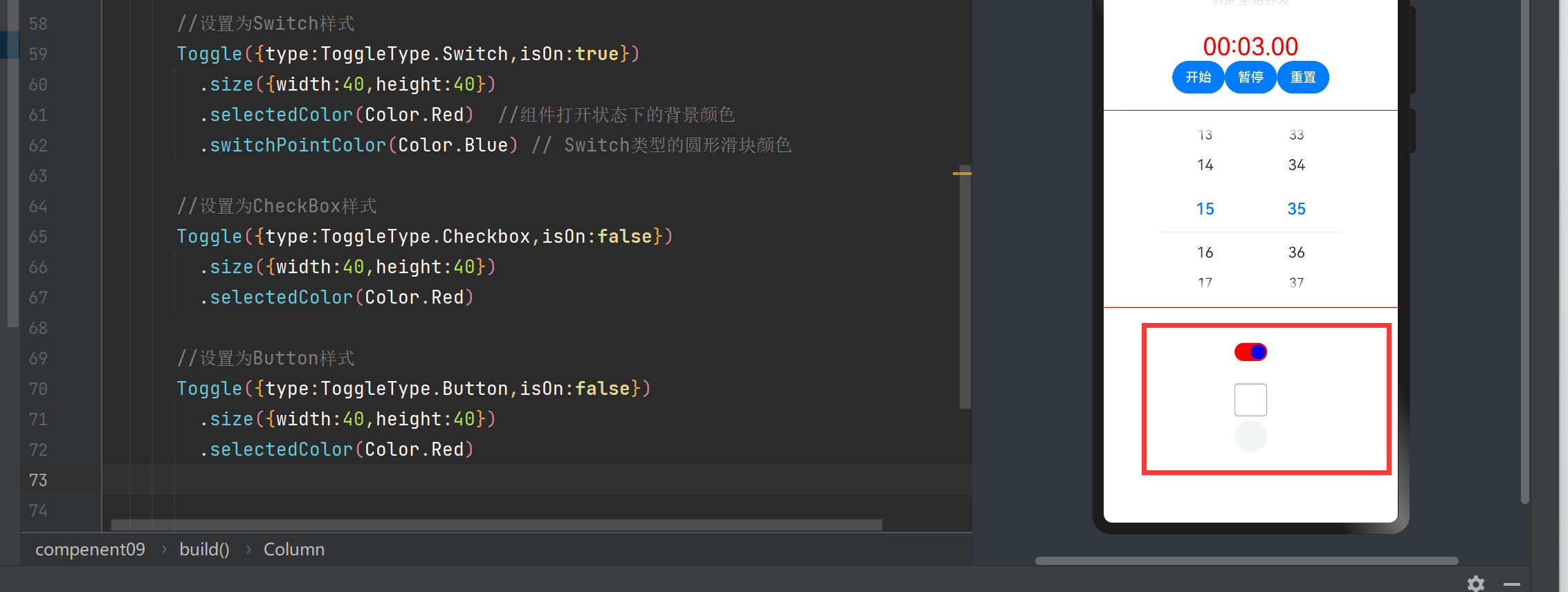
UI（二）控件

文章目录 PatternLockProgressQRCodeRadioRatingRichTextScollBarSearchSelectSlideSpanStepper和StepperItemTextTextAreaTextClockTextInputTextPickerTextTimerTimePickerToggleWeb PatternLock PatternLock是图案密码锁组件&#xff0c;以九宫格图案的方式输入密码&#x…...

编程日记 2024/6/28 3:37:47

【图像分类】Yolov8 完整教程 |分类 |计算机视觉

目标&#xff1a;用YOLOV8进行图像分类。 图像分类器。 学习资源&#xff1a;https://www.youtube.com/watch?vZ-65nqxUdl4 努力的小巴掌 记录计算机视觉学习道路上的所思所得。 1、文件结构化 划分数据集&#xff1a;train,val,test 知道怎么划分数据集很重要。 文件夹…...

编程日记 2024/6/28 3:33:43

PyCharm 2024.1最新变化

PyCharm 2024.1 版本带来了一系列激动人心的新功能和改进&#xff0c;以下是一些主要的更新亮点: Hugging Face 模型和数据集文档预览&#xff1a;在 PyCharm 内部快速获取 Hugging Face 模型或数据集的详细信息&#xff0c;通过鼠标悬停或使用 F1 键打开文档工具窗口来预览。 …...

编程日记 2024/6/28 3:32:42

金融行业专题｜某头部期货基于 K8s 原生存储构建自服务数据库云平台

为了进一步提升资源交付效率&#xff0c;不少用户都将数据库应用从物理环境迁移到容器环境。而对于 Kubernetes 部署环境&#xff0c;用户不仅需要考虑数据库在性能方面的需求&#xff0c;还要为数据存储提供更安全、可靠的高可用保障。 近期&#xff0c;某头部期货机构基于 S…...

编程日记 2024/6/28 3:31:41

DELL服务器 OpenManage监控指标解读

监控易是一款专业的IT基础设施监控软件&#xff0c;通过SNMP等多种方式&#xff0c;实时监控服务器、网络设备等IT资源的各项性能指标。对于DELL服务器 OpenManage&#xff0c;监控易提供了全面的监控解决方案&#xff0c;确保服务器的稳定运行。 一、网络连通性监控&#xff…...

编程日记 2024/6/28 3:30:40

vscode下无法识别node、npm的问题

node : 无法将“node”项识别为 cmdlet、函数、脚本文件或可运行程序的名称 因为node是在cmd安装的&#xff0c;是全局安装的&#xff0c;并不是在这个项目里安装的。 解决方案&#xff1a; 1.在vscode的控制台&#xff0c;针对一个项目安装特定版本的node&#xff1b; 2.已经…...

编程日记 2024/6/28 3:29:39

C语言之字符串处理函数

文章目录 1 字符串处理函数1.1 输入输出1.1.1 输出函数puts1.1.2 输入函数gets 1.2 连接函数1.2.1 stract1.2.2 strncat 1.3 复制1.3.1 复制strcpy1.3.2 复制strncpy1.3.3 复制memcpy1.3.4 指定复制memmove1.3.5 指定复制memset1.3.6 新建复制strdup1.3.7 字符串设定strset 1.4…...

编程日记 2024/6/28 3:28:38

业务系统对接大模型的基础方案：架构设计与关键步骤

业务系统对接大模型&#xff1a;架构设计与关键步骤 在当今数字化转型的浪潮中&#xff0c;大语言模型&#xff08;LLM&#xff09;已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中&#xff0c;不仅可以优化用户体验&#xff0c;还能为业务决策提供…...

编程新知 2026/2/4 3:14:18

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型

CVPR 2025 | MIMO&#xff1a;支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题&#xff1a;MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者&#xff1a;Yanyuan Chen, Dexuan Xu, Yu Hu…...

编程新知 2025/10/6 14:17:21

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?

论文网址&#xff1a;pdf 英文是纯手打的&#xff01;论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误&#xff0c;若有发现欢迎评论指正&#xff01;文章偏向于笔记&#xff0c;谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

编程新知 2026/2/6 14:42:11

学习STC51单片机31（芯片为STC89C52RCRC）OLED显示屏1

每日一言 生活的美好&#xff0c;总是藏在那些你咬牙坚持的日子里。 硬件&#xff1a;OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写&#xff0c;"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

编程新知 2026/1/30 4:16:26

vue3 定时器-定义全局方法 vue+ts

1.创建ts文件 路径&#xff1a;src/utils/timer.ts 完整代码&#xff1a; import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

编程新知 2025/8/9 0:31:20

k8s业务程序联调工具-KtConnect

概述 原理 工具作用是建立了一个从本地到集群的单向VPN&#xff0c;根据VPN原理&#xff0c;打通两个内网必然需要借助一个公共中继节点&#xff0c;ktconnect工具巧妙的利用k8s原生的portforward能力&#xff0c;简化了建立连接的过程&#xff0c;apiserver间接起到了中继节…...

编程新知 2026/2/1 4:14:14

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)

文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

编程新知 2026/1/31 23:44:39

全面解析各类VPN技术：GRE、IPsec、L2TP、SSL与MPLS VPN对比

目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec&#xff1f; IPsec VPN 5.1 IPsec传输模式&#xff08;Transport Mode&#xff09; 5.2 IPsec隧道模式&#xff08;Tunne…...

编程新知 2025/11/3 0:44:41

3-11单元格区域边界定位(End属性)学习笔记

返回一个Range 对象&#xff0c;只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意&#xff1a;它移动的位置必须是相连的有内容的单元格…...

编程新知 2026/1/20 19:15:45

智能分布式爬虫的数据处理流水线优化：基于深度强化学习的数据质量控制

在数字化浪潮席卷全球的今天&#xff0c;数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具&#xff0c;在大规模数据获取中发挥着关键作用。然而&#xff0c;传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时&#xff0c;常出现数据质…...

编程新知 2026/2/6 1:04:23