B1048 数字加密
decription
本题要求实现一种数字加密方法。首先固定一个加密用正整数 A,对任一正整数 B,将其每 1 位数字与 A 的对应位置上的数字进行以下运算:对奇数位,对应位的数字相加后对 13 取余——这里用 J 代表 10、Q 代表 11、K 代表 12;对偶数位,用 B 的数字减去 A 的数字,若结果为负数,则再加 10。这里令个位为第 1 位。
输入格式:
输入在一行中依次给出 A 和 B,均为不超过 100 位的正整数,其间以空格分隔。
输出格式:
在一行中输出加密后的结果。
输入样例:
1234567 368782971
输出样例:
3695Q8118
idea
- 个位为第一位,依次
- 奇数位=(b[i]+a[i])%13
- 偶数位=(b[i]-a[i]) > 0 ? (b[i] - a[i]) : (b[i] - a[i] + 10)
- 隐含的细节有
- 字符串a和b可能不等长,短的哪个用0补充
- 在补充0的同时,数组长度改变,需要先记录数组长度
solution(失败版)
最高位为第一位版本
调着调着忘了是各位是第一位,很神奇的可以过测试点1, 2,3
#include <stdio.h>
#include <string.h>
int main(){char a[101], b[101], t[101], hash[14] = "0123456789JQK";int result[101], n = 0, len;scanf("%s%s", a, b);len = strlen(a) - strlen(b);if(len > 0){for(int i = strlen(a) - 1; i >= 0; i--){if(i <= (len - 1)) b[i] = '0';else b[i] = b[i - len];}}else if(len < 0){len *= -1;for(int i = strlen(b) - 1; i >= 0; i--){if(i <= (len - 1)) a[i] = '0';else a[i] = a[i - len];}}for(int i = 0; i < strlen(a) || i < strlen(b); i++, n++){if(i % 2 == 0) result[n] = ((a[i] - '0') + (b[i] - '0')) % 13;else{result[n] = (b[i] - '0') - (a[i] - '0');if(result[n] < 0) result[n] += 10;}}for(int i = 0; i < n; i++) printf("%c", hash[result[i]]);return 0;
}
solution
#include <stdio.h>
#include <string.h>
void reverse(char a[]){for(int i = 0; i < strlen(a) / 2; i++){char c = a[i];a[i] = a[strlen(a) - 1 - i];a[strlen(a) - 1 - i] = c;}
}
int main(){char a[101], b[101], hash[14] = "0123456789JQK";int result[101], n = 0;scanf("%s %s", a, b);reverse(a);reverse(b);int la = strlen(a), lb = strlen(b);for(int i = 0; i < la || i < lb; i++, n++){if(i >= la) a[i] = '0';if(i >= lb) b[i] = '0';if(i % 2 == 0) result[n] = ((a[i] - '0') + (b[i] - '0')) % 13;else{result[n] = (b[i] - '0') - (a[i] - '0');if(result[n] < 0) result[n] += 10;}}for(int i = n - 1; i >= 0; i--) printf("%c", hash[result[i]]);return 0;
}
反思
不能坐在书桌前摸鱼,明确好题设及可能的坑想,不能用低效率decode换个把盲点。
相关文章:

B1048 数字加密
decription 本题要求实现一种数字加密方法。首先固定一个加密用正整数 A,对任一正整数 B,将其每 1 位数字与 A 的对应位置上的数字进行以下运算:对奇数位,对应位的数字相加后对 13 取余——这里用 J 代表 10、Q 代表 11、K 代表 …...

Qt使用FFmpeg播放视频
一、使用场景 因为项目中需要加载MP4播放开机视频,而我们的设备所使用的架构为arm架构,其中缺乏一些多媒体库。安装这些插件库比较麻烦,所以最终决定使用FFmpeg播放视频。 二、下载编译ffmpeg库 2.1 下载源码 源码下载路径:http…...
Win32 ListBox控件
Win32 ListBox控件 创建ListBox控件 创建窗口函数 HWND CrateWindowEx(DWORD dwExStyle , // 窗口的扩展风格,基本没用LPCTSTR lpClassName, // 已经注册的窗口类名称LPCTSTR lpWindowName, // 窗口标题栏的名字DWORD dwStyle, // 窗口的基本风格int x, // 左上角水平坐标int …...
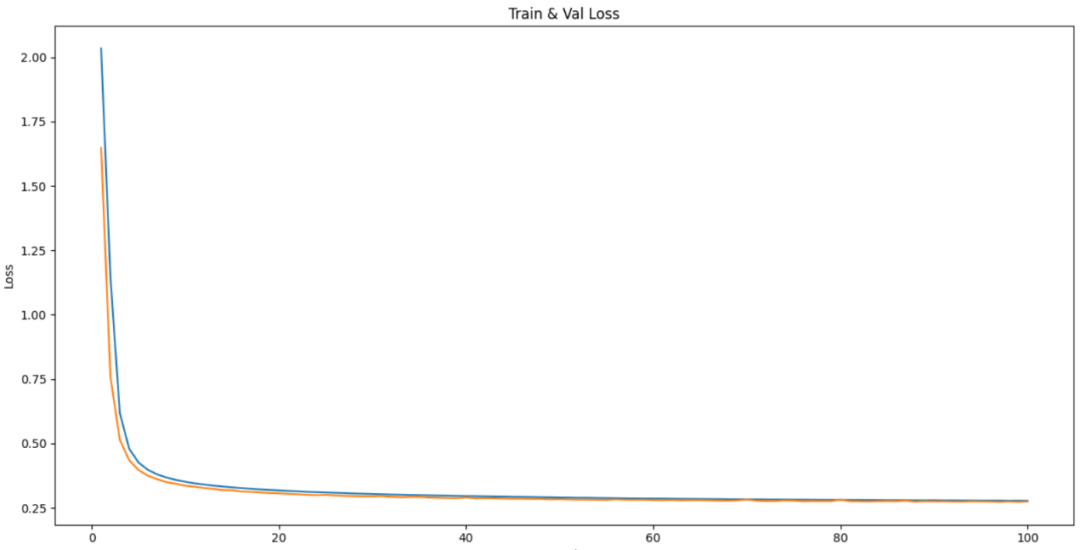
最大值池化与均值池化比较分析
1 问题在深度学习的卷积网络过程中,神经网络有卷积层,池化层,全连接层。而池化层有最大值池化和均值池化两种情况,而我们组就在思考,最大值池化和均值池化有什么区别呢?两者的模型准确率是否有所不同&#…...

统计学 多元线性回归
文章目录统计学 多元线性回归多元线性回归模型拟合优度显著性检验线性关系检验回归系数检验多重共线性及其处理多重共线性的问题多重共线性的识别与处理变量选择利用回归方程进行预测哑变量回归统计学 多元线性回归 多元线性回归模型 多元线性回归模型:设因变量为…...
tar和gzip压缩和解压
打包和压缩的区别:打包:将多文件 封装在一起压缩:将多文件 封装在一起 通过特定的算法 将冗余的数据 进行删除tar默认是打包命令,如果想用tar进行压缩 必须加选项1、gzip格式压缩:tar zcvf 压缩包包名 文件1 文件2 文件…...

搭建Docker企业私有仓库
什么是仓库 仓库(Repository)是存储和分发 Docker 镜像的地方。镜像仓库类似于代码仓库,Docker Hub 的命名来自 GitHub,Github 是我们常用的代码存储和分发的地方。同样 Docker Hub 是用来提供 Docker 镜像存储和分发的地方。 谈…...

[NOIP2009 提高组] 最优贸易(C++,tarjan,topo,DP)
题目描述 $C 国有国有国有 n 个大城市和个大城市和个大城市和 m$ 条道路,每条道路连接这 nnn个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这 mmm 条道路中有一部分为单向通行的道路,一部分为双向通行的道路,双向通行的…...

计算机网络:移动IP
移动IP相关概念 移动IP技术是移动结点(计算机/服务器)以固体的网络IP地址,实现跨越不同网段的漫游功能,并保证了基于网络IP的网络权限在漫游中不发生任何改变。移动结点:具有永久IP地址的设备。归属代理(本…...

binutils工具集——GNU binutils工具集简介
以下内容源于网络资源的学习与整理,如有侵权请告知删除。 GNU binutils是一个二进制工具集,主要包括: ld,GNU链接器。as,GNU汇编器。addr2line,把地址转化为文件名和行号。nm,列出目标文件的符…...
有趣应用)
Golang编译选项(ldflags)有趣应用
本文介绍如何在构建时使用ldflags选项给Golang应用程序注入变量,用于给Go可执行文件增加版本标识或GIT提交摘要等信息。 应用程序的版本信息 我们首先查看Docker Cli 包含的提交信息: docker version 返回结果: Server: Docker Engine - Co…...
 在AIR32F103上移植微雪墨水屏驱动)
AIR32F103(十一) 在AIR32F103上移植微雪墨水屏驱动
目录 AIR32F103(一) 合宙AIR32F103CBT6开发板上手报告AIR32F103(二) Linux环境和LibOpenCM3项目模板AIR32F103(三) Linux环境基于标准外设库的项目模板AIR32F103(四) 27倍频216MHz,CoreMark跑分测试AIR32F103(五) FreeRTOSv202112核心库的集成和示例代码AIR32F103(六) ADC,I2S…...

Uipath Excel 自动化基础系列文章
Uipath Excel 自动化基础系列文章已发布到CSDN,网址:https://blog.csdn.net/Marshaljun?typeblog (3月份会在CSDN博客发布Uipath Excel 实战课程及经验分享) Uipath Studio流程设计器介绍 https://blog.csdn.net/Marshaljun/article/details/128699022 Uipath St…...

神经网络优化器之随机梯度下降法的理解
随机梯度下降法(SGD)随机梯度下降方法,在每次更新时用1个样本,随机也就是说我们用样本中的一个例子来近似我所有的样本,由于计算得到的并不是准确的一个梯度,因而不是全局最优的。但是相比于批量梯度&#…...
记录一次WIN11开机在登录页面循环的问题
记录一次由于未进行win密码设置,导致开机后卡在登录界面无法登录进去的问题。最后完美解决了。 1. 背景 开机后,显示用户登录界面,但是和以往不同,没有了密码输入框,只有一个“登录”按钮孤零零地显示在屏幕中间&…...

始终从最不易改变的方面开始
在你刚开始新工作、转换职业或者是加入新项目时,始终从最不易改变的方面开始。 在工作中,这可能意味着与团队成员建立关系,了解公司的流程和文化,或者熟悉公司的产品或服务。 在一项新项目中,这可能意味着了解项目范…...

4、Httpclient源码解析之HTTP协议
初始化CloseableHttpClient过程中涉及ExecChainHandler & DefaultHttpProcessor,即典型客户端责任链中的请求执行处理器。 责任链中各节点涉及请求处理器【ExecChainHandler】顺序如下:RedirectExec、ContentCompressionExec、HttpRequestRetryExec…...
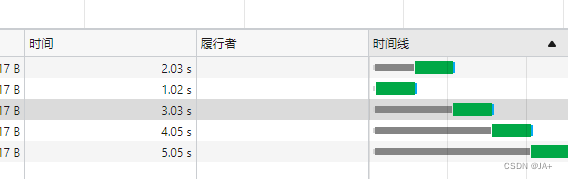
浏览器并发行为记录
使用nodejs koa起一个服务,使请求延时返回。 服务端代码 /** 延时 */ exports.timeoutTestData async function (ctx) {console.log(get query:, ctx.request.query);const query ctx.request.query;let timeout query.timeout || 2000;await new Promise(res…...

工厂模式与抽象工厂
原理:逻辑和业务全部封装 不需要细节 只要结果 示例: # 简单工厂 class SimpleFactory:# 产品staticmethoddef product(name):return nameif __name__ "__main__":product SimpleFactory.product("Gitee")print(product) 装饰器…...

什么?你不知道 ConcurrentHashMap 的 kv 不能为 null?
一、背景 最近设计某个类库时使用了 ConcurrentHashMap 最后遇到了 value 为 null 时报了空指针异常的坑。 本文想探讨下以下几个问题: (1) Map接口的常见子类的 kv 对 null 的支持情况。 (2)为什么 ConcurrentHashM…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...
