LeetCode——判断回文数
给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。
回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。
例如,121 是回文,而 123 不是。
示例 1:
输入:x = 121 输出:true
示例 2:
输入:x = -121 输出:false
解释:从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。
示例 3:
输入:x = 10 输出:false
解释:从右向左读, 为 01 。因此它不是一个回文数。
解答:
bool isPalindrome(int x) {long long int g = 0;long long int n = x;if(x < 0) return false;while(n > 0){g = n%10 + g*10;n = n/10;}if(x == g){return true;}else{return false;}}相关文章:

LeetCode——判断回文数
给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。 回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。 例如,121 是回文,而 …...
)
shell:使用结构化语句(for、while循环)
1. for命令 下面是bash shell中for命令的基本格式。 for var in list docommands done每次for命令遍历值列表,它都会将列表中的下个值赋给$test变量。$test变量可以像for 命令语句中的其他脚本变量一样使用。在最后一次迭代后,$test变量的值会在shell脚…...
数据结构_绪论
1.数据结构的研究内容 研究数据的特性和数据之间的关系 用计算机解决一个问题的步骤 1.具体问题抽象成数学模型 实质: 分析问题--->提取操作对象--->找出操作对象之间的关系(数据结构)--->用数学语言描述 操作对象对象之间的关系 2.设计算法 3.编程,调试,运行 …...

AI自动生成角色和情节连续的漫画,中山大学联想提出AutoStudio,可以多轮交互式连续生成并保持主题一致性。
中山大学和联想研究院提出AutoStudio: 是一种无需训练的多代理框架,用于多轮交互式图像生成,能够在生成多样化图像的同时保持主体一致性。 AutoStudio 采用三个基于 LLM 的智能体来解释人类意图并为 SD 模型生成适当的布局指导。此外,还引入…...

【经典面试题】RabbitMQ如何防止重复消费?
RabbitMQ的消息消费是有确认机制的,正常情况下,消费者在消费消息成功后,会发送一个确认消息,消息队列接收到之后,就会将该消息从消息队列中删除,下次也就不会再投递了。 但是如果存在网络延迟的问题&#…...

如何自己录制教学视频?零基础也能上手
随着在线教育的蓬勃发展,录制教学视频成为了教师和教育工作者们不可或缺的一项技能。无论是为了远程教学、课程分享还是知识普及,教学视频的录制都变得愈发重要。可是如何自己录制教学视频呢?本文将介绍两种录制教学视频的方法,这…...

【android】用 ExpandableListView 来实现 TreeView树形菜单视图
使用 ExpandableListView 来实现 TreeView 创建一个 ExpandableListAdapter 来为其提供数据。以下演示了如何使用 ExpandableListView 来展示树形结构的数据: 首先,在布局文件中添加 ExpandableListView: <ExpandableListViewandroid:i…...

策略模式与函数式编程应用
策略模式 | 单一职责原则(Single Responsibility Principle, SRP):islenone和islentwo分别根据特定条件返回电话号码 函数式编程: ‘’ if pd.isna(self.note1) else len(re.findall(r’\d, self.note1)) 重复代码: 当…...

docker原理记录C-N-A
docker原理 容器技术的兴起源于 PaaS 技术的普及 Docker 项目通过“容器镜像”,解决了应用打包这个根本性难题容器本身没有价值,有价值的是“容器编排”Cgroups 和 Namespace Cgroups 技术是用来制造约束的主要手段,而Namespace 技术则是用…...

【LeetCode】每日一题:二叉树的层次遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。 解题思路 水题 AC代码 # Definition for a binary tree node. # class TreeNode: # def __init__(self, val0, leftNone, rightN…...
单体架构改造为微服务架构之痛点解析
1.微服务职责划分之痛 1.1 痛点描述 微服务的难点在于无法对一些特定职责进行清晰划分,比如某个特定职责应该归属于服务A还是服务B? 1.2 为服务划分原则的痛点 1.2.1 根据存放主要数据的服务所在进行划分 比如一个能根据商品ID找出商品信息的接口,把…...

马面裙的故事:汉服如何通过直播电商实现产业跃迁
【潮汐商业评论/原创】 波澜壮阔的千里江山在马面裙的百褶上展开,织金花纹在女性的步伐之间若隐若现,从明清到现代,如今马面裙又流行了回来,成为女性的流行单品,2024年春节期间,马面裙更是成为华夏女孩们的…...

SaaS产品运营:维护四个不同类型的合作伙伴的实战指南
在SaaS(软件即服务)行业的竞争中,与合作伙伴建立并维护良好关系至关重要。不同类型的合作伙伴对于产品的推广、市场覆盖和用户增长都起着不同的作用。如何有效维护这四种类型合作伙伴?看个案例一起学习吧。 一、合作伙伴的四种类型…...

【监控】3.配置 Grafana 以使用 Prometheus 数据源
1 访问 Grafana 打开浏览器,访问 http://localhost:3000(默认端口)。使用默认的用户名和密码 admin/admin 登录。 2 添加 Prometheus 数据源 进入 Grafana 仪表板,点击左侧菜单中的“Configuration” -> “Data Sources”。…...

【LinuxC语言】网络编程中粘包问题
文章目录 前言什么叫做粘包问题粘包问题如何解决?总结前言 在进行网络编程时,我们经常会遇到一个非常常见但又往往被忽视的问题,那就是"粘包"问题。粘包是指在基于TCP/IP协议的数据传输过程中,由于TCP/IP协议是基于字节流的,这就可能会导致多个数据包被一起接收…...

Docker之jekins的安装
jekins官网地址:Jenkins Plugins (https://plugins.jenkins.io/) jekins 的docker 官方地址:https://hub.docker.com/r/jenkins/jenkins jekins 的docker 允许命令文档地址: docker/README.md at master jenkinsci…...

# bash: chkconfig: command not found 解决方法
bash: chkconfig: command not found 解决方法 一、chkconfig 错误描述: 这个错误表明在 Bash 环境下,尝试执行 chkconfig 命令,但是系统找不到这个命令。chkconfig 命令是一个用于管理 Linux 系统中服务的启动和停止的工具,通常…...

Linux线程互斥锁
目录 🚩看现象,说原因 🚩解决方案 🚩互斥锁 🚀关于互斥锁的理解 🚀关于原子性的理解 🚀如何理解加锁和解锁是原子的 🚩对互斥锁的简单封装 引言 大家有任何疑问,可…...

展开说说:Android列表之RecyclerView
RecyclerView 它是从Android5.0出现的全新列表组件,更加强大和灵活。用于显示列表形式 (list) 或者网格形式 (grid) 的数据,替代ListView和GridView成为Android主流的列表组件。可以说Android客户端只要有表格的地方就有RecyclerView。 RecyclerView 内…...

等保2.0时,最常见的挑战是什么?
等保2.0的常见挑战 等保2.0(网络安全等级保护2.0)是中国网络安全领域的基本制度,它对信息系统进行分级分类、安全保护和安全测评,以提高信息系统的安全性和可信性。在等保2.0的实施过程中,企业和组织面临多方面的挑战&…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...
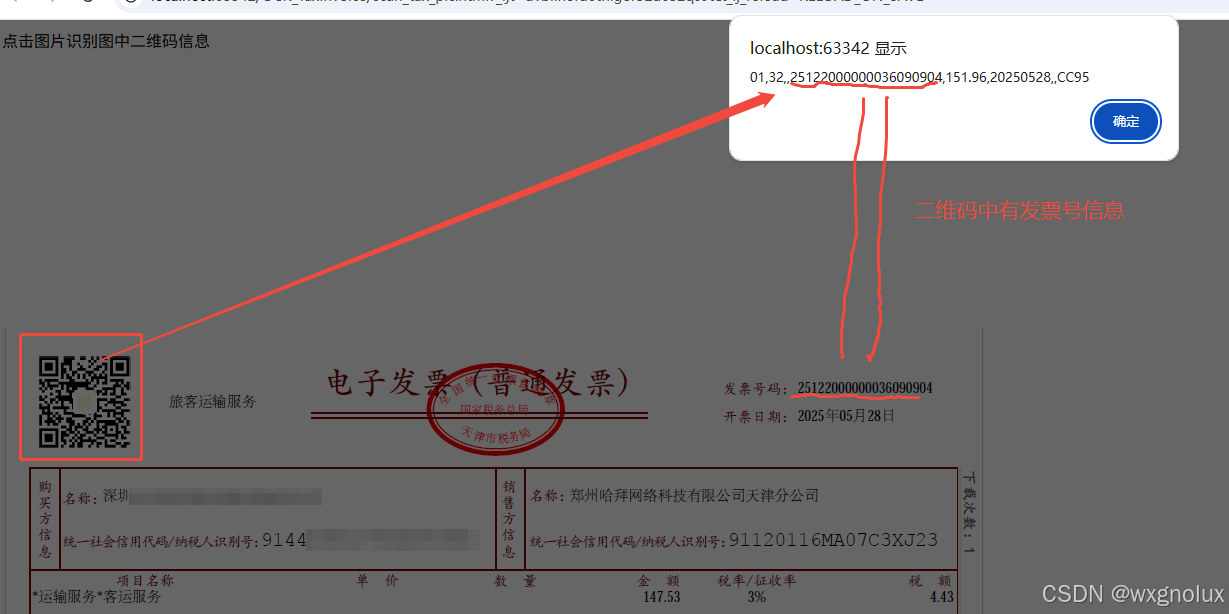
网页端 js 读取发票里的二维码信息(图片和PDF格式)
起因 为了实现在报销流程中,发票不能重用的限制,发票上传后,希望能读出发票号,并记录发票号已用,下次不再可用于报销。 基于上面的需求,研究了OCR 的方式和读PDF的方式,实际是可行的ÿ…...

【2D与3D SLAM中的扫描匹配算法全面解析】
引言 扫描匹配(Scan Matching)是同步定位与地图构建(SLAM)系统中的核心组件,它通过对齐连续的传感器观测数据来估计机器人的运动。本文将深入探讨2D和3D SLAM中的各种扫描匹配算法,包括数学原理、实现细节以及实际应用中的性能对比,特别关注…...
