ABC355 Bingo2
分析:
找出其中一行或列或任意对角线被全部标记,即可输出回合数,否则输出-1
如果x%n=0,行是x/n,列是n
如果x%n!=0,行是x/n+1,列是x%n
如果行=列或行+列=n+1即为对角线。
标记行列对角线,当其中一行或列或任意对角线被全部标记,即输出。
#include<bits/stdc++.h>
using namespace std;
const int N=2e3+10;
int hang[N]={0},lie[N]={0};
//xx为撇 xxx为捺
int main() {
int n,t,c,xx=0,xxx=0,x;cin>>n>>t;int f=-1;
for(int i=1;i<=t;i++){
cin>>x;
if(x%n==0){
hang[x/n]++;
lie[n]++;
if(x/n==n)xxx++;
if(x/n==1)xx++;
if((hang[x/n]==n||lie[n]==n||xx==n||xxx==n)&&f==-1)f=i;
}
else{
hang[x/n+1]++;
lie[x%n]++;
if(x/n+1==x%n)xxx++;
if(x/n+1+x%n==n+1)xx++;
if((hang[x/n+1]==n||lie[x%n]==n||xx==n||xxx==n)&&f==-1)f=i;
}
}
cout<<f<<endl;
return 0;
}
相关文章:

ABC355 Bingo2
分析: 找出其中一行或列或任意对角线被全部标记,即可输出回合数,否则输出-1 如果x%n0,行是x/n,列是n 如果x%n!0,行是x/n1,列是x%n 如果行列或行列n1即为对角线。 标记行列对角线…...
Spring+Vue项目部署
目录 一、需要的资源 二、步骤 1.首先要拥有一个服务器 2.项目准备 vue: 打包: 3.服务器装环境 文件上传 设置application.yml覆盖 添加启动和停止脚本 编辑 安装jdk1.8 安装nginx 安装mysql 报错:「ERR」1273-Unknown collation: utf8m…...
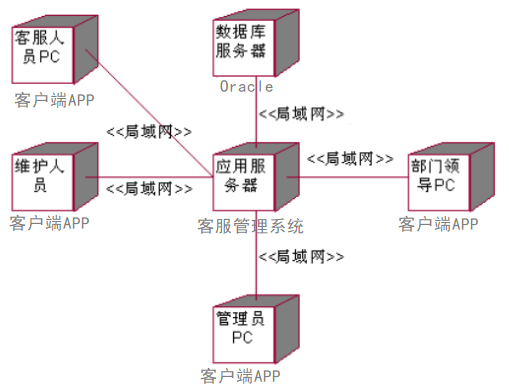
【uml期末复习】统一建模语言大纲
前言: 关于uml的期末复习的常考知识点,可能对你们有帮助😉 目录 第一部分 概念与基础 第一章 面向对象技术 第二章 统一软件过程 第三章 UML概述 第四章 用例图 第五章 类图 第六章 对象图 第七章 顺序图 第八章 协作图 第九章 状态…...
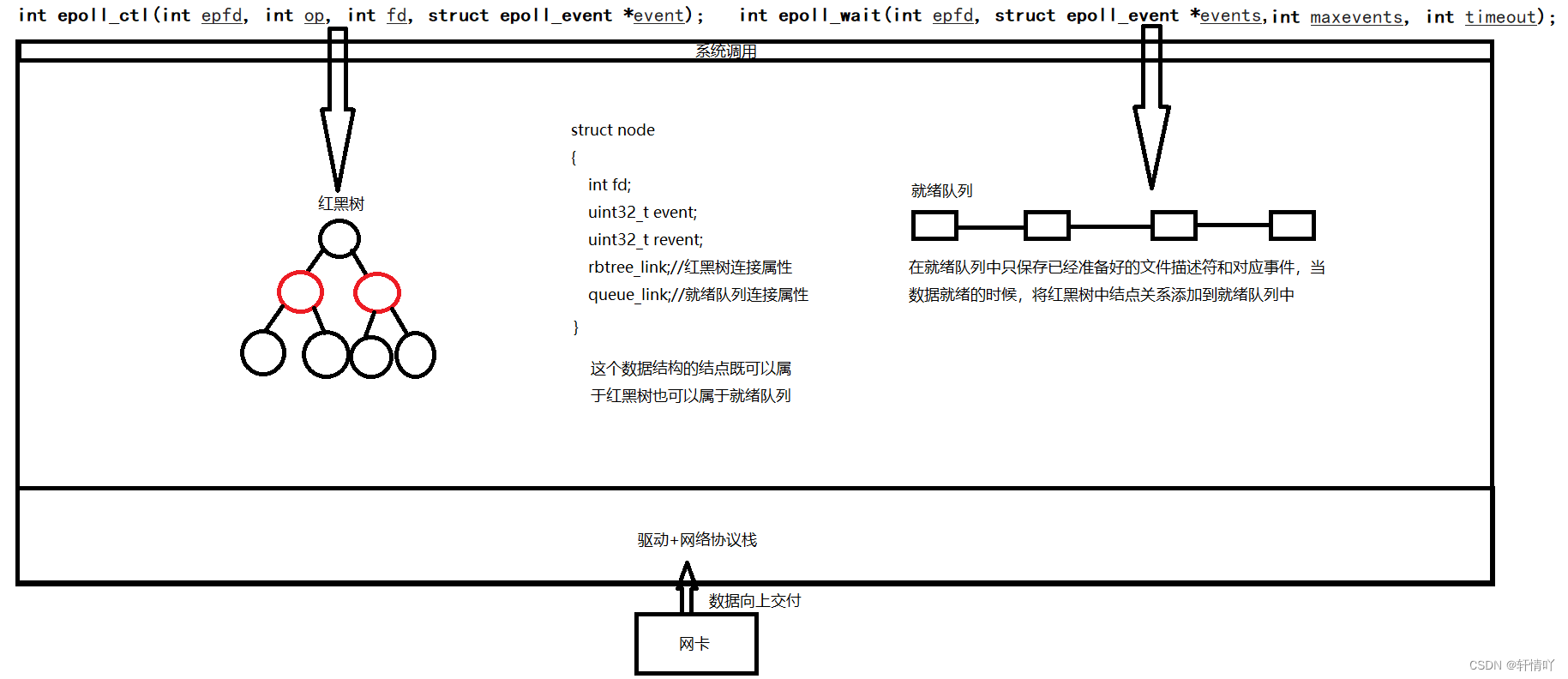
Linux高级IO
高级IO 1.五种IO模型1.1 阻塞IO1.2 非阻塞IO1.3 信号驱动IO1.4 多路复用/多路转接IO1.5 异步IO1.6 小结 2.高级IO重要概念3.非阻塞IO3.1 实现函数NoBlock3.2 轮询方式读取标准输入 4.I/O多路转接之select4.1 理解select执行过程4.2 select的特点4.3 select缺点4.4 实现 5.I/O多…...
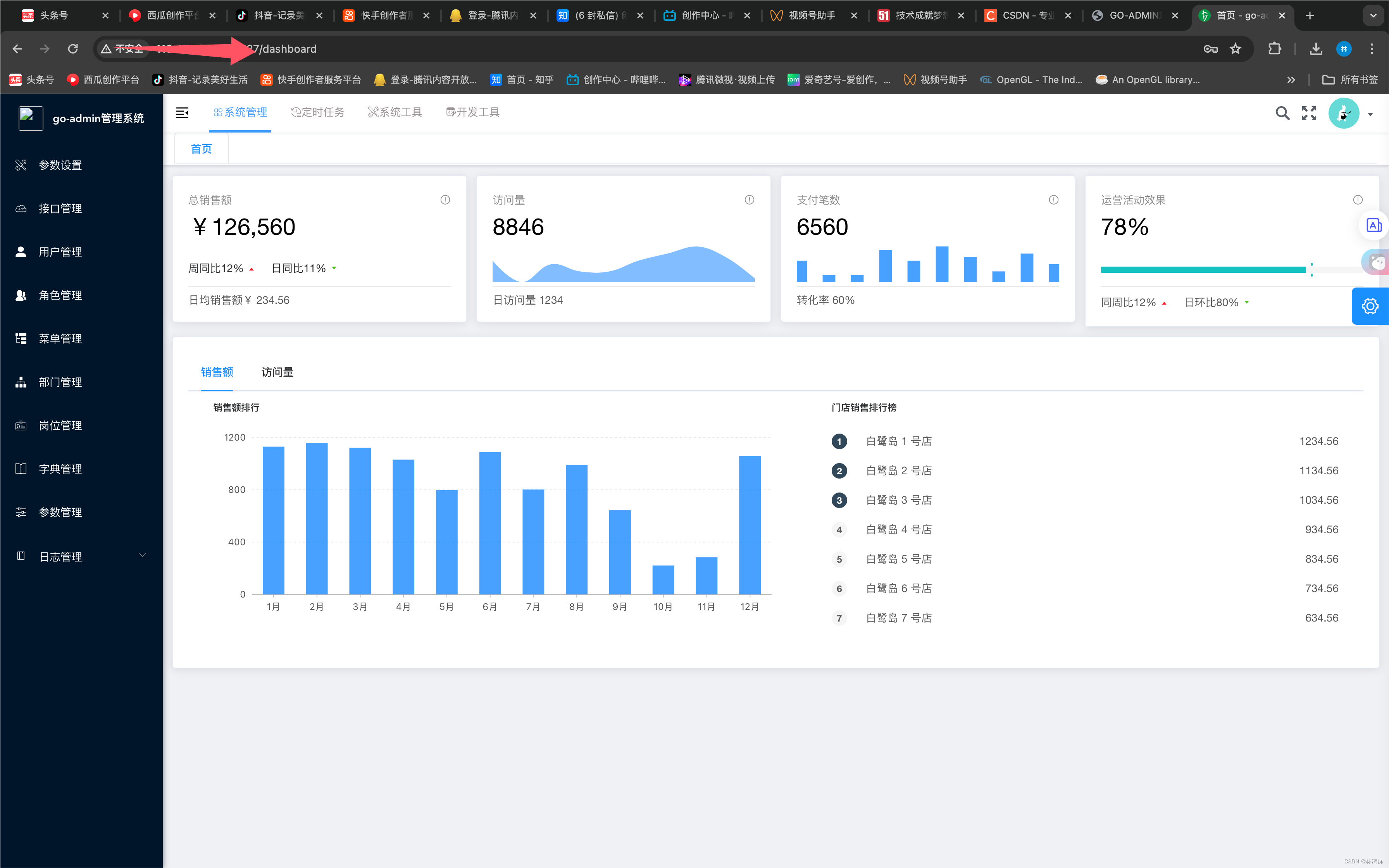
go-admin-ui开源后台管理系统华为云部署
1.华为云开通8000与9527端口 2.编译 编译成功 3.发布到远程服务器 4.登陆华为云终端 5.安装Nginx 6.查看服务启动状态 7.添加网站 添加与修改配置www-data 改为 www 自定义日志输出格式 添加网站配置文件go_admin_ui.conf 添加如下内容: location 下的root指向网站文件夹 修…...

点云入门知识
点云的处理任务 场景语义分割 物体的三维表达方法(3D representations): 点云:是由物体表面上许多点数据来表征这个物体。最接近原始传感器数据,且具有丰富的几何信息。 Mesh:用三角形面片和正方形面片拼…...

HTML静态网页成品作业(HTML+CSS+JS)——家乡莆田介绍网页(5个页面)
🎉不定期分享源码,关注不丢失哦 文章目录 一、作品介绍二、作品演示三、代码目录四、网站代码HTML部分代码 五、源码获取 一、作品介绍 🏷️本套采用HTMLCSS,使用Javacsript代码实现图片轮播,共有5个页面。 二、作品…...

#### grpc比http性能高的原因 ####
grpc比http性能高的原因 二进制消息格式:gRPC使用Protobuf(一种有效的二进制消息格式)进行序列化,这种格式在服务器和客户端上的序列化速度非常快,且序列化后的消息体积小,适合带宽有限的场景。 HTTP/2协…...

微软Edge浏览器搜索引擎切换全攻略
微软Edge浏览器作为Windows 10的默认浏览器,提供了丰富的功能和良好的用户体验。其中,搜索引擎的切换功能允许用户根据个人喜好和需求,快速更换搜索引擎,从而获得更加个性化的搜索服务。本文将详细介绍如何在Edge浏览器中进行搜索…...

<Linux> 实现命名管道多进程任务派发
实现命名管道多进程任务派发 common文件 #ifndef _COMMON_H_ #define _COMMON_H_#pragma once #include <iostream> #include <unistd.h> #include <string> #include <sys/types.h> #include <sys/stat.h> #include <wait.h> #include &…...

BigInteger 和 BigDecimal(java)
文章目录 BigInteger(大整数)常用构造方法常用方法 BigDecimal(大浮点数)常用构造方法常用方法 DecimalFormat(数字格式化) BigInteger(大整数) java.math.BigInteger。 父类:Number 常用构造方法 构造方法:BigIntege…...

Linux 进程间通讯
Linux IPC 方式 在Linux系统中,进程间通信(IPC)是多个运行中的程序或进程之间交换数据和信息的关键机制。Linux提供了多种IPC机制,每种机制都有其特定的用途和优势。以下是Linux上主要的IPC通信方式: 管道(…...

数据分析三剑客-Matplotlib
数据分析三剑客 数据分析三剑客通常指的是在Python数据分析领域中,三个非常重要的工具和库:Pandas、NumPy和Matplotlib。Pandas主要负责数据处理和分析,NumPy专注于数值计算和数学运算,而Matplotlib则负责数据可视化。这三个库相…...

FastAPI-Body、Field
参考:模式的额外信息 - 例子 - FastAPI 在FastAPI中,Body和Field是两个常用的注解,它们用于定义请求体中的数据或路径参数、查询参数等的处理方式。这两个注解都来自于Pydantic库,用于数据验证和解析,但它们的应用场景…...
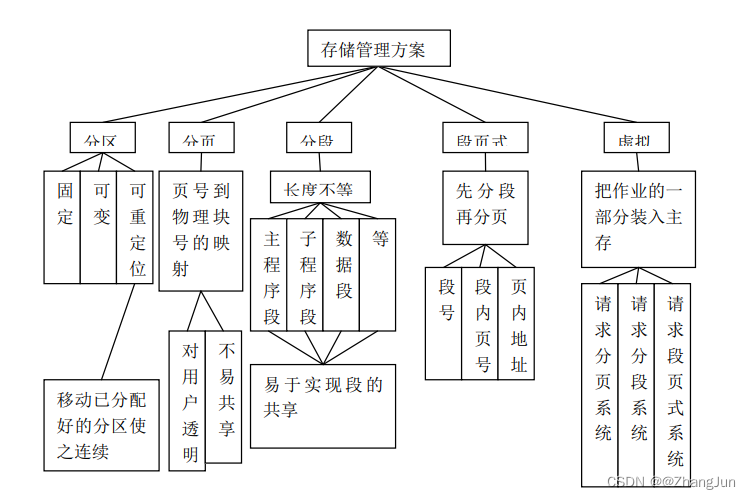
软件设计师笔记-操作系统知识(二)
线程 以下是关于线程的一些关键点: 线程是进程中的一个实体:进程是操作系统分配资源(如内存空间、文件句柄等)的基本单位,而线程是进程中的一个执行单元。多个线程可以共享同一个进程的地址空间和其他资源。线程是CP…...

鸿蒙UI开发快速入门 —— part12: 渲染控制
如果你对鸿蒙开发感兴趣,加入Harmony自习室吧~👇🏻👇🏻👇🏻👇🏻 扫描下面的二维码关注公众号。 1、前言 在声明式描述语句中开发者除了使用系统组件外,还可…...
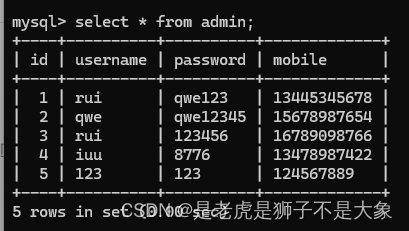
添加用户页面(Flask+前端+MySQL整合)
首先导入Flask库和pymysql库。Flask用于创建Web应用程序,pymysql用于连接和操作MySQL数据库。 from flask import Flask, render_template, request import pymysql创建一个Flask应用实例。__name__参数告诉Flask使用当前模块作为应用的名称。 app Flask(__name_…...
)
素数筛(算法篇)
算法之素数筛 素数筛 引言: 素数(质数):除了1和自己本身之外,没有任何因子的数叫做素数(质数) 朴素筛法(优化版) 概念: 朴素筛法:是直接暴力枚举2到当前判断的数x(不包括),然后看在这范围内是否存在因…...

迁移Microsoft Edge
如何将Microsoft Edge迁移到d盘?对于Microsoft Edge想必大部分人都不陌生,它是Windows操作系统的默认浏览器,存储用户的个人数据、缓存和设置等信息。有些时候,我们需要对Microsoft Edge中的数据进行数据迁移,以释放c盘…...
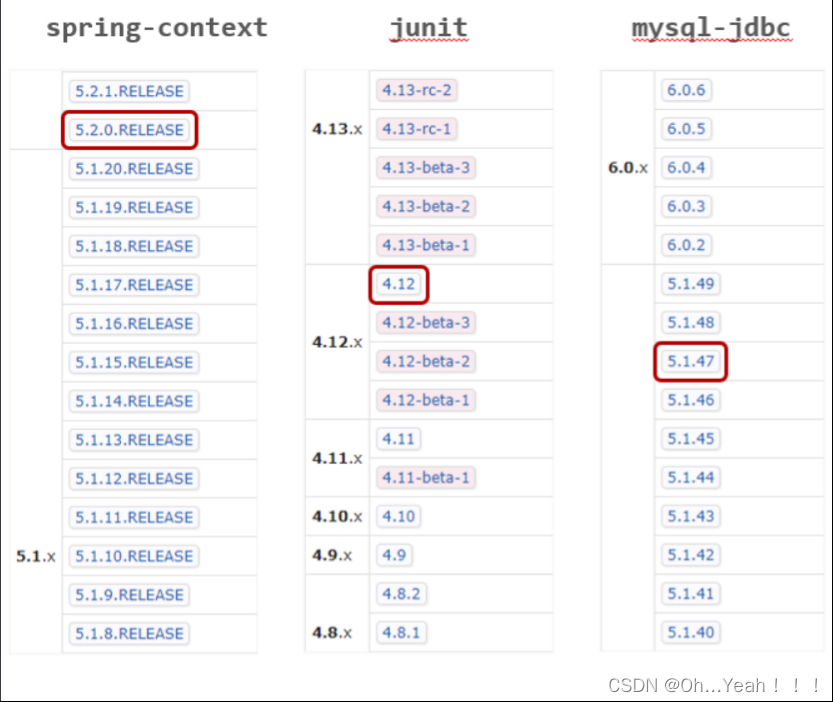
Maven高级理解属性
属性 在这一章节内容中,我们将学习两个内容,分别是 属性版本管理 属性中会继续解决分模块开发项目存在的问题,版本管理主要是认识下当前主流的版本定义方式。 4.1 属性 4.1.1 问题分析 讲解内容之前,我们还是先来分析问题: …...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

数据结构:泰勒展开式:霍纳法则(Horner‘s Rule)
目录 🔍 若用递归计算每一项,会发生什么? Horners Rule(霍纳法则) 第一步:我们从最原始的泰勒公式出发 第二步:从形式上重新观察展开式 🌟 第三步:引出霍纳法则&…...
