【数据结构之二叉树】——二叉树的概念及结构,特殊的二叉树和二叉树性质
文章目录
- 一、二叉树的概念及结构
- 1.概念
- 2.现实中的二叉树
- 3. 特殊的二叉树:
- 3.二叉树的性质
- 二、二叉树练习题
- 总结
一、二叉树的概念及结构
1.概念
一棵二叉树是结点的一个有限集合,该集合:
- 或者为空
- 由一个根节点加上两棵别称为左子树和右子树的二叉树组成
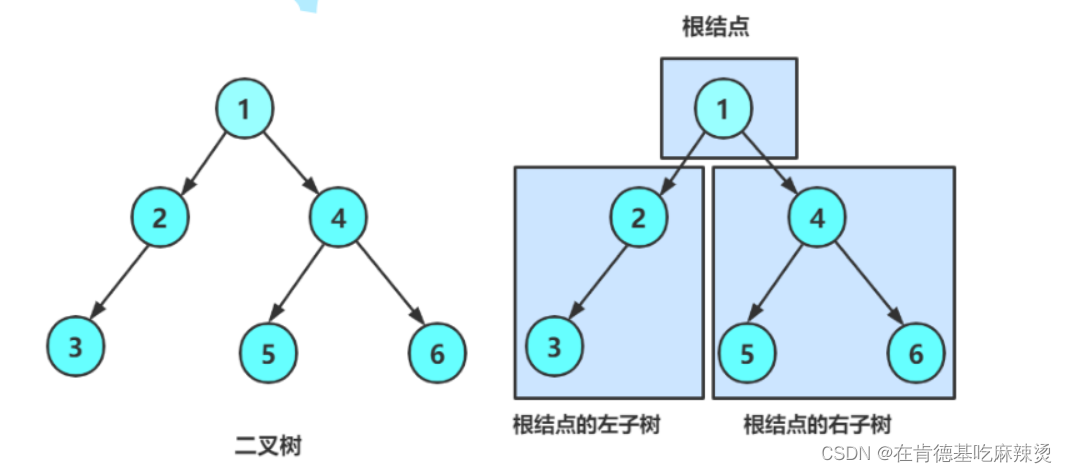
如上图就是二叉树,可以看出:
1.二叉树每个节点的度<=2
2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
注意:对于任意的二叉树都是由以下几种情况复合而成的:
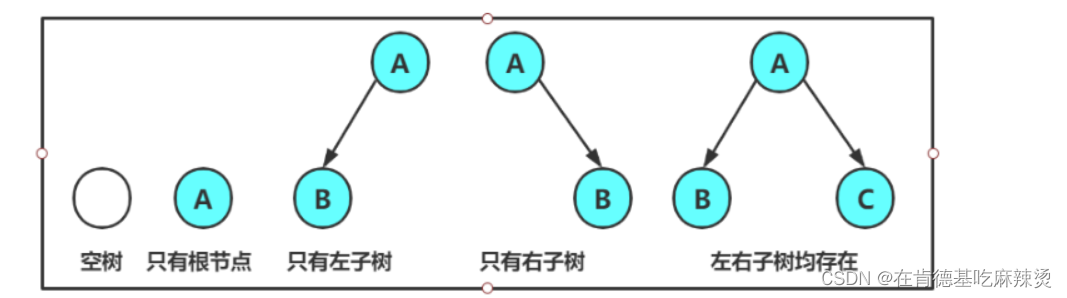
2.现实中的二叉树

3. 特殊的二叉树:
1)满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是2^K-1 ,则它就是满二叉树。
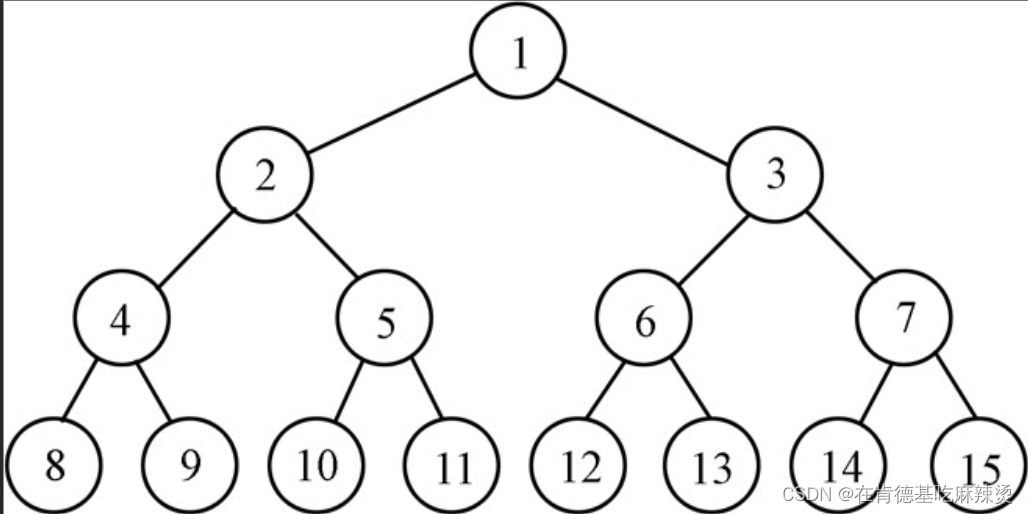
如上图:这是一棵满二叉树:
推导:
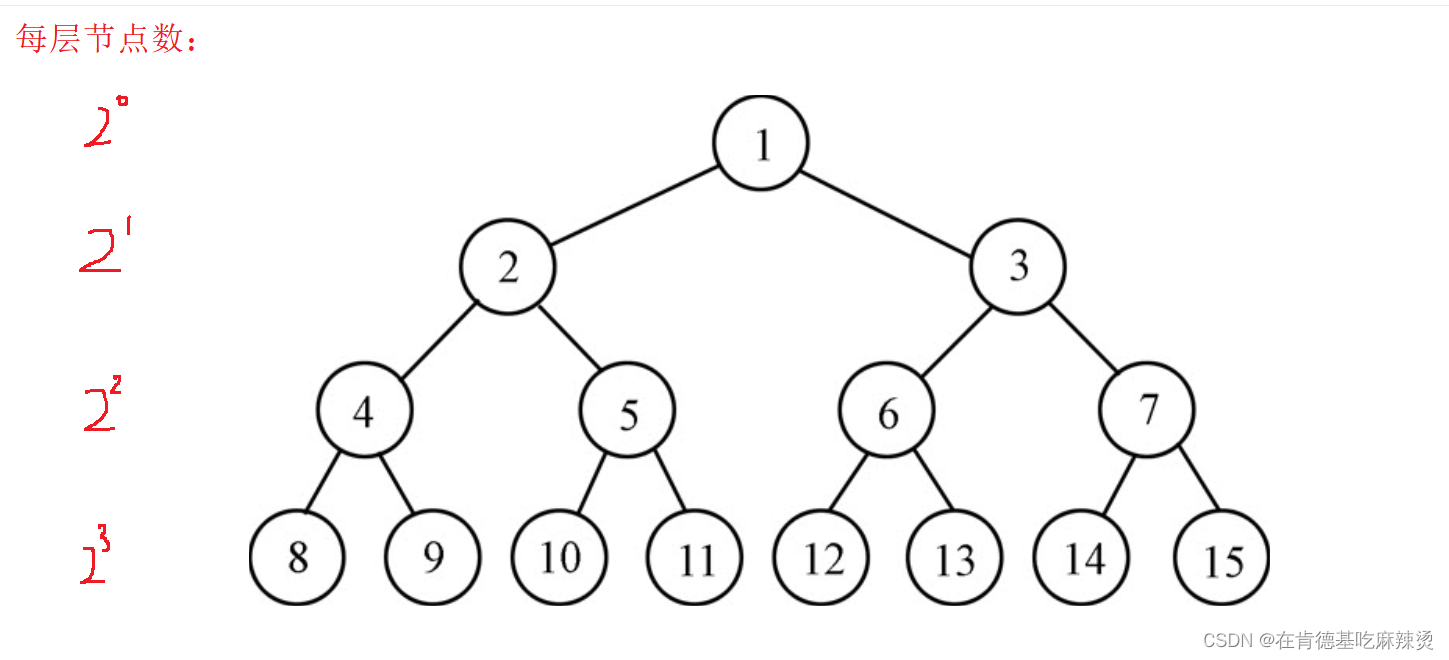
该二叉树的高度是h = 4.
则该二叉树的节点总数Sn = 2^0 + 2^1 + 2^2 + …+2^h-1
由等比数列求前n项和公式:

带入数据:
有 Sn = 2^h -1 (Sn为二叉树节点总数,h为树的高度)
所以这就是一棵标准的满二叉树。
如果我们知道一棵满二叉树的总节点个数,也可以推导出改满二叉树的节点的高度
推导如下:

h = log2(Sn+1)
2)完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
通俗地讲:
1)前面每层节点的度都是2
2)最后一层节点必须连续
要注意的是满二叉树是一种特殊的完全二叉树。
比如说下面这个:
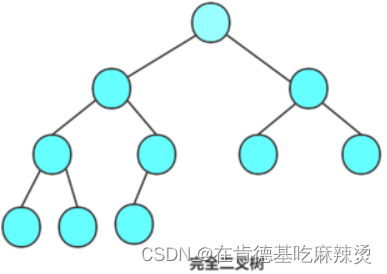
解释如下:
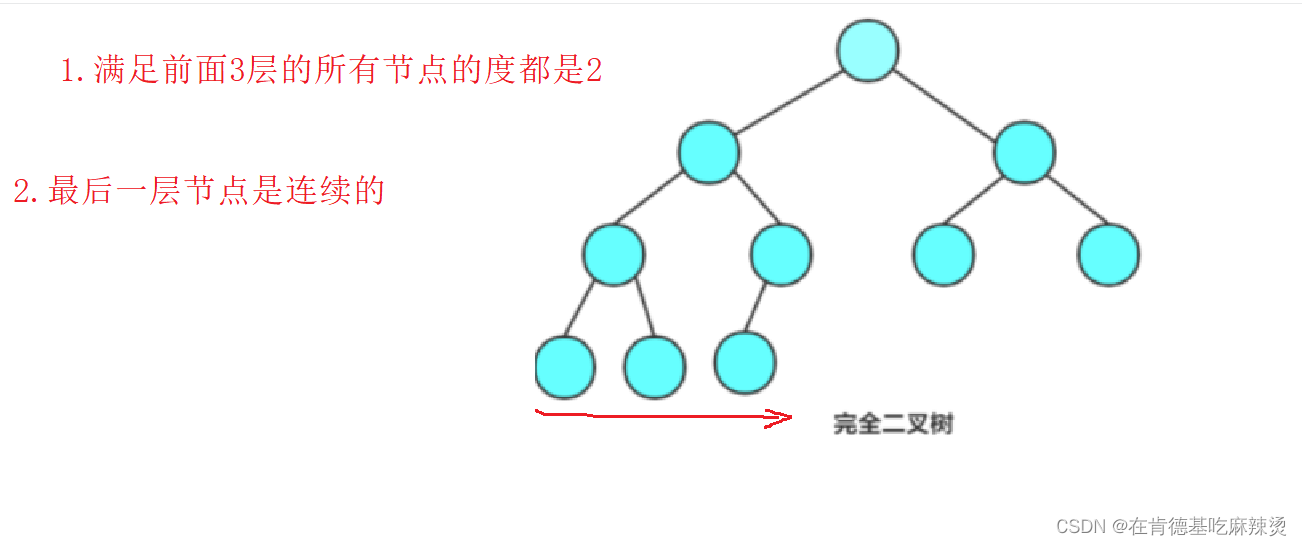
如果是这几种情况,就不是完全二叉树:
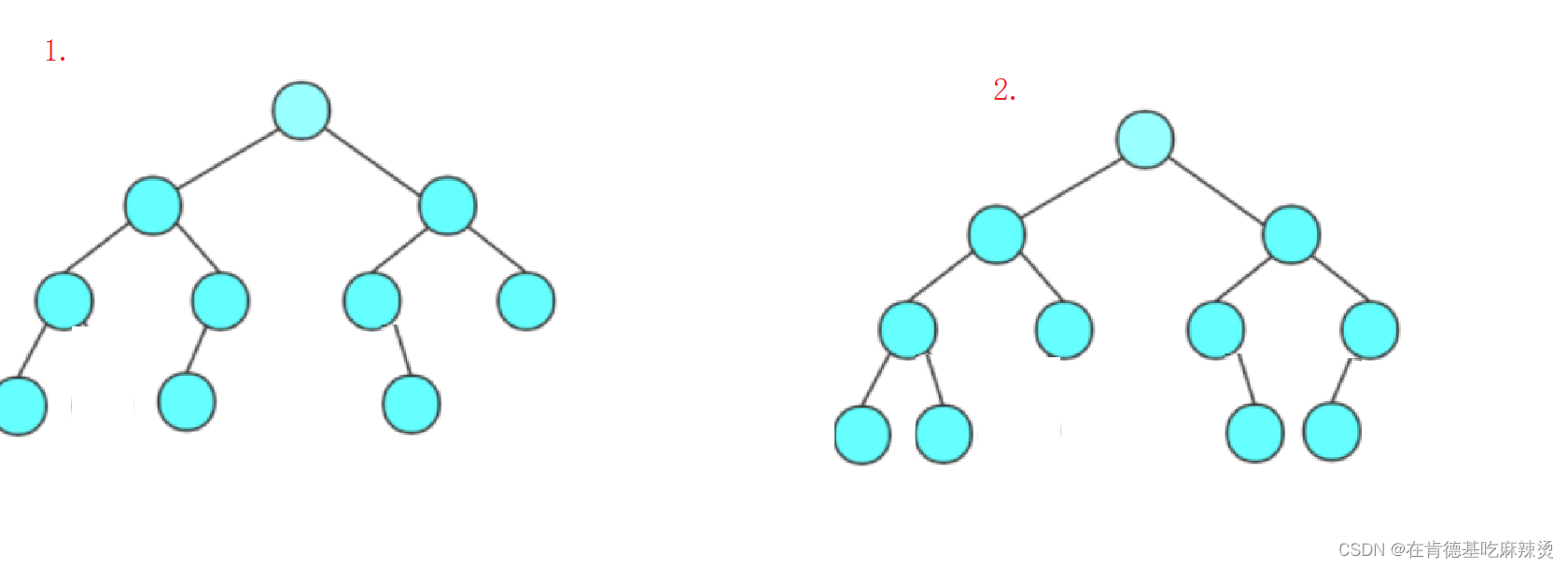
因为它们不符合第二点要求:最后一层是连续的。
由满二叉树和二叉树的定义可知,满二叉数是特殊的完全二叉树。
类似地:当我们知道完全二叉树的节点数,可以推导完全二叉树的高度:
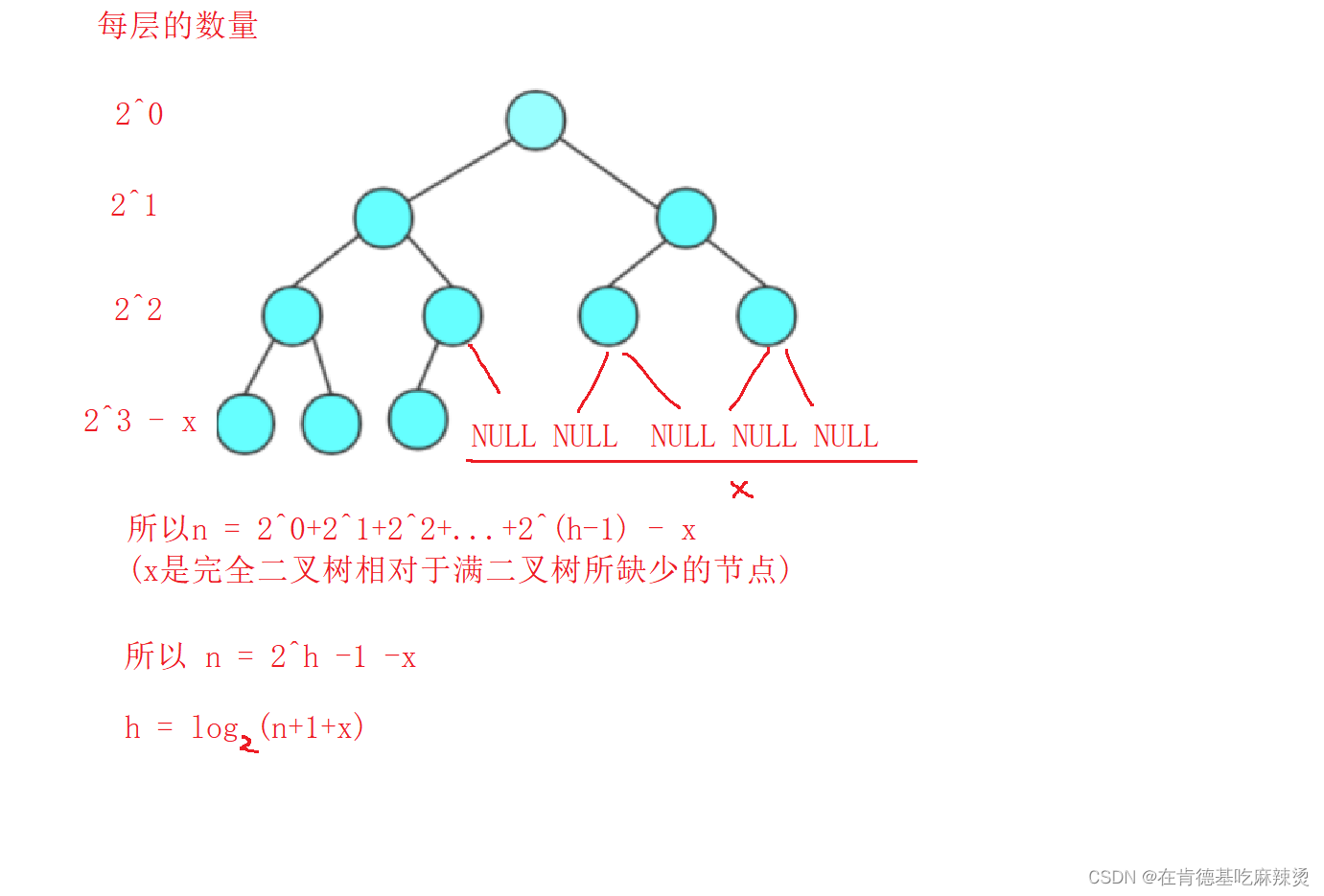
3.二叉树的性质
1. 若规定根节点的层数为1,则一棵非空二叉树的第n层上最多有2^(n-1) 个结点.
2. 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h - 1 .
3. 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h= log2(n+1). (ps: 是log以2为底,n+1为对数)
4. 对任何一棵二叉树, 如果度为0其叶结点个数为n0, 度为2的分支结点个数为n2 ,则有 n0= n2+1
第四点解析:
以下图为例,度为0的节点的个数有4个,度为2的节点的个数有3个,则n0 = n2 + 1
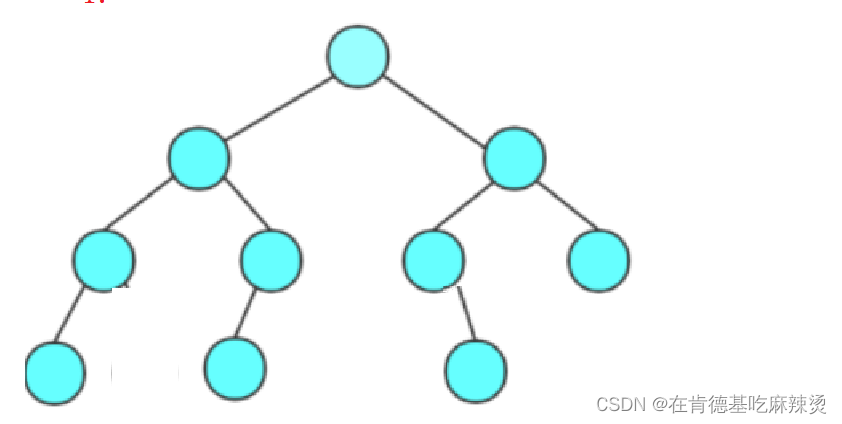
5. 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对
于序号为i的结点有:
1)若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
2)若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
3) 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
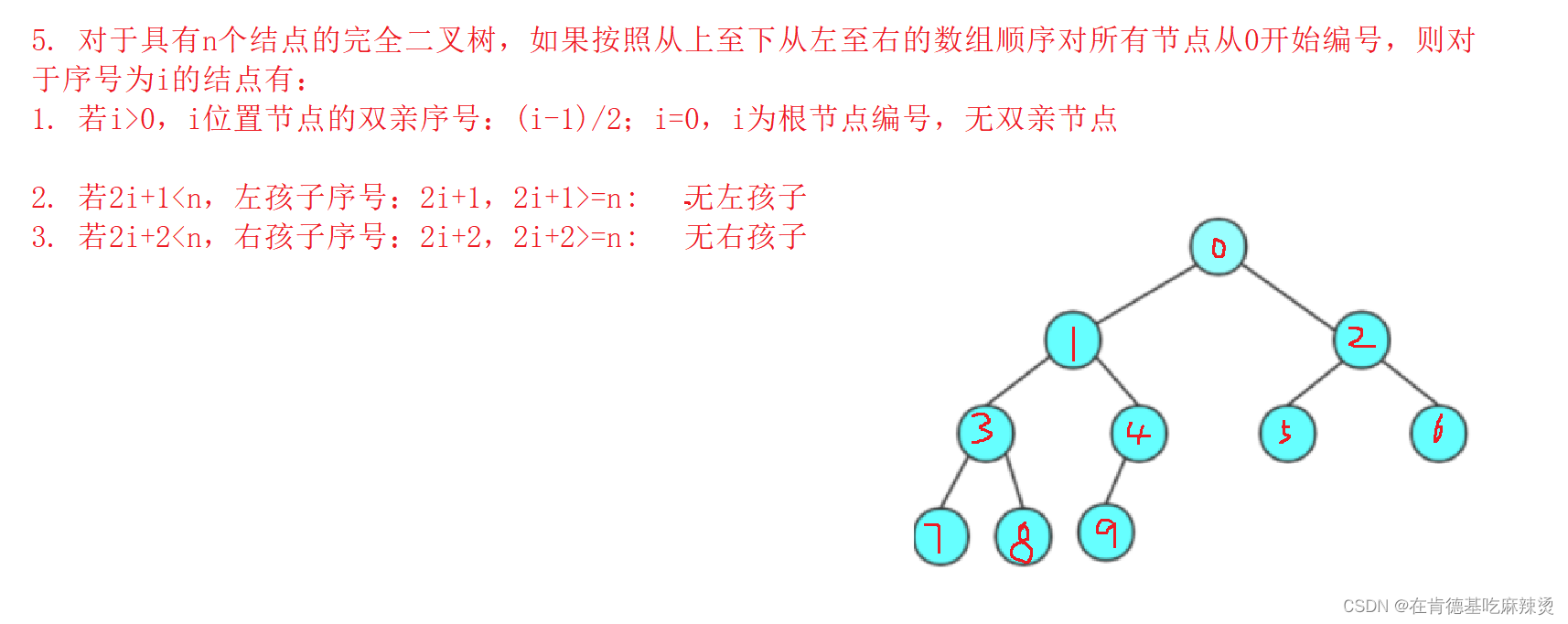
以该例子为例套进去即可。
前面三点是上面推导过的,第四点和第五点是重点要记忆的
二、二叉树练习题
1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( )
A 不存在这样的二叉树
B 200
C 198
D 199
解析:
运用上面所讲的性质四即可秒杀。
4. 对任何一棵二叉树, 如果度为0其叶结点个数为n0, 度为2的分支结点个数为n2 ,则有 n0= n2+1度为2的节点有199个,即n2 = 199,那么度为n0的节点 = n2+1 = 200
2.在具有 2n 个结点的完全二叉树中,叶子结点个数为( )
A n
B n+1
C n-1
D n/2
解析:
假设这棵完全二叉树的度为0,1,2的节点个数分别为:
x0 ,x1,x2
有: x0+x1+x2 = 2n
又根据性质四,x0 = x2 + 1,所以化简一下得:
x2+1+x1+x2 = 2n
对于一棵完全二叉树来说,度为1的节点的个数要么为0,要么为1
以上面这棵完全二叉树为例,度为1的节点只有1个
以上面这棵完全二叉树的节点为例:度为1的节点有0个。
所以对于任何一颗完全二叉树来说,度为1的节点只有1个或0个。
则x1 = 1或x1 = 0
当x1 = 1时,
x2+1+x1+x2 = 2n -->2*x2 + 2 = 2n,
所以x2 = n而当x1 = 0时,2*x2+1 = 2n,x2 = (2n-1)/2,节点个数不可能为小数,所以不成立
所以该完全二叉树的度为1的节点个数为n
3.一棵完全二叉树的节点数位为531个,那么这棵树的高度为( )
A 11
B 10
C 8
D 12
解析:
以这棵二叉树为例:
对于一棵完全二叉树,节点个数与高度的关系有:
n = 2^h-1-x(x为完全二叉树最后一层中缺少的节点的个数)
缺少的节点是相对于满二叉树来说的。
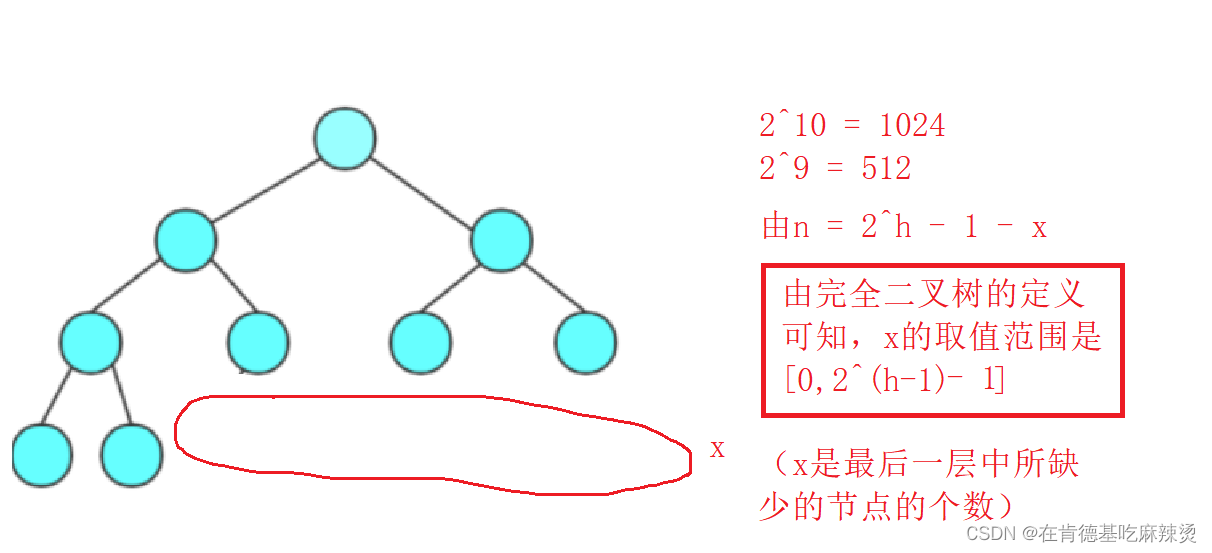
x的最好情况和最坏情况如下:
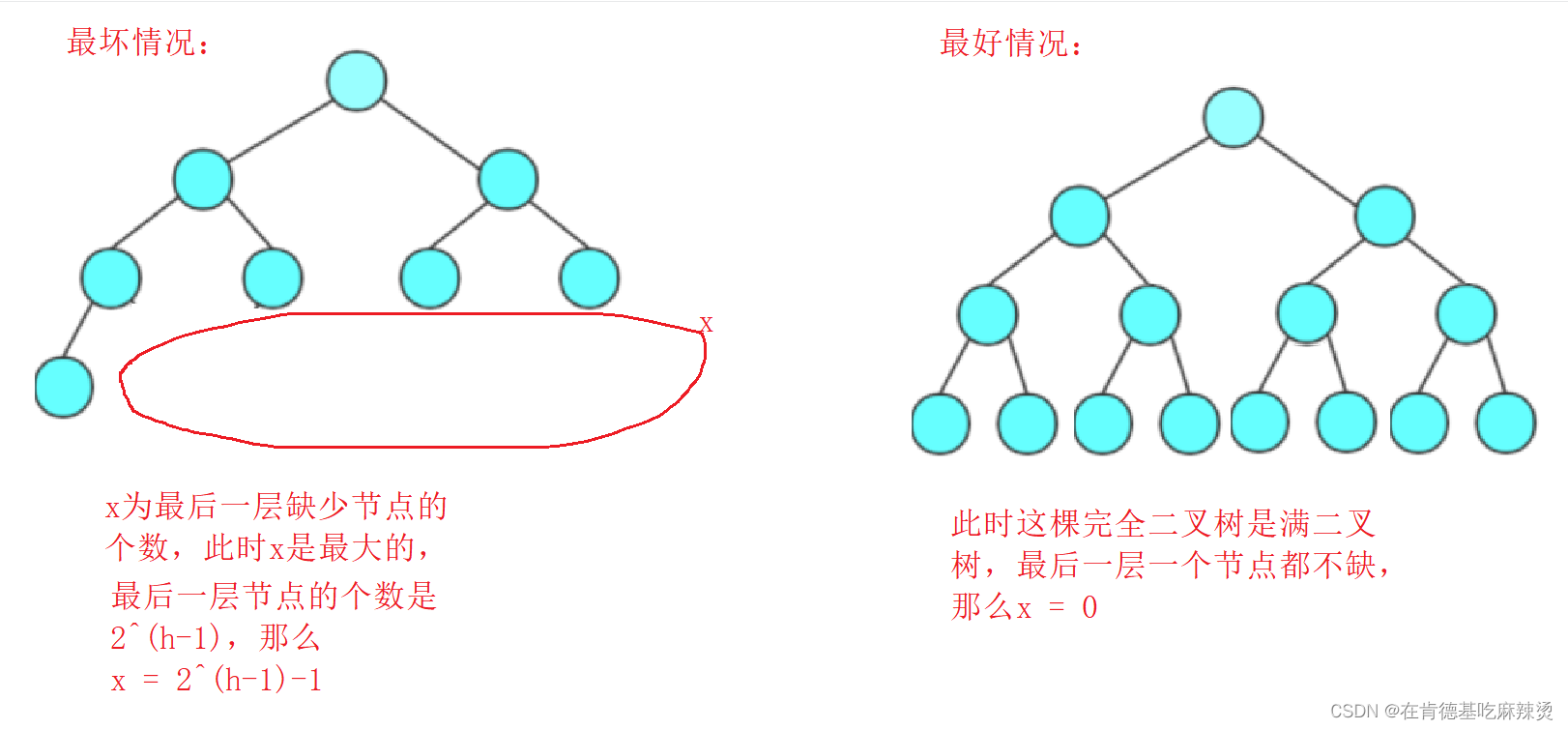
当h = 10时,节点个数为 2^10 - 1 - x ,
此时x的取值范围是[0,2^9-1-1],即[0,510]
代入原数据 531 = 2^10 -1 -x,x = 492,在取值范围内。当n = 11时,节点个数为2^11 -1 -x,
此时x的取值范围是[0,2^10-1-1],即[0,1022]
代入原数据 531 = 2^11 -1 -x,x = 1516,不在取值范围内,不成立。
而对于当h = 12时,更不可能了。
对与h = 8,2^8 = 256,也不可能
所以h = 10,选B
4.一个具有767个节点的完全二叉树,其叶子节点个数为()
A 383
B 384
C 385
D 386
解析:
这道题的解法与第2题解法相同
直接画图分析:
总结
熟知二叉树的相关知识概念和性质,非常有助于进一步二叉树广度优先搜索和深度优先搜索的学习。
相关文章:

【数据结构之二叉树】——二叉树的概念及结构,特殊的二叉树和二叉树性质
文章目录一、二叉树的概念及结构1.概念2.现实中的二叉树3. 特殊的二叉树:3.二叉树的性质二、二叉树练习题总结一、二叉树的概念及结构 1.概念 一棵二叉树是结点的一个有限集合,该集合: 或者为空由一个根节点加上两棵别称为左子树和右子树的二叉树组成…...

Android学习之帧动画和视图动画
帧动画 帧动画中的每一帧其实都是一张图片,将许多图片连起来播放,就形成了帧动画。 在drawable目录下新建frmae_animation文件,在这个文件中定义了帧动画的每一帧要显示的图片,播放时,按从上到下显示。 <?xml v…...

vue2和vue3的区别
这周呢主要就是整理整理学的东西,不然看的也记不住,把这些学的东西做成笔记,感觉会清楚许多,这次就把vue2和vue3的区别总结一下,明天要考四级,嗐,本来想着复习四级,结果只写了一两套…...
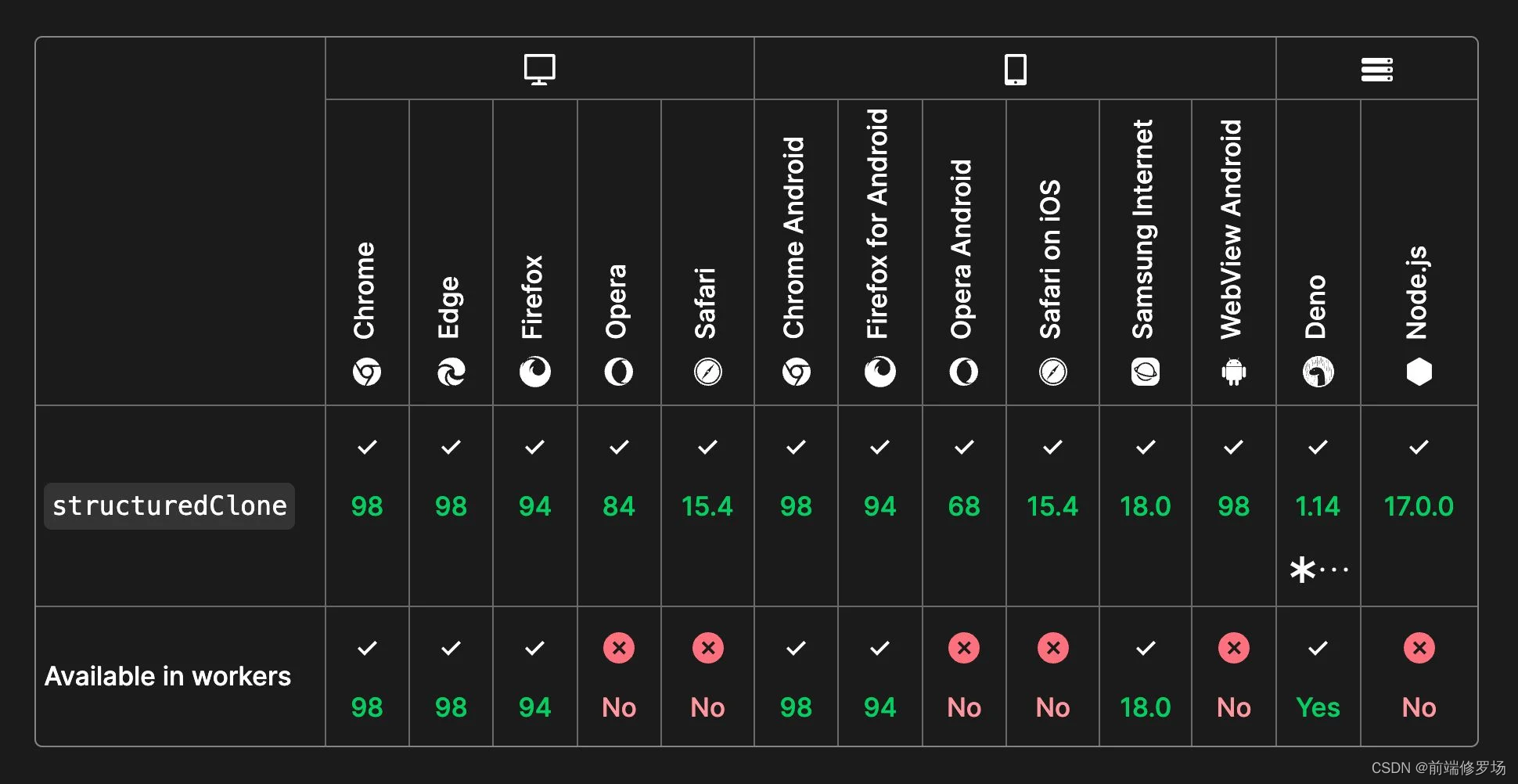
【你不知道的事】JavaScript 中用一种更先进的方式进行深拷贝:structuredClone
你是否知道,JavaScript中有一种原生的方法来做对象的深拷贝? 本文我们要介绍的是 structuredClone 函数,它是内置在 JavaScript 运行时中的: const calendarEvent {title: "Builder.io Conf",date: new Date(123),attendees: ["Steve…...
XE开发Linux应用(二)-Webservice
新建一个工程。选择如图。继续输入服务名然后就生成对应的单元。增加linux 平台。完善对应的单元代码{ Invokable implementation File for Txaliontest which implements Ixaliontest }unit xaliontestImpl;interfaceuses Soap.InvokeRegistry, System.Types, Soap.XSBuiltIns…...

kubernetes实战与源码学习
1.1 关于Kubernetes的介绍与核心对象概念 关于Kubernetes的介绍与核心对象概念-阿里云开发者社区 k8s架构 核心对象 使用kubeadm10分钟部署k8集群 使用 KuboardSpray 安装kubernetes_v1.23.1 | Kuboard k8s-上部署第一个应用程序 Deployment基本概念 给应用添加service&a…...

CNCF x Alibaba云原生技术公开课 第八章 应用配置管理
Pod配置管理分类 可变配置就用 ConfigMap;敏感信息是用 Secret;身份认证是用 ServiceAccount;资源配置是用 Resources;安全管控是用 SecurityContext;前置校验是用 InitContainers。 1、ConfigMap 概念:…...

YUV实践记录
文章目录YUV基础介绍:不同采样YUV格式的区别为什么要使用YUV格式呢?YUV的存储方式Android中的YUV_420_888附录:YUV基础介绍: YUV在做手机图像或者视频处理的时候会经常用到的一个格式,用此文来记录YUV相关介绍…...

【题解】百度2020校招Web前端工程师笔试卷(第一批):单选题、多选题
题目来源 若有错误请指正! 单选 1 分页存储管理将进程的逻辑地址空间分成若干个页,并为各页加以编号,从0开始,若某一计算机主存按字节编址,逻辑地址和物理地址都是32位,页表项大小为4字节,若…...
)
探索云原生技术之容器编排引擎-kubeadm安装kubernetes1.21.10(新版:针对高版本内核)
❤️作者简介:2022新星计划第三季云原生与云计算赛道Top5🏅、华为云享专家🏅、云原生领域潜力新星🏅 💛博客首页:C站个人主页🌞 💗作者目的:如有错误请指正,将…...

2023广西自治区职业技能大赛“网络安全” 项目比赛任务书
2023广西自治区职业技能大赛“网络安全” 项目比赛任务书2023广西自治区职业技能大赛“网络安全” 项目比赛任务书A模块基础设施设置/安全加固(200分)A-1:登录安全加固(Windows, Linux)A-2:Nginx安全策略&a…...
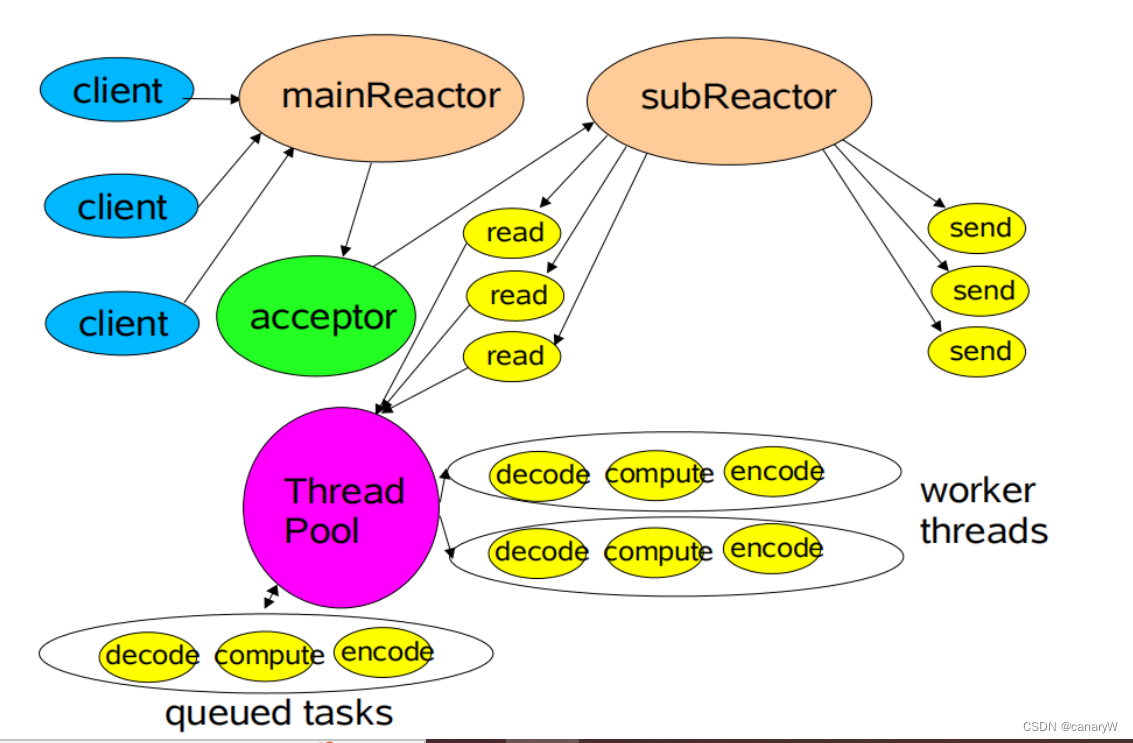
Reactor模式
Reactor是一种设计模式,可以用于构建高并发的网络服务器。 Reactor模式的好处在于:可以在一个或多个reactor线程使用多路复用技术去管理所有网络连接连接建立、IO请求,保证工作线程不被IO阻塞。 前置知识:IO多路复用技术 1. 传统网…...

Git图解-IDEA中的Git操作
目录 一、配置Idea 二、项目克隆 三、文件状态识别 四、Git操作 4.1 git add--添加暂存区 4.2 git commit--提交本地仓库 4.3 git push--推送远程仓库 4.4 git pull--更新本地仓库 五、完整开发流程 5.1 步骤1:克隆项目 5.2 步骤2:创建自己开发…...
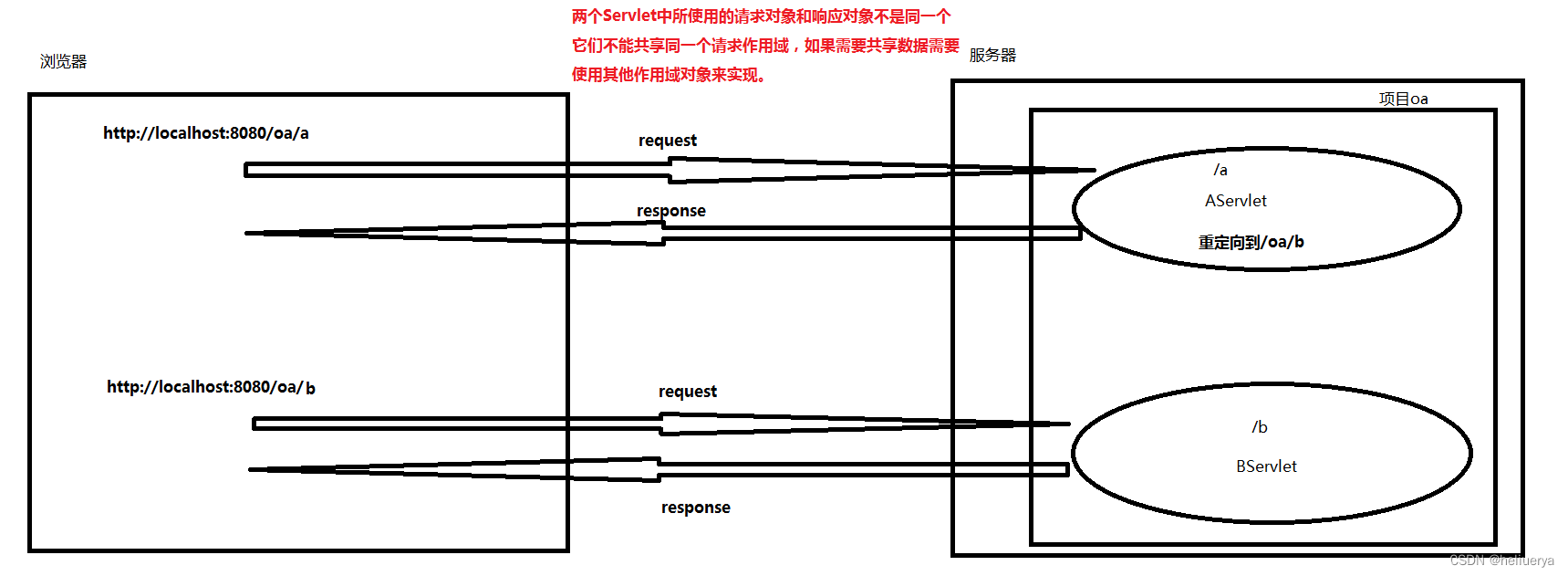
在一个web应用中应该如何完成资源的跳转
在一个web应用中通过两种方式,可以完成资源的跳转: 第一种方式:请求转发 第二种方式:重定向 转发和重定向的区别: 代码上的区别: 请求转发 // 获取请求转发器对象 RequestDispatcher dispatcher request.…...

前缀和部分题目
前缀和 前缀和指数组的前 N项之和,是个比较基础的算法 例题 面试题 17.05. 字母与数字 给定一个放有字母和数字的数组,找到最长的子数组,且包含的字母和数字的个数相同。 返回该子数组,若存在多个最长子数组,返回左…...
三天吃透MySQL面试八股文
本文已经收录到Github仓库,该仓库包含计算机基础、Java基础、多线程、JVM、数据库、Redis、Spring、Mybatis、SpringMVC、SpringBoot、分布式、微服务、设计模式、架构、校招社招分享等核心知识点,欢迎star~ Github地址:https://github.com/…...

Giving You A guide to learning any topic faster than 95% of people
A guide to learning any topic faster than 95% of people: Richard Feynman was a physician who won the Nobel Prize in 1965. But he became known for his great lectures. Why? He was able to explain complex concepts in simple terms with these 4 steps: 1 • E…...
大白话MySQL是如何根据成本优化选择执行计划的?(中))
(七十七)大白话MySQL是如何根据成本优化选择执行计划的?(中)
上次我们讲完了全表扫描的成本计算方法,相信大家应该都理解了,其实还是比较简单的,今天我们来讲一下索引的成本计算方法,因为除了全表扫描之外,还可能多个索引都可以使用,但是当然同时一般只能用一个索引&a…...

原来CSS 也可以节流啊
Ⅰ、前言 「节流」 是为了减少请求的触发频率,不让用户点的太快,达到节省资源的目的 ;通常 我们采用 JS 的 定时器 setTimeout ,来控制点击多少秒才能在触发;其实 通过 CSS 也能达到 「节流」 的目的,下面…...

UE官方教程笔记03-功能、术语、操作简介
对官方教程视频[官方培训]03-UE功能、术语、操作简介 | 徐良安 Epic的笔记这一部分基本都是走马观花的简单介绍功能世界创建建模Mesh editingtool是一个全新的建模工具,具备大多数的主流建模软件的核心功能HOUDINI ENGINE FOR UNREALHoudini编辑器,可以用…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...