如何理解泛型的编译期检查
既然说类型变量会在编译的时候擦除掉,那为什么我们往 ArrayList 创建的对象中添加整数会报错呢?不是说泛型变量String会在编译的时候变为Object类型吗?为什么不能存别的类型呢?既然类型擦除了,如何保证我们只能使用泛型变量限定的类型呢?
Java编译器是通过先检查代码中泛型的类型,然后在进行类型擦除,再进行编译。
例如:
public static void main(String[] args) { ArrayList<String> list = new ArrayList<String>(); list.add("123"); list.add(123);//编译错误
}在上面的程序中,使用add方法添加一个整型,在IDE中,直接会报错,说明这就是在编译之前的检查,因为如果是在编译之后检查,类型擦除后,原始类型为Object,是应该允许任意引用类型添加的。可实际上却不是这样的,这恰恰说明了关于泛型变量的使用,是会在编译之前检查的。
那么,这个类型检查是针对谁的呢?我们先看看参数化类型和原始类型的兼容。
以 ArrayList举例子,以前的写法:
ArrayList list = new ArrayList(); 现在的写法:
ArrayList<String> list = new ArrayList<String>();
如果是与以前的代码兼容,各种引用传值之间,必然会出现如下的情况:
ArrayList<String> list1 = new ArrayList(); //第一种 情况
ArrayList list2 = new ArrayList<String>(); //第二种 情况这样是没有错误的,不过会有个编译时警告。
不过在第一种情况,可以实现与完全使用泛型参数一样的效果,第二种则没有效果。
因为类型检查就是编译时完成的,new ArrayList()只是在内存中开辟了一个存储空间,可以存储任何类型对象,而真正涉及类型检查的是它的引用,因为我们是使用它引用list1来调用它的方法,比如说调用add方法,所以list1引用能完成泛型类型的检查。而引用list2没有使用泛型,所以不行。
举例子:
public class Test { public static void main(String[] args) { ArrayList<String> list1 = new ArrayList(); list1.add("1"); //编译通过 list1.add(1); //编译错误 String str1 = list1.get(0); //返回类型就是String ArrayList list2 = new ArrayList<String>(); list2.add("1"); //编译通过 list2.add(1); //编译通过 Object object = list2.get(0); //返回类型就是Object new ArrayList<String>().add("11"); //编译通过 new ArrayList<String>().add(22); //编译错误 String str2 = new ArrayList<String>().get(0); //返回类型就是String }
} 通过上面的例子,我们可以明白,类型检查就是针对引用的,谁是一个引用,用这个引用调用泛型方法,就会对这个引用调用的方法进行类型检测,而无关它真正引用的对象。
泛型中参数话类型为什么不考虑继承关系?
在Java中,像下面形式的引用传递是不允许的:
ArrayList<String> list1 = new ArrayList<Object>(); //编译错误
ArrayList<Object> list2 = new ArrayList<String>(); //编译错误我们先看第一种情况,将第一种情况拓展成下面的形式:
ArrayList<Object> list1 = new ArrayList<Object>();
list1.add(new Object());
list1.add(new Object());
ArrayList<String> list2 = list1; //编译错误 实际上,在第4行代码的时候,就会有编译错误。那么,我们先假设它编译没错。那么当我们使用list2引用用get()方法取值的时候,返回的都是String类型的对象(上面提到了,类型检测是根据引用来决定的),可是它里面实际上已经被我们存放了Object类型的对象,这样就会有ClassCastException了。所以为了避免这种极易出现的错误,Java不允许进行这样的引用传递。(这也是泛型出现的原因,就是为了解决类型转换的问题,我们不能违背它的初衷)。
再看第二种情况,将第二种情况拓展成下面的形式:
ArrayList<String> list1 = new ArrayList<String>();
list1.add(new String());
list1.add(new String());ArrayList<Object> list2 = list1; //编译错误没错,这样的情况比第一种情况好的多,最起码,在我们用list2取值的时候不会出现ClassCastException,因为是从String转换为Object。可是,这样做有什么意义呢,泛型出现的原因,就是为了解决类型转换的问题。
我们使用了泛型,到头来,还是要自己强转,违背了泛型设计的初衷。所以java不允许这么干。再说,你如果又用list2往里面add()新的对象,那么到时候取得时候,我怎么知道我取出来的到底是String类型的,还是Object类型的呢?
所以,要格外注意,泛型中的引用传递的问题。
相关文章:

如何理解泛型的编译期检查
既然说类型变量会在编译的时候擦除掉,那为什么我们往 ArrayList 创建的对象中添加整数会报错呢?不是说泛型变量String会在编译的时候变为Object类型吗?为什么不能存别的类型呢?既然类型擦除了,如何保证我们只能使用泛型…...
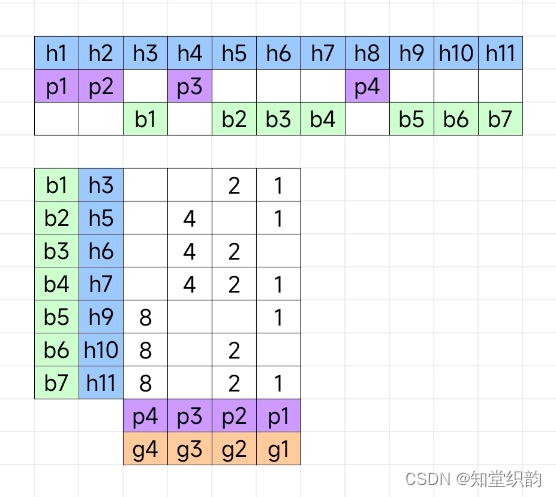
计算机组成原理:海明校验
在上图中,对绿色的7比特数据进行海明校验,需要添加紫色的4比特校验位,总共是蓝色的11比特。紫色的校验位pi分布于蓝色的hi的1, 2, 4, 8, 16, 32, 64位,是2i-1位。绿色的数据位bi分布于剩下的位。 在下图中,b1位于h3&a…...
信息学奥赛初赛天天练-39-CSP-J2021基础题-哈夫曼树、哈夫曼编码、贪心算法、满二叉树、完全二叉树、前中后缀表达式转换
PDF文档公众号回复关键字:20240629 2022 CSP-J 选择题 单项选择题(共15题,每题2分,共计30分:每题有且仅有一个正确选项) 5.对于入栈顺序为a,b,c,d,e的序列,下列( )不合法的出栈序列 A. a,b&a…...

第11章 规划过程组(收集需求)
第11章 规划过程组(一)11.3收集需求,在第三版教材第377~378页; 文字图片音频方式 第一个知识点:主要输出 1、需求跟踪矩阵 内容 业务需要、机会、目的和目标 项目目标 项目范围和 WBS 可…...

探索WebKit的守护神:深入Web安全策略
探索WebKit的守护神:深入Web安全策略 在数字化时代,网络已成为我们生活的一部分,而网页浏览器作为我们探索网络世界的窗口,其安全性至关重要。WebKit作为众多流行浏览器的内核,例如Safari,其安全性策略是保…...

unity ScrollRect裁剪ParticleSystem粒子
搜了下大概有这几种方法 通过模板缓存通过shader裁剪区域:案例一,案例二,案例三,三个案例都是类似的方法,需要在c#传入数据到shader通过插件 某乎上的模板缓存方法link,(没有登录看不到全文&a…...

凤仪亭 | 第7集 | 大丈夫生居天地之间,岂能郁郁久居人下 | 司徒一言,令我拨云见日,茅塞顿开 | 三国演义 | 逐鹿群雄
🙋大家好!我是毛毛张! 🌈个人首页: 神马都会亿点点的毛毛张 📌这篇博客分享的是《三国演义》文学剧本第Ⅰ部分《群雄逐鹿》的第7️⃣集《凤仪亭》的经典语句和文学剧本全集台词 文章目录 1.经典语句2.文学剧本台词 …...

React实战学习(一)_棋盘设计
需求: 左上侧:状态左下侧:棋盘,保证胜利就结束 和 下过来的不能在下右侧:“时光机”,保证可以回顾,索引 语法: 父子之间属性传递(props)子父组件传递(写法上&…...

【LeetCode】每日一题:三数之和
解题思路 最开始是打算沿着二数之和的思路做,即固定了最大的,然后小的开始遍历,因为这种遍历方式只需要遍历一轮就能完成,所以复杂度应该是O(n2),但是最后几个示例还是超时了,可能进…...

逆风而行:提升逆商,让困难成为你前进的动力
一、引言 生活,总是充满了未知与变数。有时,我们会遇到阳光明媚的日子,享受着宁静与和谐;但更多时候,我们却不得不面对那些突如其来的坏事件,如工作的挫折、人际关系的困扰、健康的挑战等。这些事件如同突…...

新能源汽车CAN总线故障定位与干扰排除的几个方法
CAN总线是目前最受欢迎的现场总线之一,在新能源车中有广泛应用。新能源车的CAN总线故障和隐患将影响驾驶体验甚至行车安全,如何进行CAN总线故障定位及干扰排除呢? 目前,国内机动车保有量已经突破三亿大关。由于大量的燃油车带来严峻的环境问题,因此全面禁售燃油车的日程在…...
【涵子来信】——社交宝典:克服你心中的内向,世界总有缺陷
内向,你是内向的吗?想必每个人不同,面对的情形也是不同的。 暑假是一个很好的机会,我是可以去多社交社交。但是,面对着CSDN上这么多技术人er,那么,我的宝典,对于大家,有…...

LabVIEW项目外协时选择公司与个人兼职的比较
在选择LabVIEW项目外协合作伙伴时,外协公司和个人兼职各有优劣。个人兼职成本较低且灵活,但在可靠性、技术覆盖面、资源和风险管理上存在不足。而外协公司拥有专业团队、丰富资源、完善的项目管理和风险控制,尽管成本较高,但能提…...

汽车电子工程师入门系列——CAN 规范系列通读
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 屏蔽力是信息过载时代一个人的特殊竞争力,任何消耗你的人和事,多看一眼都是你的不对。非必要不费力证明自己,无利益不试图说服别人,是精神上的节…...

泽众云真机-平台华为机型HarmonyOS NEXT系统已上线!
泽众云真机平台华为机型HarmonyOS NEXT系统已上线! 之前文章《泽众云真机-平台即将升级支持华为机型HarmonyOS NEXT系统泽众云真机-平台即将升级支持华为机型HarmonyOS NEXT系统》,为什么要升级HarmonyOS NEXT系统?我们之前有说过,…...

AI基础:从线性回归到梯度下降
一个简单的问题: 如果此时你正站在迷路缭绕的山坡上,能见度不高,但是你又想去往最低的山谷的位置,怎么走? 很简单,哪里陡那就往那里走呗——而这就是梯度下降算法的思想。 古话说:“先发制于人…...

AI产品经理面试
把优秀当习惯把优秀当习惯肯定不是口头说说,那有什么判断标准吗? 当我做完一件事儿的时候,我会看它有没有突破我的舒适圈、能不能惊艳到我自己。这就是我的判断标准。 在自我介绍和经历介绍时,面试者应该注重以下几个方面…...

二进制方式部署consul单机版
1.consul的下载 mkdir -p /root/consul/data && cd /root/consul wget https://releases.hashicorp.com/consul/1.18.0/consul_1.18.0_linux_amd64.zip unzip consul_1.18.0_linux_amd64.zip mv consul /usr/local/bin/ 2.配置文件 // 配置文件路径: /roo…...

SpringBoot整合Quartz实现动态定时任务
目录 1、Quartz简介1.1 Quartz的三大核心组件1.2 CronTrigger配置格式 2、SpringBoot整合Quartz框架2.1 创建项目2.2 实现定时任务 1、Quartz简介 Quartz是一个开源的任务调度服务,它可以独立使用,也可与其它的Java EE,Java SE应用整合使用。…...

qt 用宏控制静态接口的统一
1.概要 /** * 单件宏实验 * 创建一个可以生成单件的宏 * 起因:想让有些控件单件,但是c不支持静态的继承(c#支持) * 那么如果保证这些接口的统一呢,用宏 */ 2.代码 2.1 a.h #ifndef A_H #define A_H#include &…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
